一体化弹丸脱壳数值仿真研究

陈 亮，邱群先，何 行，刘可可

(中国船舶重工集团公司第七一三研究所，河南 郑州 450015)

一体化弹丸(Integration Launch Projectile,ILP)是近些年来随着电磁发射等技术的逐渐成熟而出现的一种新型弹药。与传统弹药相比，一体化弹丸在发射原理、弹药结构和外型上都有不同，但与脱壳穿甲弹(APFSDS)的脱壳机理类似。

一体化弹丸主要包括电枢、弹丸和弹托[1]，弹丸组件在轨道里运动的过程中，弹托对弹丸起保护功能，避免电流流入弹丸而造成弹丸内部的破坏，同时与电枢共同实现对弹丸的固定和运动导向。发射弹丸时，将组件放置于两轨道间初始位置，一体化弹丸以2～3 km/s的速度出炮口后[2]，电枢、弹托与弹丸受空气动力、重力等力的作用分开，弹丸飞向目标，完成打击目标的任务。电枢、弹托、弹体在飞散的过程中可能会出现碰撞的情况，影响弹体的飞行稳定性和射击精度，弹体速度快速衰减，降低了弹丸的射程。因此在一体化弹丸设计之初通过仿真计算研究得到相应的仿真数据为结构设计提供理论依据变得尤为重要。

就研究现状，从公开的资料来看，国内大多数的科研院所还是主要针对以电枢作为发射载体的研究，对一体化弹丸初始弹道脱壳的研究尚未开展。国外一体化弹丸的研究,美国走在了世界的前列，在2015年海军科技博览会上展出了BAE公司研制的32 MJ炮口动能的情况[3]，并公布了其在达尔格伦试验场一体化弹丸脱壳试验视频。

目前尚无公开文献对一体化弹丸脱壳流场进行类似的仿真研究，考虑到一体化弹丸与APFSDS在结构上类似，脱壳原理存在着相似性，传统的脱壳动力学可用于一体化弹丸脱壳原理的分析。黄振贵等运用Fluent对尾翼稳定脱壳穿甲弹脱壳动力学的过程进行了三维数值模拟，分析了APFSDS在不同时刻下初始分离过程激波的转换过程，仿真结果显示弹托和卡瓣的瞬时飞散状态，同实验得出的分离轨迹图较为吻合，表明CFD对APSFDS超高速扰流的动态分析具有较强的数值模拟能力[4]。Guillotine等基于外弹道方程数值计算了多种IAT弹托分离的弹道轨迹，与采用实验、分析模型得到的弹道吻合较好[5]。张学伟等基于CFD动网格技术和外弹道六自由度方程，研究了在不同攻角下对尾翼稳定脱壳穿甲弹脱壳过程的影响,仿真结果表明脱壳弹在正负攻角飞行时，弹托分离时间增加，不利于弹托的分离[6]。武频等应用有限体积TVD格式数值模拟了APFSDS弹托分离干扰的三维流场，仿真结果表明弹托和弹体之间存在较强激波反射交汇，并同实验结果有较好的吻合[7]。

笔者针对一体化弹丸结构，建立了脱壳模型，结合流体动力学和外弹道学理论，对一体化弹丸脱壳过程进行了动态仿真，获得了脱壳过程中弹托、弹丸的运动轨迹以及相关的动态参数，该仿真结果为一体化弹丸结构设计提供了重要的理论依据。

1 仿真计算方法

1.1 仿真思路

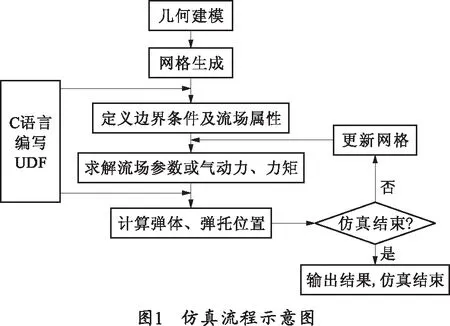
一体化弹丸流场脱壳仿真即求解瞬态气体流场的参数分布以及流场中求解弹体、弹托六自由度空间运动姿态，故主要涉及到流场的求解、6DOF 刚体运动解算，同时由于弹体、弹托等相对于空间变化而引起的网格更新。具体的仿真思路为：在求解开始时通过UDF输入弹体、弹托等刚体的质量、转动惯量等物理参数，通过求解非定常欧拉流体控制方程，得到此时刻分离过程的流场分布情况；然后沿着弹体和弹托表面对压力进行积分求得弹体、弹托所受的气动力和绕心力矩。将此求解的动力学参数代入6DOF 刚体运动方程，解算出下一时刻弹体、弹托的空间位置和运动学参数；最后由动网格技术中的弹簧光顺法和局部网格重构法根据新的边界值自动计算出弹体、弹托移动后网格节点位置。通过不断的迭代重复计算即整个分离过程进行数值模拟；同时在整个仿真过程中通过设置某些时间点保存求解过程中的数据；并在后处理中再现整个分离过程。流场与6DOF刚体运动方程的耦合求解全过程如图1所示。

1.2 动力学方程

流体参数计算采用N-S粘性非定常流动控制方程[8]：

(1)

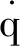
(2)

式中：γ为理想气体绝热指数；p为气体压强，由理想气体状态方程p=ρRT确定，R为普适气体常数；T为气体温度。

上述方程组不封闭，要对其进行求解，一种方法是推导出雷诺应力等关联项的输运方程，即雷诺应力模型；另一种方法则是引入湍流模型进行求解，考虑到一体化弹丸在无限空气场中运动，认为流动完全是湍流，忽略空气分子的粘性影响，采用标准k-ε模型，其方程形式如下：

式中：Gk表示由于平均速度梯度引起的湍动能产生；Gb表示由于浮力影响引起的湍动能产生；YM为可压速湍流脉动膨胀对总耗散率的影响；μ为湍流粘性系数，

(4)

求解封闭的流体控制方程，采用有限差分的方式离散求解，空间上采用有限体积法(FVM)，为提高计算精度，采用二阶迎风格式。6DOF运动方程用于描述弹体、弹托刚体在空间作六自由度运动时运动参数变化，分为动力学和运动学方程，质心运动标量形式的动力学方程为

刚体绕质心转动标量形式的动力学方程为

(6)

质心运动的运动学方程为

(7)

刚体绕质心转动的运动学方程为

(8)

随着时间的推移，六自由度方程不断地求解弹体、弹托的位置，计算空间域中出现网格拉伸或压缩，甚至发生畸变而出现计算中止的情况。为保证计算的顺利必须采用动网格技术更新网格以适应计算域的变化，采用弹簧光顺法和局部重构法对网格进行重新离散更新。

2 模型建立与设置

一体化弹丸连接零件较多，弹托、电枢等结构较为复杂，如果在模型建立时将其全部考虑在内，对整个模型的网格划分造成很大的困难，事实上这些附属部件对弹丸、弹托的分离流场影响较小。为了网格离散化和计算方便，在建模时去除一体化弹丸的电枢、卡销、弹簧等部件，经过简化后得到由四瓣托包裹弹丸的模型，如图2所示，同时忽略上下弹托、左右弹托在结构质量外形上由于加工等因素的不一致性，在建立模型时完全按对称来处理，并留出弹托、弹体之间3 mm的空隙以便于后期网格的划分建立和动网格区域更新。

外流场选择在8 970 mm×2 400 mm×2 400 mm的长方体空气域内。整个计算区域采用四面体非结构化网格进行划分。考虑到一体化弹丸脱壳时周围气动参数变化较大，为提高仿真精度，对其表面及附近区域进行了高密度的网格划分。远离一体化弹丸的区域网格划分较为稀疏，最终得到整个模型的网格数为300万左右。

计算区域采用弹簧光顺法和局部重构法来更新动网格，并编写UDF设定弹托、弹体的质量和转动惯量，选择6DOF来计算弹托弹体在脱壳过程中不同位置的运动参数。将坐标系选择在弹托对称的中心位置，并设定弹托、弹体的质心坐标以及其初始速度v0=2 000 m/s；设定远场边界条件为压力出口，压力值为一个标准大气压；计算时为更加接近实际，将重力以及真实地平面空气参数考虑在内，脱壳初始状态攻角为0°.由于马赫数较高，对流动方程的计算离散方法上时间采用基于隐式向后时间差分格式，空间上采用基于有限体积法,选用迎风格式中二阶隐式AUSM格式，加速收敛并克服在高马赫数下Roe格式出现的红宝石现象。

3 结果分析讨论

进行非定常计算，前期采用时间步长0.1 μs,后期加快计算速度改为0.12 μs，计算11 000步左右结束后可见弹托、弹体完全分离。

3.1 分离流场结果与分析

为方便分析以z=0剖面(图2中弹托1、弹托2和弹体的共有对称面)显示作图观察。图3为不同时刻x-y平面上分离过程的压力云图以及相对位置。

在初始分离阶段t=0.05 ms时刻，弹头体部和弹托前缘的激波开始形成并迅速耦合，前腔和前端部的球形域内形成了高压区，该高压区作用在上下弹托的前半部分开始相对于弹体径向分离，但初期分离的距离较短，高压气体还不足沿着小缝隙在极短时间由弹前流向弹尾部，在缝隙内导致拥塞的出现，压力沿着缝隙线性分布。弹尾部气流高速流动，使得尾部出现负压区域，气流出缝隙后绕着两侧弹托尾部流走而出现对称的涡流区。

在t=0.20 ms时刻前腔及前端部的球形区域基本完成泄压，弹前后激波完全形成并开始耦合。弹托由于角运动内表面开始成为迎风面，上表面由于成为背风面而形成了低压区。弹托与弹体开始分离使得弹托上下沿生成脱体激波，上下压差激波给弹托提供很大的翻转力矩，弹体由于上下左右压力的对称性而抵消，可以沿着平直的轨道继续前行。

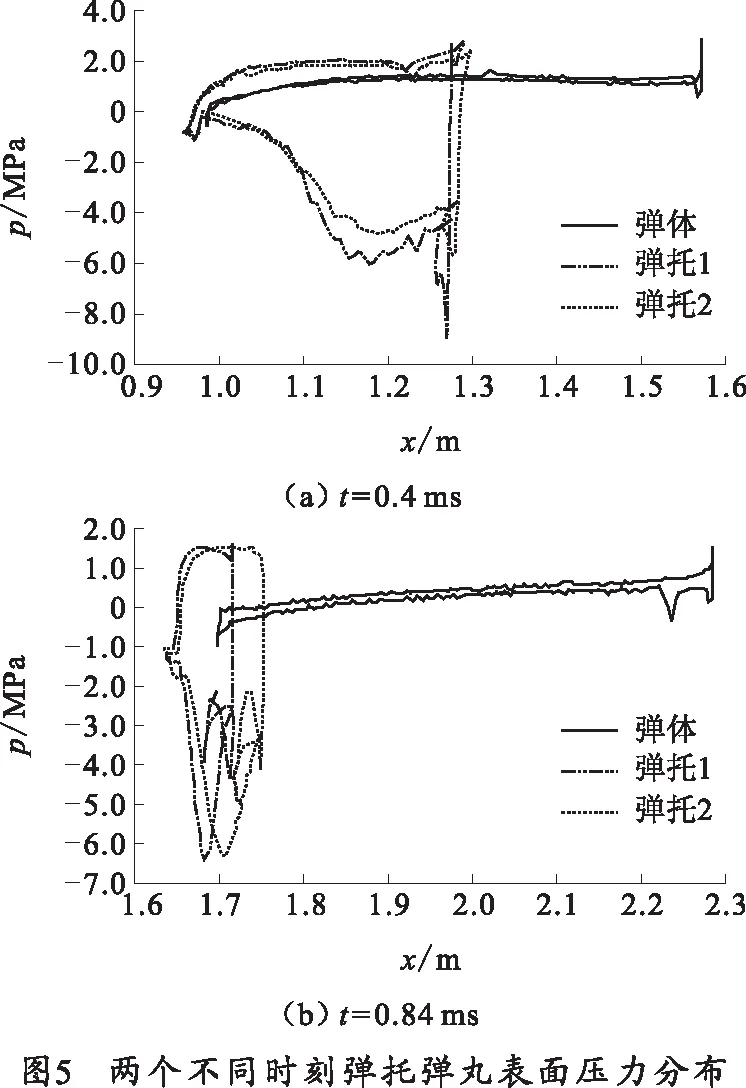
在t=0.40 ms时刻弹体开始完全进入弹托、弹体头部的强激波耦合区，此时弹托产生的高压区对弹体的飞行稳定性干扰最大,弹托前沿压力达到峰值，如图4所示，约为4.3 MPa，之后迅速下降。弹托压力面上的压差达到峰值，如图5(a)所示，到t=0.84 ms时弹托内侧面完全垂直迎风状态，整个内面受压均匀，如图5(b)中所示，弹体表面压力值由于激波区耦合作用的减弱而降低，说明此时激波耦合基本结束，开始进入分离阶段。弹托后沿低压区压力达到最大值，之后基本属于稳定状态，如图6所示。

在t=0.96 ms时刻弹托、弹体流场耦合结束，弹托倾角大于90°，激波分离完成。到t=1.24 ms时刻弹托、弹体流场基本分离结束，但仍然存在局部反射的弱余波存在于弹体上部和弹尾部下方，如图3(f)所示分别形成了高压区(316～780 MPa)和低压区(-1080～-148 MPa)，使得弹体表面受到非对称压力，形成绕心的不平衡力矩，影响弹丸的飞行稳定性。

3.2 弹托6DOF运动结果与分析

同样以z=0剖面(图2中弹托1、弹托2和弹体的共有对称面)作为分析的平面，图7为分离结束时速度矢量图，显示了一体化弹丸脱壳结束时刻的弹托、弹体的位置，图中3条白色部分是动网格追随弹体或弹托运动轨迹更新，代表着弹体弹托的运动轨迹，可以看出弹托相对于弹体分别向两侧斜上方散开，呈弧形轨迹。

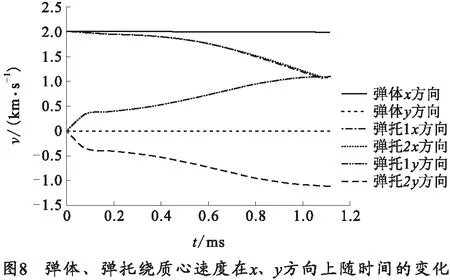
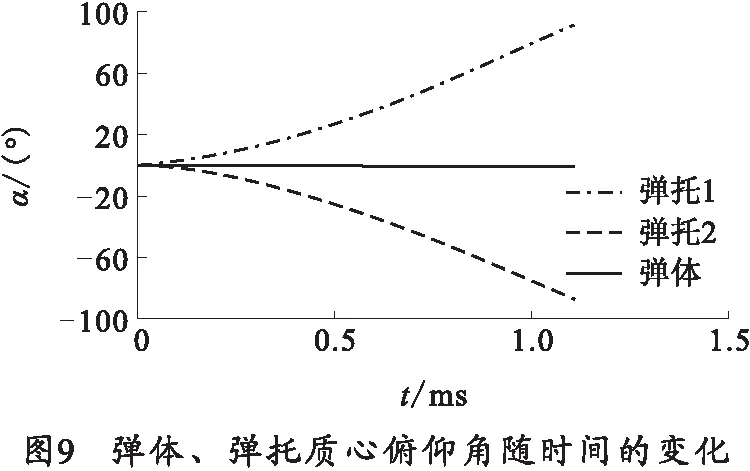
弹体、弹托绕质心速度在x、y方向上随时间变化如图8所示，在图中显示上下弹托轴向(x方向)速度衰减逐渐加快，这是由于俯仰运动过程中的过程中俯/仰角变大，如图9所示，使得轴向方向上迎风面逐渐增大，整个受到轴向阻力加大，减速增快。在径向方向上表现出：先匀速增大然后加速变陡最后缓慢上升，即y方向力先恒定后增加最后减小。说明弹托前后沿压差随着弹托、弹体激波流场的耦合和分离呈现复杂的变化趋势。

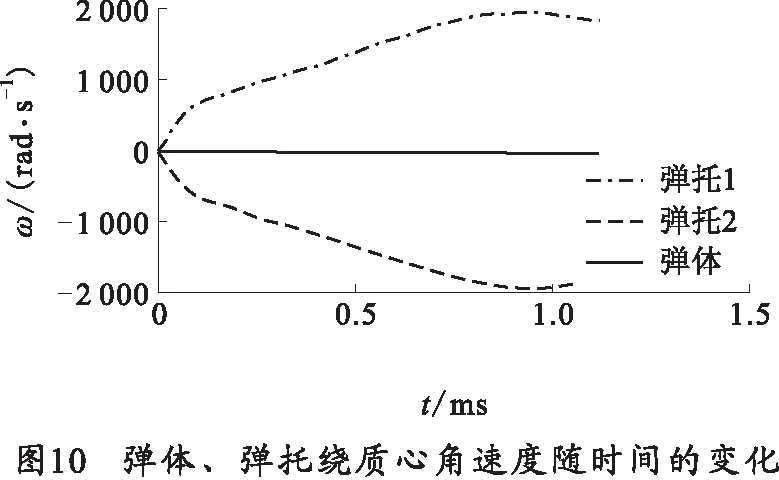
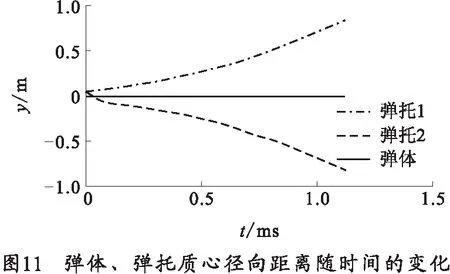
总体上质心轴向位移逐渐变缓，径向位移逐渐加快。绕质心角速度由于力矩大小的复杂变化而在不同阶段表现不同增长速率，如图10所示。上下弹托运动的径向距离呈现对称状态，如图11所示，说明重力在整个脱壳过程中影响很小。

4 结论

笔者基于UDF，采用动网格技术和刚体6DOF运动方程，通过Fluent软件对一体化弹丸膛口脱壳流场非定常状态进行了仿真研究。直观地反映出脱壳过程中弹托、弹丸流场耦合作用下连续脱壳过程中流场分布情况，得到分离流畅压力分布，弹托、弹体运动等相关数据。

1)整个脱壳过程中弹体、弹托各自飞行产生的激波大致可分为3个阶段：激波生成阶段(0～0.2 ms)、激波耦合阶段(0.2～0.84 ms)、激波分离阶段(0.84～0.96 ms).在激波耦合段虽然弹体受到弹托激波流场的强烈干扰，但由于整体流场的对称性而相互抵消，重力影响有限，弹体不偏离预定飞行轨迹。整个脱壳时间1.24 ms,仿真结束后显示弹体末速度为1 979.7 m/s，损失率为1.015%.

2)分离后期(t=1.24 ms)，弹托激波反射在弹体上的弱余波仍然存在，并在弹体头部上方和弹尾部下方分别形成局部高压区和局部低压区，该区域可能使弹体产生不平衡力矩而出现“栽头”现象。