复杂曲面误差评估的最小区域包容配准算法
谭高山,张丽艳,刘胜兰
(1.安徽工业大学 数理科学与工程学院,安徽 马鞍山 243032;2.南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
误差源于制造不精确,其对零件的装配质量和使用性能有重要影响,因此评估制造工件是否满足设计误差要求是生产制造中必不可少的环节。评估复杂零部件误差时,首先利用测量设备获得零部件的测量模型,然后对齐测量模型与设计模型,确定零部件是否符合设计要求[1]。最小区域法是符合形位误差定义和误差评定相关标准规定[2]的对齐方法。对于规则几何特征,无论评估方法还是检测设备均已成熟,但包含自由曲面的复杂零部件的误差评估仍然很困难。为了简便易行,工程中仍然使用多种近似方法[3-7]进行误差评估,包括目前市场上的商业软件,近似方法在评估精度要求较高的复杂曲面时,会因过高的估计误差而导致复杂零部件误报废[4]。测量点的代数拟合方法在数值上往往不稳定,测量点的微小扰动都可能导致拟合参数明显改变,造成评估结果不可靠。几何拟合又称为配准或定位,即通过确定一个三维刚体变换来统一或对齐测量坐标系和设计坐标系[8],不同配准方法往往会导致不同的评估结果。
工业上通常用几何公差(GD/T)标准[9]来评估制造工件与其设计要求的一致性。“包含几何特征的公差带定义了几何特征的形位公差”,即测量数据必须位于理论模型的两个包容面内,包容面间的距离反映了几何特征的误差大小。ISO标准[10]规定了误差评估的最小区域准则。极值是轮廓度误差评估中应用最广的一个参数,从这个角度说,最小区域准则在直观上是最恰当的评估准则,该准则通过定位包含测量模型的两个等距面来获得最小轮廓度误差。
另一常用评估准则是极大极小准则,目标是最小化最大绝对误差[11-13],这种评估优化模型求解困难,尤其是测量数据较多时效率较低。实际上,当几何模型对称时,极大极小准则与最小区域准则等价,特殊情况下可用极大极小准则代替最小区域准则获得最小区域误差。然而情况并不总是如此,第1章对此进行举例说明。
求解最小区域误差的算法较多[14-19],如计算几何法、直接搜索法、向量法、支持向量机法和暴风算法(Brute Force,BF)等,这些方法利用了待评估曲面的特殊几何性质。直接搜索法不但效率较低,而且存在收敛问题;计算几何法要求计算测量模型的最近和最远Voronoi图,为了提高计算精度,需要花费较长的计算时间。另外一些简单几何特征的最小区域配准还可通过解析法实现[20]。以上利用曲面特殊几何性质的评估方法不适用于复杂曲面误差评估问题。启发式智能优化算法[21-25]也是求解最小区域配准的常用算法,如免疫进化算法、拟粒子群算法、微分进化算法、蚁群算法和人工蜂群算法等,然而这些算法非常敏感,且一般效率较低。
本文给出一种基于最小区域准则的复杂曲面误差评估配准模型,并研究这一复杂问题的高效求解方法。从数学上来说,该配准模型最小化了理论曲面两个等距面之间的距离,两个等距面包含了待评估模型的所有测量数据。由于目标函数是极值函数,在算法上找到目标函数的一致光滑逼近是高效求解配准模型的关键。本文利用凝聚函数的思想将非光滑配准模型转化为无约束可微优化问题,并采用低存储拟牛顿算法进行高效求解。
首先分析复杂曲面最小轮廓度误差评估的配准问题并进行建模,通过仿真说明模型不但满足最小轮廓度误差定义和曲面评估的最小区域准则,而且对曲面的几何性质没有特殊要求。然后研究了模型的高效求解问题,最后通过仿真示例和实测模型验证了本文算法的适应性和优势。
1 问题分析与数学建模
设测量数据集为P={Pi|i=1,2,…,n},设计模型为Q。最小区域配准的目的是找到合适的三维刚体变换,使得理论模型包含所有测量数据的两个等距面之间的距离最小。测量模型相对理论模型的偏差可通过式(1)定义的有向距离函数表示:
di(R,T)=(RPi+T-Qi)·ni。
(1)
式中Pi(i=1,…,n)为测量点,Qi是Pi在理论模型上的对应点,ni为Qi处的曲面外法向量;R∈3×3和T∈3分别为三维刚体变换的旋转矩阵和平移向量。本文以经典的迭代最近点(Iterative Closest Point, ICP)算法的配准结果作为初始位姿,通过k-d树搜索算法寻找测量点Pi(i=1,…,n)在理论模型上的最近点,用最近点代替测量点的对应点。配准目的是使对应点对之间的几何关系满足具体工程要求。显然,有向距离的正负分别表示测量点位于理论模型两侧。误差评估要求测量模型相对理论模型的偏差越小越好,因此建立配准模型

(2)
式中I={1,2,…,n},n为测量数据点的个数,复杂曲面测量模型的数据量往往较大。
模型(2)基于最小区域准则,满足ISO/TS 和 ANSI 标准。实际上目标函数是偏差向量函数D(X)=(d1(X),d2(X),…,dn(X))的一种新的度量,本文称为极差范数,模型(2)优化的新范数最小。
为更清楚地描述问题,设空间向量为X=[θx,θy,θz,tx,ty,tz],则偏差函数转化为X的多元函数
di(X)=(R(X)Pi+T(X)-Qi)·ni,
(3)
从而将式(2)转化为式(4),即以X为优化变量的误差向量函数的极差范数最小化问题。
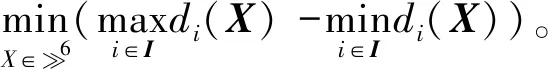
(4)
下面通过模拟多边形配准说明模型(4)对最小区域评估的适用性。图1所示为不同准则下的模拟配准,其中离散点为取样点,实线表示理论多边形,虚线表示不同配准结果的误差区域。图1a所示为ICP结果,图1b所示为极大极小准则下的配准结果,图1c所示为本文所提最小区域的配准的结果,这3种方法分别优化了理论模型和测量数据之间的欧氏距离误差向量的2-范数、1-范数和有向距离误差向量的极差范数。由图可知,所提方法的轮廓度误差最小,即获得了最小误差带。对于一些简单几何特征,最小区域配准结果的最优性和唯一性已经得到证明[2]。实际上,考虑计算的复杂性和数据模型的特殊性,常见一些文献用极大极小配准模型来实现最小区域配准,这一数学模型优化了两数据模型之间的最大欧氏距离。例如对一些简单几何特征,以及一些具有对称性或非封闭的曲面进行极大极小配准和所提最小区域配准时,最小轮廓度误差一致,但是情况并不总是如此。图1示例对此进行了说明,分析发现有向距离误差向量的极差范数是最小区域误差的最佳度量,因此式(4)是具有明确最小区域的配准模型,其对待配准曲面的几何性质没有特殊要求,适合高精度的复杂曲面评估。
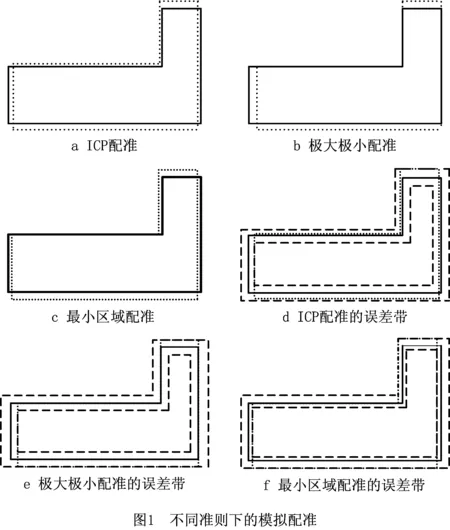
以上分析说明式(4)所示配准模型是曲面最小区域评估的合理表示,这一优化模型的目标函数非光滑,由于非光滑函数下降方向的搜索比光滑函数困难得多,下面着重解决这一问题。
2 凝聚函数逼近及优化求解
非光滑优化问题一般采用直接搜索法或启发式搜索算法求解,相对传统的微分类优化算法,这些搜索算法的效率和精度往往不够理想,有时甚至无法保证收敛性。熵正则化方法[26-27]利用凝聚函数一致光滑逼近非光滑函数,凝聚函数是带有控制参数的显式可微函数。本文利用凝聚函数,分别考虑最小值、最大值函数的一致光滑逼近,最小值函数等价于
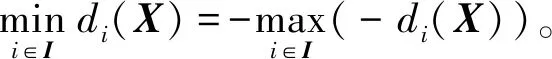
(5)
因此将式(4)转化为
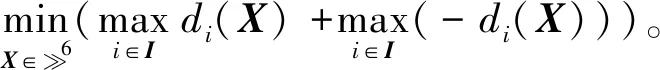
(6)
需要强调的是,式(6)是式(4)的另一种表达形式。因为di(X)及其相反函数的最优值并不能保证同时达到,所以式(6)与极大极小问题的本质不同。
参照笔者以前的工作[28],推导得式(6)目标函数的二阶可微凝聚函数近似Fp(X),
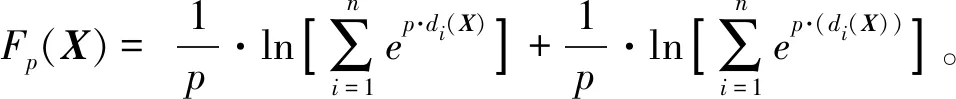
(7)
式中控制参数p在理论上趋向正无穷大。因此式(4)转化为如下无约束优化问题:

(8)
BFGS(Broyden-Fletcher-Goldfarb-Shanno) 算法是求解这类问题最常用的典型拟牛顿算法,仅需计算函数值和梯度值。
记di(X)(i=1,…,n)及其相反函数在第k次迭代时的函数值D+(X(k))和D-(X(k)):
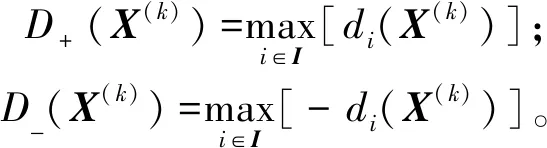
(9)
为方便表示,采用式(10)表示相关点的下标集合:
E+(X(k))={i|di(X(k))=D+(X(k)),i∈I};
E-(X(k))={i|-di(X(k))=D-(X(k)),i∈I};
O+(X(k))={i|p·(D+(X(k))-
O-(X(k))={i|p·(D-(X(k))-

(10)
式中L为数值计算中数据溢出的临界值。函数值和梯度值分别表示为:
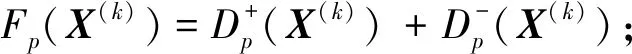
(11)
(12)
式中:
ui(X(k))=
vi(X(k))=

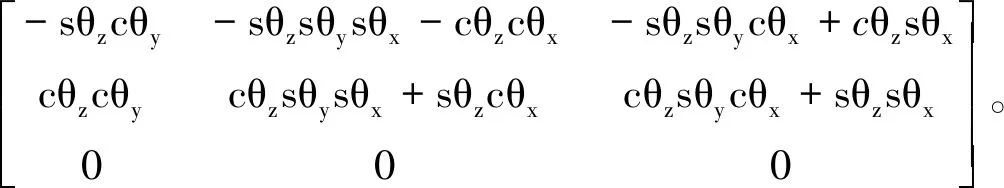
为解决数据溢出问题,采用L-BFGS 算法求解式(8),该算法较BFGS算法具有更高的数据存储能力。考虑参数p对配准精度、效率、数值稳定性和收敛性的影响,下一章验证算法对参数的敏感性,由实验知参数p可在一个较大的范围内进行有效取值。
3 实验
为验证算法性能,本章比较经典的ICP配准、序列二次规划方法求解的极大极小配准和本文用L-BFGS算法求解的最小区域配准的结果。实验在2.10 GHz的CPU 和2.5 GB的RAM个人机上采用VC++编程实现。为公平起见,不同方法的数据结构、最近点的搜索、有向距离的计算等其他方面都采用相同的处理方法。
3.1 仿真数据实验
为更清楚地比较所提最小区域配准法与极大极小配准法的区别与联系,本节以平面为例进行实验。具体为在商业软件中模拟生成平面,通过随机扰动获得平面测量模型的118个采样点,并经微小刚体变换作为初始状态,ICP算法配准获得的轮廓度误差为4.90 mm,本文算法下降到4.52 mm,相对ICP配准结果,本文配准结果更优。极大极小配准轮廓度误差也是4.52 mm,这与前文分析一致,即对于一些特殊几何特征(如对称几何特征),极大极小配准和本文最小区域包容配准所得的最小轮廓误差相同。3种方法的误差分布情况如表1所示,可见极大极小方法中的总体平均误差、正向平均误差和负向平均误差均大于本文方法,显然没有一种方法可以获得比本文方法更小的轮廓度误差,这是因为本文方法直接优化了表示轮廓度误差的极差参数。ICP法直接优化最小均方根误差,因此获得了3种方法中最小的均方根误差。
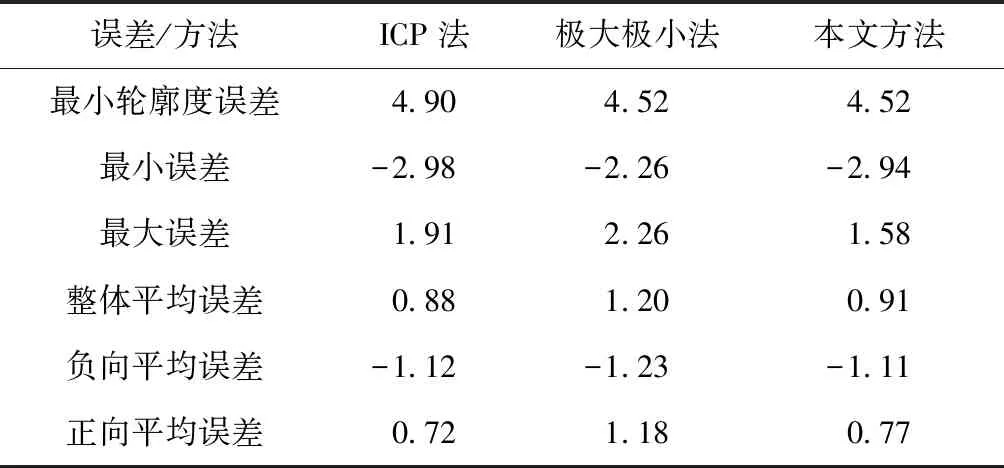
表1 仿真平面配准评估结果 mm
3.2 实测钣金件误差评估实验
本文实验研究某实测液压成型钣金件的误差评估配准问题,该钣金件由包括自由曲面在内的复杂曲面构成,变形导致钣金件的误差分布难以估计,因此装配前在算法上对齐测量模型与其理论模型具有重要意义。首先利用流行商业软件Imageware® 中的“best fit”功能获得初始位姿,然后采用ICP方法和本文方法分别进行配准。图2所示为所提方法的配准结果,可见误差分布相对集中,最小轮廓度误差为1.74 mm,而ICP算法为1.83 mm。对于高精度要求的钣金零件评估来说,精度的微小改善都具有重要意义。表2所示为不同方法的误差统计结果,可见无论正向还是负向,本文方法的最大误差都更小,而且本文方法的正向均方根误差0.21 mm也比ICP算法的0.23 mm小,但是两种方法的负向误差分布大体一致。为更清楚地反映不同算法的误差分布,对不同误差区间的样本数据个数进行统计。ICP算法和本文方法在误差区间(-0.5, 1.5)内的数据点数分别为74.56%和70.18%,验证了基于最小二乘准则的ICP算法的误差分布在整体上更均衡。实际上,误差评估的最小区域准则是要获得最小的轮廓度误差,常用的最小二乘准则虽然获得了误差均衡,但是并不能保证轮廓度误差最小,若将误差区间缩小为(-0.5, 0.5),则两种方法对应的数据点数分别为35.96%和35.08%,比较接近,因此本文方法不但满足了误差评估的最小区域准则,而且高精度区域的误差分布也比较均衡。

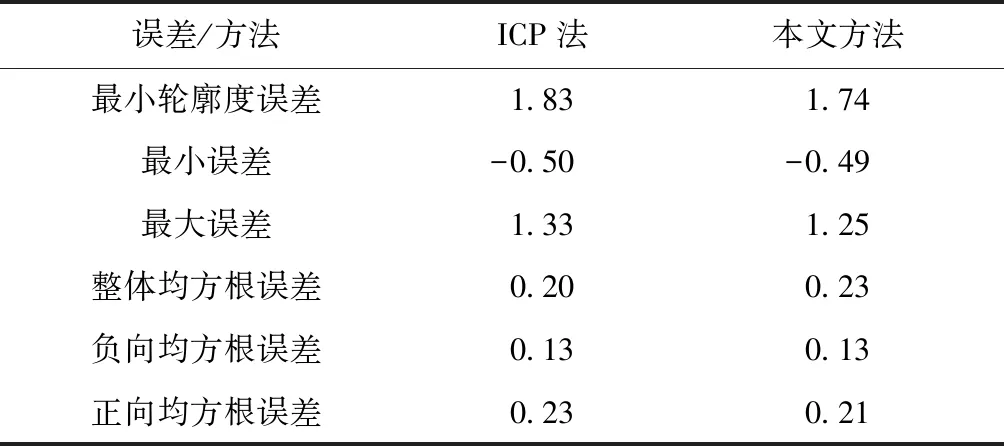
表2 实测钣金件的配准评估比较mm
4 结束语
本文提出一种面向复杂曲面误差评估的最小区域包容配准方法,通过建立具有明确物理意义的极差配准模型,并利用经典拟牛顿法求解配准模型的一致光滑无约束逼近问题,实现了复杂曲面的最小轮廓度误差评估。通过模拟仿真数据和实测钣金件的误差评估实验说明所提算法有助于减少生产中由于过高估计误差引起的误报废问题,从而验证了算法的适用性和优势。

