基于改进灰狼优化算法的自动化立体仓库作业能量优化调度
刘恺文,曹政才
(北京化工大学 信息科学与技术学院,北京 100029)
0 引言
仓库作为制造企业中一个重要的组成部分,准确快速的仓库管理技术保证了企业在市场中的竞争力[1-2]。作为一种新型仓储技术,自动化立体仓库因其空间利用率高、作业高效及节约劳动力而得到科研人员和企业管理者的广泛关注[3]。随着自动化和智能化技术的发展,自动化立体仓库正朝着大型化、智能化和精细化管理的方向发展,企业对自动化立体仓库的需求也变得更加复杂和多样,因此面临着更多的挑战。
对于一个已确定相关配置的自动化立体仓库,出入库作业效率的高低主要取决于调度算法的优劣,其直接影响物流企业的运营成本。因此,作为其中的关键技术,自动化立体仓库的调度问题受到了国内外学者的广泛关注,并取得了很多成果。Ma等[4]提出一种融合集成学习思想的多目标生物地理学优化算法,并成功将其运用于求解自动化立体仓库作业调度问题;Kung等[5]以多堆垛机共享分拣巷道为主要研究问题,建立了自动化立体仓库调度动态规划模型,并采用一种快速顺序调度方法进行求解,提高了堆垛机的分拣效率;Gharehgozli等[6]提出一种多项式时间算法来解决自动化仓库中的堆垛机总行程时间最小化问题,获得了较好的结果;Chen等[7]考虑自动化立体仓库订单任务货位分配问题,采用一种改进禁忌搜索算法解决中大问题规模情况下的货位分配问题,并通过仿真实验验证了所提算法的有效性;颜波等[8]考虑自动化立体仓库中通常以订单为调度整体,整合考虑其中出库和入库任务,建立了以最大完工时间和最大订单拖期为目标的调度优化模型,并采用一种帝国竞争算法进行求解。
由上述可知,大多数学者在研究自动化立体仓库调度问题时,通常仅考虑出入库货物的货位分配问题、最小化任务的最大完工时间或堆垛机分拣路径优化等问题。另外,大多数研究在对调度问题建模时,对所涉及作业的操作设备往往仅考虑一种固定的设备配置,与实际自动化立体仓库调度问题存在一定偏差。2014年国务院印发的《物流业发展中中长期规划(2014~2020年)》对物流企业明确提出了节能减排、绿色环保要求,以及目前逐渐实施的峰谷分时电价策略,使得自动化立体仓库调度过程中的设备能耗问题成为不可忽视的一个重要因素。因此,研究自动化立体仓库中的设备能耗最优,无论从经济角度还是环保角度,都具有重要的理论意义及实践价值。
本文针对某自动化立体仓库调度流程,研究自动化立体仓库中出入库作业调度问题,针对出入库作业操作最大完工时间与堆垛机能耗之间的关系构建相应的惩罚函数,并将其应用于改进的灰狼优化(modified Grey Wolf Optimization, mGWO)算法,实现带有截止时间约束的自动化立体仓库堆垛机能耗调度优化算法。灰狼优化(Grey Wolf Optimization, GWO)算法是2014年提出的一种新型群体智能算法,该算法通过模拟灰狼种群中的社会阶级和狩猎觅食场景构建算法的搜索框架,已经在路径规划、参数优化等方面获得了应用[9]。因为传统的GWO算法在求解组合优化问题过程中容易出现陷入局部最优的情况,所以在原有算法框架下引入Lévy飞行策略和多种群重组策略来改善算法的寻优能力和搜索深度。
1 问题描述
在自动化立体仓库的出入库作业调度流程中,堆垛机分拣模式通常分成模式单指令作业模式和复合作业模式两种。当巷道堆垛机运行在单指令作业模式下时,一趟行程中最多只能完成一个出库任务或一个入库任务,这种堆垛机作业模式效率低下,不具有可调度性;当堆垛机运行在复合作业模式下时,根据堆垛机所配备的载具数量,一趟行程可以同时完成两个或者多个任务,并且可以通过设置合理的任务执行次序减少堆垛机的作业时间,提高自动化立体仓库的执行效率。因此,本文主要研究复合作业模式下带有截止时间约束的单一载具堆垛机作业能量优化问题。
1.1 最近邻策略
入库货物的货位分配策略分为定位存储和随机存储两种,不同的存储策略有不同的优点,因此在本文的出入库作业调度问题中考虑两种货位存储策略。
对于随机存储策略,本文采用一种最近邻策略对入库货物进行货位分配,通常通过计算巷道堆垛机从IO位置到各个可选货位的行程时间来评价可选货位之间的优劣,其计算方式为
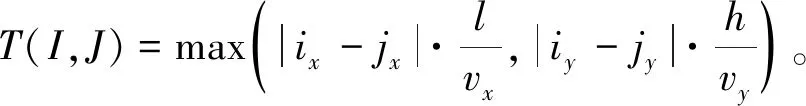
(1)
式中:T(I,J)表示巷道堆垛机从货位I到货位J的行程时间;I(ix,iy)和J(jx,jy)分别表示货架上对应的位置;vx和vy分别表示堆垛机在水平方向和垂直方向上的速度;l和h分别表示货位的相应尺寸。
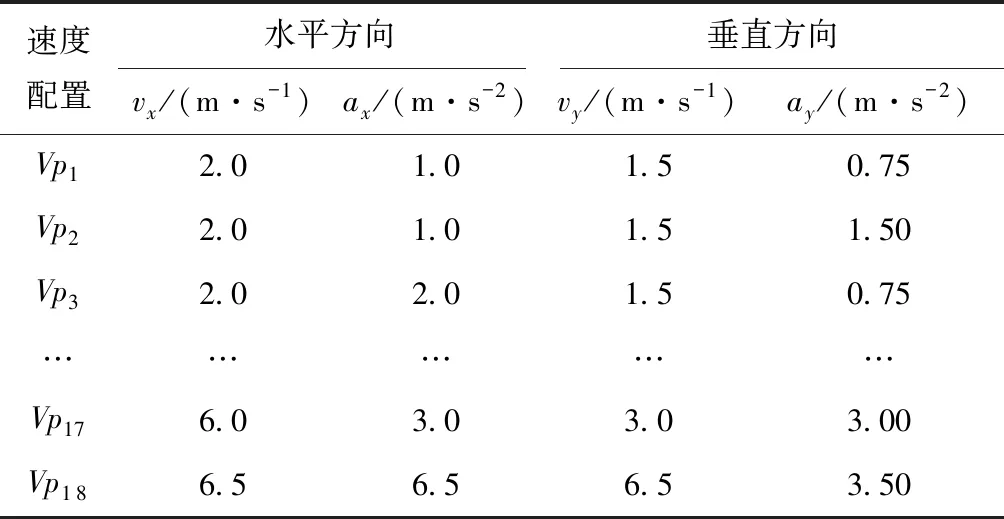
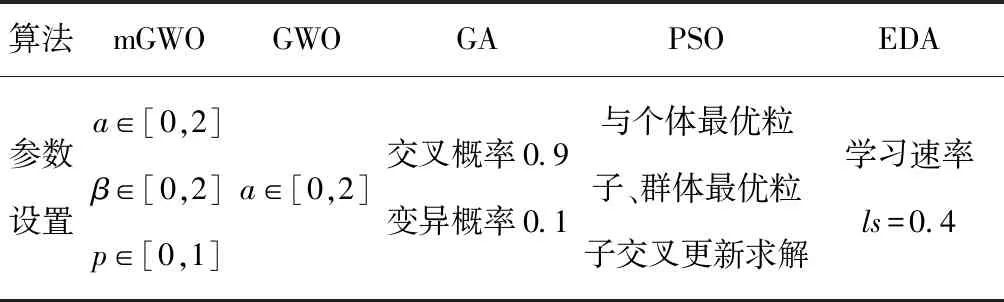
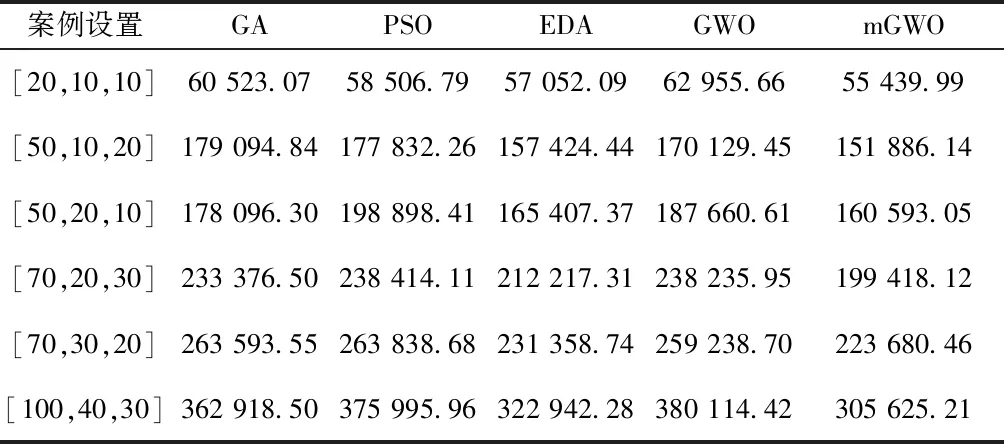
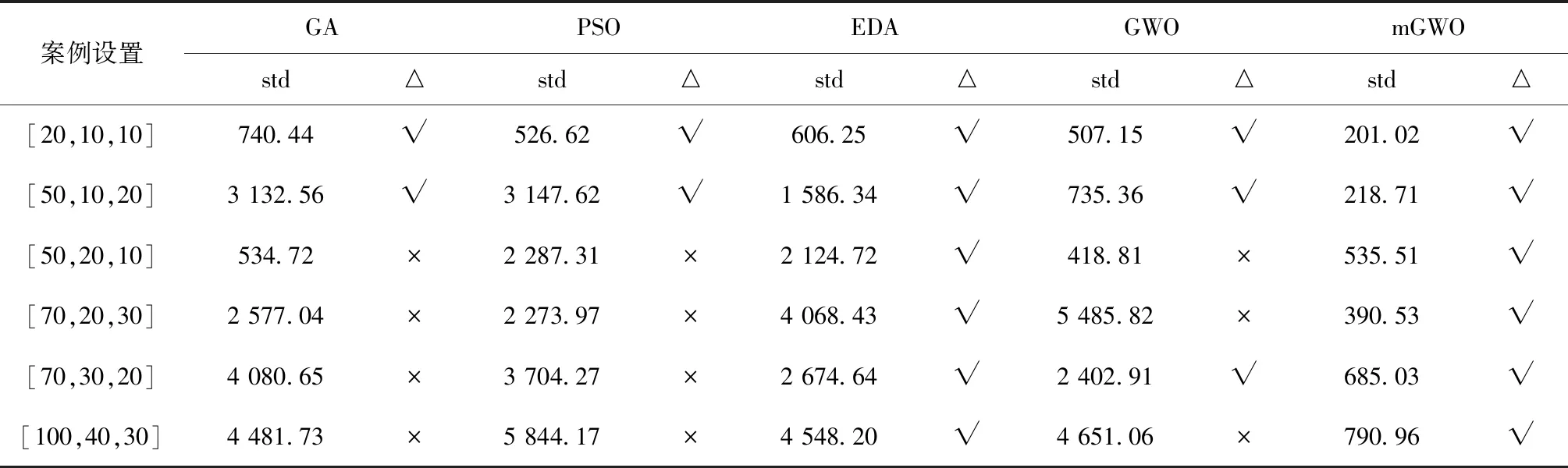
如图1所示的简化例子,对于候选货位P1和P2,若TOP1 巷道堆垛机水平方向和垂直方向的运动相互独立,因此运行状态下所需的能量为水平方向运动所消耗的能量和垂直方向运动所消耗的能量Ey[10],即 Etotal=Ex+Ey。 (2) 通过分析巷道堆垛机在作业过程中的受力平衡关系,可计算其作业功率大小,然而堆垛机在不同运行状态下的功率计算方法也不同,具体描述如下: (1)匀速状态下的功率描述 水平方向为 (3) 式中:MTv为匀速运动下的驱动扭矩;r为行走轮半径;η为电机能量转化效率;kr为滚动阻力系数;G表示重力。 垂直方向为 (4) (2)非匀速状态下的功率描述 水平方向为 (5) 式中:MTa为加速运动下的驱动扭矩;kir为非匀速状态下的转动质量阻力系数;a为堆垛机加速度;g为重力加速度。 垂直方向为 (6) 设Tin={1,2,3…,n}为待出库任务集合,Tout={1,2,3,…,m}为待入库任务集合,每个作业任务最多需要一趟行程即可完成。本文的自动化立体仓库巷道堆垛机仅配备一个载具,因此当堆垛机运行在复合作业模式下时,任务次序必须为先执行入库作业任务后执行出库作业任务。 为了更好地描述一辆巷道堆垛机运行在复合作业模式下的调度过程,建立如下数学模型: (7) s.t.Tdd-Cmax≥0; (8) ∑vi,m,t=1,∀i∈Tin∪Tout; (9) vi,j,m+vj,i,m≤0.5·(ui,m+uj,m); (10) vi,j,m+vj,i,m≥ui,m+uj,m-1; (11) Si,m,l≥Cj,m,l,i∈Tout,j∈Tin。 (12) 其中:i为出入库作业任务集合;m为设备标号,文中仅考虑一台堆垛机,因此m=1;Tdd为该批任务的截止时间;Cmax为该批任务的最大完工时间;l∈max{Tin,Tout}为堆垛机行程索引;Si,m,l为第i个任务由堆垛机m执行的开始时间,Cj,m,l为任务j由堆垛机m执行的完成时间;决策量vi,j,m=1表示任务i在任务j完成之后由堆垛机m执行,反之则相反;决策量ui,m=1表示任务i由堆垛机m执行,反之则相反。 在上述数学模型中,式(7)中的F为目标函数,表示执行完全部出入库任务后堆垛机所消耗的能量之和,其中Eix和Eiy分别表示堆垛机执行任务i时在水平方向和垂直方向上消耗的能量,具体计算方法如1.2节所述;式(8)表示任务的截止时间约束;式(7)和式(8)表明了该出入库作业调度的目标为在满足满足截止时间约束的同时,要使堆垛机的能效最优;式(9)表示在同一时刻同一辆堆垛机最多只能运输一个货品;式(10)和式(11)表示同一辆堆垛机上执行的任务之间有先后次序;式(12)表示同一趟行程中出入库任务之间具有先后次序关系。 上述模型存在截止时间约束,即整个自动化立体仓库能量调度问题中出入库作业时间Cmax要在截止时间Tdd之前完成。因此,为了在所设定的可行域中找到最优解,同时考虑到堆垛机能耗F与最大完工时间Cmax之间带有数量级差距,通过设置合理的惩罚函数对搜索得到的不可行解进行惩罚,使搜索过程收敛到可行域内,以保证最后所得解的可行性。对此,构建增广目标函数 (13) 式中:σ为惩罚因子;F为能耗计算方法。 为了使算法能够快速收敛到可行解区域,惩罚因子根据不可行解占种群比例大小的变化而改变,即 (14) 式中λamp为惩罚因子放大系数。 在算法迭代过程中,解的分布存在两种情况:①所有解均不在可行解区域内;②存在解分布在可行解区域内。为了能够更好地比较两种情况下解之间的优劣,将对应的增广函数值定义为 (15) 本节采用mGWO算法求解带有截止时间约束的自动化立体仓库出入库作业能量优化问题。该算法主要基于GWO算法的基本框架,由于传统GWO算法在求解该组合优化问题中效果不佳,引入带有Lévy飞行的个体更新策略及改进种群重组策略来提高算法的寻优能力,算法整体流程图如图2所示。 GWO算法模拟自然界灰狼种群中的社会等级机制和捕食行为,将整个灰狼种群分为Alpha,Beta,Delta,Omega 4个层级,其中Alpha,Beta,Delta为种群中最好的3个候选解,其余个体被分到Omega层级。算法分为围捕操作和个体更新操作,各操作具体描述如下: 灰狼种群的包围捕食行为可以描述为 D=|C·Xp(t)-X(t)|; X(t+1)=Xp(t)-A·D; (16) A=2a·r1-a;C=2·r2。 (17) 式中:t为当前的迭代次数;A和C为协同系数向量;Xp和X为当前猎物和灰狼个体的位置向量;参数a随迭代过程从2线性递减到0;r1和r2为[0,1]中的随机数向量。 狼群中Omega层级个体的位置通过种群中Alpha,Beta,Delta的位置进行引导更新,更新策略为: Dα=|C1·Xα-X|;X1=Xα-A1·Dα; (18) Dβ=|C2·Xβ-X|;X2=Xβ-A2·Dβ; (19) Dδ=|C3·Xδ-X|;X3=Xδ-A1·Dδ; (20) (21) 式中:参数A决定GWO算法的全局搜索和局部搜索,|A|>1时算法进行全局搜索,|A|<1时算法进行局部搜索;参数C控制猎物与灰狼之间的距离。 本文的调度方案包括出入库任务执行次序、入库任务分配和堆垛机速度配置等多种信息,因此采用三段式混合编码方式对个体进行编码。在自动化立体仓库运行过程中,出入库任务的数量一般不同,因此仅考虑出库任务数量多于入库任务数量的情况。将每个个体编码成一个3×D维矩阵,其中D表示堆垛机的总行程数。图3所示为个体编码方式的一个实例,图中出库作业数为5,入库作业数为3,堆垛机速度配置数为4,每一列表示堆垛机的一趟行程。 图3中,前两段采用自然数编码方式对出入库任务的执行次序以及堆垛机一趟行程中的入库任务进行分配,第三段采用整数编码表示该趟行程中堆垛机所选择的速度配置编号。因为出入库任务数量不同,而编码方式采用等长的编码段,所以需要一个修复算子g对个体编码进行修正: (22) 式中(m,n)表示出库任务数为m、入库任务数为n的实例。对于图3描述的实例,入库任务对应编码从[2,4,1,5,3]修正为[2,0,1,0,3],其中入库任务次序编码位为0表示在对应堆垛机行程中仅有一个出库任务。 传统GWO算法在求解此类组合优化问题时存在陷入局部最优的问题,因此在个体位置更新中引入Lévy飞行策略,用于协助GWO算法跳出局部最优进行全局搜索[11]。作为一种非高斯随机化的过程,该策略的随机飞行步长服从Lévy稳定分布,使得搜索算法个体能够搜索到目标空间中的不同区域。Lévy分布的简化形式为 (23) 对此,将灰狼个体的更新操作改为 (25) 该更新策略通过控制量|A|控制个体位置更新模式,如式(24)所示。当|A|>0.5时,通过采用带有Lévy飞行的策略来更新个体位置,否则采用经典GWO算法的个体位置更新策略进行位置更新。 作为一类复杂组合优化问题,本文所研究的自动化立体仓库调度问题直接通过式(25)的位置更新策略进行个体位置更新会产生大量不可行解(生成解的编码不符合算法设定的编码方式),因此要对生成个体X(t+1)的位置进行修正。因为本文采用自然数编码方式,所以采用随机键编码的LOV(largest order value)规则,将按各编码位值排序后各编码位在排序序列中对应的位置信息作为个体转换后的编码。假设存在3个体X1=[5,3,4,1,2],X2=[4,3,2,1,5],X3=[1,2,5,3,4],当采用GWO算法更新策略X(t+1)=(X1+X2+X3)/3时,得到X(t+1)=[3.33,2.67,3.67,1.67,3.67],通过排序获得其位置信息为X(t+1)=[4,2,1,3,5],即满足算法个体的编码[12],采用Lévy飞行策略的个体位置更新也采用该方法进行转换。 为了提高mGWO算法的搜索效率,快速搜索到可行域中较优的个体,在原有算法框架中引入一个多种群重组策略。令原灰狼种群为Popold,经过2.3节位置更新后的种群为Pop。为了增加下次迭代过程中初始种群的优势个体数量,引入一个扰动种群Popmutate,该种群的生成方式参考变邻域搜索算法中的邻域扰动方式,通过随机选择当前迭代过程中Alpha,Beta,Delta中的一个个体进行扰动操作生成Popmutate,具体的扰动策略如图4所示。 图4中x(t)和x(t+1)为个体编码中的一段自然数编码,p为随机向量,随机选择p中[i,i+len]之间的序列,将其随机打乱,在原x(t)中,更换扰动前后p(i,i+len)序列对应的个体编码向量所对应的位置,使整个编码向量中最多只有len个位置发生变化,从而保证个体编码的稳态更新。例如,图4中i=2,len=3,选择个体的编码位置为[2,1,5],随机打乱后为[1,5,2],交换x(t)中对应的位置得到[2,5,1,3,4]。对于个体编码的速度配置选择部分,通过随机选择两个位置j,k,并对选择的j,k进行随机变异可以得到扰动后的速度配置。执行popsize次上述操作可以获得扰动后的种群Popmutate。 对Popold,Pop,Popmutate进行重组形成allpop,计算allpop的增广目标函数值,选择其中增广目标函数值较低的popsize个体组成Popnew进入下一次迭代过程。 为了验证所提mGWO在求解带有截止时间约束的自动化立体仓库能量优化调度问题的性能,本文根据所研究的自动化立体仓库货架物理尺寸随机生成多种问题规模进行数值仿真。 某自动化立体仓库货架的物理尺寸为长30 m、高6 m,货位宽高分别为0.5 m和0.3 m,库区空间平均使用率为70%~80%,巷道堆垛机可选的速度配置参数部分数据[10]如表1所示。 表1 巷道堆垛机部分可选速度配置 为了验证算法的性能,根据仓库的布局大小随机生成多种问题规模。为了描述简便,将测试案例定义为元组[m,n,u],其中m为出库任务数量,n为定位存储任务数量,u为随机存储入库任务数量。 将案例规模分别设置为元组[50,20,10],[50,10,20],[70,30,20],[70,30,20],[70,20,30],[100,40,30],括号中的3个数据分别为出库任务数量、定位存储任务数量、随机存储入库任务数量。对比算法为经典GWO算法、遗传算法(Genetic Algorithm,GA)、粒子群优化(Particle Swarm Optimization,PSO)算法和分布估计算法(Estimation of Distribution Algorithm, EDA)等,各比较算法的参数如表2所示。 表2 算法参数设置 所有数值仿真实验均在同一条件下进行(种群大小和迭代次数相同),每个案例独立运行5次,计算得到的设备能耗平均值、标准差和截止时间的约束满足情况等如表3和表4所示。 表3 mGWO与其他比较算法在不同问题规模的能耗平均值比较 表4 mGWO与其他比较算法在不同问题规模的能耗标准差及截止时间约束符合程度比较 注:△表示仿真案例是否在截止时间Tdd之前完工,std为多次运行结果的标准差;√表示满足截至时间约束,×表示不满足。 为了解决自动化立体仓库出入库作业调度过程中的堆垛机能量优化问题,本文根据实际自动化立体仓库调度流程,同时考虑定位存储和随机存储两种入库任务的存储策略以满足不同情况,并对随机存储任务采用一种最近邻策略进行货位选择来降低搜索范围。针对整个出入库作业调度流程,建立了一个带有截止时间约束的自动化立体仓库出入库作业调度能量优化模型,通过引入惩罚函数改善调度方案对截止时间约束的符合程度。本文采用一种mGWO算法对问题进行求解,该算法针对传统GWO算法在解决离散类优化问题时存在搜索能力不足以及容易陷入局部最优的问题,引入结合Lévy飞行的个体位置更新策略,该策略中服从Lévy分布的随机步长设置使算法能够搜索到目标空间的不同区域,帮助算法跳出局部最优;同时引入一个种群重组策略,通过多种群融合重组有效提高了算法的收敛能力和局部搜索能力。最后通过数值仿真实验并与已有算法进行比较表明,所提算法在求解自动化立体仓库出入库作业调度问题上可行并具有良好的性能。 本文采用所提算法求解自动化立体仓库出入库作业调度问题所得的解,给仓库决策者从出入库作业次序、任务行程分配和堆垛机速度配置设定几个方面提供了完备的调度方案,进而在满足实际截止时间约束的同时降低仓库的运营成本,具有重要的实践价值。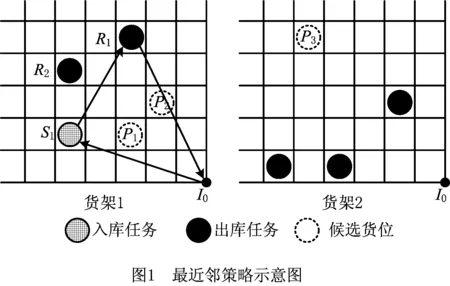
1.2 堆垛机能耗模型

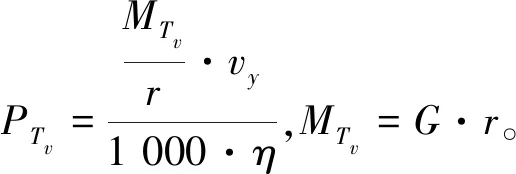

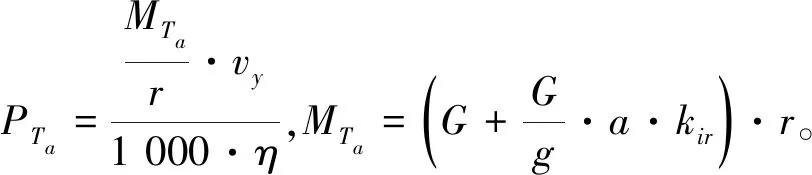
1.3 数学模型


2 改进灰狼优化算法
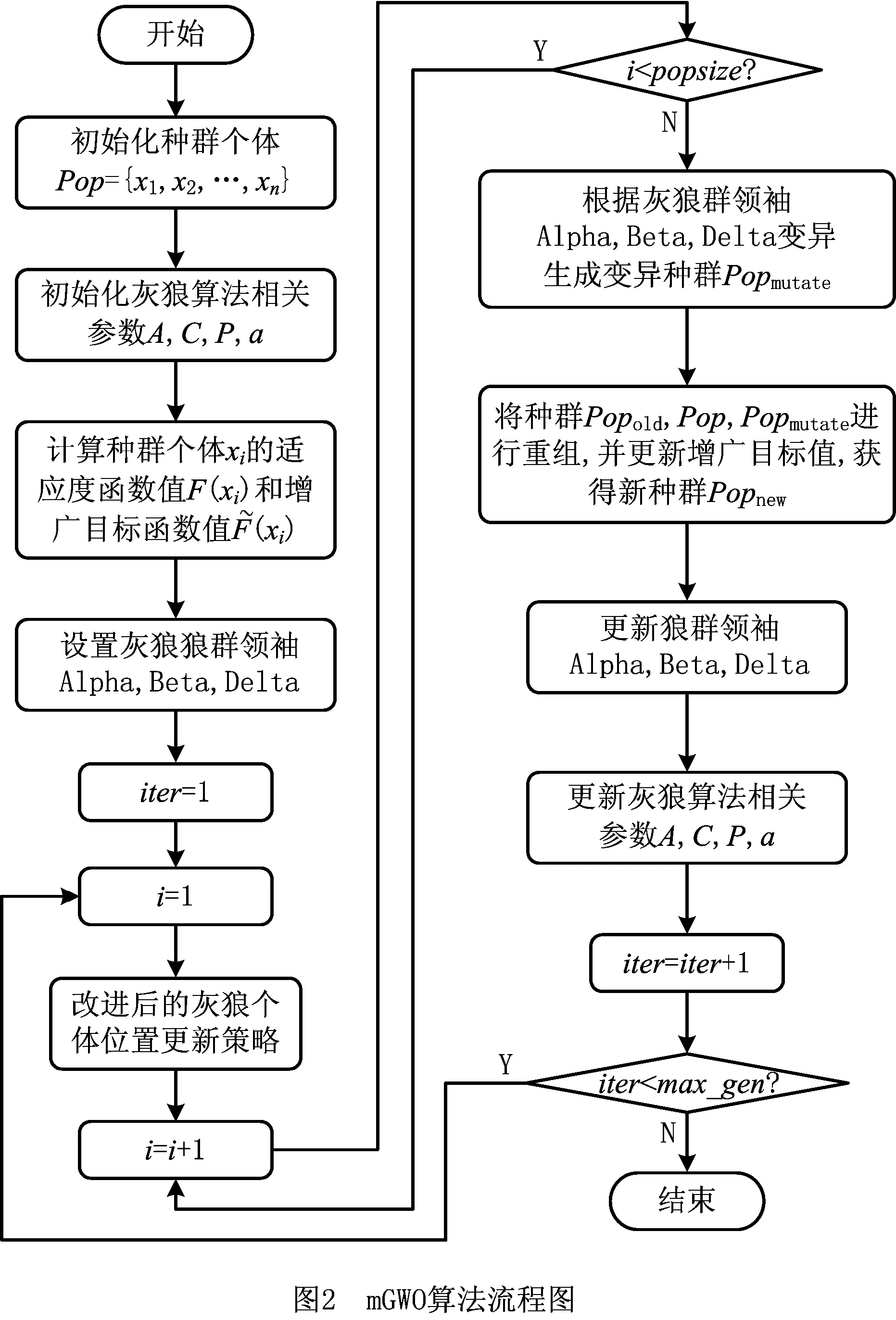
2.1 传统灰狼优化算法

2.2 编码与解码

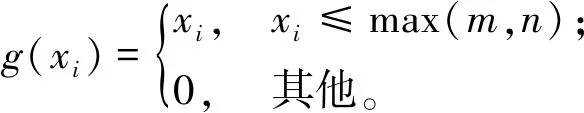
2.3 融合Lévy飞行的个体位置更新策略


2.4 多种群重组策略

3 仿真实验
3.1 参数设置
3.2 结果与分析

4 结束语

