基于分数阶PID算法的磁流变液柔顺关节控制研究
余建军,蔡世波,胥 芳,韦 威,鲍官军,张立彬
(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310014)
0 引言
近年来,协作型机器人在工业装配、生活服务、医疗手术等领域得到了日益广泛的应用[1-2]。在与人体交互作业的过程中,协作机器人不仅要有较高的位置和力/力矩控制精确性,还要有足够的作业安全性,传统协作型机器人是基于刚性传动部件进行关节传动,基于多模传感信息融合及复杂控制算法达到控制精确性与作业安全性的目标[3]。研究人员不断尝试研究开发具有可变刚度特性的柔顺关节,并将其与传统刚性关节型机械臂集成应用,以期通过更便捷的感知与控制方法获得系统的柔顺性与安全性[4]。
磁流变液是一种主要由载液、软磁材料颗粒、表面活性剂组成的智能材料,具有可控流变特性,当外磁场强度为零时表现为牛顿流体,当施加外磁场时表现为黏塑性体,且其黏性随外磁场强度的变化而变化[5-6]。Takesue等[7-8]基于磁流变液的可控流变特性设计出一种高扭矩、低惯性的磁流变离合器,并提出一种提高磁流变离合器扭矩响应特性的反馈控制方法;Miura等[9]基于磁流变液的流变特性提出一种用于被动控制的驱动器,实验研究表明这种驱动器有外力作用时才会产生阻力,适用于人机交互的场景;Wang等[10]设计了一种高扭矩—重量比的磁流变离合器,在此基础上开展了扭矩开环控制实验和碰撞安全性实验,实验研究表明,磁流变离合器的阶跃响应特性优于摩擦离合器;Kim等[11]基于磁流变液制动器进行了闭环耐久性控制实验研究,实验结果表明,磁流变液制动器在剪切模式下工作105次循环后仍然具有很好的闭环控制效果;Li等[12]设计了一种磁流变离合器,基于Bingham模型提出一种(剪切应力和励磁电流的)拟合模型,基于常规比例—积分—微分(Proportional-Integral-Derivative,PID)控制策略实现了磁流变离合器的扭矩输出控制。目前,研究人员对磁流变液传动装置的研究多集中于离合器、制动器和阻尼器,将磁流变液传动装置应用于机器人关节的研究较少。
本文提出一种基于磁流变液耦合传动的机器人柔顺关节,该关节主要由伺服电机、减速机、柔顺关节耦合器组成,其中柔顺关节耦合器即为基于磁流变液设计的一种多片式耦合传动装置,利用磁流变液的可控流变特性可使机器人关节具有主动柔顺特性和更高的安全性。同时提出基于分数阶PID(PIλDμ)的磁流变液柔顺关节耦合器扭矩控制方法[13],并开展了磁流变液柔顺关节耦合器扭矩控制实验。
1 基于磁流变液的机器人柔顺关节
1.1 柔顺关节结构
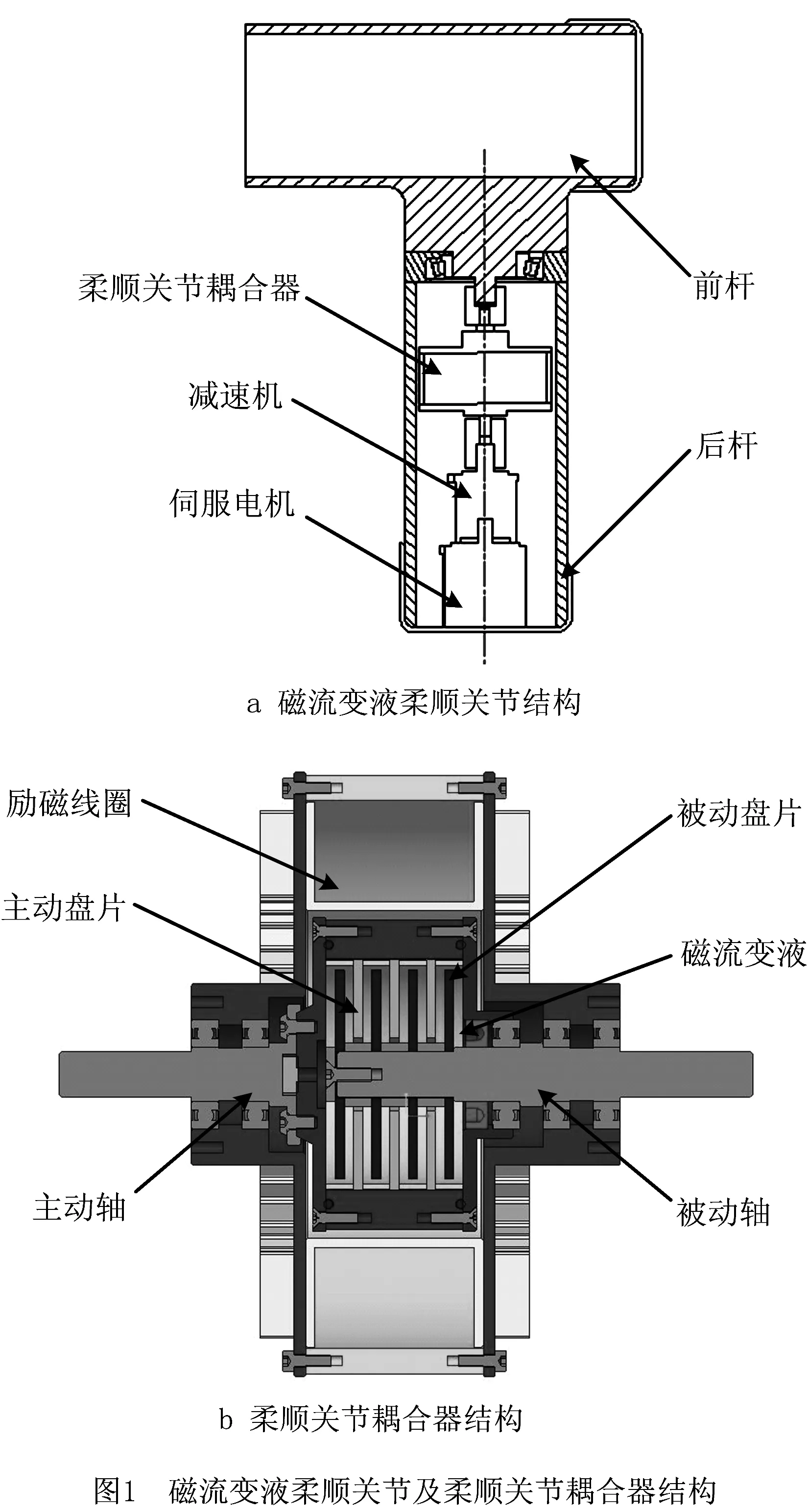
基于磁流变液的机器人柔顺关节主要由前杆和后杆组成,其中后杆内部安装有伺服电机、减速机和柔顺关节耦合器,其结构示意图如图1 a 所示。柔顺关节耦合器是磁流变液柔顺关节的核心传动部件,其结构如图1 b所示,磁流变液填充于柔顺关节耦合器主、从动盘之间的工作间隙,在外部磁场作用下呈现可控的剪切屈服应力,从而能够在主、被动盘片之间发挥力矩传递的作用。当励磁电流发生变化时,磁流变液会发生流变效应,且其流变过程可控、可逆。当励磁电流为零时,磁流变液会转化为牛顿流体;当励磁电流足够大时,磁流变液会转化为类似固态的黏塑性体,宏观表现为磁流变液的黏性可调,进而能够传递可控扭矩。基于磁流变液的机器人柔顺关节即利用了磁流变液的可控流变特性,使前杆的扭矩输出具有主动柔顺性,由于磁流变液剪切屈服应力的可控特性,使磁流变液柔顺关节前杆在运动过程中具有更高的安全性。表1所示为柔顺关节耦合器的相关设计参数。

表1 柔顺关节耦合器设计参数
1.2 柔顺关节耦合器静态模型
磁流变液填充于柔顺关节耦合器主、被动盘片之间的工作间隙,在零磁场条件下呈现为牛顿流体,此时主要依靠磁流变液自身的零场粘度发挥扭矩传递作用,剪切应力与剪应变率呈线性关系。逐渐增大励磁电流时,外磁场强度随之增大,磁流变液的宏观表现为粘度增大。剪切应力受磁场强度和剪应变率的影响,根据Bingham-Plastic模型[14],磁流变液剪切传动过程的剪切应力
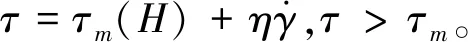
(1)
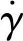
(2)
式中:Δω为(柔顺关节耦合器)主、被动盘片之间的速度差;r为磁流变液的工作半径;h为磁流变液的工作间隙。式(1)中的第二项是由磁流变液自身黏度产生的扭矩,可以忽略不计。
根据以上分析,在柔顺关节耦合器的传动盘片工作界面半径r处取一微圆环,宽度为dr,得到的微传递扭矩
dT=τ·2πr·rdr。
(3)
因为柔顺关节耦合器有多个盘片,设柔顺关节耦合器的主动盘片和被动盘片的工作间隙数量为N,所以对式(3)两边进行积分可得柔顺关节耦合器的输出扭矩
(4)
式中R1和R2分别为柔顺关节耦合器被动盘片的外圆半径和主动盘片的内圆半径。
励磁线圈通电后,在外部磁场作用下将磁性颗粒链看作均匀的板,采用Maxwell应力张量理论,考虑颗粒磁饱和与磁场集中效应[15],得到磁流变液静态屈服应力为
τm(H)=H2μ(χ⊥+1)sinθcosθ。
(5)
式中:μ为真空磁导率;χ⊥为垂直于板的磁化率;θ为磁场与板的夹角。
根据文献[16],磁场强度H和磁感应强度B的关系为
B(H)=C1eC2H+C3。
(6)
基于柔顺关节耦合器的磁路分析,结合安培定律得到磁感应强度B和励磁电流I的关系为

(7)
式中:Rm为柔顺关节耦合器的磁路总磁阻;S为导线截面积;n为励磁线圈匝数。联立式(5)~式(7),代入式(4)可得柔顺关节耦合器扭矩传递静态模型为
(8)
式中:C1,C2,C3均为常量,通过试验测试得到;μ,χ⊥,θ根据实验数据,用MATLAB工具箱System Identification Toolbox辨识得到。
1.3 柔顺关节耦合器扭矩传递动态模型
基于Bingham-Plastic的模型可以在静态过程中准确建立柔性关节耦合器输出扭矩与电流的静态关系式,但是无法计算动态过程中柔顺关节耦合器的实际输出扭矩。这是因为Bingham-Plastic模型本身忽略了磁流变液以外的其他因素,磁流变液的磁滞现象不明显,而且响应时间为毫秒级,与磁流变液相比,柔顺关节耦合器中其他导磁部件存在的磁滞和漏磁现象会导致柔顺关节耦合器的动态响应无法像静态模型那样准确。另一方面,磁流变液在滑差传动过程中的温漂特性、流体之间的摩擦都会影响柔顺关节耦合器的动态性能,也增加了控制难度。考虑上述因素,现有理论难以建立精确的柔顺关节耦合器动态模型,本文采用自回归原理[17],将模型的下一个输出样本与之前的观察结果相关联,即
y(t)=-a1y(t-1)-…-any(t-n)
+b1μ(t-1)+…+bmμ(t-m)。
(9)
式中:y(t-i)和μ(t-i)(i=1,2,…)分别为t时刻之前输入量和输出量的观测值;ai,bi(i=1,2,…)为模型参数。
根据式(9)可以得到柔顺关节耦合器输出扭矩的动态模型测量值,其中该模型的输入为静态模型式(6)中的扭矩Ts,输出为动态扭矩的测量值T(t),
T(t)=-a1T(t-1)-…-anT(t-n)
+b1Ts(t-1)+…+bmTs(t-m)。
(10)
2 分数阶PID控制器设计
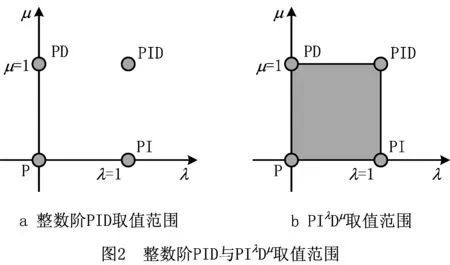
PIλDμ控制器[18]在整数阶PID控制器的基础上引入微分阶次μ和积分阶次λ两个可调参数,通过调节μ和λ的取值可以得到不同的控制(器)结构。如图2a所示,整数阶PID的微分阶次μ和积分阶次λ只能取0和1两个值,分别对应图中4个点,当μ=λ=0时为P(比例)控制;当μ=0,λ=1时为PI(比例—积分)控制;当μ=1,λ=0时为PD(比例—微分)控制;当μ=λ=1时为常规PID控制。图2b所示的阴影部分为PIλDμ控制器参数的微分和积分阶次的取值范围,因为λ和μ可以取任意值,其取值范围由整数阶PID控制器的“点”扩展为“面”,所以PIλDμ的控制形式更加灵活,可以获得更好的控制效果。
2.1 分数阶微积分及分数阶PID控制器原理
在分数阶微积分理论发展过程中,G-L (Grunwald-Letnicov)是分数阶微积分最广泛应用的定义之一[19],针对PIλDμ控制系统,G-L分数阶微积分定义[20]为
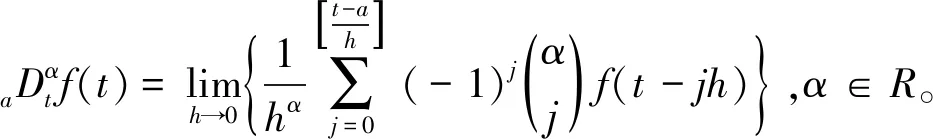
(11)


(12)
PIλDμ控制器的传递函数表达式为

(13)
式中:Kp,Ki,Kd分别为比例、积分和微分增益;λ,μ分别为积分阶次和微分阶次。
针对柔顺关节耦合器动态模型,PIλDμ控制器的单位反馈控制系统如图3所示,其中:Td(t)为系统输入,T(t)为系统输出,e(t)=Td(t)-T(t)为系统误差,I(t)为控制器输出。

2.2 基于理想Bode传递函数的PIλDμ控制器设计
基于理想Bode传递函数设计PIλDμ控制器的具体方法是:通过期望截止频率和相位裕量求出理想Bode传递函数,基于该开环传递函数和控制对象求出PIλDμ控制器。该方法设计的PIλDμ控制器对增益的变化具有很强的鲁棒性[21-22]。理想Bode传递函数为
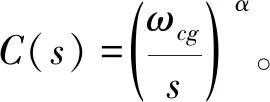
(14)
式中:ωcg为柔顺关节耦合器扭矩传递系统截止频率;α∈(1,2)。
基于理想Bode传递函数设计的PIλDμ使闭环系统对增益变化具有很强的鲁棒性,系统增益变化时将会使截止频率ωcg发生变化,但不会引起相位裕度φm=π-πα/2变化,这种对系统增益变化不敏感的特性正是柔顺关节耦合器扭矩传递控制系统所期望的。因此,基于理想Bode传递函数的这种特征设计PIλDμ控制器,可以使系统开环传递函数与理想Bode传递函数相同。闭环控制系统的性能指标ωcg和α之间的关系为:
σ%≈0.8(α-1)(α-0.75),1<α<2;
(15)
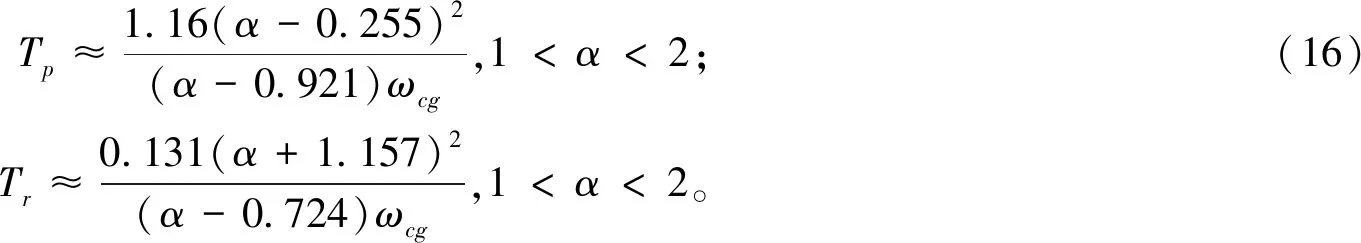
(17)
假设控制对象的传递函数为Cp(s),PIλDμ控制器的传递函数为Cc(s),理想Bode传递函数为C(s),

(18)
PIλDμ控制器的设计步骤如下:
(1)根据柔顺关节耦合器系统要求的频域截至频率ωcg和相位裕度φm计算理想Bode传递函数C(s)。
(2)根据上述闭环控制系统设计的时域指标计算ωcg和α。
(3)根据式(19)得出PIλDμ控制器的传递函数Cc(s)。
2.3 柔顺关节耦合器的扭矩控制策略仿真
利用理想Bode传递函数的频域设计方法可以分别得到PIλDμ和整数阶PID控制器的传递函数,PIλDμ控制器的传递函数为Cc(s) = 4.15+2.02/s1.13+35.13s0.81,整数阶PID控制器的传递函数为Cq(s) = 0.06+9.98/s+0.027s。在MATLAB/Simulink中建立两种控制器的闭环仿真系统,图4所示为柔顺关节耦合器扭矩控制系统的单位阶跃响应曲线,用于对比PIλDμ控制器和整数阶PID控制器的仿真效果。

从图4可以看出,无任何控制器作用的控制对象系统稳态周期较长,超调量较大,调节时间较长;而在PIλDμ和整数阶PID控制器作用下,系统的动态性能得到明显改善,超调量明显减小,上升时间和调节时间都明显减短,其中PIλDμ控制对系统阶跃响应的速度明显更快,调节时间更短,超调量近似为零。表2所示为系统单位阶跃响应的动态指标,同样可见PIλDμ控制器的超调量较小,响应较快,调节时间较短。
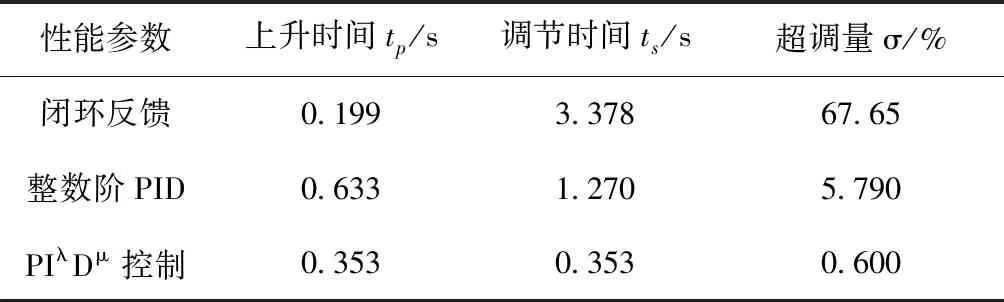
表2 单位阶跃响应
以一组单位正弦信号作为仿真系统的期望扭矩信号,图5所示为柔顺关节扭矩控制系统在PIλDμ控制器和整数阶PID控制器作用下对目标扭矩的跟踪控制效果。可以看出,PIλDμ控制器对期望扭矩的跟踪误差小于整数阶PID控制器,对目标扭矩表现出更好的跟踪控制效果。
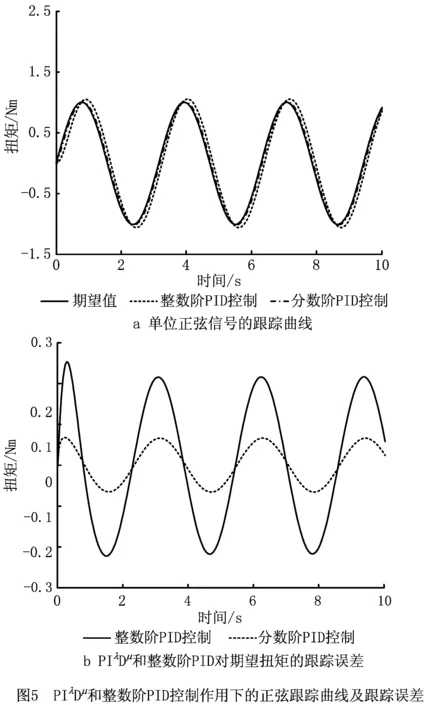
3 实验
为了验证PIλDμ算法的准确性,建立了柔顺关节耦合器实验平台,并基于LabVIEW图形化编程环境编写了PIλDμ和整数阶PID控制算法程序。实验平台和实验流程如图6所示,其基于NI PXI-1042Q机箱配置的多功能数据采集模块NI 6259和模拟输出模块NI 6704构成实验控制系统,可实现对系统数据采集、伺服电机转速控制以及程控直流电源的控制。伺服电机为柔顺关节耦合器系统提供动力,动态扭矩传感器输出扭矩信号,NI 6259采集模块将扭矩电压信号转化为扭矩数值,通过控制NI 6704输出模拟信号,使可程控直流电源为柔顺关节耦合器提供稳定、可调的直流电流,实验平台的主要产品如表3所示。

表3 柔顺关节耦合器产品型号
3.1 静态模型验证实验
根据磁流变液的Bingham-Plastic模型和Maxwell应力张量理论建立了柔顺关节耦合器扭矩传递的静态模型,根据MATLAB的System Identification Toolbox工具箱辨识得到相关设计参数。为了验证静态模型的正确性,实验以一组扭矩正弦信号作为柔顺关节耦合器系统的输入,图7所示为正弦电流作用下系统输出扭矩的测量值和估计值的变化曲线以及两者之间的误差曲线。
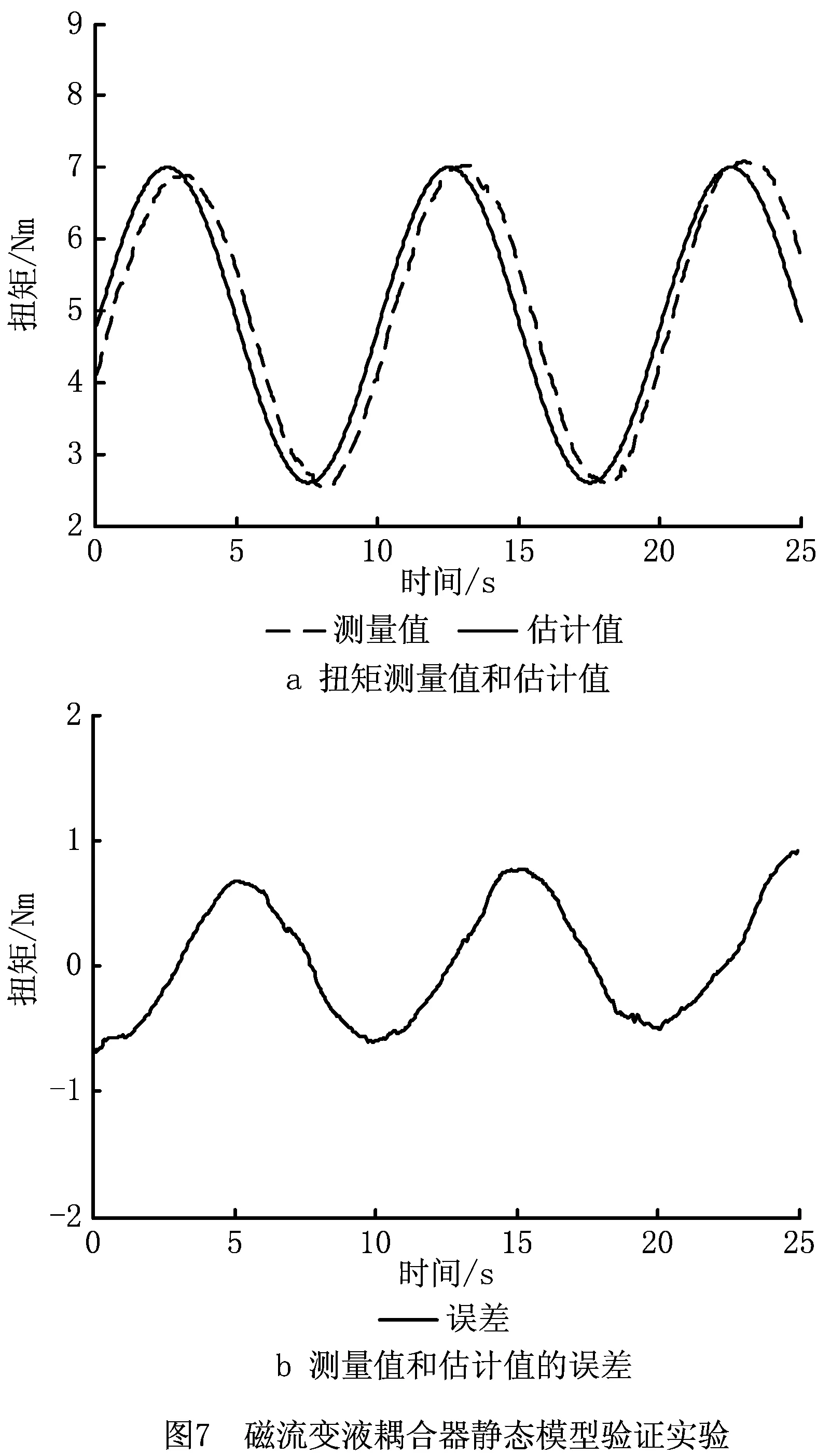
从图7 a可以看出,输出扭矩在某些时刻有一定波动,测量值和期望值也有一定相位延迟。估计值与测量值存在误差是由于:①在扭矩传动过程中,柔顺关节耦合器中的导磁材料存在磁滞;②安装过程中,柔顺关节耦合器在对中性上有一定误差;③可编程电源响应有一定延时,无法达到零延时响应;④建模过程中的忽略项引入了误差。
3.2 动态跟踪实验
为了进一步验证PIλDμ控制器在磁流变液柔顺关节耦合器扭矩控制过程中的优越性,分别以正弦波、三角波和方波信号作为期望输出扭矩,最大期望扭矩值均设为3 Nm。分别采用PIλDμ控制器和整数阶PID控制器对期望扭矩进行了跟踪控制,图8所示为3种波形的动态跟踪控制实验数据。
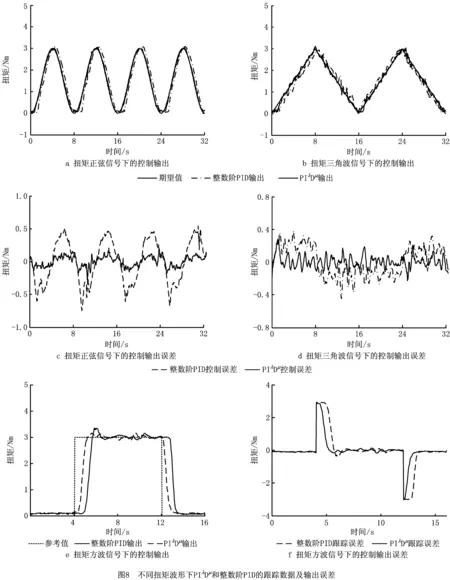
表4给出了不同控制器作用下的动态相应参数,对比发现在PIλDμ控制作用下,系统响应更快,超调量更小,达到稳态的时间更短。表5所示为PIλDμ和整数阶PID控制作用下的扭矩测量值与期望值之间的均方值误差和均方根误差,实验数据表明PIλDμ控制器对柔顺关节耦合器扭矩的控制具有更小的均方值误差和均方根误差,对期望扭矩的控制精度优于整数阶PID控制器。
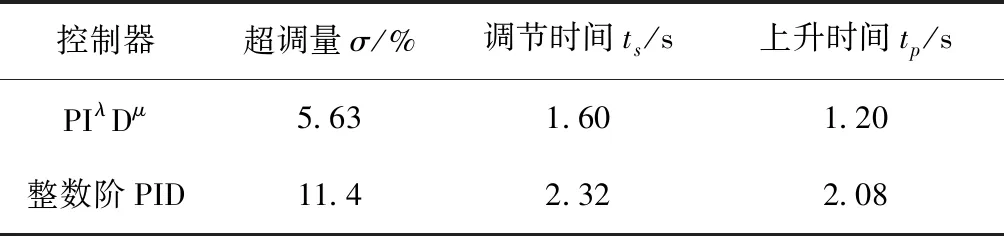
表4 柔顺关节耦合器阶跃响应

表5 整数阶PID与PIλDμ的均方值误差MSE和均方根误差RMSE
4 结束语
本文基于磁流变液多片式耦合传动装置设计了一种机器人柔顺关节,其中利用磁流变液的可控流变特性控制机器人柔顺关节的可变刚度,并结合Bingham-Plastic模型和Maxwell应力张量理论建立了柔顺关节耦合器的静态模型。基于自回归原理建立了柔顺关节耦合器的动态模型,并提出一种基于PIλDμ算法的动态扭矩控制方法,利用理想Bode传递函数的频域响应方法设计了PIλDμ控制器。采用MATLAB/Simulink对柔顺关节耦合器的动态扭矩控制系统进行了仿真,仿真结果表明PIλDμ控制算法对系统动态扭矩的控制比整数阶PID算法更优。最后搭建了柔顺关节耦合器动态扭矩控制实验系统,基于LabVIEW图形化语言分别开发了PIλDμ控制程序和整数阶PID控制程序,通过实验验证了PIλDμ控制算法的有效性和优越性。未来的研究将考虑将柔顺关节耦合器应用于下肢关节康复机器人,本文为今后集成应用磁流变液与传统康复机器人关节并实现关节的可变刚度控制提供了理论依据。

