基于物理的雾凇生长模拟算法

李 晔 ， 杨 猛 ， 上官大堰 ， 杨 刚

(1. 北京林业大学信息学院，北京 100083；2. 北京林业大学艺术设计学院，北京 100083)

雾凇是在低气温下，由空气中尚未凝华的水蒸气在树枝等物体上不断积累冻结粘连的结果。我国的一些地区由于其独特的气候特征以及地势地貌，每年都会形成雾凇这种独具风韵的景观，同时这些地区也是气象部门重点关注的对象，因为在特定情况下，长时间的雾凇天气会导致树木、高压线等被附着物积冰[1]，从而引发灾害事故，严重时可危害人民的生命财产安全。

自然界中的雾凇主要分软淞和硬淞2种。软凇结构松散，稍受振动就会脱落，密度小，形状类似于冰晶，是一种特殊的自然景观，如图1(a)和(b)所示；硬凇是空气中的雾滴随疾风移动，遇到物体迅速冻结粘连的结果，形成速度很快，结构紧凑、密度大、排列整齐，如图 1(c)和(d)所示。

图1 自然界中的软凇和硬凇图

雾凇的外观、外形极其不规则，没有均匀的表面且随着生长时间变化，最主要的是在周围环境发生变化时，其呈现的状态各异，具有极高的随机性。因而利用计算机图形学生成场景时，巨大的计算量往往会成为实时显示场景的瓶颈。

受WITTEN和SANPER[2]提出的扩散限制凝聚(diffusion limited aggregation，DLA)模拟金属粒子聚集方法启发，本文使用DLA的方式对软凇的形成形态进行模拟，并考虑了风力对于粒子凝聚产生的影响；同时在风环境中，通过对雾凇生长过程中的受力分析，使用分节计算生长终点的方式对硬凇的形态进行模拟。

本文提出了一种基于物理的雾凇生长动态模拟算法，通过引入覆冰模型、材料力学模型、风场、DLA方法，模拟风环境条件下的软凇和硬凇，特别是其生长方向和形态。

1 相关工作

1.1 冰凝结模拟

最早对晶体凝结过程进行模拟的方法是由KHARITONSKY和GONCZAROWSKI[3]提出的一种简单的冰柱形成方法，虽然模拟方式十分简便，计算速度也非常快，但并未达到真实的效果。

DLA是一种非常受欢迎的晶体生长方法，最初是文献[2]为了模拟金属颗粒的聚集而开发的，但该算法也被推广到许多其他自然现象的建模，包括雪花生长等[4-5]。张倩等[6]通过观察液体在固体冷表面上逐渐凝结生长的过程和特点，在原始分形理论的基础上，提出了双分支树状DLA模型，同时考虑冰晶表面在凝结过程中的散热量，模拟出了固体冷表面的霜晶凝结过程随时间变化的细节，并取得了极佳的效果。但是该方法并未考虑风条件对冰晶形态产生的影响，而是在相对理想的条件下对冰晶进行生长模拟。

除了DLA方法，相场方法也是一种常用的晶体生长的方法。KOBAYASHI[7]以文献[8]为基础对物理学中的凝结方向进行了研究，首次成功地将相场应用于雪花的生长过程的模拟中，并取得了十分真实的效果。除了相场方式之外，水平集方法在模拟晶状结构[9]方面也取得了成功，并且可实现更高的数值精度，但代价就是受限的计算速度。

文献[10]提出了一种基于物理的模拟冰晶凝结的新算法，结合 DLA、相场方法和稳定的流体解算器来控制冰的生长方向和形态，其得到的效果非常真实但是计算速度受到了一定的限制。随之又在前面工作之上，引入一个额外的自由度，即方向场，并由温度场和相场共同控制[11]，从而实现晶体模拟，利用高斯卷积加速计算，最后达到了十分真实的效果，但实现过程相对复杂。本文利用 DLA的方法模拟软凇形成，其类似于大气粒子凝结的现象，并考虑风力对雾凇形成造成的影响。

1.2 风场模拟

风在自然景物模拟中扮演着十分重要的角色，如风作用下树枝的摆动动画模拟、树叶飘落模拟、海面随风波动模拟等等，都需要对当前环境中的风进行模拟。目前已经提出很多关于风的模型，如空气动力学模型[12]、基于物理的风力模型[13]等。罗胜华[14]在空气动力学的基础之上，通过风速来计算作用在物体上的风力，并引入噪音技术体现风的动态效果，同时模拟风条件下树木的运动效果，但该方法对于具有非常复杂结构的树木模型时，计算速度是瓶颈。本文参考文献[15]的方法，利用柏林噪声函数来模拟风场，模拟速度很快，且能很好地体现自然界中风的随机性，但缺点是会产生连续时间段内风的变化非常剧烈或基本未变化的情况而导致结果出现不自然的现象。因此本研究在柏林噪声函数的基础之上增加了平滑函数，既能快速地模拟风场，又能在一定程度上减少出现剧烈变化或变化不明显的不自然现象。

2 本文算法

雾凇是气温低于-2℃时，雾中无数的雾滴逐渐凝结而成，而在风的影响下会产生软凇和硬凇2种不同的雾凇。软凇在风力较为平缓的情况下，薄雾中的小水滴粘附到物体的外表面时形成；硬凇是在风速较高的环境下，形成于树枝或其他固体的迎风面。

本文算法流程如图2所示。算法开始于对用户设定的当前模拟温度和风速的判定，若温度T大于等于T′ (实验中T′取-2℃)，则不满足生长雾凇的条件，系统提示用户是否重新输入温度；若温度小于T′，则满足雾凇生长的温度条件，根据温度、空气湿度、风速等条件计算雾凇的生长点D以及生长长度Lw。然后根据风速判断雾凇种类，若风速V小于等于V′ (V′=5.4 m/s)，则为软凇，可利用DLA方法模拟其形态；若风速V大于V′，则为硬凇，利用分节计算生长终点的方法模拟其形态，通过对每一节硬凇进行受力分析求出下一节硬凇。

图2 雾凇模拟算法流程图

计算机中数据的表述均是离散的，将树木模型上雾凇的生长离散化为在具有Mesh结构(点、线、面等)表示的树木几何面片上生长，假设某一个三角面片上有若干生长点，每个生长点上都对应着不同的雾凇长度、生长方向和雾凇形态。

如图3所示，ΔABC是导入树枝几何模型上的某一个三角面片，点D，Dn1，Dn2，Dn3，Dn4是当前三角面片上的生长点；向量e是生长点D上对应雾凇的生长方向；单枝长度为Lw；向量n是三角形面片ΔABC的法向；风向为向量Φ；风速为V。

图3 模型三角面片示意图

2.1 雾凇生长点

通过导入树木模型，本文在模型三角面片表面进行雾凇生长，并通过随机取点的方式得到雾凇的生长点。每个三角面片上生长点的个数由三角面片的法向与风向的夹角决定，夹角越接近于零，说明风向与三角面片近似垂直，则与雾滴发生碰撞凝结的可能性大，此时生长点数量多，反之生长点数量少。如图 3所示，计算每个三角面片上生长点数量，即

其中，n为三角面片的法向；Φ为风向；Nmax为三角面片最大生长点数，本文在软凇、硬凇模拟时Nmax分别取5和10。

2.2 雾凇生长长度

雾凇的生长长度与风速、冻结系数、被附着物的横截面积、生长时间等有关，因此本文引入覆冰模型来计算雾凇[16]的长度，即

其中，Lw为雾凇的长度；ρ为覆冰密度并可以由公式得到，T为温度。由于雾凇属于干增长的过程，因此冻结系数β取值为1.0；W为空气湿度，本文取值0.5；τ为雾凇的形成时间；V为风速；θ为雾凇生长方向与水平方向的夹角；捕获系数E为被附着物的横截面积与覆冰后的横截面积之比，反映了空气中雾滴的聚集效率。

2.3 风场模拟

自然界中的风可以由风速和风向2个量表示，且均具有不均匀性和随机性，而柏林噪声能够很好地模拟自然界中存在的一些随机性。本文中的风场在柏林噪声的基础上，增加了平滑函数使得模拟的结果更加自然，其采用的柏林噪声函数为

其中，p为振幅；α为频率；N为倍频；x，y，z分别为计算柏林噪声点的坐标；sin(ωt+)β为平滑函数；t为生成时间；Noise函数可平滑、插值随机数生成器生成的随机数。本研究选择相对变化不剧烈的风，因此采用大幅度低倍频，p取2，α取0.5，N取 4。Noise函数是创建的随机数生成器，其在(-0.5，0.5)之间生成随机数，根据输入的参数，可输出基于当前参数的随机数，如果再次输入的参数与之前的某一个参数相同，那么其输出的结果也是一样的。

平滑前、后的柏林噪声函数曲线如图4所示。

计算同一时刻生长点D的风速，即

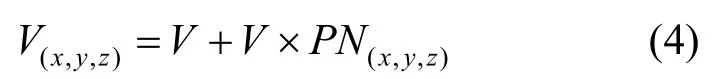
其中，V(x,y,z)为生长点D处的风速；V为用户输入的风速；PN(x,y,z)为柏林噪声；参数x,y,z为生长点D对应的坐标。

自然界中风的方向具有很大的随机性，主要是因为风可分为大风和微风。大风特点是风速大，同一高度平面内的风向大致相同且与地面平行，如图5(a)所示，其生成的是硬凇；微风的特点是风速小，风向不定，同一时刻、同一高度平面内各方向的风都存在且与地面平行，如图5(b)所示，在微风环境下生成的是软凇。

图4 平滑前、后的柏林噪声函数示意图

图5 同一高度平面内不同风型的风向示意图

因此将空间中任意一点的大风风向表示为Φ=(sint, 0 ,cost)，其中t为[0,2π]之间的随机数。微 风 表 示 为Φ=(-cost1, 0,sint2)， 其 中t1,t2∈ [ 0,2π]，t2=trand× ( 1 +Nrand)，trand为[0,2π]之间的随机数，Nrand为通过柏林噪声计算得到的(0，0.5)之间的随机数。

2.4 软凇模拟

2.4.1 软凇生长方向

软凇生长在风速较小的环境中，因此其最终的生长方向由自身的生长方向与风向共同决定。生长方向是在生长点所在三角面片的法向n添加一个随机扰动向量得到。如图 3所示，向量n和点D分别为三角面片法向和雾凇生长点，点E为三角面片上点D附近的一点，向量DE作为扰动向量，与风向Φ、法向n之和得到软凇最终的生长方向e。

2.4.2 软凇形态

软凇的形态类似于片状晶体，本文利用 DLA的方法生成片状晶体的形态。为保证最终形态的片状结构，首先将生长点映射到XOY平面，而后以XOY平面上的生长点为凝聚核，雾凇长度为逃逸半径，各个粒子进行凝聚生长，凝聚过程如图6所示。

图6 凝聚模型示意图

D′为图3中生长点D映射到XOY平面后的凝聚核，P1，P2分别为第1次和第2次产生的粒子，l1，l2是其运动轨迹。通过在半径为Lw的逃逸圆周内的行走，P1与凝聚体发生凝聚，P2则脱离了圆周，未与凝聚体发生凝聚。软凇形态模拟算法如下：

(1) 将XOY平面上映射的生长点作为凝聚核D′，并设置凝聚体最大的粒子数n_max为20。

(2) 以雾凇长度Lw作为逃逸半径画圆，圆内为有效区域。

(3) 在有效区域内随机产生 1个粒子，坐标Pi(Xi,Yi)为

其中，Rrand为(0,Lw)之间的数，保证产生的粒子在有效区域内；αrand为[0,1]之间的数；D′x和D′y分别为凝聚核的x,y坐标。

(4) 该粒子按照一定的规律进行游走，若运动到凝聚核附近，则与凝聚核发生凝结，回到步骤(3)产生第2个随机粒子；若运动到逃逸半径之外，则直接回到步骤(3)产生第2个随机粒子。

(5) 粒子每运动一次都需判断是否到达了凝结核和已凝结的粒子附近，当凝聚体的粒子数到达n_max后，停止产生新粒子，得到软凇形态的片状结构。

(6) 在XOY面形成的软凇片状结构旋转到生长点所在三角面片的法向与生长方向组成的平面，得到最终的软凇形态。

模拟过程中最重要的是粒子的行走规律。根据对流扩散方程，粒子浓度与风速之间的关系满足式(5)[17]，即

其中，C为粒子浓度；X，Y分别为粒子二维空间中坐标的x，y分量；Vx为风速x方向的分量；Vy为风速y方向的分量；设∂X=Δx；∂Y=Δy。则粒子浓度与粒子坐标之间的离散表示形式为

本文设粒子在行走的过程中，只会从当前位置选择一个四邻域位置进行移动。在没有任何外力场影响的纯扩散条件下，从当前位置移动到4个位置的概率是相等的，加入风场因素之后，粒子浓度与粒子运动的概率关系[17]满足式(11)，即

其中，PX+1,Y，PX-1,Y，PX,Y+1，PX,Y-1分别为粒子从点(X+ 1 ,Y)，(X- 1 ,Y)，(X,Y+ 1 )，(X,Y- 1 )运动到点(X,Y)的概率。由式(10)和式(11)得到粒子运动概率方程为

本文中 Δx, Δy的取值范围为根据上述运动概率方程，粒子从当前位置移动到下一位置，移动距离为 Δx, Δy，同时判断其八邻域内是否存在粒子，若存在，则进行凝聚，并产生下一个粒子，直到凝聚体的粒子数到达n_max。

图 7为雾滴粒子在不同风力作用下的凝结效果示意图，其中空心圆表示凝聚核，实心圆表示凝结体。图7(a)是在无风力作用的理想状态下，使用传统的扩散凝聚方法，呈现出类对称性生长的凝聚体形态。图7(b)和(c)分别是在不同风速条件下的凝聚体形态，可以看出随着风速的增加，对凝聚体的形态有着非常明显的影响作用，雾滴粒子主要在迎风侧发生凝聚，背风侧凝聚的粒子相对较少。

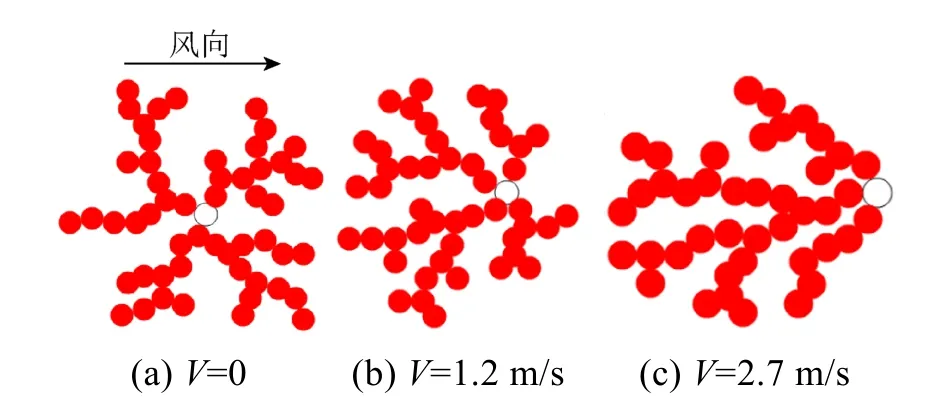
图7 不同风速下凝聚体结构形态

2.5 硬凇模拟

硬凇的生长在风速较大的环境中，风对其生长方向的影响远远大于其自身的生长方向。因此本文直接将风的方向作为硬凇的生长方向，并利用分节的方法模拟其形态，根据每一节雾凇的生长点和长度，对其受力分析，计算出下一节的生长点。

2.5.1 硬凇每节长度

硬凇每一节的长度Lwi计算公式为

其中，Lw为雾凇总长度；r为生长节数；γwi为随机系数；i=1,2,3,···,r；γw1+γw2+γw3+···+γwi=1。

2.5.2 硬凇形态

图8为硬凇的形态示意图。

图8 硬凇的模拟形态示意图

图 8中点D是树模型三角面片上硬凇的一个生长点，点D1，D2，D3分别为第1节、第2节、第3节的生长终点，其之间的关系为

其中，r=1,2,3,···,Dr为当前节的生长终点；Dr-1为当前节的生长点，也是前一节的生长终点；Δd为风力作用下，生长点相对于生长终点的偏移量。根据胡克定律，雾凇所受的弹力Fi满足

其中，μ为冰晶的刚度系数；Δd为在力的作用下的形变量，即风力作用下雾凇生长终点相对于生长点的偏移量；Si为雾凇的面积；Ei为冰晶的弹性模量，气温在[-19.0，-1.0]摄氏度之间时，冰晶的弹性模量为[5.0，6.0][18]，因此Ei取[5.0，6.0]之间的随机数；Δl为弹力作用下雾凇的形变量；Lw为雾凇的长度。化简得到雾凇刚度系数与杨氏模量之间的关系为：μ=Ei×Wi，其中Wi为雾凇的宽度。

将式(18)带入式(19)，得到雾凇所受弹力与偏移量的关系式为

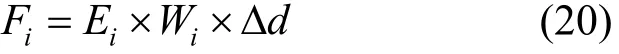
由动量定律，可得其中，mg为风的质量，满足mg=ρSg Vwt，ρ为空气密度，取标准状态下空气密度值为1.29，Sg为迎风面积，Vw为风速。雾凇满足受力平衡，有Fi=Fg，最终求得风力作用下雾凇生长终点相对于生长点的偏移量Δd的横向偏移量Δdx和纵向偏移量Δdy分别为

其中，对于软凇，Δαi-g为雾凇生长方向与风向的夹角；对于硬凇，Δαi-g为风向。最终将每一节进行连接，得到硬凇的形态。

2.6 穿刺处理

在雾凇生长模拟的过程中，存在 2种穿刺现象：①生长出的雾凇与树干之间的穿刺现象；②生长出的雾凇与雾凇之间的穿刺。如图9所示，ΔABC是模型中一个三角面片，法向为n，生长点D1，D2，D3分别对应3个雾凇的生长点，且生长点D3对应雾凇发生第1种穿刺现象，生长点D1，D2对应雾凇在虚线圈部位发生第2种穿刺现象。

对于第1种穿刺现象，若雾凇的生长方向e与生长点所在三角面片的法向n之间满足：e·n≤0，则说明雾凇与树干之间发生了穿刺现象，则该生长点不生长雾凇。对于第2种穿刺现象，设当前雾凇的生长方向为ecurr，生长长度为lcurr，则距离当前生长点为lcurr的所有生长点的生长方向enext分别进行相交判断，若发生了相交，则为enext添加一个扰动使其偏离原来的生长方向。

图9 穿刺现象示意图

3 实验结果

系统运行在配置条件为 Intel®CoreTM i5-3230M CPU 2.60 GHz，4 GB内存的PC机上，通过OpenGL导入。OBJ格式的树模型，用povray进行渲染。图10为软凇和硬凇在不同环境下、同一树枝上的模拟示意图，生长时间分别为5 h和10 h。图11为软凇和硬凇结构细节图，图12为渲染结果图；图13为软凇在树叶模型上的生长结果，可以看出本文算法适用于具有边缘结构的模型；图14为硬凇在折断树枝上的生长结果示意图，其引用了文献[19]模型；图15(a)为软凇在松树树枝模型上的模拟结果，图 15(b)为软凇在松树树枝上生长的真实图片；图 16为文献[6]利用 DLA的方法模拟出的冷表面霜晶的生长结果；图17为雾凇细节模拟结果与现实的对比。表1为该树枝上雾凇生长处理的点、面数量以及绘制时间等数据统计表。

图10 不同参数控制下软凇和硬凇模拟效果图

图11 软凇、硬凇局部细节结构模拟效果图

图 12 软凇(图(a)～(c))和硬凇(图(d)～(f))的渲染效果图

图13 更多边缘结构生长渲染效果图

图14 雾凇作用下树枝断裂效果图

图15 软凇在松树上的模拟结果图和真实图

图16 本文方法与文献[6]方法生成的凝聚体

图17 雾凇模拟图与真实图对比

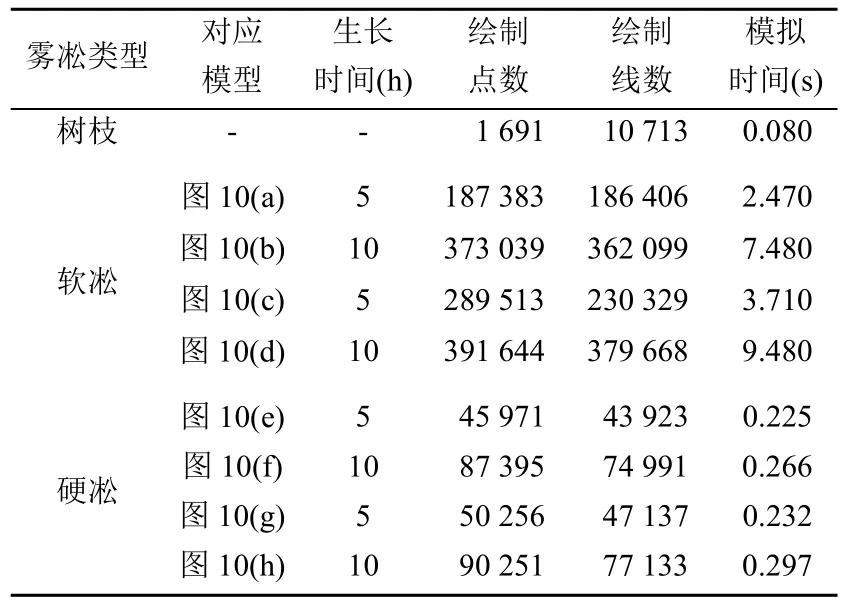
表1 树枝模型处理参数

由表1可以看出，随着生长时间的延长，模拟结果需要绘制的点、线数据有着明显的增加，特别是软凇，因软凇的形态相对复杂需要更复杂的点、线结构来表现其多样的形态，其代价就是模拟速度明显减慢。

图10通过横向2张图片进行对比可以看出：在温度、风速均相同的条件下，随着生长时间的增加，软凇和硬凇的生长长度和密度均有明显地增加，特别是硬凇的长度和密度，排列相对整齐，且集中在同一侧，这也是对树干、电线等被附着物产生巨大破坏力的原因。通过纵向5张图片进行对比可以看出：在温度、生长时间相同的条件下，风速对于雾凇的形态有很大的影响作用，风速越大，不仅会让雾凇的形态发生明显的变化，而且生长长度也有着非常明显的增加。

图16中文献[6]方法生成的凝聚体形态更加分散且随机性极高，更适用于理想状态下的冰晶生长。本文方法考虑了风对于冰晶形成过程中产生的影响，得到的凝聚体结构更加紧密，且受风向的影响较明显，更适用于雾凇这类受周围环境影响明显的凝聚现象。但在最后的渲染结果中，文献[6]方法增加了冰晶表面的细节，使得最后的结果更加真实自然，而本文在最后渲染中未进行雾凇表面细节的体现，这也是本文接下来的重点工作之一。

4 结 束 语

通过观察、分析自然界中软凇和硬凇的生长环境、生长形态，提出了基于物理的雾凇生长算法，主要对雾凇在环境影响下的生长形态、生长方向进行了研究。算法采用DLA的方法，考虑雾滴粒子在风场作用下在凝聚核周围的运动，最终形成软凇的形态，然后对雾凇在风力作用下进行受力分析，采用分节计算生长终点的方式模拟硬凇的形态。

本文算法对于近距离观察软凇和硬凇绘制效果最佳，能够很好地展示2种雾凇的结构、形态，对于具有一定边缘性结构的部位也有一定的适用性。但是对于雾凇的粗细、表面颗粒感等细节没有进行进一步的处理，因此接下来的重点工作之一就是增加雾凇的表面细节。

对于算法的计算效率，本文提出的 算法在模拟的过程中需要处理的点线面数据量较大，导致雾凇生成的速度较慢，因此未来需要进一步考虑利用GPU进行加速绘制。