对称区域边界处理方法及基于表面粒子提取的表面张力计算

朱晓临， 张义群， 郭清伟

(合肥工业大学数学学院，安徽 合肥 230009)

基于物理的流体模拟方法已广泛应用于影视特效、生物医疗、灾难预防与营救等领域，而边界处理及液体表面张力的计算一直是流体模拟研究的重要课题。

在光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法中，传统的流固边界处理方法有3种：密度正则化法、边界力法和虚粒子法。处理表面张力的方法为 2种：IIF方法(inter-particle interaction force)和CSF方法(continuum surface force)。

本文针对传统的边界力法和虚粒子法计算量大、对复杂边界处理难以达到实时性的问题，提出改进。

1997年，MORRIS等[1]提出了一种动态生成镜像虚粒子的方法，该方法对于直边界(边界为平面)效果很好，但对于复杂边界效果不佳；2002年，LIU等[2]将虚粒子法与边界力法相结合，提高了SPH近似在边界的精度，但需实时生成虚粒子，过程较为复杂；2006年，HU和ADAMS[3]将虚粒子看作另一种相，虚粒子关于边界对称铺设插值点，其只对直边界效果较好；2011年，MARRONE等[4]提出了一种只需在初始时刻生成虚粒子的方法，但其对复杂几何形状的场景，内部插值点构造复杂；2012年，SCHECHTER和 BRIDSON[5]提出 Ghost方法，用于流体自由表面和边界条件的处理，虚粒子具有较稳定的状态分布，但需要更多的预处理和计算量；2012年，ADAMI等[6]将流体粒子的压强赋值给虚粒子，利用状态方程反推出虚粒子密度。该方法适用于具有复杂边界的场景，但虚粒子的压强可能为负值，导致流体穿透边界；2015年，刘虎等[7]指出，该方法利用压强反推密度是多余的。文献[7]还将虚粒子看作流体粒子的扩展，虚粒子有条件地参与控制方程的计算，对流体粒子的压力、速度方向产生影响，但此方法对于复杂边界效果不佳；2017年，ESLAMIAN和KHAYAT[8]用靠近边界的2层粒子作为内衬层代替虚粒子，避免了边界力法施加人工力导致的动量不守恒问题和虚粒子法造成的不满足连续性方程的问题，但该方法必须耦合其他压力处理方法，否则会产生明显的视觉压缩，增加计算量。

针对上述方法计算量大、对于复杂边界处理效果不佳的问题，本文提出了对称区域边界处理方法。对于靠近边界的流体粒子，首先找到被边界截断的流体粒子的支持域，然后通过中心对称，在流体粒子支持域中找到关于被截断区域对称的区域，在计算流体粒子密度时，增大该对称区域内的粒子权重，避免了边界对粒子支持域截断带来的密度、压力计算错误等问题。与传统的边界力法和虚粒子法相比，本文方法无需生成虚粒子，在保证逼真度的前提下满足实时性要求，且随着粒子数的增加，耗时增长也明显比其他传统方法慢，计算效率高的优势更明显，更适合对复杂场景的模拟，同时避免了边界处流体与边界分离的现象。

本文的另一项工作是对传统的 CSF方法进行改进。

1992年，BRACKBILL等[9]提出 CSF方法，通过将流体表面描述为一个具有有限厚度的过渡带，并将表面张力转化为体积力进行计算，适用于任何形状的表面，但其用一个光滑的色函数区分2种流体是没必要的；2000年，MORRIS[10]将 CSF方法引入 SPH方法中计算表面张力，并采用光滑的色函数，但采用 SPH计算表面曲率时，散度的计算需要核函数的充分支持，而核函数在过渡带内是无法满足的；2005年，TARTAKOVSKY和MEAKIN[11]针对CSF无法满足表面张力的切向特性，提出了计算表面张力的公式，通过余弦函数定义吸引、排斥力来重现表面张力的影响。粒子运动具有较好的一致性，但计算得到的表面张力需要校准，且在液滴的模拟过程中会出现收缩、膨胀交替的过程，不符合表面张力作用的实际情形。文献[3]使用不连续的色函数解决了文献[10]的曲率计算问题，修正了表面张力计算公式，避免了表面张力方向错误的问题，但计算量相对较大。2007年，HU和ADAMS[12]将CSF方法应用于多相流的模拟；2010年，ADAMI等[13]提出一种新的散度近似方案，无须完整的核函数支持域，得到了精度较高的曲率，但其不完全遵守动量守恒；2017年，YANG等[14]将原始网格的每个顶点的表面张力强度转移到其相邻的粒子上，得到了较好的结果，但需多次迭代计算；2018年，KRIMI等[15]对文献[13]提出的表面张力计算方法进行改进，提高了流体表面附近的稳定性，考虑了表面张力的切向特性，并且可以应用于两相以上的流体模拟，但该方法依旧无法保证动量守恒。

针对 CSF方法将表面张力看作体积力进行计算导致的曲率计算脱离表面形状控制这一问题，本文对 CSF方法进行了改进，提出了基于表面粒子提取的表面张力计算方法：首先精确提取表面粒子，并通过表面粒子计算曲率，不但减小了传统CSF方法计算曲率的误差，而且减少了计算量，提高了计算速度。通过方形液滴实验，验证了该方法的有效性。

1 SPH方法

SPH方法是一种无网格插值法，通过核函数近似计算粒子的物理属性；描述流体运动规律的N-S

方程[16]为

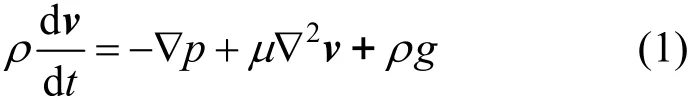
其中，ρ为密度；v为速度；t为时间；p为压强；μ为粘性系数；g为重力加速度。式(1)等号右侧依次为压力项、粘性力项、外力项。粒子属性通过离散求和公式[16]计算如下

其中，A(r)为位置r的目标粒子的属性值；N为目标粒子邻域内粒子总数；mj，ρj，Aj，rj分别为目标粒子邻域内粒子的质量、密度、物理属性值和位置；W(r-rj,h)为光滑核函数；h为光滑核半径。

A(r)的梯度和拉普拉斯算子通过离散求和式[16]分别计算如下

其中，∇为梯度算子；2∇为拉普拉斯算子。

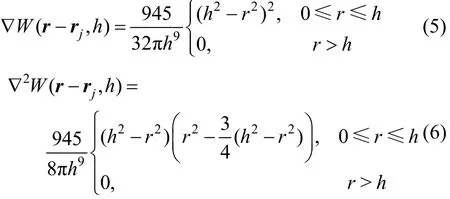
其中，r为目标粒子与支持域内粒子j的间距。

由式(2)得到流体粒子的密度公式[16]，即

对于弱可压缩流体，采用泰特方程[17]计算压强

其中，k为气体常数；ρ0为流体静止密度。

压力和粘性力计算[16]如下

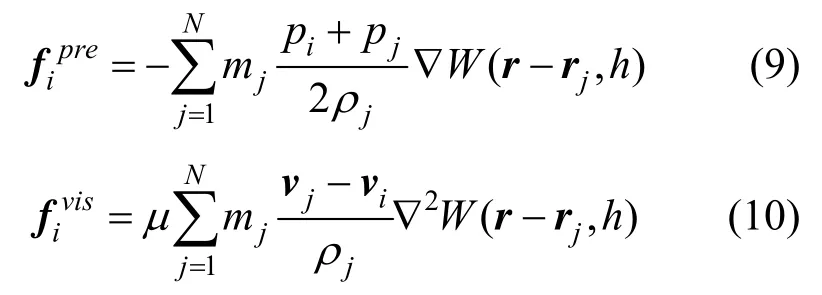
针对不同的物理量，采用 Muller的核函数，计算以下核函数：

(1) 密度核函数[16]

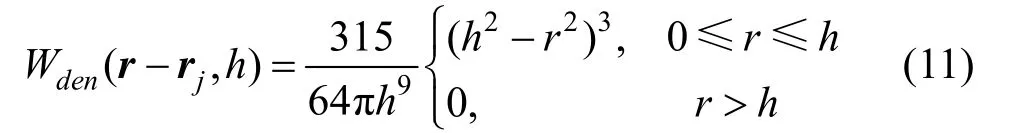
(2) 压力核函数[16]

(3) 粘性力核函数[16]

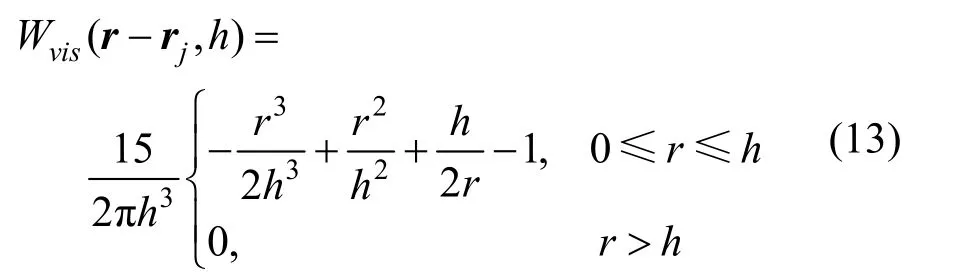
其中，r为目标粒子与支持域内粒子j的间距。

2 对称区域边界处理方法

边界力法是在边界铺设一层粒子并对流体粒子施加作用力，防止粒子穿透，该方法需要求解边界力，足够小的时间步长才能保证模拟的稳定性。虚粒子法通过在边界另一侧镜像生成流体粒子，并给其粒子赋密度和压强来降低截断误差，该方法需要铺设虚粒子，随着粒子数的增加计算量增大；对于复杂边界，难以确定虚粒子的位置，使得算法复杂度提高，因此传统的边界力法和虚粒子法难以满足实时性要求。为此，本文提出一种对称区域边界处理方法。以下分直边界、圆边界、锯齿边界3种情形进行讨论。

(1) 直边界。对靠近边界的粒子i的支持域，首先找到被边界截断的区域2；再确定支持域中与区域2对称的区域1；然后计算粒子的密度：计算区域3内的粒子的密度时，按正常权重计算；计算区域1时，将其权重增大到原权重的2倍，如图1所示。

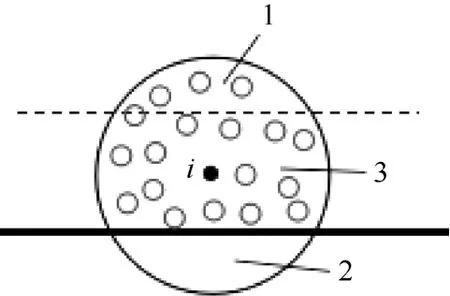
图1 直边界的情形

图1中，粗直线表示固壁边界，虚线与粗线关于粒子i对称，大圆表示粒子i的支持域，小圆圈表示支持域内的其他流体粒子，区域 2表示支持域被边界截断的部分，区域1与区域2关于粒子i对称。

对于直边界，当粒子碰到边界时，若粒子速度为v，将v在边界方向和与之垂直的方向进行分解，于是反弹后的速度为

(2) 圆边界。设圆形边界所在的圆为以点O为圆心，R为半径的圆O；对靠近边界的粒子i，圆O关于i对称的圆为圆O′。对粒子i的支持域，首先找到被边界截断的区域5；再确定支持域中与区域5对称的区域4；然后计算粒子的密度：计算区域6内的粒子的密度时，按正常权重计算；计算区域4内的粒子的密度时，将其权重增大到原权重的2倍。如图2所示。

图2中，粗线圆为固壁边界所在的圆，虚线圆与粗线圆关于粒子i对称，中间的圆为粒子i的支持域，小圆圈表示支持域内的其他流体粒子，区域5表示支持域内被边界截断的部分，区域4与区域5关于粒子i对称。

图2 圆形边界的情形

当粒子到达边界时会发生反弹，直边界反弹处理比较简单。对于圆形边界，v在切线和垂直切线的方向进行分解，得到切向和法向速度，即

其中，α为速度与法向的夹角；vt为切向速度；vn为法向速度，如图3所示。

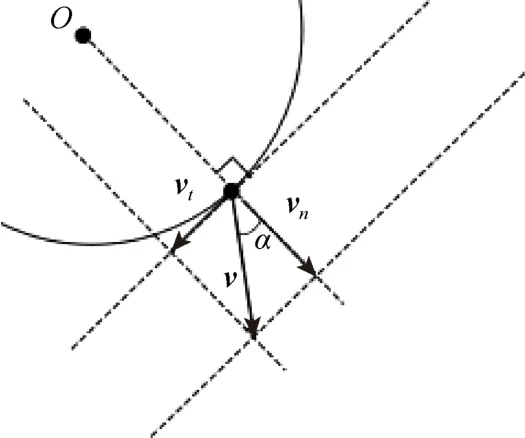
图3 圆形边界速度处理

转换到直角坐标系后，反弹后的粒子速度为

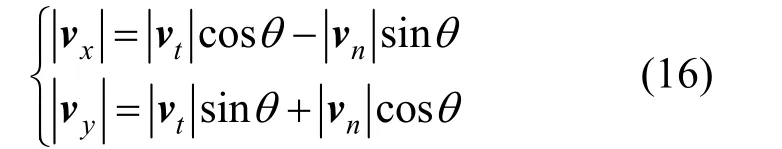
其中，θ为切线方向与水平方向的夹角。

(3) 锯齿边界。对靠近边界的粒子i的支持域，首先找到被边界截断的区域8；再确定支持域中与区域8对称的区域7；然后计算粒子的密度：计算区域9内的粒子的密度时，按正常权重计算；计算区域7内的粒子的密度时，将其权重增大到原权重的2倍，如图4所示。

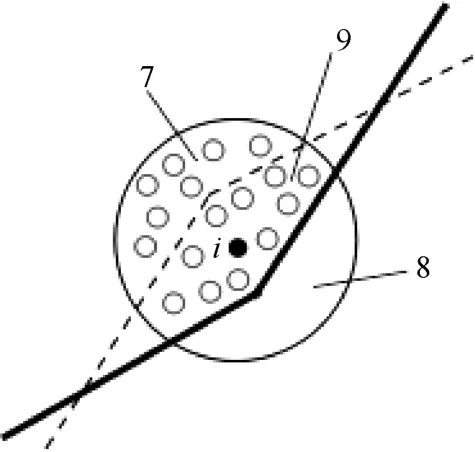
图4 锯齿边界的情形

图4中，粗直线表示固壁边界，虚线与粗线关于粒子i对称，大圆表示粒子i的支持域，小圆圈表示支持域内的其他流体粒子，区域 8表示支持域被边界截断的部分，区域7与区域8关于粒子i对称。

对于锯齿边界，其速度反弹的处理方法与圆形边界速度反弹处理方法相同。模拟仿真效果见4.1节。

3 基于表面粒子提取的表面张力计算

CSF方法通过将流体表面描述为一个具有有限厚度的过渡带，将表面张力转化为体积力进行计算。2种流体分别被赋予了不同的颜色值，如研究液滴的表面张力时，将液体粒子的色值设为1，将空气粒子的色值设为0，根据SPH思想得到一个色函数，通过计算得到每个粒子相应的色函数值，当其大于阈值时计算表面张力。

在运用 CSF的过程中，虽然流体粒子整体分布是均匀的，但就局部而言，流体粒子分布并不均匀，致使表面曲率计算错误，从而导致表面张力的计算错误。

因为表面张力是一种表面力，曲率的计算只与表面的形状有关。为此，本文对 CSF方法进行了改进，提出了一种基于表面粒子提取的表面张力计算方法。

提取表面粒子，首先要确定该粒子是表面粒子，下面给出判断表面粒子的方法。以粒子i为向量起点做2个相互垂直的向量a和b，将粒子i的支持域内的粒子j以粒子i为起点做向量xij，并与向量a和b的数量积的正负来判断粒子i是否为表面粒子。若粒子i支持域内所有粒子j满足a·xij＜0或b·xij＜0，则说明从向量a到向量b的圆心角为90°的扇形区域内没有粒子，粒子i为表面粒子；否则，将向量a和b同时旋转，当旋转到某个角度(设这个角度为α(0＜α＜2π))，粒子i支持域内所有粒子j都满足a·xij＜0 或b·xij＜0，则停止旋转，此时粒子i为表面粒子；若向量a和b同时旋转，直到转回初始位置，粒子i支持域内所有粒子j均不满足a·xij＜0 且b·xij＜0，则粒子i不是表面粒子。如图5所示。

图5中，黑色实心小圆分别为粒子i的2种情况，虚线圆为粒子i的支持域。①粒子i位于图中上方，此时i的支持域中从向量a到向量b的扇形区域内无其他流体粒子，此时i为表面粒子；②粒子i位于图中下方，此时i的支持域中，无论向量a和b如何旋转，向量a与向量b之间的扇形区域内均有其他流体粒子，此时i不是表面粒子。

图5 表面粒子提取

下一步根据提取出的表面粒子计算曲率。将2种流体粒子的色值分别设置为1和0，其色函数[16]为

在CSF模型中，表面张力计算模型[16]为

其中，σ为表面张力系数；单位法向n= ∇cs；曲率κ=-(∇ ·n) = -∇2c。具体计算如式(3)～(6)。

计算曲率时，目标粒子i邻域内的粒子是通过上一步表面提取得到的边界粒子。模拟仿真效果见4.2节。

4 仿真实验与分析

实验在 Windows 7平台上进行，开发环境为visual studio 2013，实验配置为Intel(R) Core(TM)i5-2400，3.10 GHz CPU，4 G 内存，NVIDIA Geforce GT 620 显卡。

4.1 二维溃坝流固边界处理仿真实验

为了验证本文提出的对称区域边界处理方法的有效性，将边界力法、动态虚粒子法、静态虚粒子法及本文方法分别应用于二维溃坝场景的直边界处理(图 6～8，表 1)，比较模拟效果，粒子数分别为1 156，2 809，5 329。再将上述3中传统方法及本文方法分别应用于二维溃坝场景的圆边界处理(图 9～11，表 2)及锯齿边界处理(图 12～14，表 3)，比较模拟效果，粒子数分别为1 550，3 010，5 712。实验时间步长取0.005 s，初始密度取1 000 kg/m3，粒子支持域半径取0.04 m。

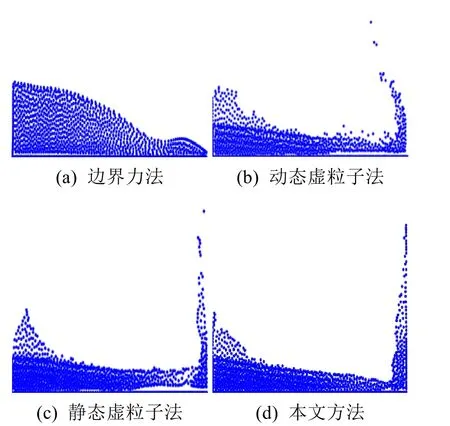
图6 直边界情形下，4种方法在第230帧时的模拟效果(粒子数为1 156)

图7 直边界情形下，4种方法在第230帧时的模拟效果(粒子数为2 809)

图8 直边界情形下，4种方法在第240帧时的模拟效果(粒子数为5 329)

表1 直边界情形下，4种方法在不同粒子数及帧数时运行耗时表(s)

图9 圆边界情形下，4种方法在第170帧时的模拟效果(粒子数为1 550)

图10 圆边界情形下，4种方法在第160帧时的模拟效果(粒子数为3 010)

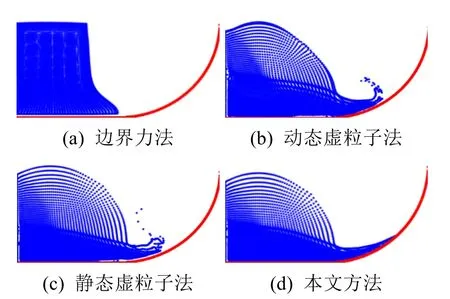
图11 圆边界情形下，4种方法在第120帧时的模拟效果(粒子数为5 712)

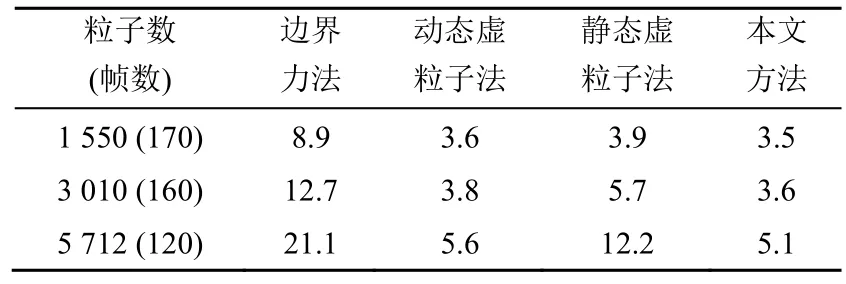
表2 圆边界情形下，4种方法在不同粒子数及帧数时运行耗时表(s)

图12 锯齿边界情形下，4种方法在第210帧时的模拟效果(粒子数为1 550)

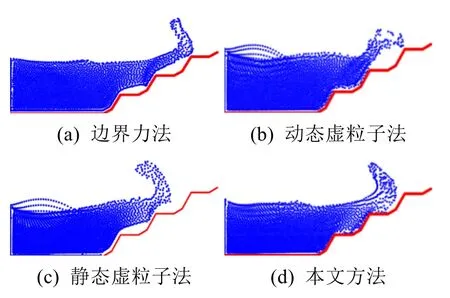
图13 锯齿边界情形下，4种方法在第196帧时的模拟效果(粒子数为3 010)

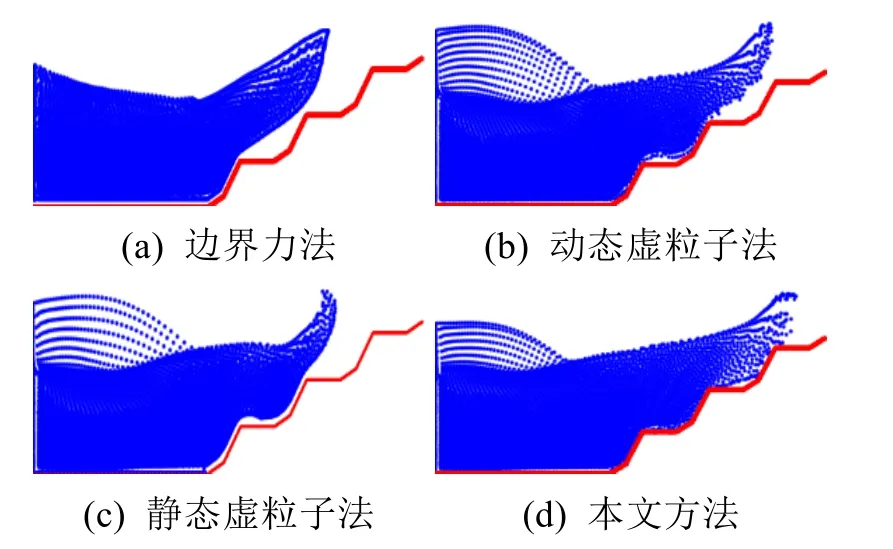
图14 锯齿边界情形下，4种方法在第196帧时的模拟效果(粒子数为5 712)

表3 锯齿边界情形下，4种方法在不同粒子数及帧数运行耗时表(s)

由图6～14可以看出，静态和动态虚粒子法会出现由于虚粒子产生的压强过大导致的流体与边界分离等不稳定现象；边界力法由于时间步长的限制导致模拟速度缓慢；本文方法不仅不会出现上述问题，而且模拟效果稳定、符合实际。由表1～3可以看出，本文方法在很大程度上减小了计算量，且随着粒子数的增加，本文方法实时性的优势更加明显，这为复杂边界的处理提供了基础。

4.2 形成圆形液滴的仿真实验

在处理表面张力时，本文可精确提取表面粒子，通过表面粒子计算曲率，减小了传统 CSF方法计算曲率的误差，提高了模拟效率。

在进行圆形液滴形成的模拟实验中，实验粒子数为1 024，粒子支持域半径为0.04 m，时间步长为0.02 s。图15为表面粒子提取效果，其中红色粒子为内部粒子，蓝色粒子为表面粒子。图16为文献[11](利用余弦函数计算表面张力)、传统CSF方法及本文方法模拟圆形液滴形成过程的效果对比。

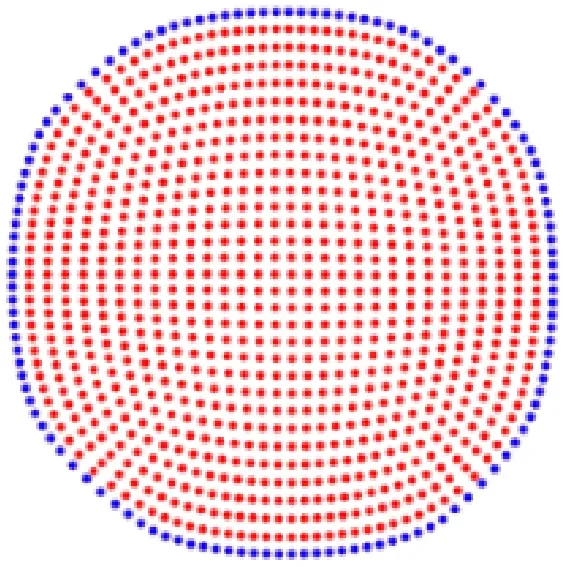
图15 表面提取效果(蓝色粒子为表面粒子，红色粒子为内部粒子)

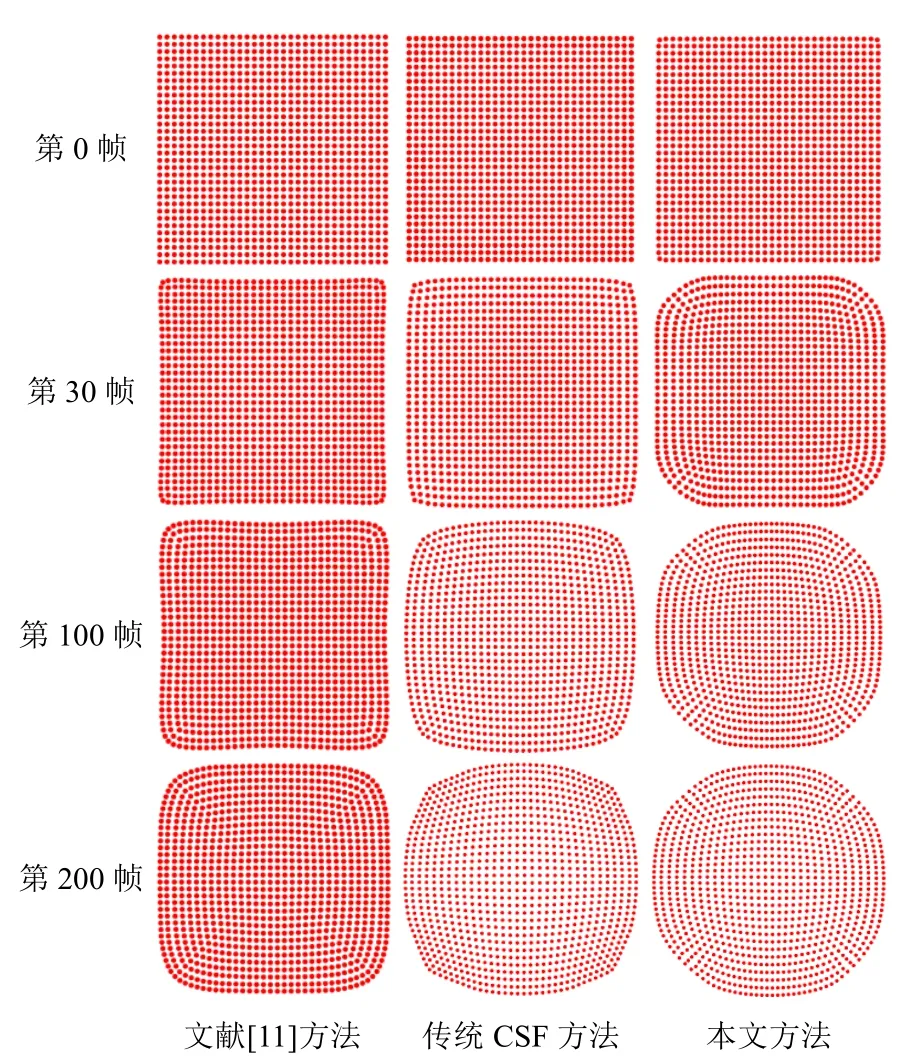
图16 3种方法模拟液滴形成不同时刻的模拟效果

图16中3种方法运行到200帧时，耗时分别为4.5 s，4.2 s，3.5 s，可以看出，与文献[11]的方法相比，本文方法在帧数为200时已经得到了很好的效果，而文献[11]方法的液滴还处于变化状态。此外，本文方法的液滴在整个变化过程中一直处于扩张状态，而文献[11]方法会出现收缩、膨胀交替的过程，不符合表面张力作用的实际情形；与传统CSF方法相比，本文方法形成的圆形液滴更光滑。总之，本文方法模拟圆形液滴形成时，不但效果好，而且耗时短。

5 结 论

针对传统的固壁边界处理方法中的边界力法、虚粒子法计算量大、对于复杂边界处理难以达到实时性的问题，本文提出一种对称区域边界处理方法。对于靠近边界的流体粒子，首先找到被边界截断的流体粒子的支持域，然后通过中心对称，在流体粒子支持域中找到关于被截断区域对称的区域，在计算流体粒子密度时，对这个对称区域内的粒子增大权重，避免了边界对粒子支持域截断带来的密度、压力计算错误等问题。与经典传统方法相比，该方法无需生成虚粒子，减少了计算量，在保证逼真度的前提下达到实时性，且随着粒子数的增加，该方法的耗时增长也明显比其他传统方法慢，计算效率高的优势更明显，为复杂场景的模拟奠定了良好的基础。此外，针对传统 CSF方法计算表面张力时曲率计算存在的误差，本文进行了修正，只通过边界粒子计算边界粒子的曲率，减小了计算量，提高了模拟效率，且模拟效果更好。此外，本文的对称区域边界处理方法可以推广到任意复杂边界，但边界越复杂，本文方法的计算也越复杂；但比传统的生成虚粒子的计算简单快速。

本文在基于表面粒子提取的表面张力计算中，用到余弦函数，增大了计算量，计算效率有待进一步提高。