基于原型网络的小样本图像识别方法

樊 笛,巨志勇

(上海理工大学光电信息与计算机工程学院,上海 200093)

0 引 言

近年来，在卷积神经网络和深度学习[1-4]技术的影响下，图像识别分类技术获得了长足发展，并已经被广泛应用于各个领域。卷积神经网络的多层连接结构能够捕捉到图像更深层次的特征，图像识别和分类的准确性有了质的飞跃。深度学习是一种需要海量数据训练的方法，大多数用于目标分类的深度学习网络需要非常大的数据库投入训练。但是在现实世界中，大多数目标分类问题并没有大量的标注数据，并且获取大量标注数据需要很高的成本，因此基于小样本数据集的图像分类识别是深度学习领域发展的一个重要方向。

目前针对小样本数据集的图像分类方法大致可分为2类：一类是基于传统机器学习[5-9]的分类识别算法，该类算法着重于提取图像的颜色、形状、纹理以及梯度等底层特征，并且需要解决特征协方差矩阵的不稳定性和奇异性；另一类是基于深度卷积神经网络的图像识别算法，如迁移学习(Finetune)[10]、图神经网络(Graph Neural Network)[11]和度量学习(Metric Learning)[12]等，利用卷积神经网络的多层结构将图像的底层特征抽象为高层特征，使模型具有更高效的特征学习能力。但目前的小样本图像分类算法还存在训练时间长、识别不稳定等问题。

本文在现有的度量学习模型的基础上，提出一种基于多层卷积神经网络的原型网络模型，用于小样本条件下的图像识别分类。该方法利用多层卷积神经网络构造基于原型网络的预训练模型，然后将测试集中的标注样本映射到嵌入空间，计算嵌入空间中训练集的加权平均值，将其作为类原型，然后把测试图像投影到已经训练好的模型上，根据嵌入空间中测试图像与类原型之间的欧氏距离将其归类。此方法可以从少量训练样本中快速学习特征，将测试图像正确分类，具有训练时间短、识别率高、鲁棒性强的特点。

1 原型神经网络

1.1 原型网络介绍

原型网络(Prototypical Networks)[13]的思想是：在嵌入空间中，每个类别都存在一个特殊的点，称为类的原型。利用神经网络的非线性映射将输入图像映射到嵌入空间中，此时嵌入空间中训练集的加权平均值就是类的原型。该类别中每个样本的嵌入空间表示都会围绕类原型进行聚类。预测分类的时候，将测试图像也映射到嵌入空间中，计算与训练集类别的各个类原型间的距离，即可进行分类。

原型网络将复杂的分类问题转化成了在特征向量空间中的最近邻问题，对于处理小样本数据集下的分类问题可以得到较好的效果。

1.2 深度原型网络架构

本文的深度原型神经网络的架构[14]如图1所示，分为模型预训练和分类测试2个部分。首先将训练集输入到卷积神经网络中，然后采取连续的反向传播算法和Adam优化算法来提取模型的权重参数和图像特征。测试时，将测试数据投影到嵌入空间中，计算出该类别的原型，然后将测试图像投影到嵌入空间中，计算与各个原型间的欧氏距离，将其与距离最近的类原型划为一类。

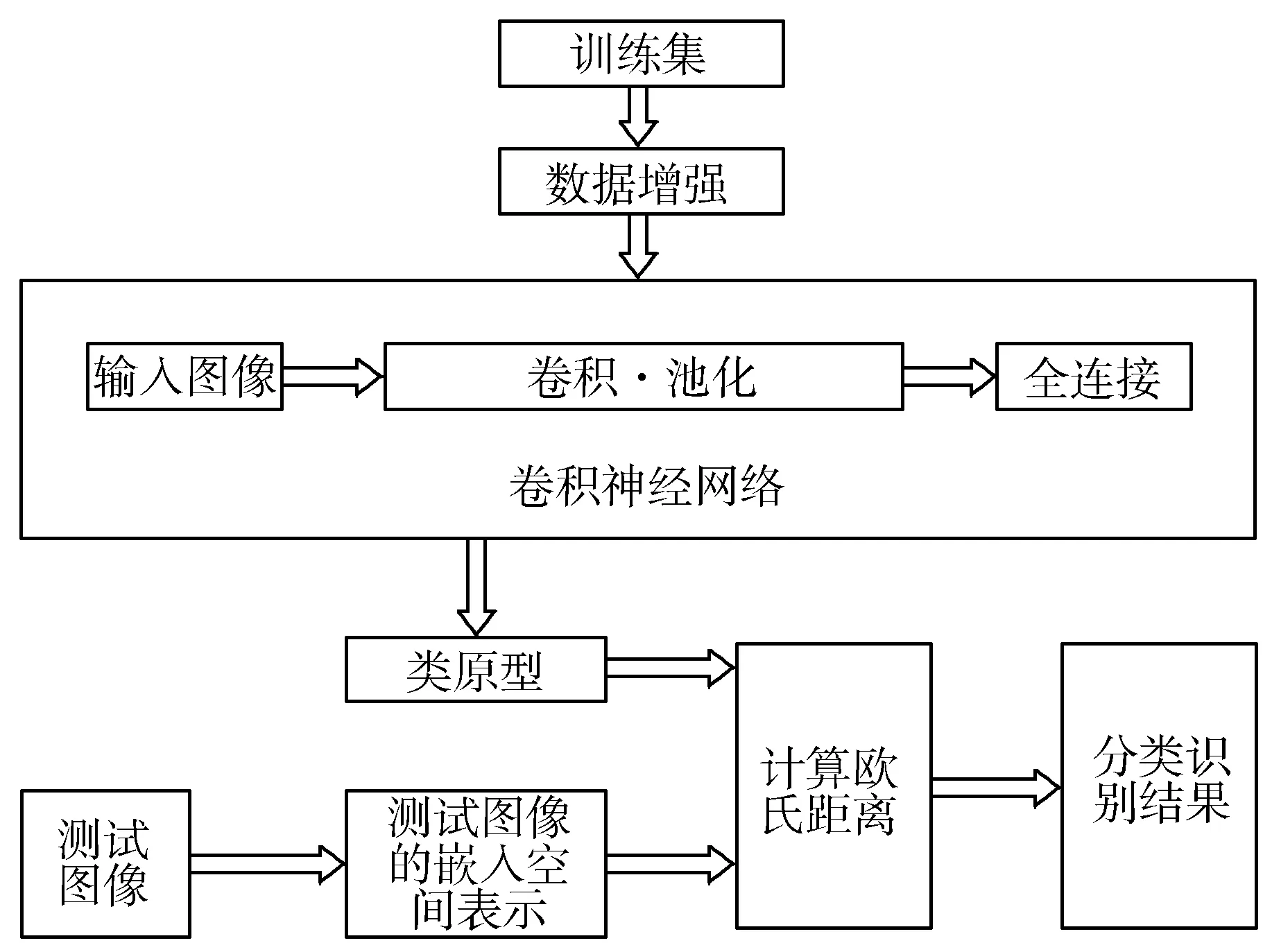
图1 系统架构图

特征提取网络如图2所示，包含4层卷积神经网络。图像输入到特征提取网络后，不同层次的卷积神经网络会提取到不同层次的特征。针对小样本数据集而言，ReLu激活函数[15]比起sigmoid和tanh等激活函数具有更好的拟合能力，可以增强网络的非线性，使之后的神经网络具有更好的判别性，所以在卷积神经网络的后面使用ReLu激活函数作为该层的神经元。第3个和第4个卷积网络层产生的结果会共同输出到全连通层。此外神经网络需要对图像的微小移动具有较强的不变性，所以在前3个卷积网络层的后面加入了max-pooling层[16]，最终特征提取网络的输出为128维的特征向量。

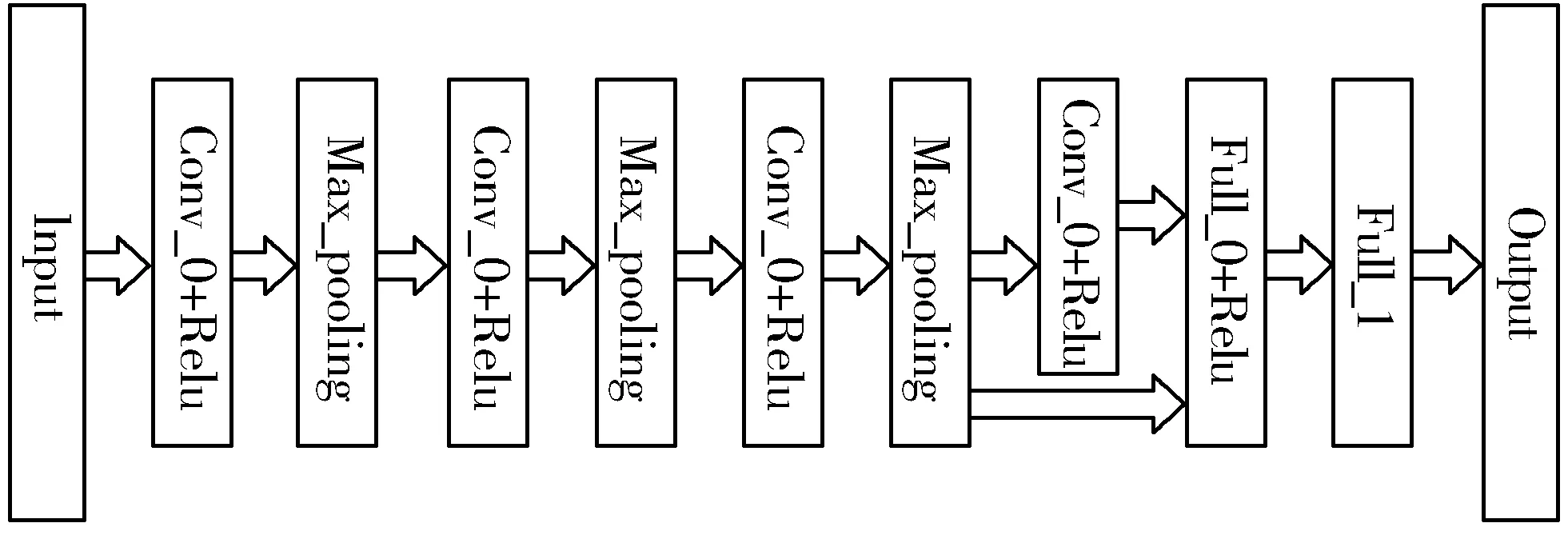
图2 神经网络结构图

所定义的网络的配置参数见表1。其中“Conv”前缀表示卷积层，“Pool”表示池化层，“Full”则表示全连接层。

表1 神经网络参数表

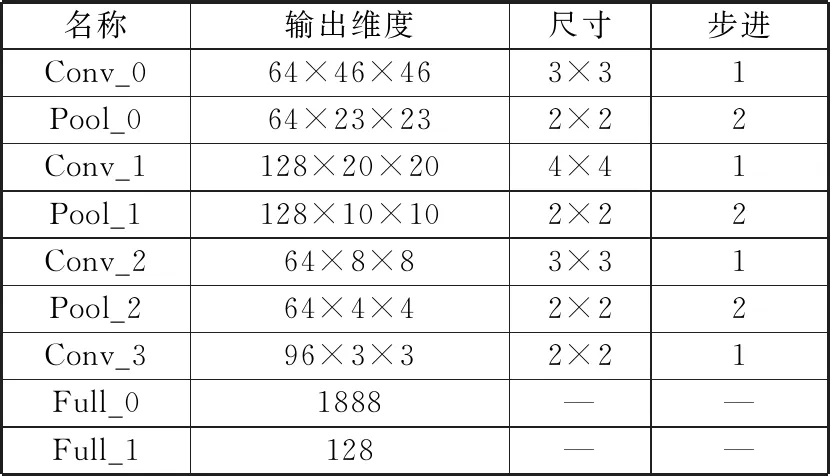
名称输出维度尺寸步进Conv_064×46×463×31Pool_064×23×232×22Conv_1128×20×204×41Pool_1128×10×102×22Conv_264×8×83×31Pool_264×4×42×22Conv_396×3×32×21Full_01888——Full_1128——

2 分类实现过程

2.1 数据增强

在样本量较少的情况下使用深度学习相关方法训练模型，识别率往往达不到预期。为了解决数据集训练样本严重不足的问题，可以利用数据增强(data augmentation)[17]方法，在原始数据集的基础上，利用各种图像变换方法增加数据样本。常见的数据增强方法包括：旋转变换、仿射变换、平移变换、尺度变换、PCA和ZCA白化等。本文采用平移变换、旋转变换、局部放大和仿射变换中的剪切变换。这样一方面保证了充分利用有限的数据集尽量多地得到相近图片，另一方面也防止了过度的图像变换导致原始图片信息畸变，保证了原始图片信息的完整性。

平移变换是将图像的所有像素坐标分别加上水平偏移量和垂直偏移量，如式(1)所示。假设x和y方向上的偏移量分别为x0和y0，则变换后的像素坐标为：

(1)

旋转变换是将原图像绕原点顺时针旋转角度∂，如式(2)所示，旋转后的像素坐标为：

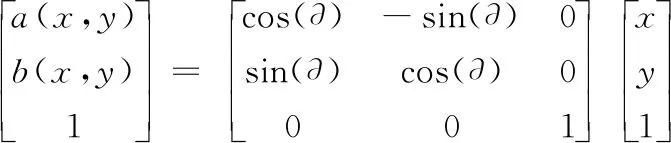
(2)

剪切变换(shear transformation)是仿射变换的一种原始变换，剪切变换可以仅是x坐标或仅是y坐标受横向剪切，也可以是2个坐标同时受横向剪切。本文为了尽可能多地保持原始图片的信息完整性，仅考虑x轴受横向剪切的情况。像素原坐标值经横向剪切后的新坐标值如式(3)所示，其中值c为剪切常数。

(3)

为了减少过拟合情况的发生，本文利用数据增强处理仅在原始小样本数据集的基础上扩充3倍。

2.2 将图像映射成嵌入向量

在图像识别问题中，如何把图像中的节点进行嵌入变成可计算的值或者向量，一直是当前研究所关注的问题。这需要充分利用节点在网络中的拓扑关系[18]，给出节点的隐含向量表示，从而将离散空间中的网络节点嵌入到高维空间中。

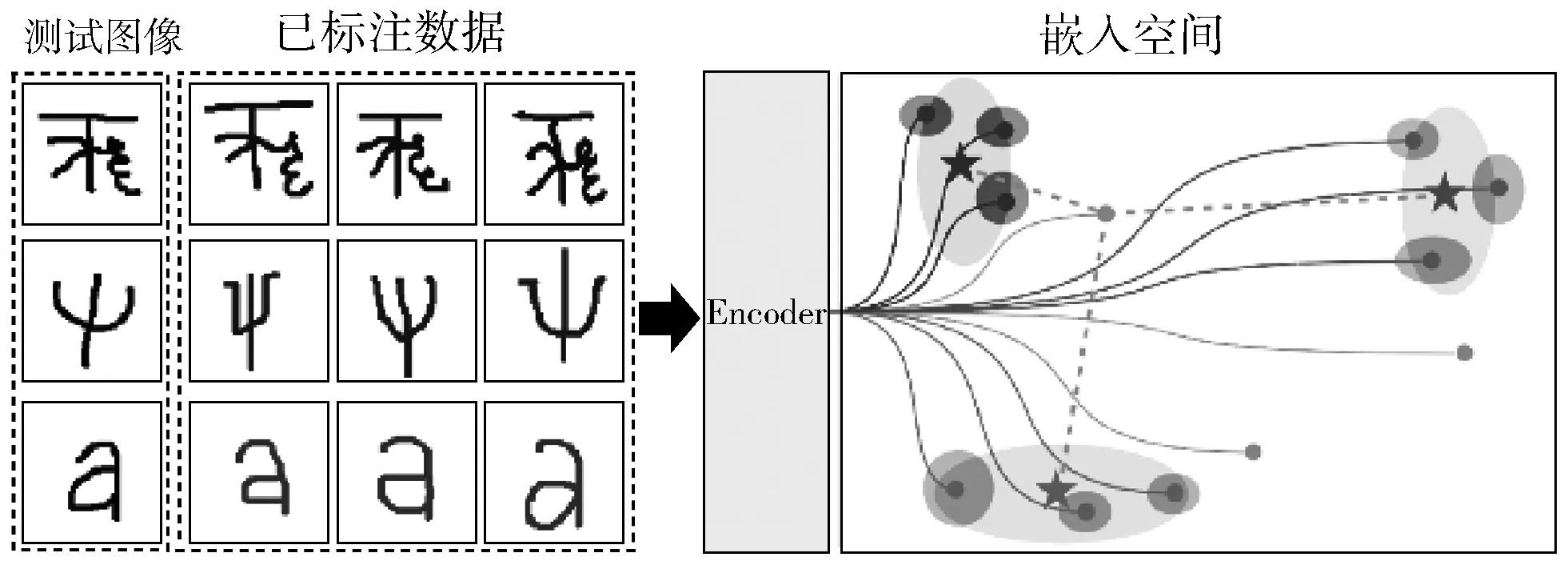
图3 神经网络映射关系

图3中，神经网络将图像映射到嵌入空间中，已标注样本图像用于定义特定类的原型。图中虚线表示嵌入空间中测试图像与各个类原型之间的距离。

本文使用一个多层卷积神经网络，将图像编码成多维的欧氏向量映射到嵌入空间中。假设S={(X1,y1),…,(XN,yN)}是一组小样本的N标签的数据集，其中，X是输入数据的向量化表示，y为其对应类别，Sk则表示类别为k的数据集合。在原型网络中，fθ是一个映射函数，它接受图像I并将其转换为向量X。

fθ:I∈RH×W×C→X∈RD

(4)

式(4)中，H和W为输入图像的高度和宽度，C为其通道数，D是嵌入空间的维数，θ是可训练神经网络的权重参数。

2.3 定义类原型

在嵌入空间中，每个类别都存在一个特殊的点，称为类的原型(class prototype)。为了获得图像的高层特征，需要利用神经网络的非线性映射将输入图像映射到嵌入空间中，此时嵌入空间中训练集的加权平均值就是类的原型。该类别中每个样本的嵌入空间表示都会围绕类原型进行聚类[19]。预测分类的时候，将测试图像也映射到嵌入空间中，计算与训练集类别的各个类原型间的距离，即可进行分类[20]。

编码器将图形映射到嵌入空间后，每个图像都会生成一个协方差矩阵，各个训练图像的嵌入向量进行加权线性组合，对特定类的训练图像产生的协方差矩阵进行聚类，定义类原型ck：

(5)

2.4 计算测试点到类原型的距离

原型网络将样本映射到一个高维嵌入空间，在这个空间中，同类样本之间的距离较近，异类样本之间的距离较远。每个类别都存在一个聚在某单个原型表达周围的特征向量，该类的原型是训练集在特征向量空间中的均值，然后通过计算嵌入空间中测试图像和每个类别的原型表达的距离就可以进行分类。原型网络将复杂的分类问题转化成了在特征向量空间中的最近邻问题。

原型网络能够在嵌入空间中学习类和方向相关距离度量，训练的速度和准确性在很大程度上取决于如何使用距离来构造损失，大量的实践后，本文选择使用线性欧几里得距离来计算嵌入空间中类原型ck到测试点xi的距离dk(i)：

(6)

(7)

其中，Mk是类k的协方差矩阵的逆矩阵。

2.5 目标函数的定义

为了对原型神经网络进行训练，需要定义一个可微分的目标函数[21]。本网络的整体目标是要学习一个可以正确分类图像类别的神经网络，此目标函数需要有2个重要条件，即图像原型的能够正确表述该类特征和合适的分类函数。本文使用Softmax回归函数作为图像类别的分类函数，得到测试点x属于类别k的概率：

(8)

原型神经网络的目标函数可以定义为：

(9)

由此可以计算出测试点到各个类原型的距离，将测试点与最小距离所对应的类原型划分为一类。

3 测试与结果

3.1 数据集设置

为了验证识别算法的有效性，本文在国际上常用的Omniglot数据集和miniImageNet数据集上分别进行分类识别实验，保证训练集和测试集相互独立，没有交集。

Omniglot数据集包含1632个种类的字符集合，其中每个种类都包含20个黑白的105×105像素的手写体字符。本文随机选取其中1200个种类，并从每个类中随机选择15张图像作为训练集，每类剩下的5张图像作为测试集。

miniImageNet数据集共有100个种类的图像集合，其中每个种类都包含600张84×84像素的彩色图像。本文从中随机选取50个种类，并从每个种类中取60张图像作为训练集，取20张图像作为测试集。

本文将实验所需图像大小都处理为48×48像素，以加快训练速度，并且通过数据增强处理，将训练集扩充为原来的4倍。

3.2 模型训练及准确率

本文在训练时采用Adam[22]方法对神经网络进行优化，学习率设置为0.001。Adam方法在训练的过程中能够自适应地调整各个参数的学习率，较快地收敛，并且对于数据比较稀疏的情况具有较好的适应性。

本文使用测试精度(Test Accuracy)以及过拟合率(Overfitting Ratio)来作为模型评价标准。其中，测试精度的定义为：

(10)

式中，CorrectTestImages表示验证正确的测试集图像数量，TestImages表示测试集图像的总数，测试精度值越大，模型识别效果越好。

过拟合率的定义为：

(11)

式中，TrainAcc表示训练精度。过拟合率越接近1，神经网络的抗过拟合能力就越强。

3.3 实验结果分析

为了保证算法能提取足够的特征，实验在Omniglot数据集和miniImageNet数据集上各迭代运行50次，由此可以反映出算法学习特征的过程。然后分别统计模型在Omniglot数据集和miniImageNet数据集上的识别准确率，并与迁移学习(Finetune)、匹配网络(Matching Network)和图神经网络(GNN)识别算法进行比较，如表2和图4～图6所示。

表2 模型测试准确率统计/%

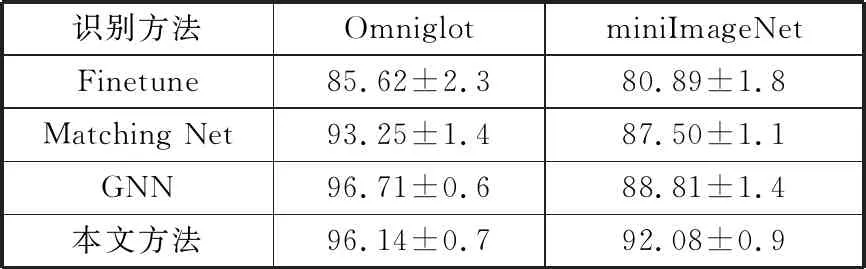
识别方法OmniglotminiImageNetFinetune85.62±2.380.89±1.8Matching Net93.25±1.487.50±1.1GNN96.71±0.688.81±1.4本文方法96.14±0.792.08±0.9

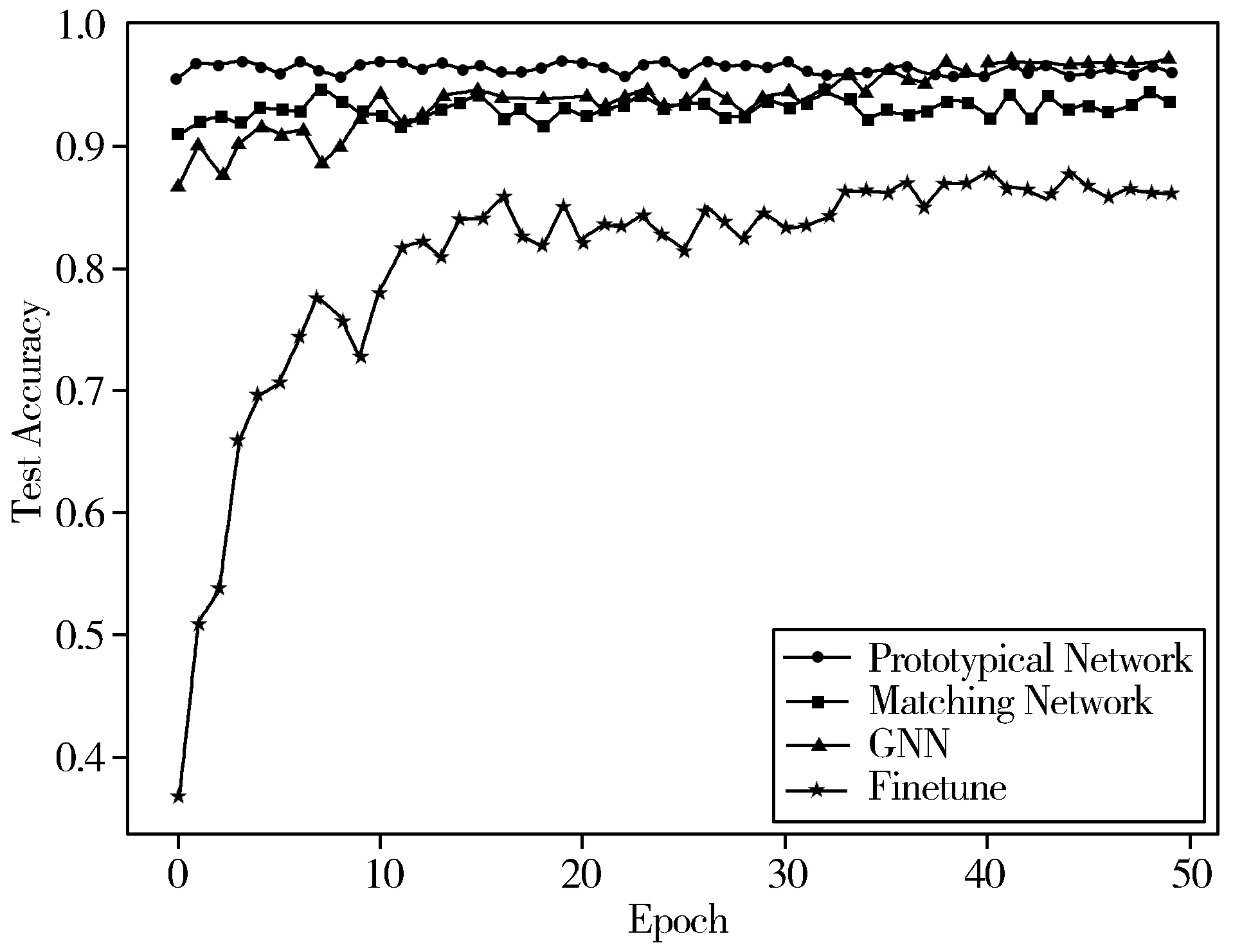
图4 Omniglot数据集上的测试精度

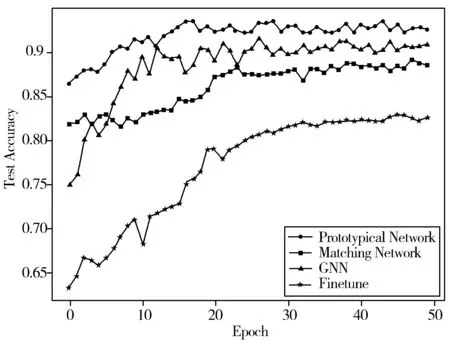
图5 miniImageNet数据集上的测试精度

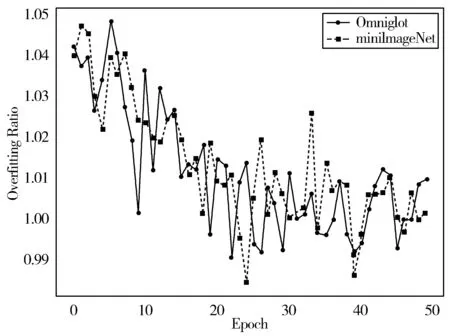
图6 本文方法的过拟合率

结合表2和图4、图5可以看出，在大规模数据集环境中识别结果较好的模型Finetune在小样本环境下，随着训练次数的增加，模型的识别率缓慢趋于收敛，但与原型网络、匹配网络和图神经网络方法相比仍然较低。本文的原型网络以全连接层作为承接枢纽时，获得了源训练模型的参数和经验，提高了卷积神经网络的特征表达能力，仅经过少量训练即可获得较高的识别准确率，针对小样本复杂图像分类，也能取得较好的分类效果。从图6中可以看出，模型在Omniglot数据集和miniImageNet数据集上的过拟合比率都稳定在0.98～1.05之间，这说明本文实验的训练过程中有效避免了过拟合问题的出现。

总之，在小样本实验条件下，本文方法具有较快的训练速度、较高的准确率和较强的鲁棒性。

4 结束语

本文构建了一个基于原型网络的卷积神经网络分类器，用于小样本数据集条件下的图像识别分类。使用平移变换和剪切变换等数据增强方式扩充数据集，利用多层卷积神经网络将非线性的输入图像映射到嵌入空间中，将复杂的分类问题转化成了在特征向量空间中的最近邻问题。与目前存在的其他小样本图像识别方法相比，此方法具有简洁高效、训练时间短、识别率高的特点。进一步的研究工作可以在本文基础上加入多示例学习算法，以提高对小样本复杂彩色图像的识别准确率。