基于网格搜索与交叉验证的SVR血压预测

奚杏杏，刘宇红，张荣芬

(贵州大学大数据与信息工程学院，贵州 贵阳 550025)

0 引 言

随着人们生活水平的提高，高血压的患病率和患病人数都呈持续攀升的趋势[1]，患病初期，可能不会有明显的症状，但随着病情的发展后期可能会引发冠心病、糖尿病等多种并发症[2-3]。

目前对于人体血压分析预测的回归模型主要有Logistic线性回归[4]、Lasso回归、神经网络以及支持向量机回归[5]等。Sideris等人[6]利用递归的神经网络模型对人体血压进行预测，预测准确度较高但训练速度过慢，在实时处理方面性能较差。Hsieh等人[7]通过对脉搏波的传导时间建立线性回归模型进行血压预测，真实值与预测值之间的相关系数很高，但预测准确度较低，尤其是对高压的预测仍需进一步完善。国内，朱海龙等人[8]将自回归移动平均模型与支持向量机模型相结合，利用粒子群优化算法进行参数寻优，预测精度较高，但不能反映各种生理参数之间的相互关系。赵谞博等人[9]通过支持向量回归的血压预测算法实现高压的预测准确率超过53.93%，低压的预测准确率超过75%，虽然相对其他机器学习算法而言体现出很大的优势，但无论在算法改进、性能提升方面，还是在有效整合人体生理参数建立血压预测模型等方面，都还有很大的研究空间。

通过3.3节参数寻优可知核函数系数及惩罚因子对于支持向量回归模型的预测效果具有相当重要的作用，而利用网格搜索与交叉验证相结合能更加准确便捷地寻找出最优的参数对。因此，本文在以径向基函数作为核函数[10-11]的基础上通过网格搜索与交叉验证相结合的方式提高人体血压模型的预测性能。利用支持向量回归原理，以心率和血氧作为主要研究对象，使用MIMIC-II数据库[12]的数据，建立心率、血氧与血压之间的SVR回归模型，并通过准确率及均方根误差这2个评价指标进行估测。结果表明对高压和低压的预测准确率约为71.39%、81.69%，具有一定的高效性和应用潜能。

1 SVR原理及技术简介

1.1 SVR回归原理

支持向量机是在分类与回归分析[13]中用于对数据进行分析的监督式学习模型(主要分为训练模型和预测模型[14])，除了可以进行线性分类，还可以进行非线性分类[15]。对于线性的支持向量机，主要通过寻找超平面[16]对特征样本进行分类。而对于非线性的支持向量机，需要把数据映射到一个维数比原空间高的新的特征空间中，并在新的特征空间使用线性的支持向量机进行特征分类。为了避免内积运算计算量过大，在进行特征选择时，需要通过核函数在变换空间直接计算内积使其与原空间中的内积计算直接对应。

本文使用径向基函数作为核函数[17]，采用非线性数据。因此需要先通过特征选择将特征空间x=(HR,SpO2)的非线性数据集映射到一个更高维度的新特征空间X=(x1,x2,…,xn)，并在这个新的特征空间中使用线性的支持向量机来构建人体生理参数与血压之间的非线性映射模型。

已知训练集T={(xi,yi),i=1,2,…,k}，满足xi∈RN，yi∈R，xi、yi为一般情况下支持向量机的映射关系，得回归方程为：

F(x)=WTΦ(x)+b

(1)

其中，W为F中的一个向量，Φ(x)为：

(2)

其中，C为惩罚因子。考虑约束条件，引入拉格朗日算子α、α*、β、β*，将最优化问题转化为对偶问题[18]，重新规划拉格朗日方程：

(3)

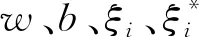
(4)

(5)

(6)

(7)

(8)

将上述式子代入J函数并化简得到：

(9)

当使用核函数K(xi,xj)时，上式变为

(10)

(11)

其中，核函数K(xi,xj)的表达式为:

K(xi,xj)=exp (g‖xi-xj‖2)

(12)

式中，g即为核函数的系数(gamma)。

1.2 交叉验证与网格搜索

交叉验证主要分为K折交叉验证、Holdout验证、留一验证，其目的是为了让模型评估更加准确可信。本文使用的是K折交叉验证，所谓K折交叉验证指在训练过程中将训练集划分为K个小的子集，每次迭代时都将其中的一个子集作为测试集，剩余K-1个子集作为训练集。经验证v=10时学习效果较好[19]，故以10折交叉验证为例简要介绍其步骤。首先将数据集划分为不相交的10个子集，每次挑选其中1个子集作为测试集，其余9个子集作为训练集对模型进行训练得到模型指标；重复上述步骤10次使得每个子集都作为一次测试集分别得到10个模型指标；取10个模型指标的平均值作为10折交叉验证最终的模型指标。其对应的详解图如图1所示。

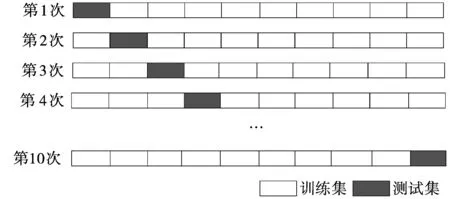
图1 交叉验证详解图

网格搜索是指在特定的空间范围内将g和C构成的参数空间划分为若干长短相同的网格，网格中每个点都代表一对参数，依次遍历网格中的每一个点并计算其对应模型的均方误差值，最后通过对比找出使得均方误差值最小的一对参数即为最优参数对[20]。

2 评价指标

2.1 准确率

准确率(accuracy)是指对于给定的数据集，分类正确的样本个数与总的样本数的比值，代表模型的整体准度，数值越大代表模型越准确。对于SVR模型其准确率可以通过表1的混淆矩阵求出。

表1 混淆矩阵

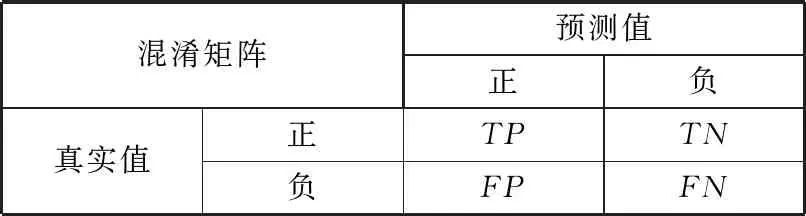
混淆矩阵预测值正负真实值正TPTN负FPFN

则准确率为：

(13)

2.2 均方根误差

由式(14)的表达式可知，均方根误差(RMSE)指预测值与真实值之间偏差的平方和比上样本的总个数再对其取平方根，因此RMSE可以用来评价预测值与真实值之间偏差的大小，并且RMSE值越小代表模型预测性能越好。

(14)

3 实验结果与分析

3.1 实验条件及过程

本文使用LIBSVM工具箱，在GPU的PyCharm环境下选择Python编译器开展实验。实验前需先将采集到的数据进行一系列的预处理，随后利用Python编译器将分类函数与预测函数编译为PyCharm可识别的文件，通过分析心率、血氧与血压之间的隐含关系构建训练模型，再根据网格搜索与交叉验证寻找使系统性能最好的g和C值，并将测试数据集输入到最优参数下的SVR模型中得到相应的血压预测结果，最后将本文得到的预测结果与使用其他经典机器学习算法得到的预测结果进行对比评估。对应的实验流程图如图2所示。

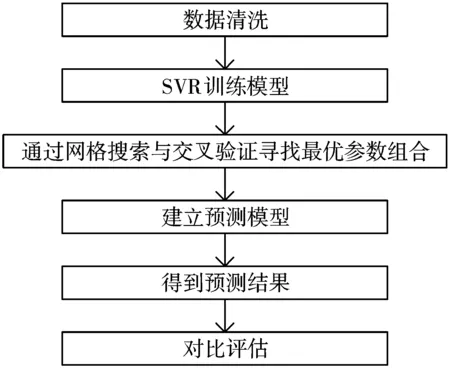
图2 实验流程图

3.2 数据准备

3.2.1 数据介绍

本次实验的数据来自MIMIC-II(http://mimic.physionet.org/)数据库。MIMIC-II数据库包含了大量通过监测器收集到的人体生理数据[21]。本次实验随机抽取了不同性别、不同年龄段、不同监测器、不同时间段共33969条特征数据，其中27030组数据用来训练SVR模型，剩余的6939组数据则用来对模型进行测试。

3.2.2 数据预处理

1)缺失值、异常值处理。在实际的采集数据中，样本可能会由于采样率发生变化、数据丢失或者是录入错误等原因，造成一个或多个数据的缺失或异常。本文对于少量的缺失值采用平均值进行替换，而缺失较多的数据则直接删除。剔除不合理的记录、有效数据长度不足48 h的数据、病危病人和数据记录中丢失的数据长度超过4 h的记录以及不同时具有心率、血氧和血压的病人数据。

2)标准化处理。对于采集到的特征数据值，可能会参差不齐，存在一些数值很小或很大的数据，或者是数据分布得过于分散，都可能会误导模型的正确训练。因此在进行模型的训练之前需要先对特征值进行标准化。所谓数据标准化就是将所有的数据转换为均值为0，方差为1的正态分布。本文采用StandardScaler()方法进行规范化，公式如式(15)所示

(15)

其中，x为特征值，μ为均值，σ为标准差。

3.3 参数寻优

由1.1节原理中g及C的表达式可知，g和C均会对SVR的性能产生很大影响。对于g，取值过大会造成核函数只作用于支持向量样本附近，导致泛化能力下降；取值过小，可能会引起平滑效应过大。惩罚因子则表示对分错的点加入多少的惩罚。取值很大几乎趋于无穷时，表示几乎不存在分错的点，会出现过拟合现象；取值过小并趋于0时，表示分错的点很多，容易出现欠拟合。

本文使用“网格搜索”[22]与“交叉验证”[23]相结合的方式来寻找最优参数对。具体步骤如下：

1)确定g和C的取值范围均为[2-8,28]。

2)在取值范围内将网格等距离划分为10份，获得一个10×10的粗网格[24]。

3)计算网格中第一个点所对应的参数对经过10折交叉验证后的均方误差值，然后将这10个均方误差值的平均值作为此点的均方误差值(MSE)。

4)设定最小均方误差为0.5，遍历网格中所有的点重复步骤3计算出对应的MSE，并与设定值比较，若某个点的MSE小于0.5则记录该组参数，否则以该点为中心重新构造一个10×10的细网格，并返回步骤3。

5)重复以上步骤，找出最佳参数对。

通过上述的寻优步骤，得到如图3所示的参数寻优结果图。由图可知当C=1.0，g=34时，其对应的均方误差值最小约为0.2861。

图3 参数寻优结果图

3.4 预测实验及结果

为验证算法的性能，本文开展了相应的血压预测对比实验，将几种现有的常用回归模型进行比较，分别为改进前的SVR模型、前述的人工神经网络、线性Logistic回归以及Lasso回归模型，并利用准确率及均方根误差这2个评价指标对模型进行性能评估。

3.4.1 准确率对比实验及结果分析

通过预测实验得到本文基于网格搜索与交叉验证的SVR回归(K-SVR)、改进前的SVR模型(SVR)、Logistic回归、人工神经网络(ANN)和Lasso回归对于人体高压和低压预测的准确度如图4所示，其中L代表对于低压的预测准确率，H代表对于高压的预测准确率。

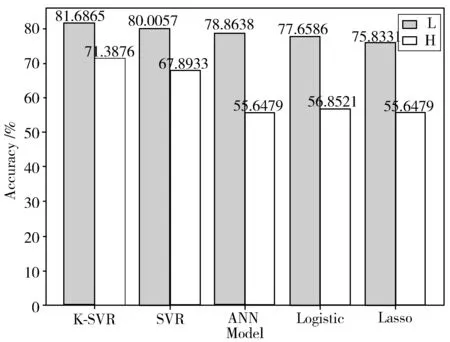
图4 不同模型准确率对比图

由图4可知，本文模型对低压的预测准确率超过了81%，对于高压的预测准确率超过了71%，均明显高于其余4种算法的预测准确率。表明在准确率方面，本文提出的基于网格搜索和交叉验证的SVR模型对于高压和低压都有更好的预测性能。

3.4.2 均方根误差对比实验及结果分析

表2是几种不同算法对于高压和低压预测的均方根误差值的结果对比图。由表格可知人工神经网络、Logistic线性回归以及Lasso回归对于高压预测的均方根误差值均高于0.6，而本文改进后的SVR算法预测高压的均方根误差值约为0.53，明显低于其余4种算法。而对于低压预测的均方根误差值约为0.42，也明显低于其余4种算法的均方根误差值。因此在均方根误差方面，本文改进的SVR回归模型在对血压进行预测时表现出了更低的误差率。

表2 各算法预测血压的均方根误差

血压K-SVRSVRANNLogisticLasso高压0.53490.57290.66600.65690.6549低压0.42790.44710.49160.47270.4835

总体而言，本文改进的SVR模型，在利用心率和血氧实现对人体血压的预测时，不管是在准确率方面还是在均方根误差方面，均明显优于其余4种现有的常用回归模型，取得了较好的效果。

4 结束语

本文采用麻省理工学院的MIMIC-II数据库的心率、血氧及血压数据，研究基于网格搜索及交叉验证的SVR血压预测模型。实验对比结果得出，改进后的SVR算法对于高压预测的准确率超过71%，对于低压预测的准确率超过81%，均明显高于其余4种对比预测模型；在均方根误差方面高压的值约为0.53，低压的值约为0.42，也均明显低于其余4种算法；表明本文提出的基于网格搜索与交叉验证的SVR算法相较于其他4种对比的机器学习模型算法而言对于人体血压有更好的预测性能。