煤矿安全状态的变权理论评价模型及其工程应用
李希建,华攸金,陈刘瑜
(1.贵州大学 矿业学院,贵州 贵阳 550025;2.复杂地质矿山开采安全技术工程中心,贵州 贵阳 550025;3.贵州大学 瓦斯防治与煤层气开发研究所,贵州 贵阳 550025)
煤炭行业作为我国重要的传统能源支柱产业,在经济发展新形势下,其行业发展形式也发生了重大变化,以安全生产、环境保护为特征的科学开采成为煤炭行业发展的趋势[1]。煤矿全面进入深部开采阶段,由于地质构造复杂,瓦斯浓度高,煤与瓦斯突出和冲击地压等灾害因素影响,使得煤炭行业的安全生产形势较为复杂。因此,有必要对煤矿的安全状态进行阶段性评价,进而提高煤矿的本质安全化程度,实现煤炭行业健康稳定发展。
随着科学技术及理论的发展,概率评价法、模糊评价法、层次分析法、灰色理论分析法、神经网络评价法[2-6]等方法被广泛应用于煤矿安全综合评价,并取得了丰富的研究成果,但这些理论在安全评价过程中容易忽略指标内部差异性对评价结果的影响,且其客观性及可操作性需进一步完善。变权理论是由汪培庄于20世纪80年代提出的一种动态模型方法,采用变权基本原理修正权重,以应对常权权重导致实际决策结果偏向极端的情况,同时强调指标权重应随指标取值状态的变化而变化[7];李洪兴结合因素空间理论的基本原理对变权理论进行系统的研究,讨论了状态变权向量与均衡函数之间的关系,使得变权理论更趋于完善[8];李博等[9]构建了基于变权理论的煤层底板突水预测评价模型,取得了较为理想的结果;王洪德等[10]将变权理论引入围岩稳定性评价领域,进一步提高了评价的可操作性和准确性。在对评价对象安全综合评价过程中,指标权重及关联度的确定对综合评价结果的准确性至关重要。通常使用常权或一些简单的关联函数计算权重,但缺乏评价对象在评价体系中的动态参与;采用最大隶属度准则进行安全等级评价容易损失信息,导致评判结果产生偏差。
鉴于此,笔者在运用物元可拓方法对煤矿安全状态进行综合评判的基础上,引用变权理论确定指标权重,并采用贴近度替代最大隶属度准则构建基于变权物元可拓的煤矿安全状态评价模型。利用该模型对煤矿安全状态进行综合评判,以提高煤矿安全状态评价结果的准确性。
1 变权物元可拓模型
1.1 确定经典域、节域及物元矩阵
假定待评价对象为n个评价指标、m个评价等级的变权物元,则经典域物元Rj表示为:
(1)
式中:i为评价指标个数,i=1,2,…,n;Nj为第j个评价等级,j=1,2,…,m;Vij是Nj对应Ci的取值范围,即为经典域;Ci为第i个评价指标;Vnj是Nj对应Cn的量值范围;anj和bnj分别为Vnj的上下限。
节域物元Rp表示为:
(2)
式中:Np为安全等级p的待评对象,p=1,2,…,m;Vpi是Np对应Ci的取值范围,即为节域;Vpn是Np对应Cn的量值范围;apn和bpn分别为Vpn的上下限。
待评物元矩阵如下:
(3)
式中:R0为待评物元;Ci表示N0的n个特征;Vi是N0对应Ci的实际值。
1.2 规格化处理
为了统一指标量纲差异性,对经典域物元Rj,待评物元R0进行规格化处理,可得:
(4)
(5)
1.3 变权理论确立各评价指标权重
为了减少指标权重确定过程中的主观因素影响,突显各评价指标的均衡性及体现评价对象在综合评价中的动态参与,采用传统的层次分析法初步确定评价指标权重,同时结合变权理论进行初始权重修正,实现常权权重变权化,以更加贴切地反映各评价指标对待评物元的影响程度。
基于因素空间理论的变权综合模型,设常权变量W=(w1,w2,…,wn),状态变权向量S(X)=(S1(X),S2(X),…,Sn(X)),给出了由因素常权变量W和状态变权向量S(X)的Hadamard乘积确定变权向量wi(X)的方法[8],计算公式为:
(6)
Si(X)=eα(dimax-dimin)
(7)
式中:wi表示常权权重;dimax=max[|vi-api|,|bpi-vi|];dimin=min[|vi-api|,|bpi-vi|];α为变权因子,为了确保各指标具有一定的均衡性,本文取α=-1。
1.4 贴近度计算
采用最大隶属度准则进行安全等级评定,无法客观反映待评价对象自身临界区间的模糊性,容易损失信息,使得评定结果偏离实际[11]。笔者采用贴近度替代最大隶属度准则计算得出评价物元与各级集合的符合程度,贴近度计算公式为:
(8)
式中:N表示贴近度;D表示距离。
待评物元的贴近度公式为:
(9)
(10)
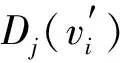
1.5 等级评判
由Nj′(p0)=max[Nj(p0)]计算知,待评物元属于j′级(贴近度最大)。令:
(11)
(12)
式中j*为待评物元的等级变量特征值,表示评价对象与该等级集合的符合程度,同时指示偏向邻近等级的程度。
2 实例应用
2.1 煤矿安全评价指标体系
为验证基于变权理论模型的煤矿安全状态评价方法的可行性和有效性,笔者依据文献[12-13]中河南义马煤矿样本采集数据为例进行实例分析。煤矿安全状态指标体系包括人员三违章C1、月平均培训时间C2、平均工作年龄C3、提升设施完好率C4、运输设施完好率C5、机电设施完好率C6、通风设施完好率C7、排水设施完好率C8、消防设施完好率C9、煤层倾角C10、矿井涌水量C11、煤层最短自然发火期C12、顶底板稳定性C13、粉尘最大浓度C14、万吨瓦斯突出次数C15、安全制度完善率C16、安全措施完善率C17、安全管理时效性C18、安全管理有效率C19、应急机制完善率C20等20项指标[12]。根据常用分级标准、专家经验及矿井安全生产的特点,将矿井的安全等级分为Ⅰ级(安全)、Ⅱ级(较安全)、Ⅲ级(一般)、Ⅳ级(较不安全)及Ⅴ级(不安全)。各评价指标的安全等级临界值参考文献[13-14]确定,煤矿评价指标风险等级分界值及样本数值如表1所示。
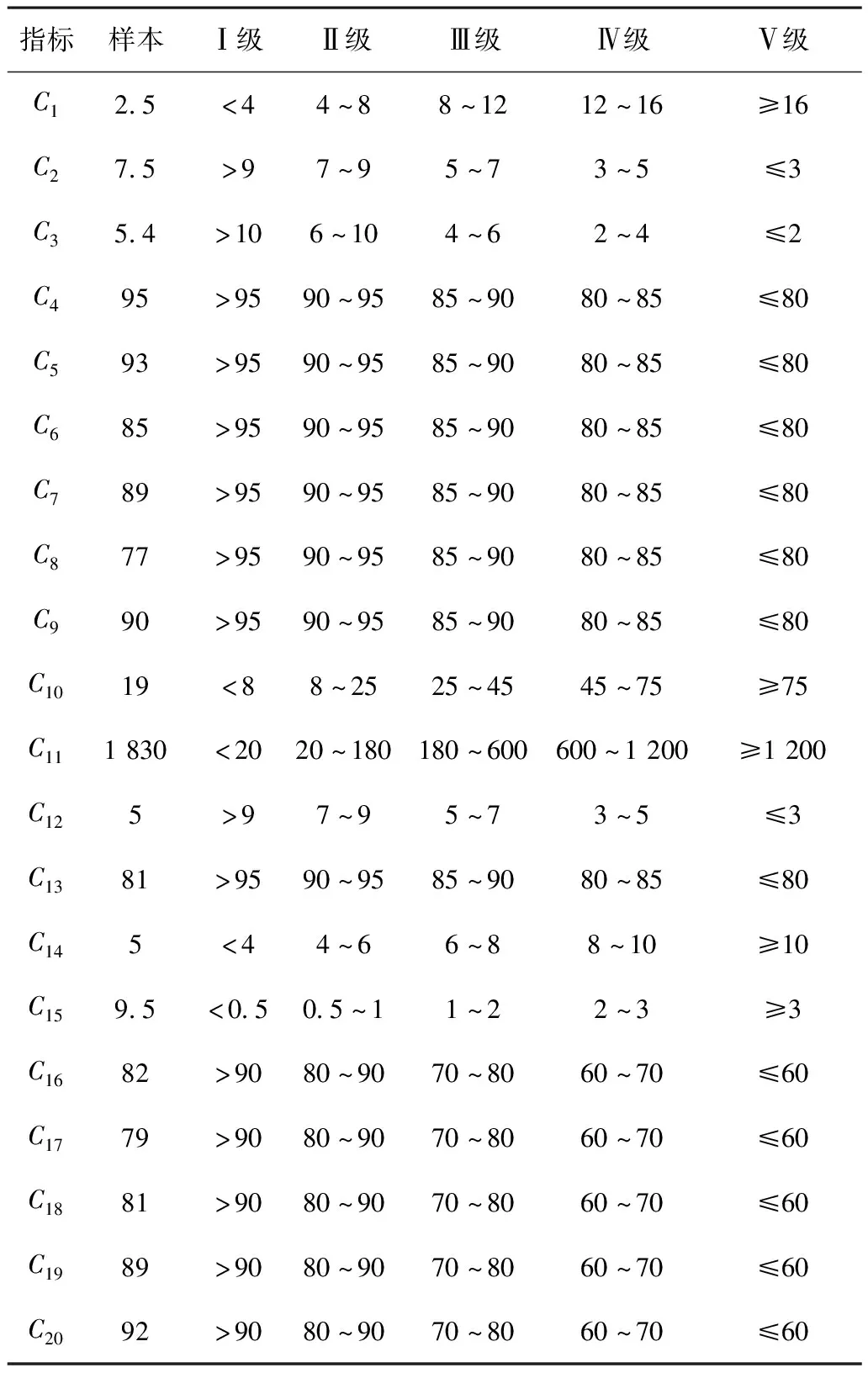
表1 煤矿评价指标样本数值及风险等级分级标准
2.2 权重的确定
由于各指标量纲和大小不同,利用式(4)和(5)分别对经典域物元及待评样本指标进行规格化处理。根据式(6)和(7),结合运用变权理论及Matlab软件计算各指标权重。指标权重的确定应考虑不失系统性和一般性,笔者分别采用层次分析法、熵权法及变权法计算各指标权重,其中,层次分析法和熵权法的权重计算过程分别参照文献[12]和文献[15],3种方法计算权重结果如图1所示。

图1 3种方法权重计算结果
由图1可知,3种方法求得的权重总体差异不大,而当环境状态信息表现异常时,熵权法求得的权重较大,例如C11和C15。由于熵权法计算的权重与指标的取值有关,而变权法运用变权理论对各评价指标权重进行修正,从而导致3种方法计算的权重不同。对3种方法分析可知,熵权法对异常状态信息有高度敏感性,但无法保证评价结果精度;经过比较分析,变权法对异常指标作用不会进一步放大,可以减弱异常指标对煤矿安全状态评价的影响,能更有效地反映煤矿真实的安全状态,可提高评价结果的准确性。
2.3 贴近度及等级变量特征值计算
依据式(9)和式(10)计算可得评价物元与各风险等级集合的隶属程度;根据式(11)和式(12)得出评价物元等级变量特征值为2.37。3种权重确定方法所求的等级变量特征值符合:2.00 表2 贴近度和等级变量特征值计算结果 敏感性分析是指从众多不确定性指标中找出对权重和等级变量特征值有重要影响的敏感性因素,并分析其对评价对象影响的变化规律,进而判断评价对象承担风险的能力。当评价指标的实测值按照±10%、±20%、±30%、±40%的趋势变化时,分析指标权重及等级变量特征值的变化情况,并研究所建模型对指标变化的敏感性。变化情况如图2~4 所示。 图2 评价指标权重随单指标值的变化规律 (a)整体图 (b)隐藏C2指标的局部放大图 图4 j*随指标共同取值的变化规律 由图2可知,整体评价指标权重随着指标实测值的变化而逐渐变化,其中指标C2、C3、C7、C9、C18的权重值变化幅度较大。C1、C14的权重值变化规律基本一致,随着指标实测值变大而增大、变小而减小;C11和C15的权重值随着指标实测值变大而有所减小,变小而增大;指标实测值变大时,C10的权重值几乎不变,而指标实测值变小时其权重值减小。通过上述分析可知,权重随指标值变动呈现出不同的变化规律,体现了各指标在等级评价过程中的动态参与。其中,指标C2的变化趋势最为典型,权重随C2实测值变化而出现显著变化,表明其对权重结果的敏感性。 由图3可知,整体评判等级变量特征值j*变化幅度较小,其范围为2.27~2.45,这表明各指标实测值的变化不会改变煤矿安全状态评价的等级及其偏向安全等级的程度;当C2的实测值变小时,等级变量特征值j*变化范围较大。到-40%点时,j*值已大于2.50,这表明,随着C2实测值的变小,尽管煤矿安全等级不变,但安全等级逐渐偏向一般等级。其余指标值的变化对安全评价结果影响较小。由上述分析可知,C2是该评价对象的敏感性指标,因此,可加强对员工进行教育培训,以实现对敏感环节的及时排查。 由图4可知,等级变量特征值j*随各指标值的共同变大而逐渐减小,随各指标值的共同变小而增大。 综上所述,通过敏感性分析可以得出指标权重及等级变量特征值随指标变动的变化规律,一定程度上弥补了以往评价方法的不足,可为煤矿综合安全评估提供更多可靠性信息,进而提高评价结果的准确性。 1)基于变权理论和物元可拓方法建立煤矿安全状态评价模型,引入变权理论修正指标权重,可减少人为因素对安全评价结果的影响,突出评价指标的均衡性;采用贴近度来表征评价物元隶属于等级集合程度,相比于最大隶属度评判结果更贴近实际。 2)评价结果表明,利用该模型评价得出河南义马煤矿的安全状态等级为Ⅱ级,同时根据指标敏感性分析,得出员工的月平均培训时间C2是影响该煤矿安全状态的敏感性指标。 3)变权理论评价方法也适用于其他领域的相关评判工作,结合待评对象的特点,对该评价方法加以改进和优化,可以为其他评估问题提供更多可靠的信息预判,提高评价结果的准确性。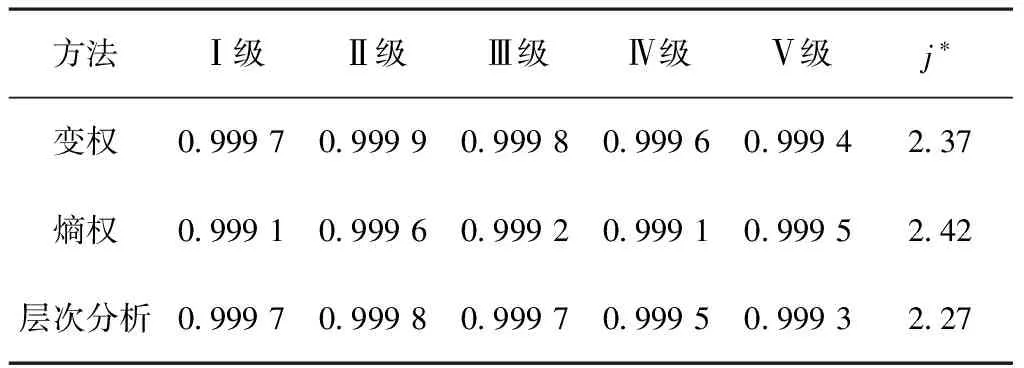
2.4 敏感性分析




3 结论

