尾矿坝倾斜抬升超载安全度试验与数值模拟研究
梁 冰,周克林,金佳旭,孙本通,魏永清
(辽宁工程技术大学 a.力学与工程学院;b.土木工程学院;c.矿业学院,辽宁 阜新 123000)
矿产资源是一种必不可少的资源,在我国经济建设中发挥着重要作用。矿产资源在开发利用的同时附带产出了大量的尾矿砂,修建尾矿坝是安全解决尾矿砂堆存的重要手段[1-3]。近年尾矿坝地质灾害事故频发,统计数据显示:全球约18 500座尾矿库中有接近220座发生过尾矿坝事故,约1.2%的尾矿库发生尾矿坝事故,而2000年以后发生的尾矿库事故中约74%的尾矿坝事故属于重大事故或超级重大事故[4-5]。
研究尾矿坝稳定性对预防尾矿坝事故具有重要意义,众多学者进行了大量的超载安全度研究[6-8]。黎保琨[9]基于坝基软弱夹层对重力坝的不利影响,开展了坝基含软弱夹层重力坝的超载模型试验,结果表明当坝基处于弹性状态时,超载试验结果可用于坝体稳定性的定量分析;黄岩松等[10]运用三维非线性有限元软件进行了坝体非线性超载分析,计算结果表明在岩体内部的结构面对坝体稳定性的影响大,对结构面进行加固处理可大大提高坝体稳定性;梁形形[11]在对尾矿坝渗流分析的基础上,总结出尾矿库浸润线的变化规律,并对某尾矿坝浸润线进行预警。
目前针对尾矿库稳定性验算和重力坝超载安全度研究较为多见,而针对尾矿坝超载安全度的试验研究不多。笔者通过尾矿坝超载安全度模型试验,分析超载过程中尾矿坝的变形特征和破坏特征,并分析数值计算结果(强度折减系数)与超载试验结果(试验超载安全系数)的差异。研究结果可为尾矿坝新建、运营、溃坝地质灾害防治提供指导。
1 尾矿坝倾斜抬升超载安全度试验
1.1 试验原理
利用模型箱进行相似模拟试验,采用倾斜抬升法施加超载,在模型箱一端倾斜抬升一定角度过程中,尾矿坝的抬升角度变大,整个坝体的下滑力不断增加,直到尾矿坝失稳破坏,失稳破坏时安全系数K′与初始安全系数K的比值即为超载安全系数KSP。超载安全系数计算如图1所示。

(a)抬升前

(b)抬升后
由图1(a)可知,模型被倾斜抬升前,用抗滑力R与下滑力T计算该尾矿坝的安全系数K:
(1)
式中:W为物体自重,g/cm3;Wx、Wy为W的2个分量,g/cm3;f′为摩擦角,(°);C′为黏聚力,kPa;A为单位宽度接触面积,cm2。
由图1(b)可知,模型抬升一定角度后,用抬升后抗滑力R′与下滑力T′计算尾矿坝的安全系数K′:
(2)

通过K与K′的比值确定超载安全系数KSP:
(3)

(4)
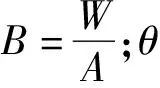
因尾矿库大部分由尾砂组成,且在滑动面处黏聚力极小[12-13],故取黏聚力C′=0,则有:
(5)
1.2 试验设备与材料
相似模拟试验箱物理尺寸为100 cm×40 cm×25 cm,在试验箱前端架设高速工业相机,试验系统如图2所示。试验材料为阜新市同乃铁矿尾矿库原尾矿砂,其干密度为1.92 g/cm3,含水率为13.2%。
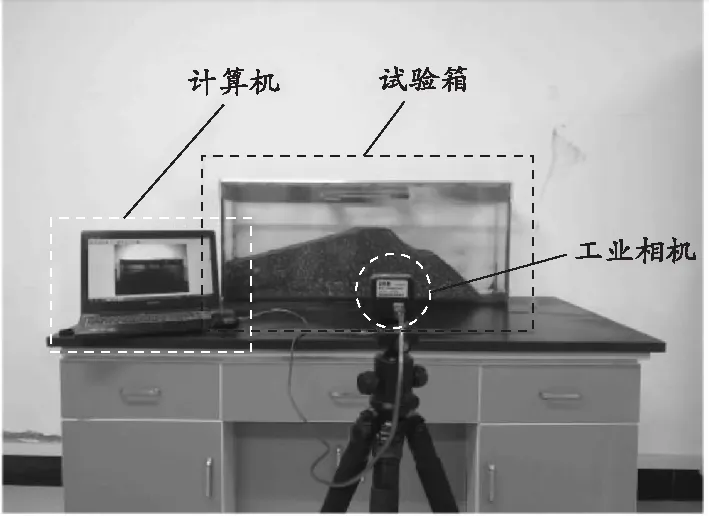
图2 尾矿坝相似模拟试验系统
1.3 试验方案
用数字图像技术分析试验过程尾矿坝变形特征。超载施加时,每次抬升角度为0.5°,抬升过程中记录模型的裂缝发育情况,直到裂纹贯通时停止试验。模型物理尺寸及监测点布置如图3所示。
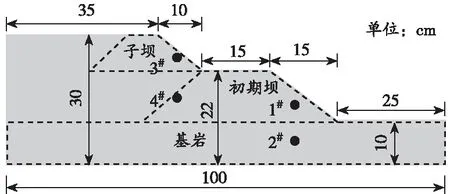
图3 模型物理尺寸及监测点布置图
2 试验结果与讨论
2.1 位移变化特征
用位移曲率突变准则判定尾矿坝稳定性,尾矿坝位移监测结果如表1所示,监测点位移变化曲线及其曲率变化曲线如图4所示。

表1 尾矿坝位移监测结果

图4 监测点位移变化曲线及其曲率变化曲线
由表1与图4可知,整个试验过程初期尾矿坝1#监测点的位移最大,然后依次是3#、4#、2#监测点;试验结束时,1#监测点的位移为7.56 mm,2#监测点的位移为1.21 mm,3#监测点的位移为2.30 mm,4#监测点的位移为1.73 mm。
4个监测点中,2#、3#、4#监测点的位移在初期骤然增加,随后位移缓慢增加,位移监测曲线平滑;1#监测点的位移在初期增长较快,在经历一个缓慢增加过程后,在尾矿坝抬升角度8.5°至9.0°过程中位移由2.64 mm急剧增加至3.08 mm,此时位移发生突变,边坡失稳破坏,对应的安全系数为1.38;在尾矿坝抬升角度大于9.0°后,1#监测点的位移骤增明显。根据位移曲线曲率变化,1#监测点的曲率发生突变,突变从尾矿坝抬升角度8.5°开始,尾矿坝抬升角度9.0°时明显突变,可判定本试验计算的超载安全系数在1.35~1.38内。
2.2 破坏特征
超载安全系数由抬升角度换算而来,滑动面演化如图5所示。

图5 滑动面演化图
由图5可知,当超载安全系数为1.17~1.19时,尾矿坝初期坝坝脚处发生破坏;当超载安全系数为1.24~1.26时,尾矿坝初期坝坝脚处的滑动面拓展,同时初期坝坝顶处和子坝坝脚处均出现破坏区;当超载安全系数为1.26~1.28时,初期坝坡脚的裂缝持续拓展,子坝处的裂缝拓展缓慢;当超载安全系数为1.31~1.33时,初期坝坡顶的破坏裂缝增加至2条,坡脚裂缝拓展至初期坝坝高2/3位置,初期坝处裂缝即将贯通。
当超载安全系数为1.35~1.38时,初期坝坝脚处拓展的裂缝与初期坝坝顶第1条裂缝形成贯通裂缝,初期坝坝顶第2条裂缝在小范围拓展,子坝裂缝急剧拓展。再增加抬升角度,初期坝裂缝完全贯通,初期坝坝顶后端出现第3条裂缝,且初期坝坝顶第2条裂缝与已贯通的裂缝贯通,持续极短时间后初期坝沿着裂缝滑移,滑移体堆积在初期坝坝脚位置。分析得出:发生裂缝贯通的超载安全系数区间为1.35~1.38,坝体发生破坏的超载安全系数区间为1.38~1.40。
3 尾矿坝倾斜抬升超载安全度数值模拟
3.1 数值模拟方案
根据试验尾矿坝的断面建立数值计算模型,模型尺寸如图3所示,试验尾矿坝断面模型如图6 所示。

图6 试验尾矿坝断面数值模拟模型图
试验尾矿坝断面模型一共划分为8 487个单元,17 472个节点;计算模型采用莫尔-库仑理想弹塑性模型,计算参数根据试验尾矿坝尾砂室内试验测得,尾矿的密度为1.92 g/cm3,体积模量为 6.25 MPa,切变模量为2.88 MPa,黏聚力为15 kPa,摩擦角为30°。计算过程中对超载安全系数进行实时监测,计算折减系数从1.0开始,单次计算完成,对折减系数累加0.1后重新计算,直到边坡完全破坏终止计算。
3.2 裂缝拓展判据
采用极限应变判据判定尾矿坝的破坏状态,理想弹塑性应力—应变曲线如图7所示。

图7 理想弹塑性应力—应变曲线
由图7可知,极限应变破坏准则表述为:在岩土材料稳定性分析时,当岩土材料进入塑性状态并达到极限应变时,岩土材料开始发生局部点破坏;当岩土材料局部破坏点连通已形成贯通的极限应变破坏区时,岩土材料发生整体破坏。该理论已经在混凝土、土质边坡、岩质边坡及隧道工程等领域得到验证[14-15]。
文献[14]探讨了岩土材料极限应变获取方法,岩土材料塑性破坏极限应变为:
(6)

而在塑性状态下ε1、ε3数值难以直接求解,可以引入参数χ1、χ3:
(7)
式中:ε1y为第一弹性极限主应变;ε3y为第三弹性极限主应变。
ε1y、ε3y根据莫尔-库仑准则求出:
(8)
式中:E为弹性模量,MPa;ν为泊松比;σ1为第一主应力,kPa;σ3为第三主应力,kPa。
χ1、χ3由数值模拟分析求得,弹塑性极限应变可表述为:
(9)
3.3 数值模拟计算结果及分析
3.3.1 稳定性计算结果
以极限应变判据作为破坏标准,对尾矿坝的破坏过程和安全系数进行分析。不同强度折减系数条件下,尾矿坝坝体破坏特征如图8所示。
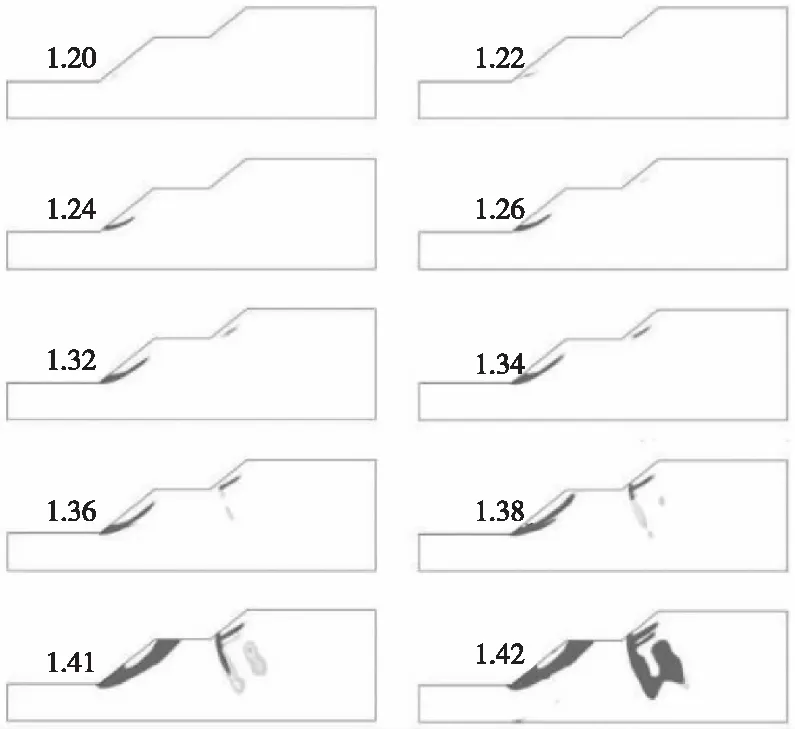
图8 尾矿坝坝体破坏特征
由图8可知,当强度折减系数为1.20时,尾矿坝在初期坝坡脚处开始发生点破坏,尾矿库发生破坏的起始位置位于初期坝坝脚;增大折减系数,点破坏范围扩大,并成为光滑的曲线;当折减系数增大至1.26时,初期坝破坏面拓展至初期坝坝高的1/2处,在子坝坝高1/2位置处出现点破坏;再增大折减系数,初期坝破坏面向顶部拓展,而子坝破坏面由点破坏变为线破坏,拓展方向为子坝中部向坝脚;当折减系数增大到1.36时,在初期坝1/3位置处的破裂面出现分支,初期坝破裂面呈非圆弧状;当折减系数为1.38时,初期坝破坏面贯通,边坡失稳;继续增大折减系数,初期坝滑动面拓展为圆弧型,子坝出现指向坝基的破坏面。由强度折减系数为1.38、1.41、1.42的破坏特征分析可知,在初期坝局部失稳后还可能出现子坝或者坝身局部破坏。
3.3.2 数值计算与试验结果的对比
对比分析数值模拟与试验结果之间的差异,对比结果如图9所示。

图9 数值模拟与试验结果对比
由图9可知,数值模拟结果中当强度折减系数为1.20时在初期坝坡脚位置出现点破坏;当试验安全系数为1.17~1.19时,出现初期坝坝脚处的点破坏;当试验安全系数为1.24~1.26时,初期坝坝脚、初期坝坝顶和子坝都出现点破坏,而数值模拟结果并未在初期坝坝顶出现点破坏;当试验安全系数为1.35~1.38时,裂缝贯通且在初期坝坝顶出现新裂缝。在数值模拟中,当强度折减系数为1.38时出现贯通裂缝,值得注意的是,虽然初期坝坝顶处未出现第2条裂缝,但在子坝坝脚处出现1条指向坝基深处的张拉裂缝,张拉裂缝出现的位置与试验结果有差别。数值模拟强度折减系数为1.38时破坏区贯通;在试验安全系数为1.38~1.41时坝体滑移,即试验与模拟求得的安全系数吻合。总体而言,试验求得的安全系数和尾矿坝破坏形态两个方面都与数值模拟强度折减计算结果吻合。
4 结论
1)在尾矿库相似模拟试验破坏过程中,初期坝的位移大于子坝的位移,坝基的位移最小;初期坝试验最大位移为7.56 mm,子坝最大位移为2.30 mm,基岩的最大位移为1.73 mm。
2)尾矿坝破坏失稳是由初期坝坝脚处的点破坏发展为整体破坏失稳的演变过程,初期坝坝顶位移及曲率在尾矿坝抬升角度为8.5°至9.0°之间发生突变,裂缝贯通判据与位移曲率突变判据的判定结果一致,试验尾矿坝的超载安全系数为1.35~1.38。
3)通过数值模拟强度折减计算结果与相似模拟试验结果对比分析可知:试验求得的安全系数和尾矿坝破坏形态两个方面都与数值模拟强度折减计算结果基本吻合,说明倾斜抬升超载试验方法适用于尾矿库稳定性的研究。

