岩层钻孔过程中切削模型及影响因素分析
邱东卫,赵志刚,张 伟,郑雅华
(1.山东科技大学 矿业与安全工程学院,山东 青岛 266590;2.山东唐口煤业有限公司,山东 济宁 272000)
在煤矿生产期间需要对岩层进行大量的钻孔施工,锚杆(索)钻孔、瓦斯抽放钻孔、卸压钻孔是常见的钻孔类型,钻孔钻进过程可分为钻头推进压入岩体和转动切削岩体2个基本动作,岩层中钻进过程为边压入边切削的循环进程[1]。钻头转动切削岩体的切削力是岩层钻孔研究的核心内容之一。
关于切削破岩的机理及受力分析,国内外学者进行了大量的研究。徐小荷等[1]提出计算切削力的最大剪应力模型,认为切削时破碎面遵守莫尔-库仑强度理论;Evans[2]通过观察楔形截齿切入岩体中的破坏形态,提出一种按最大拉应力计算切削力的方法;Merchant等[3]针对弹塑性材料切削,提出一种半经验模型,假设剪切破裂面是沿齿尖到岩石表面的一条直线,实验表明该模型适用于煤炭和湿白垩石的切削;胡忠举等[4]实验研究了进给量、刀具前角、切削深度和切削速度对切削力的影响,推导出单位切削宽度的切削力经验公式;马清明等[5]通过改变切削面、切削齿倾角和岩石种类对PDC切削齿切削岩石开展实验研究,根据实验结果建立了切削齿的受力模型;欧阳义平等[6]通过分析现有切削力公式和数据,提出切削力与切削厚度、岩石性质关系的计算公式,并进行了实验验证;祝效华等[7-14]采用数值模拟方法对切削过程中不同压力情况下岩石的破碎形式进行了研究。
目前,尽管对于岩层钻孔破岩受力方面的研究较多,但一方面受钻孔环境等因素制约,获取钻孔内部实测数据较为困难,同时对于钻孔过程的破岩机理和理论模型分析较少,还需要进一步研究并完善。因此,搞清楚转动切削过程中钻头—岩体相互作用关系和切削力特征,分析力学参数等因素对切削力的影响规律,是获取岩体力学性质,提高钻进效率、减少能耗,优化钻头、钻杆、钻机设计的前提和基础。
1 钻孔理论和力学模型
1.1 切削刃破岩机理
钻头在钻进切削岩体时的运动轨迹是螺旋线,由于转速大,螺旋角很小,可以将钻头切削刃的切削运动视为一个直线运动和一个平面转动,即直线压入岩体和平面转动切削破坏岩体,如图1所示。将钻孔钻头进行简化,单独研究切削刃平面转动破坏岩体的切削力。

(a)简化钻头

(b)螺旋钻进

(c)直线压入

(d)平面转动
在岩层中钻孔,在轴向推进力作用下,切削刃压入岩体,钻机的电动机驱动钻头转动,切削刃侧面压缩岩体,给岩体施加压缩荷载,随切削刃转动角位移增加,切削刃作用在岩体上的荷载越来越大,当荷载达到最大值时岩体被破坏,此时钻头切削刃与岩体间的相互作用力即为切削力峰值。岩体破坏被抛出,切削刃与岩体脱离接触,切削力突降至0附近。切削力从0上升至峰值点、然后突降为0就是一次切削过程,切削抛出具有一定大小规格的岩体。该切削过程不断重复,直到完成360°范围内全部岩体切削破坏掉,在这期间切削力呈现出从0增加到峰值然后突降到0的周期性波动规律。实验测定砂岩切削力与切削长度之间的波动变化关系[1],如图2所示。
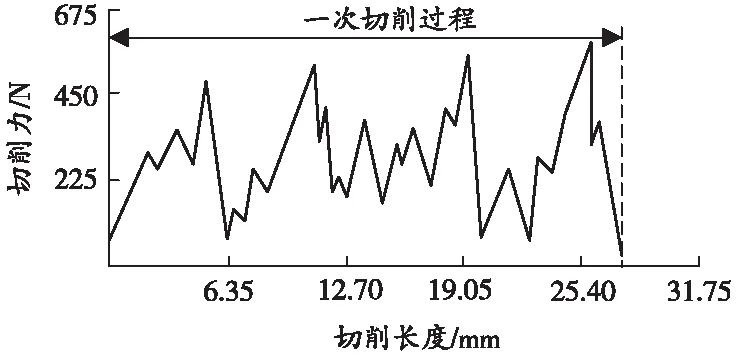
图2 切削力随切削长度变化关系
由图2可知,在切削力从0增加到峰值前,往往还有2~3次小幅度的切削力下降过程,对应的是切落小块岩体。因此一次完整切削过程为:切削刃在电动机驱动下转动,钻头切削刃接触并压入岩体中,切削力开始上升,直至小块岩体被破坏抛出,切削力下降,2~3次小块岩体被破坏抛出后,切削力达到峰值,大块岩体被破坏抛出,钻头切削刃与岩体脱离,切削力突降到0附近,一次切削过程完成。钻头钻进破岩的过程即为不断循环压入和转动切削岩体2个动作,直至钻孔完成。
1.2 切削刃切削岩体静力学模型
为分析岩层钻孔过程切削力的变化规律,作以下假设:
1)切削破岩为平面应力状态。压入深度相比于钻头宽度小很多,认为岩体受力为平面应力状态。
2)作用在切削刃上的力是集中力。有研究测定了切削煤岩体时前刃面上的压力分布,发现最大压力不是发生在切削刃上,而是距离切削刃前方一个很小的距离,离开切削刃略远,压力迅速减小[1]。根据这一事实,可以用作用在切削刃上的集中力代替实际作用的分布力。
3)破裂面为平面,载荷均匀分布。
4)忽略切削刃底部与岩体摩擦力。
5)岩体破坏条件符合莫尔-库仑强度理论。
根据以上假设条件,得到切削刃转动切削岩体的静力学计算图,如图3所示。切削刃压入岩体中深度为h,切削刃角度为2θ,岩体沿角度为α的破裂面发生剪切破坏,破裂面长度为L。

图3 钻头切削岩体静力学分析图
由图3可得,钻头侧面受到水平切削力F作用,F1为岩体对切削刃的作用力,与F互相平衡。F′为切削刃对岩体的作用力。破坏面右侧岩体对左侧岩体的作用力为F2。将F′分解为切削刃面法向力R′和切向力S′,则:
R′=F′cosθ,S′=F′sinθ
(1)
岩体受力分解示意图如图4所示,将F2分解为R2和S2,这两个力分别与R′和S′互相平衡,大小相等。将R2分解为破裂面法向力NR和切向力TR:
(2)
将S′分解为破裂面法向力NS和切向力TS:
(3)
则作用在破裂面上总的法向力N和切向力T为:
N=NR+NS=R′sin(θ+α)+S′cos(θ+α),
T=TR-TS=R′cos(θ+α)-S′sin(θ+α)
(4)
岩体破裂面上作用的正应力和剪应力分别为:
(5)
式中b为切削刃侧面宽度。
岩体沿破裂面剪切破坏,破坏条件符合莫尔-库仑强度理论,则有:
τ-σtanφ=C=
(6)
式中:C为岩石的黏聚力;φ为岩石内摩擦角。
由式(6)可知,τ-σtanφ是破裂面倾角α的函数,式(6)对α求导并令其为0,可以获得τ-σtanφ的极值。
式(6)对α求导并整理为:
(τ-σtanφ)′=
(7)
将式(1)代入式(7)并整理可得:
(8)

(9)
将式(9)代入式(6)可得:
τ-σtanφ=C=
(10)
整理后得到切削力峰值为:
F=F′=
(11)
2 切削力的影响因素分析
2.1 切削力和切削深度关系
式(11)表明,切削力峰值主要有3个影响因素,分别是:切削深度(或压入深度)h、切削刃角度θ、岩体的力学性质(黏聚力C和内摩擦角φ)。
根据切削力计算公式,切削刃侧面宽度b取 2×10-2m,黏聚力C取5、7、9 MPa,内摩擦角φ取40°,切削刃角度取30°。计算得:切削深度与切削力呈线性关系,在其他参数不变的情况下,切削深度越大则切削力越大,如图5所示。
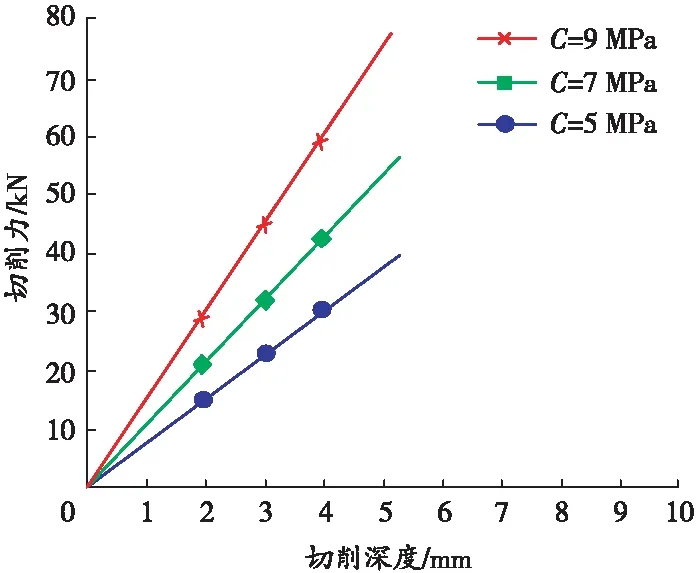
图5 切削深度对切削力影响规律
2.2 切削力和切削刃角度关系
为分析切削刃角度对切削力的影响,对切削力计算公式中切削深度h取2×10-3m,切削刃侧面宽度b取2×10-2m,黏聚力C取5 MPa,内摩擦角φ取40°。计算得:当θ<25°时,切削力随着切削刃角度的增大而增大;当θ=25°时,由公式(11)可得,当 sin(2θ+φ)趋近于0时,破裂角α趋近于0°,破裂面无限长,切削力无限大,即存在最费力的切削刃角度;当25°<θ<90°时,切削力随着切削刃角度的增大而减小。因此在内摩擦角取值为40°条件下,只需分析θ<25°、25°<θ<90°时切削力与切削刃角度的关系,如图6 所示。
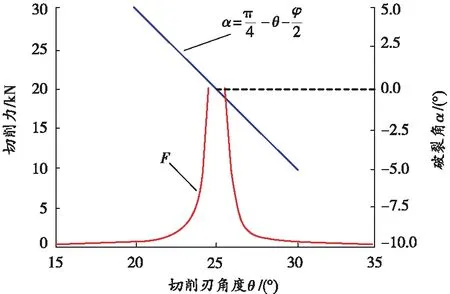
图6 切削刃角度对切削力的影响规律
2.3 切削力和岩体力学性质关系
在同一岩层钻孔时,式(11)中岩石的内摩擦角可认为不变。
为分析岩层的黏聚力对切削力的影响规律,对切削力计算公式中切削深度h取2×10-3、3×10-3、4×10-3m,切削刃侧面宽度b取2×10-2m,内摩擦角φ取40°,切削刃角度取30°。计算得:黏聚力与切削力呈线性关系,在其他参数不变的情况下,黏聚力越大则切削力越大,如图7所示。

图7 黏聚力对切削力的影响规律
3 转动切削模型验证
PRADEEP L等[14]研究发现,对于岩层中旋转钻孔诸多影响因素,按照主次关系的排序是:轴压、转矩、回转速度和岩石硬度,轴压对应的就是切削深度,即每单周旋转的压入深度h。邓嵘等[15]进行了单牙轮钻头切削破岩试验,研究齿形、岩石性质、切削深度、切槽间距和切槽交叉角度对破岩的影响,实验选用了2种典型砂岩样本,一种砂岩代表软砂岩,另一种砂岩代表硬砂岩,取软砂岩的黏聚力 5 MPa、内摩擦角30°,硬砂岩的黏聚力10 MPa、内摩擦角40°,按照公式(11)切削刃角度取30°,利用该文献的实验数据对本文切削力公式进行验证,绘制切削力—切削深度曲线,如图8所示。
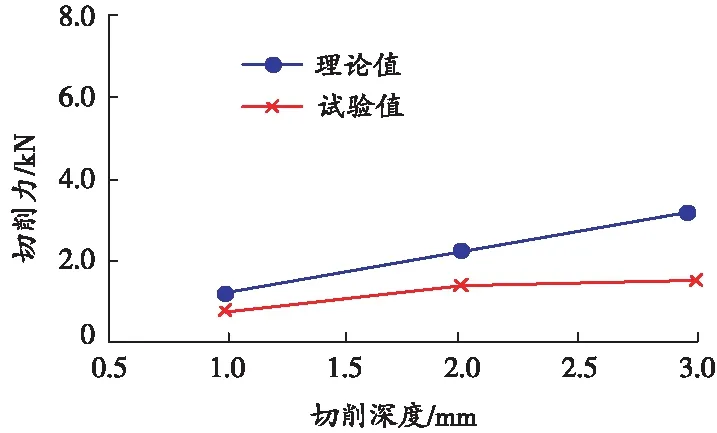
(a)软砂岩
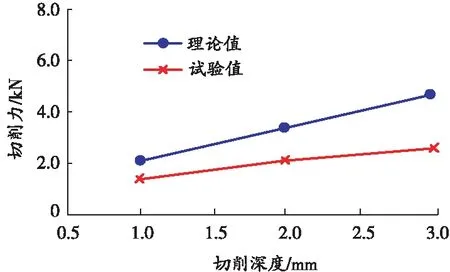
(b)硬砂岩
由图8可以看出,切削力随切削深度线性增加,变化规律与本文的理论分析计算结果规律一致。
4 结论
将岩层钻孔分解为轴向压入岩体和旋转切削岩体2个环节,通过对切削刃旋转切削岩体进行静力学分析,建立了转动切削力学模型,得到如下结论:
1)切削深度(或切削厚度)对切削力影响较大,钻头形状不变,在同一岩层中切削深度越大,所需的切削力越大;反之,所需的切削力越小。切削力与切削深度之间呈线性递增关系。
2)在切削深度一定的情况下,破岩所需最大切削力与切削刃角度有关,同种岩层体中,切削刃角度较小时,对切削力影响较小,当增大到一定角度时,存在最费力的切削刃角度。
3)钻头形状不变,相同的切削深度,岩石越硬越难切削,切削力与煤岩体黏聚力之间呈线性递增关系。

