一种活塞式压力计的数值研究方法
张忠立 秦亭亭 王灿 洪扁/.上海市计量测试技术研究院;2.复旦大学
0 引言
活塞式压力计是一种利用流体静力平衡原理进行压力量值传递的计量标准器[1]。活塞式压力计的测量原理基于公式p=F/A,因此活塞式压力计在压力量值传递中,最关键的因素是活塞有效面积[2-5]。目前国内依据JJG 59-2007《活塞式压力计》检定规程[6],通过直接平衡法或起始平衡法对活塞有效面积进行量值传递,其影响因素主要有活塞杆的转速、流体的黏度、活塞杆与活塞筒的弹性模量等。截止目前的文献显示,国内的文献大多为活塞式压力计的不确定度分析以及部分试验研究,并未深入开展对活塞式压力计的理论研究,其难度主要在于传统实验无法保证上述影响因素的单一控制。因此,本文提出一种针对活塞式压力计的数值研究方法,利用ANSYS软件进行流固耦合分析,以0~250 MPa压力范围的简单型活塞压力计为例,研究其活塞间隙中的流体压力分布以及不同平衡压力下的活塞有效面积,可为将来的活塞式压力计各影响因素的理论分析研究提供借鉴与思路。
1 模型的建立与设置
采用 ANSYS Workbench 17.0 进行瞬态的仿真,分别利用Transient Structural模块和Fluent模块进行固体域和流体域分析,并引入System Coupling模块进行双向耦合分析。本次活塞式压力计研究模型中,活塞杆旋转并受流体压力而产生形变,同时活塞杆的形变又导致流场的改变,因此采用双向流固耦合分析更加合理。
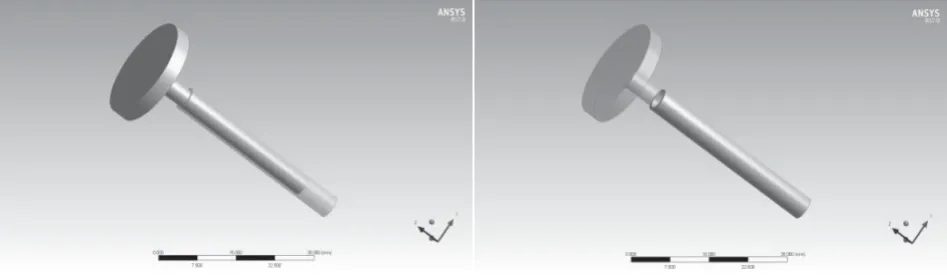
图1 活塞式压力计模型
模型总共分为两个部分:其中活塞杆(固体域)由一个直径为20 mm、厚度为3 mm的顶部圆盘连接一个直径为3.55 mm、高度为37.5 mm的圆柱组成;活塞工作介质(流体域)位于活塞杆顶部圆盘下方7.5 mm处,其直径为4.55 mm,高度为37 mm;活塞杆与活塞筒之间的间隙为0.5 mm;活塞工作介质与活塞杆之间的接触面即为流固耦合面。
1.1 固体域设置
活塞杆的材料设置为碳化钨(Tungsten Carbide),其材料参数如表1所示。

表1 碳化钨材料参数
活塞杆采用ANSYS自带的Automatic Method方法进行网格划分,其网格图及网格质量如图2所示。
本次研究模型中,时间步设定为0.003 s,总运行时间为0.6 s。整个活塞杆以30 rpm的角速度旋转,旋转 0.6 s恰好转过108°。

图2 固体域网格划分及网格质量图
1.2 流体域设置
网格划分采用的是Tetrahedrons方法,其网格划分及网格质量如图3所示。流体域选择瞬态分析,同时开启重力设置,模型采用 Realizable k-epsilon(2 eqn)。流体域底部的入口压力根据0~250 MPa进行选择设定,其出口压力设置为0 Pa。选择求解方法为PISO,PISO算法是SIMPLE算法的一种改进形式,它对于瞬态问题比SIMPLE算法更有优势。相比较之下,PISO算法在解决瞬态问题时在同一时间步内的迭代次数更少,给出的解也更稳定[7]。

图3 流体域网格划分及网格质量图
1.3 研究方法
简单型活塞式压力计在平衡时,根据活塞的重力GP,砝码载荷F,平衡压力p以及有效面积A,理论上应该满足:

为了在ANSYS中量化活塞的平衡状态,对活塞施加额外的约束,并通过观察这一约束反力来判断活塞是否平衡,即此时,活塞式压力计模型中,活塞杆的受力变为:

式中:FRD——约束反力
由此可得活塞的有效面积计算公式:
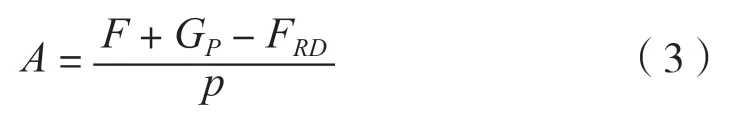
本文选取 50 MPa、100 MPa、150 MPa、200 MPa、250 MPa这5个平衡工作压力点进行流固耦合分析,并根据相应平衡压力和活塞杆几何模型的初始面积A0,计算得到活塞平衡时的初始砝码载荷F,即:

在完成流固耦合的收敛计算后,将稳定后的约束反力代入式(3)计算得到相应的活塞有效面积。
2 结果分析与讨论
以平衡工作压力50 MPa的情形为例,根据施加的约束,查看其约束反力。整个计算周期的约束反力变化曲线以及其0.5~0.6 s期间的放大图如图4所示。
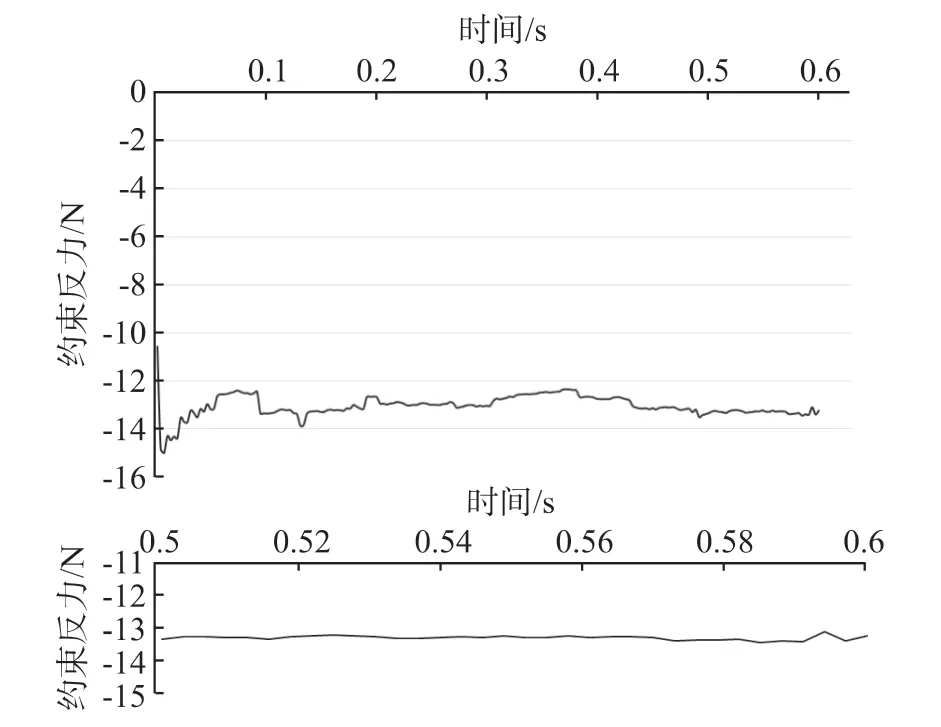
图4 约束反力变化曲线以及0.5~0.6 s放大图
由图可见,活塞系统运行0.5 s之后,也就是活塞转过90°之后,约束反力基本在-13 N附近变化,这说明0.6 s的运行时间已能够得到较为稳定的解,也进一步验证了计算时间选取的合理性。对0.5 s到0.6 s之间的数据进一步处理,如表2所示。

表2 50 MPa 时运行 0.5 s 至 0.6 s 之间的数据特征
代入式(3)计算,就可以得到50 MPa时活塞的有效面积:

2.1 活塞间隙的流体域压力分析
以平衡工作压力250 MPa的情况为例,通过添加一个平行于Z轴的截面,可以观察到流体域压力的分布与变化如图5所示。

图5 250 MPa平衡工作压力下的流体压力分布
从图5可见,活塞杆底部的流体压力约为250 MPa,进入活塞间隙后,压强减小,直至压力出口基本接近于0 Pa,符合本文所设定的边界条件。为了进一步分析压力在流体间隙径向的变化,沿着Y方向(X=0平面,Z坐标为-22.5 mm),选取同一直线上的5个流体压力监测点,间隔为0.1 mm。
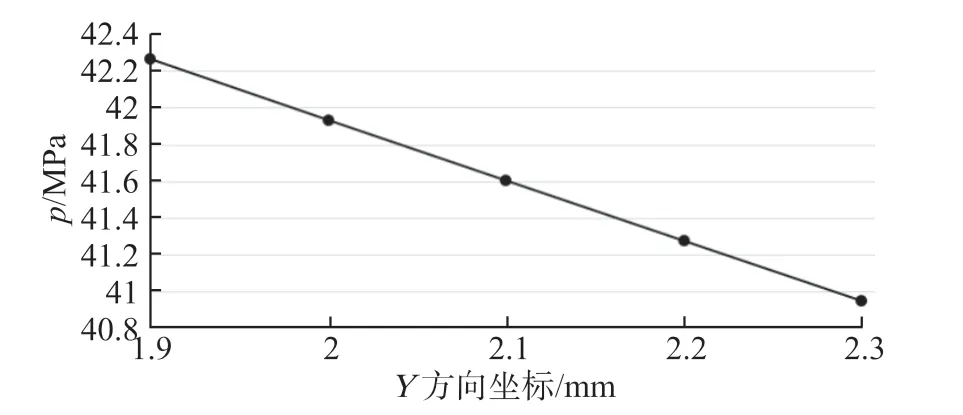
图6 平衡工作压力250 MPa下流体间隙径向压力变化曲线
由图6可见,活塞间隙中流体压力基本上随着远离活塞壁面而近似线性减小,进一步研究不同平衡工作压力下的变化情况,仍选取这5个流体压力监测点,其结果统计如表3所示。

表3 不同平衡工作压力下的各监测点压力变化(单位:MPa)
根据表3数据,计算不同平衡工作压力下的压力变化梯度,即下降速率,结果如图7所示。
由图7所示,随着平衡工作压力的增大,活塞间隙流体压力的径向下降速度的幅度基本上呈现近似线性增大。同理,在活塞间隙的轴向(Z方向)设置6个间隔为5.8 mm压力监测点,分布于X=0平面且Y=2.15的轴线(活塞间隙的中心轴线),将压力数据作为图8。

图7 流体间隙径向压力变化梯度曲线

图8 流体间隙径向压力变化梯度曲线
由图8可见,曲线的第一个监测点(Z=-37 mm)的压力值远远低于平衡工作压力,约为入口平衡工作压力的30%左右。可见,活塞底部间隙的短短0.5 mm长度,是压力快速下降的阶段。从(Z=-30 mm)至流体出口的区间,活塞间隙中流体压力基本呈现线性下降的趋势。
2.2 活塞有效面积的分析
活塞有效面积为活塞式压力计压力量值复现中最为主要的量值,根据相应改变活塞平衡工作压力和其他相应参数设置,求得各个平衡工作压力下的约束反力,如表4所示。
将表4中数据代入式(3)中,计算各个平衡工作压力下的活塞有效面积,结果如图9所示。可以看出,随着平衡工作压力的不断增大,有效面积呈现逐渐减小的趋势,且其减小的速度随着平衡压力的增大而减缓。
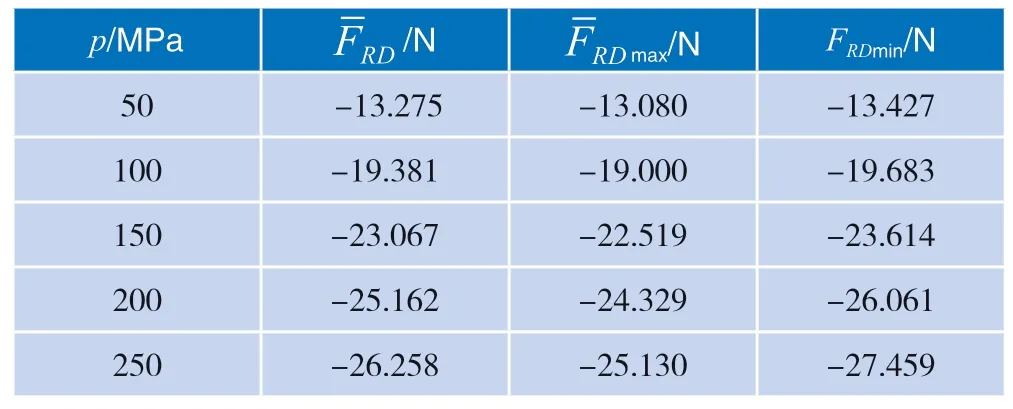
表4 各个平衡工作压力下的约束反力

图9 不同平衡工作压力下活塞有效面积变化曲线
3 结语
基于ANSYS流固耦合仿真技术,提出了一种活塞式压力计的数值研究方法,并以0~250 MPa压力测量范围的简单型活塞式压力计为例,验证了该方法的可行性,并计算和分析了不同平衡工作压力下活塞间隙流体压力分布与活塞有效面积的变化规律,结论如下:1)活塞间隙中流体压力基本上随着远离活塞壁面而近似线性减小,且下降速度与平衡工作压力呈现近似线性关系;2)活塞间隙流体从底部入口至顶部出口的过程中,流体压力先是通过0.5 mm长度,快速下降至平衡工作压力的30%左右,再线性下降至出口为零;3)随着平衡工作压力的不断增大,有效面积呈现逐渐减小的趋势,且其减小的速度随着平衡压力的增大而减缓。这种活塞式压力计数值研究方法,能有效搭建简单型活塞式压力计的三维理论研究模型,为活塞式压力计的理论研究提供新的思路。

