基于低相干K-SVD和SVM的齿轮故障诊断方法研究

魏永合，李宗霖，唐英瀚，李宏林，马步芳

(1.沈阳理工大学 机械工程学院，沈阳 110159；2.加州大学河滨分校 马兰和罗斯玛丽·伯恩斯工程学院，美国 加州)

机械设备在使用过程中，如果出现故障，很容易造成重大事故和损失。齿轮作为广泛使用在机械设备中的零件，其故障也是机械设备普遍存在的问题[1]。如能及时判断出故障的类型或程度，则可挽回较多不必要的损失。

机械设备故障诊断技术首先通过实验设备采集机械设备的信号；再通过特征提取的方式，提取出反应故障特征的信号；最后由模式识别算法依据故障特征信号，判别出设备的故障类型、程度等[2]。其中，特征提取和模式识别是该技术的关键。

对于轴承前期故障，难以明显的在其时域、频域中观察到故障信息。由此，余发军等[3]通过改进型的K-SVD(K-Means Singular Value Decomposition)[4]和在稀疏分解过程中找出逼近信号以判断出轴承故障类别。张兆珩等[5]利用移不变字典学习特征成分的字典，有效提取了故障信息，且分辨出了其故障类型。这两种方法都解决了对轴承微弱信号的特征提取，并判别出了其故障类型。由此，可以借鉴其采用的算法，将齿轮箱中的故障信号提取出来。

模式识别是判别故障类型或故障程度的机制，对于小样本问题，在现有模式识别方法中，支持向量机(Support Vector Machine，SVM)具有更好的识别效果[6]。潘礼正等[7]通过小波包和独立成分分析的特征提取方法，采用SVM算法识别齿轮的四种故障类型，具有良好的识别效果。韩霞等[8]采用遗传算法，优化了SVM分类模型，并通过实验表明优化后的SVM模型具有较高的分类正确率。

针对传统K-SVD存在的问题，即字典原子间具有较高相干性导致构建出的字典不足以准确匹配信号特征，本文提出了低相干K-SVD结合SVM的齿轮故障诊断模型，用以提高齿轮信号的重构性能以及齿轮故障状态识别的准确率。

1 低相干K-SVD算法

K-SVD算法试图将样本集分解成字典D与稀疏编码α相乘的形式。K-SVD算法结合了K-Means与奇异值分解(Singular Value Decomposition，SVD)的思想，分别固定字典D或稀疏编码α，采用SVD不断更新字典的每一列，并用正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法[9]对α进行更新，直至达成终止条件为止。

K-SVD的目标函数可构造为

(1)

式中：D表示N行K列的字典；α表示稀疏编码；αi表示第i行稀疏编码；ε表示阈值；F表示F-范数；0表示0-范数；X表示样本矩阵。

K-SVD对字典D的更新见式(2)。

(2)

当固定稀疏编码α后，从字典D中挑出某一列，构成该列的残差矩阵E，再由SVD对其进行分解并构造原子。然而，如果得到的字典原子间有着过高的相干性，则会导致重构信号不能很好的显示出原始信号的内部结构特征。低相干K-SVD算法就是在传统K-SVD算法的目标函数上加入约束项，从而使得字典具有稀疏性以及低相干性[10]。

字典各原子间的相干性指标采用互相关来定义，如式(3)所示。

(3)

需要指出，对于过完备字典D∈RN×M，其相干性满足式(4)。

(4)

式中N和M表示过完备字典的行和列。

Tropp等[11]指出，仅在字典满足等角紧框架且M≤N(N+1)/2时，式(4)的等号成立[12]。

由此，低相干K-SVD的目标函数可构造为

(5)

式中：I表示单位矩阵；λ0为拉格朗日乘子。

即：在满足α足够稀疏的同时，也要满足字典间相干性最低，其更新过程与原始的K-SVD同理，区别在于对残差矩阵进行SVD分解后，采用能满足式(5)的左奇异向量与其对应的奇异值更新原子。

2 SVM算法基本原理

20世纪60年代，Vapnik等[13]发现了SVM，其试图在样本集中依据支持向量确定一个决策平面，并利用核函数的特性，将在高维空间中难以计算的内积简单有效地计算出来，避免维数灾难对SVM造成的影响。如此，可将非线性问题转换成线性问题并解决。同时，SVM采用小样本即可得出全局最优解的机器学习模型，其基本原理如下。

给定{(x1，y1)，(x2，y2)，…，(xn，yn)}样本集，xi∈Rn为特征向量，R表示实数域；n表示总样本的个数。为找到合适的决策平面，依据其支持向量，可构造如下目标函数

(6)

式中：w表示权重；wT表示权重的转置；xi表示第i个样本；ξi表示阈值；b表示截距；yi为第i个决策平面；n表示样本个数。

式(6)表示，在样本集中希望找到最大间隔的分类超平面。为能更有效地求解，可将式(6)转变为其对偶形式，即选取适当的核函数K(xi·xj)以及惩罚因子C，其优化问题变为

(7)

式中λ1i为拉格朗日乘子向量，λ1i和λ1j分别对应其中不同的值。由此，可以通过式(7)的解，得出式(6)的解。通过式(7)可得出其决策函数，如式(8)所示。

(8)

在SVM的数学模型中可以发现，SVM模型的泛化性能主要受核函数和惩罚因子的影响。为了能够自适应地找到适合样本数据的参数，选用遗传算法优化这两个参数，以求其自适应地找到最优解。

3 低相干K-SVD和SVM的齿轮故障诊断模型

3.1 EEMD和低相干K-SVD模型的构建

原始的K-SVD算法在计算得出的字典中，其各原子之间具有很强的干扰性，为解决这个问题，可采用低相干K-SVD算法，降低各个原子之间的相干性[15]。为进一步提高信噪比，再联合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)算法，其具体实现步骤如下。

(1)将信号EEMD分解，依据峭度值选取本征模态分量(Intrinsic Mode Fuction，IMF)作为样本，并将其矩阵化。

(2)初始化字典D以及样本矩阵都输入到正交匹配追踪算法中，以获得稀疏系数矩阵，再通过低相干的K-SVD得到更新后的字典。

(3)将样本矩阵化后，通过OMP算法得到稀疏系数矩阵。与(2)得到的字典重构，得到稀疏信号矩阵，并将其展开成一维信号。

(4)由其时域、频域特征指标计算构建故障信号特征矩阵，最终得到机械设备的故障信息。

3.2 遗传算法优化支持向量机分类模型

遗传算法优化SVM分类模型，实现步骤如下。

活动二：寻找物质变化的规律。教师引导学生回顾生态系统中的学习，先组织各小组讨论图3并交流。学生得出规律1：物质在食物链的生物间进行循环。学生再通过观察池塘中鱼类饿食物链，推理食物链中有毒物质的传递规律：有毒物质沿食物链富集。

(1)初始化种群数，将SVM中两个必要优化的参数采取二进制编码，种群数设置为20。

(2)以SVM分类的准确率为个体适应度，判断其是否收敛或达到迭代次数，若满足则输出最优解；否则进行下一步。

(3)采取遗传算子对当前一代种群作出处理，本文中交叉概率pc=0.7，变异概率pm=0.05。对新的群体转到(2)，重新计算其适应度。

(4)不断循环(2)和(3)，直到满足终止条件为止。

将得出的参数输入到SVM，最后获得故障诊断的效果。

4 实验验证

本文采用旋转机械故障模拟实验台，模拟齿轮故障，齿轮的特征参数如表1所示。

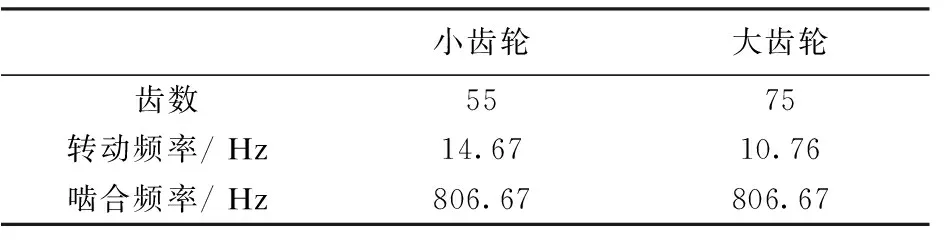
表1 齿轮特征参数

电机转速为880r/min，采样频率为5120Hz。利用加速度传感器分别采集在大齿轮正常、断齿和点蚀情况下的振动信号。图1为三种情况下振动信号波形图。

由图1可知，用加速度传感器采集的信号存在明显的噪声。对采集好的信号分别采用EEMD分解，以峭度为依据提取峭度最大对应的IMF分量。在图1b和图1c中，大齿轮点蚀与断齿信号中带有大量噪音，而经过EEMD与低相干K-SVD结合的算法后得出的信号，相比之下信噪比得到了提高。其经过EEMD分解的IMF分量各状态的峭度值见表2所示。

表2 IMF分量的峭度值

从表2中可以看出，当齿轮出现点蚀时，最大峭度对应第一个IMF分量。断齿情况下对应第二个IMF分量，。

以步长为1，分别选取最大峭度值对应的IMF分量进行矩阵化。通过低相干K-SVD算法，求解出稀疏信号矩阵并将其展开成一维信号，如图2所示。

从图2中可以看出，相比原始信号，其信噪比有了很大的提升。

对重构的一维信号，计算其在时域、频域上的特征，形成特征矩阵。将通过采样得到的样本集分成训练集与测试集。本实验对三种情况下的齿轮分别采集50组数据，其中每类选取30组样本作为训练集，余下构成测试集。采用1，2，3对应三种情况下齿轮状况，为数据添加标签。通过上述方法构造特征矩阵，采用遗传算法优化SVM。设置遗传算法参数如表3所示。

表3 遗传算法参数

遗传算法优化的SVM适应度曲线如图3所示。

图3表示，遗传算法优化SVM得出的最优值所对应的准确率为92.222%，其油画的高斯核函数参数和惩罚因子的值分别为15.0505和19.5324。

将这两个参数用于SVM中，并在训练集中使SVM训练出最大间隔超平面，最后由测试集衡量该分类模型的准确率，如图4所示。

在图4中，可以看出该模型的准确率达到90%(54/60)。

5 结论

提出一种基于低相干K-SVD和SVM算法的齿轮故障诊断模型，改良了原始K-SVD算法中字典间干扰较强的问题；并采用EEMD算法结合低相干K-SVD的方式进一步提高了振动信号的信噪比；为提高SVM模型分类的准确率，采取遗传算法对其优化。实验表明，该方法可有效提高信号的信噪比及准确分辨出信号的故障类型。