一种基于三维编码修正的重叠联盟形成方案

韩 露， 聂艳艳， 程文丽， 臧思雨

(安徽理工大学 经济与管理学院， 安徽 淮南 232001)

0 引 言

团队协作已渐成为在面对并行多任务时的首要选择。个人与个人之间、小组与小组之间、企业与企业之间相互合作已成为新时代的常态。由于每个个体拥有的能力不同，所获的资源不同，在面对并行的、综合的任务时，合理组成有效联盟进行任务求解将在一定程度上实现效率最大化、资源浪费最小化以及任务总收益最大化的完美结合[1]。

随着计算机科学技术的迅速发展，agent理论、多agent系统(Multi-agent systems，MAS)等概念应运而生，基于MAS的联盟研究也受到广泛关注[2]。多agent系统中的重叠联盟形成(overlapping coalition formation，OCF)，在求解复杂并行分布式任务时，各agent之间取长补短、亲密协作，求解任务灵活性强，解决了单个agent因资源不足而无法满足任务需求或勉强完成任务但效率低下的问题。为此，蒋建国等提出了一种基于能力向量发挥率和拍卖的联盟形成策略，在面向任务的领域中可以达到全局优化解，较好地满足了稳定性、时效性、分布等要求[3]；张国富等提出将有效联盟的剩余能力转移给一个动态的虚拟联盟，由虚拟联盟帮助解决其他无效联盟，研究如何把一个无效的二维二进制编码修正为一个合法的编码[4]。

基于上述背景，本文将二维二进制编码扩充至三维整数编码，构建“任务”、“资源”、“agent”于一体的三维空间坐标系，更直观、有效地完成智能资源体的快速分配，并针对联盟形成过程中可能出现的资源冲突与联盟无效问题，提出相应的三维编码修正方案。

1 OCF数学模型

设MAS中的agent个数为n，A={a1,a2,…,an}，需要求解的任务数为m，T={t1,t2,…,tm}。

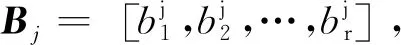
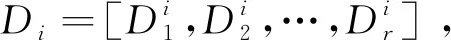
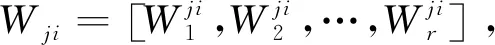
(1)

(4)用V(Ci)表示联盟Ci的值，式(2)[6]：

(2)

其中，φ(ti)为完成任务ti获得的报酬，一般为常数；θ(Ci)为联盟Ci中所有agent成员的总资源成本，即为联盟中各成员实际贡献的资源和；Π(Ci)为任务ti的求解联盟Ci中各agent成员两两之间的通信成本之和，πi1i2为ai1与ai2之间的通信成本。重叠联盟形成问题即为在满足上述约束条件的基础上使V(Ci)值尽可能大。

2 三维整数编码

2.1 符号约定

为了方便描述与理解，将方案中涉及的相关概念符号整理见表1。

表1 修正方案符号说明

2.2 编码修正方案

Step1计算此时每个任务的完成情况，式(3)、式(4)：

(3)

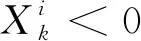
(k∈1,2,…,r;i∈1,2,…,m.)

(4)

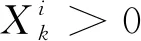
(5)

Step2计算此时每个agent的资源消耗情况，式(6)、式(7)为：

(6)

(k∈1,2,…,r;j∈1,2,…,n).

(7)

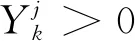
(8)

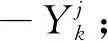
Step3根据step1中计算结果，做出调整以保证所有任务皆可完成，具体步骤如下：

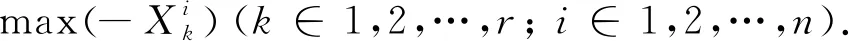
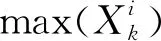
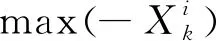
Step6根据最终更新的结果，做出调整以满足所有agent的资源贡献均在其能力范围内，即避免资源冲突，具体步骤如下：

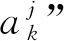
3 实例分析

假设有2个agent，其所拥有的资源向量分别为B1=[2,3],B2=[3,2]，需求解的任务数为2，其对应的资源需求向量分别为D1=[4,3],D2=[1,1]，如图1所示。

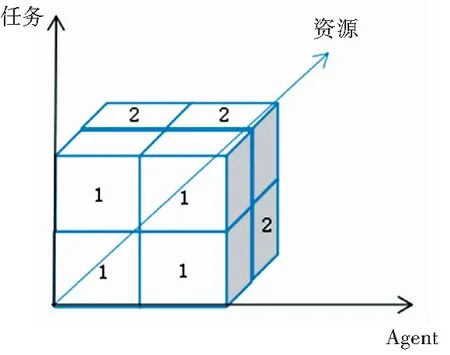
图1 三维空间坐标系示意图

根据能力约束条件产生的初始联盟如下：

编码修正过程：

Step1首先计算此时每个任务对应每种资源的完成情况：

Step2计算此时每个agent的每种资源消耗情况：

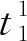
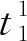
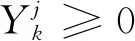
4 结束语

为了更直观、有效的挖掘重叠联盟，本文采用了三维整数编码的表示方式，并提出一种新型的三维编码修正方案。传统的二维二进制编码只能表示各Agent成员是否参与联盟，而不能显示各成员在联盟中贡献的资源量，二维二进制编码和整数混合编码过于复杂和冗余。因此，本文构建了“任务”、“资源”、“agent”于一体的三维空间坐标系，并针对初始化赋予任意值可能产生的联盟无效与资源冲突问题，设计了相应的编码修正策略，以确保任何一个无效编码都能够被修正为一个合法编码。