信号交叉口下游直线式公交站点延误影响分析
汤志江,梁士栋,马晓旦
(上海理工大学 管理学院, 上海 200093)
0 引 言
为了便于两条垂直公交线路上的乘客换乘,城市公交站点通常情况下会被设置在靠近交叉口处,公交站点根据类型可以划分为直线式公交站点和港湾式公交站点两种。根据其布设位置又可以分为交叉口上游公交站点和下游公交站点两种。当路侧布设直线式公交站点时,公交车在站点停靠不仅对其它道路车辆的运行产生影响,同时也间接影响了公交车自身在交叉口处的排队和释放过程。由于延误的传递性,受到延误的车辆数量会随着停站公交的数量和时间的增加而增加,从而在一定程度上干扰了道路尤其是交叉口处车辆的正常运行[1]。
目前,关于公交车延误影响的相关研究主要考虑公交车在站点处停靠对公交车自身、其它社会车辆以及行人造成的延误。如Gibson针对大流量公交站提出公交在站点停靠对社会车辆及行人造成的延误[2];王茜、杨晓光(2003)等通过对公交占用外侧混合车道停靠的定量分析,建立了公交停靠损失、站台位置、公交到达频率与交叉口车辆延误的相互关系,并建立相应的延误影响模型[3];葛宏伟等人基于公交停靠不同的布置形式,采用定性与定量相结合的方法分析了不同布置形式下公交停靠占用时的影响因素及过程,得到公交停靠对路段交通流的影响模型[4];杨孝宽等通过实地调研与分析,基于不同类型公交到达频率和公交影响时间,得到了公交频率与路段通行能力的关系[5];冯伟通过研究路边停车带与路段机动车流速度、行程延误和通行能力等方面的影响关系,定性并定量的分析了路边停车带对路段交通流的影响[6];Gu W等利用迭代法对交叉口上游和下游公交站点处受公交停靠所产生的车辆延误进行分析,并给出两种站点下缩短延误的公交控制手段[7]。
通过对近年来相关研究发现,针对下游公交站点延误问题的分析相对甚少,并且尚未考虑到交叉口处于非饱和状态时受停站公交影响下的车道通行效率降低问题。交叉口下游直线式公交站点对车辆的延误影响,除了与公交车到站时间、停靠时间、站台设置、站台与交叉口位置等相关,还和交叉口信号配时参数相关,这主要体现在由于站台能力不足或者车辆密集到达产生的排队,进而导致交叉口拥堵,上游车辆无法在绿灯时间内有效驶出[8]。因此,本文以交通波理论为基础对下游公交站点处的车辆运行状态进行分析,并结合到站时间和停站时间的不同,将其划分为六种情况进行建模,最后在数值分析部分通过对信号配时参数、公交车在站点处停靠时间以及公交站点与交叉口距离对交叉口下游直线式公交站点的延误进行系统分析。
1 模型构建
1.1 公交停靠下路段通行能力
本文的模型是在Newell交通波理论的基础上,针对交叉口处于非饱和状态下而建立的,为了有效分析公交车在公交站点停靠对道路运行车辆延误的影响,提升所构建模型实际应用的可靠性和可操作性,构建车辆延误模型的条件如下[9]:
(1)交通流处于较为稳定的非饱和状态;
(2)公交车呈离散状态到达且停站时间为一定时间范围内的随机变量。
对于受停站公交影响下的道路通行能力QB,计算方法为公式(1),考虑到由公交停靠产生的临时瓶颈区会出现车辆换道,运行混乱,造成通行效率下降等问题,本文在传统的计算方法的基础上,选取一个折减系数∂,公式(2)。
(1)
(2)
式中,n为车道数;Q为饱和通行能力(辆/s);∂为折减系数。
此外,模型同时考虑到了公交到站时间和公交车停站时间的随机性。利用交通波理论对公交车到站时间求解,得出其概率密度分布函数,结合到站时间和停站时间的不同,绘制在不同状态下的车辆到达累积曲线图,最后利用积分来计算下游公交站点处的车辆延误。
1.2 公交车到站时间分析
由于公交车在一个信号周期内到达下游站点时间是一个均匀分布的过程,部分公交车在到达站点之前会被交叉口处排队等候的小车队列干扰而无法进入站点,同时当交叉口下游车辆产生的消散波尚未到达上游交叉口时,此时公交车也无法进入下游站点。因此,到站时间ta将遵循在一定区间内的均匀分布,其概率密度函数如式(3):
(3)
式中:d为公交站点与上游交叉口之间的距离(m);Lc为交叉口的一个固定信号周期(s);g为绿信比;Q为道路最大通行能力(辆/s);q为自由流状态下道路通行能力(辆/s);QB为受停站公交影响下的道路通行能力(辆/s)。w为小车队伍阻滞时向后产生的后退波波速(m/s)。
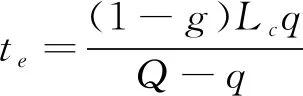
1.3 公交站点车辆运行状态分析
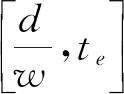
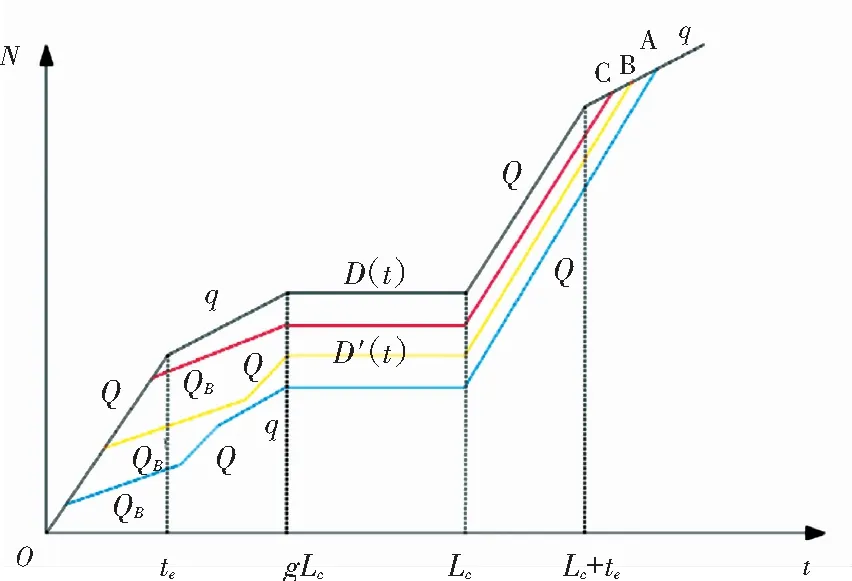
图1 车辆累积曲线图
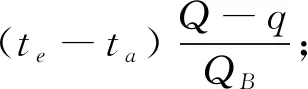
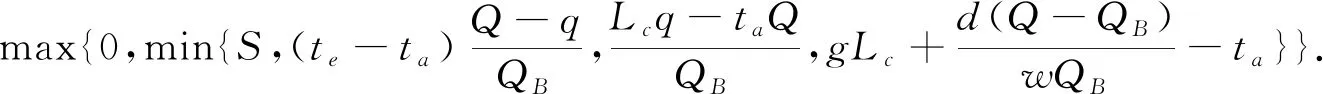
(4)
在TC1之后车流会以饱和交通流Q行驶一段时间,这是因为当公交车开始驶离站点时,受到影响的车辆在以QB到达之后会随公交车一起以饱和交通流Q往下游方向行驶,其通行时间主要取决于TC1结束时的时间和交叉口的信号灯情况,记其为TQ1,计算方法如式(5):
(5)
图1中,上侧的曲线表示无公交车影响下的小车数量累积曲线,用D(t)表示,根据其在各个阶段的通行能力以及端点值可以推算出其在部分区间的表达式为式(6):
(6)
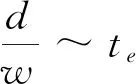
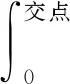
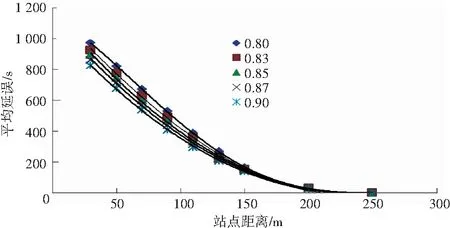
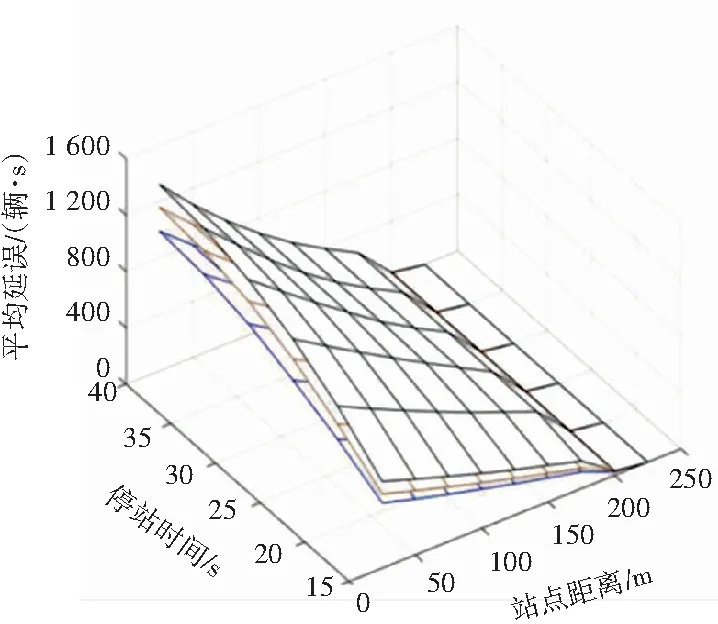
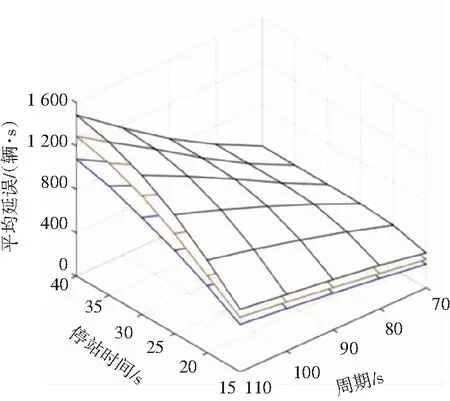
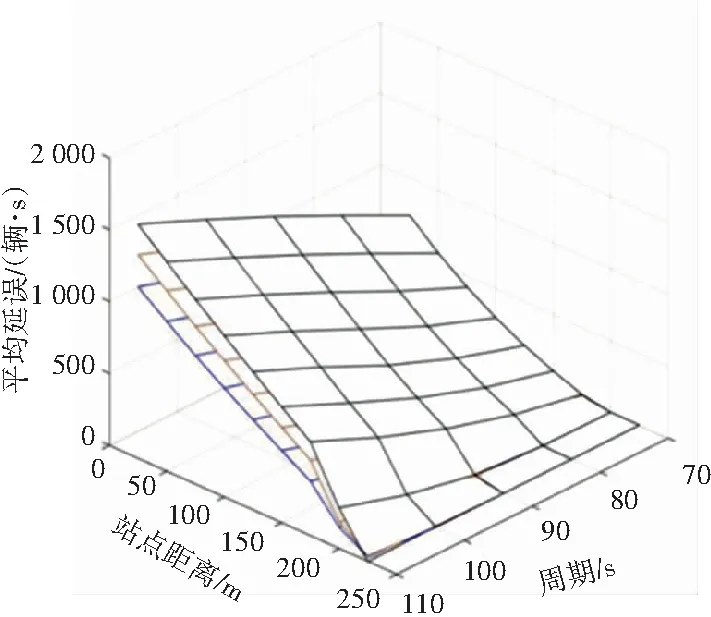
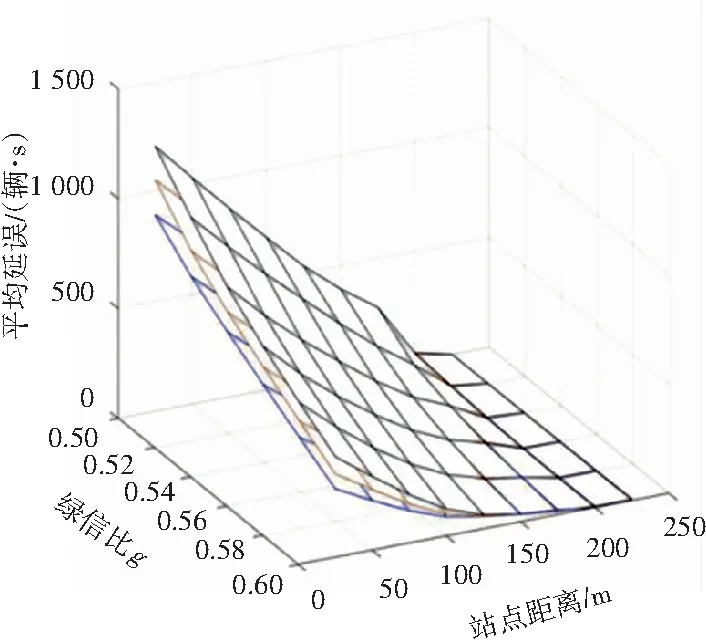
(1) 当X1 (7) (2)当X1 (8) (3)当X1≥gLc时,式(9)。 (9) (1)当X1 (10) (2)当X1 (11) (3)当X1≥gLc时,式(12)。 (12) 关于交叉口下游直线式公交站点的延误,在已知上侧和下侧两条曲线的解析式之后,通过计算,可以求得公交车在不同时刻进站所产生的不同交点的坐标,因此,延误可以通过定积分来计算,即由数学公式(13)来求解: (13) 本文通过一条公交站点位于交叉口下游的双向四车道路段,探讨在不同的变量条件下,包括站点距离、信号周期、交通流量、站点停留时间等对交叉口下游直线式公交站点的延误影响,并且通过MATLAB进行数值分析,基本输入见表1。数值分析时,假设只有一个变量发生变化,而其他变量值保持不变。表中第二列显示变量不变时的值,第三列是分析时变量的变化范围。 折减系数∂取不同值的情况下公交站点距离对社会车辆平均延误的影响,如图2所示。可以看出当∂越大时,延误呈整体下降的趋势,并且单条延误曲线也会随着距离的增加最终趋于零。本文结合交叉口处于欠饱和的状态下,为了后续参量变化范围的选择,这里取三组中间值∂=0.83、∂=0.85以及∂=0.87进行研究,通过设置周期时长、停站时间、站点距离以及绿信比的变化范围来对交叉口下游直线式公交站点处的车辆延误进行数值分析。 表1 数值分析参数 图2 不同折减系数∂下延误曲线 数值分析结果图3所示,分别表示为控制不同单一变量情况下研究另外二个变量的变化对交叉口下游直线式公交站点所造成的延误大小变化情况,由图3(a)可以看出在信号周期且绿信比为一定值时,延误是随着站点距离的增加而减少的,并且最终趋近于0,但是会随着公交车停站时间的增加而增加,同时当站点距离和停靠时间较小时,折减系数对于延误的影响就越大,反之就越小。当站点距离和绿信比保持不变时,延误也会随着信号周期的减少而降低,而当停站时间和信号周期越小时,折减系数对于延误的影响也就越小,反之就越大,如图3(b)。另一方面,由图3(c)可以看出当停站时间和绿信比为一定值时,平均延误会随着信号周期的增加而增加,同时折减系数的影响也就越明显。图3(d)表示当停站时间和信号周期为一定值时,平均延误也会随着绿信比的增加而减少,同时折减系数的影响也就越小,反之则越大。 (a) Lc=90 s, g=0.5 (b) d=70 m, g=0.5 (c) S=30 s, g=0.5 (d) S=30 s, Lc=90 s 数值分析结果说明了交叉口下游直线式公交站点受公交停靠所造成的车辆延误与站点距离、停站时间、信号周期以及绿信比都是有着直接关系的,任何一个参量的变化都会使得站点处延误发生改变。同时不同折减系数下车辆平均延误也会发生改变,会随着参量的改变产生或大或小的影响。因此,对于直线式下游公交站点而言,根据其上游交叉口的信号周期来选择合适的站点位置以及停站时间,以期达到公交停站造成的车辆延误最小的目标是非常重要的,或者从另一个角度出发,也可以根据已知公交站点的位置,结合路段的通行能力来设计合理的交叉口信号周期、绿信比以及公交车在下游站点的停靠时间。 本文针对交叉口下游直线式公交站点延误问题,建立了以交通流理论为基础的车辆延误计算模型,根据公交车进站时间和停站时间划分为6种情况进行分析,并通过MATLAB搭建仿真运行平台,同时根据站点距离,信号周期、停站时间等参量的变化范围来研究下游直线式公交站点处的车辆延误变化情况。结果表明,在不同折减系数下,延误会随着信号周期增加而增加,随着绿信比的增加而减少,同时当停站时间和信号周期越小或者绿信比越大时,折减系数对于延误的影响也就越小,反之则越大。本文分析结果为交叉口下游直线式公交站点的合理布局提供了一定的参考,即如何通过已知参量的信息来合理设置其它二个参量的范围以期达到车辆延误最小化的目标。但是,本文研究结果也存在一定的局限性,针对受公交车停站服务影响下的道路通行能力没有展开进一步研究,在后期还需要进行实地调查验证模型和折减系数标定的有效性。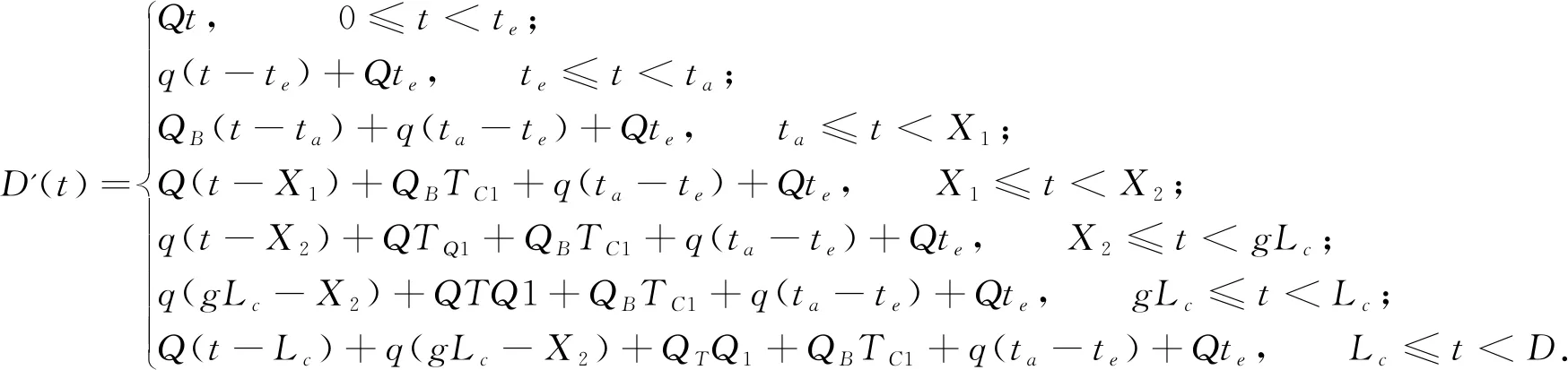
2 数值分析
3 结束语

