一道高考压轴选择题的多维赏析

周 春

(江苏省扬州中学 225009)

2017年高考全国卷Ⅰ选择题的最后一题(第21题)考查了高中物理一个常见的问题——动态平衡问题，但是，其解法并非都很常见，下面从多个维度对此题进行赏析.

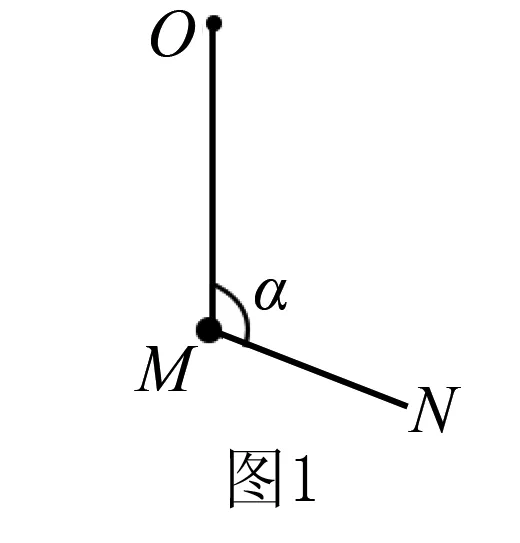
A.MN上的张力逐渐增大

B.MN上的张力先增大后减小

C.OM上的张力逐渐增大

D.OM上的张力先增大后减小

解析由题意可知，重物在变化过程中受重力G、绳MN拉力TMN、绳OM拉力TOM，在某一时刻受力分析示意图如图2所示.

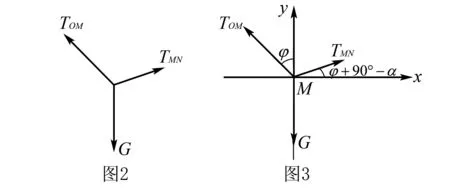
解法1 正交分解法

以M为原点，沿水平方向建立x轴，沿竖直方向建立y轴，如图3所示，设绳OM由竖直逆时针转过φ，则此时绳MN与x轴夹角为φ+90°-α(此式为负值时表示MN在x轴下方)，根据平衡条件得

TOMsinφ=TMNcos(φ+90°-α)，

TOMcosφ+TMNsin(φ+90°-α)=G.

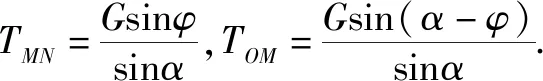
由于G和α均保持不变，而在OM由竖直被拉到水平的过程中，φ由0°缓慢增大至90°，故TMN由零逐渐增大.α-φ逐渐减小，且由钝角逐渐减小为直角再减小为锐角，故TOM先增大后减小(当α-φ=90°时，TOM最大).故选AD.

解法2 正弦定理法

将图2三个力平移为矢量三角形，并设力的矢量三角形的内角如图4所示.由正弦定理得

由于重力G的大小、方向均不变，两绳的夹角α不变，而图4中β=π-α，则β角也不变，故装置在逆时针缓慢转动过程中，上式比值为一定值.由题意得，γ由0°逐渐增大至90°，故TMN逐渐增大.又θ=α-γ，故θ逐渐减小，且由钝角逐渐减小为直角再减小为锐角，故TOM先增大后减小(当θ=90°时，TOM最大).

解法3 辅助圆法

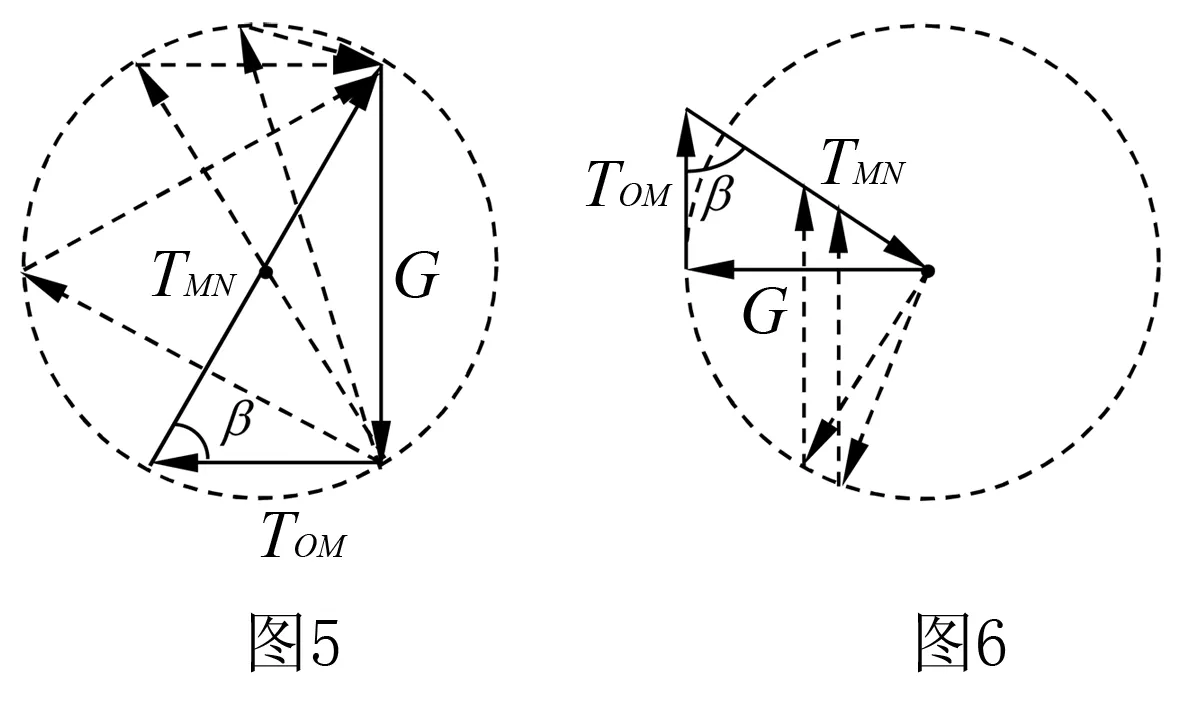
根据圆的性质可知，同一条弦对应的圆周角相等.而装置在逆时针缓慢转动过程中，由解法2分析可知，图4中G和β始终保持不变，故可以反推，图4中TMN、TOM连接点的运动轨迹必定是圆，且此圆即由TMN、TOM、G所构成的矢量三角形的外接圆，如图5所示(实线为末状态).初始状态，TMN=0，TOM=G.由图5可以直观看出，把整个装置逆时针缓慢转过90°的过程中，TMN从0逐渐变为直径，故TMN逐渐增大，TOM先从弦变为直径再变为弦，故TOM先增大后减小.

解法4 等效法

题中“将重物向右上方缓慢拉起，并保持夹角α不变.在OM由竖直被拉到水平的过程中”，可等效为“整个装置不动，把重力方向顺时针缓慢转过90°(重力大小不变)的过程中”，这样由“两个力方向在改变”转化为“只有一个力方向在改变”，问题得到了大大简化.显然，等效后的重力G矢量的箭头端的变化轨迹是以重力G的箭尾端为圆心、以重力G大小为半径的圆，作出TMN、TOM、G所构成的矢量三角形动态变化示意图如图6所示(实线为末状态).由于重力G的大小和β是定值，故由图6可以看出，在G顺时针缓慢转过90°的过程中，TMN逐渐增大，TOM先增大后减小(当G与TMN垂直时，TOM最大).

评析这是一道三力动态平衡问题，由于有两个力的方向同时在变化，而常用的合成分解法、相似三角形法等解法很难奏效，不少考生感觉难度较大，短时间内甚至束手无策，因此需要另辟蹊径.以上探讨了四种解法，从数学角度看，前两种解法属于代数法，后两种解法属于几何法，从解法1到解法4基本上越来越简便，而对于选择题这类“小题”，在考试时尽量不要“大做”，我们应倡导考生更善于应用后两种几何方法求解.

母题如图7所示装置，OQ杆竖直，OP杆水平，AC、BC两根轻绳拉住一球，其中AC绳水平.现保持两细绳间的夹角不变，若把整个装置顺时针缓慢转过90°，则在转动过程中，设AC绳的拉力为F1，BC绳的拉力为F2，下列说法中正确的是( )

A.F1先减小后增大 B.F1先增大后减小

C.F2逐渐减小 D.F2逐渐增大

启示上述母题是平时教学中曾经出现过但又不很常见的一道老题目，用前面四种解法均可解出答案为BC.显而易见，本高考题来源于上述母题，两题十分相似.因此，在平时的复习备考中，考生应全面夯实基础，努力提高分析问题、解决问题的能力，全方位掌握各种题型及其解法，既要对常见题型烂熟于心，也要对非常见题型刻骨铭心，这样应对高考时方能游刃有余.