放缩法证数列型不等式要“放缩得当”

叶文明 李 阳

(浙江省松阳二中 323406)

高考数学中，出现利用放缩法证明数列型的不等式，多以压轴题形式出现，需要综合利用相关知识与方法来解决问题.此类题型综合性强、形式复杂、运算要求高，能很好地考查考生的思维逻辑与处理信息的能力.在解题过程中，若能根据基本类型与结构特点，迅速找到方向，可取得事半功倍的效果.数列型不等式的放缩一般要借助不等式的性质、函数的单调性等进行放缩.

例(丽水2017学年期末监控)已知数列{an}满足a1=1,an+1=an+2n+1,{bn}是正项数列，且bn是an和an+2的等比中项.

(1)求数列{an}和{bn}的通项公式;

解(1)由累加法及已知条件易得an=n2,bn=n2+n.

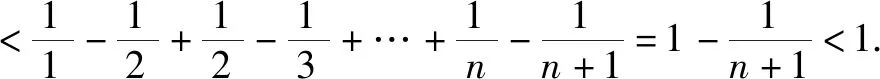
点评失败，失败原因是放缩过度，放得太大.

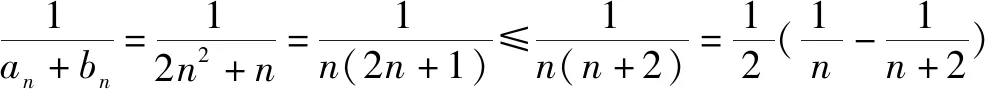
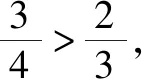
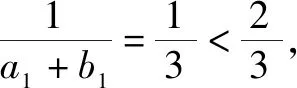
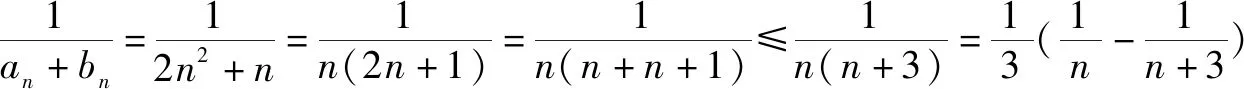
点评成功，放缩得当，命题得证.

解法四根据解法三可知，在解法三的基础上放得更小一点显然也能解决问题，如：

①当n=1和2时，不等式显然成立；

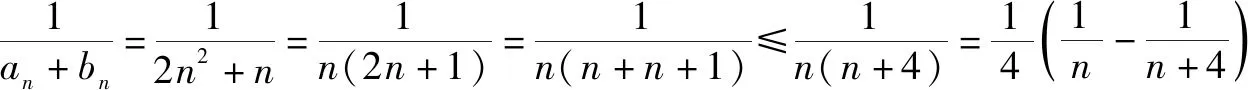
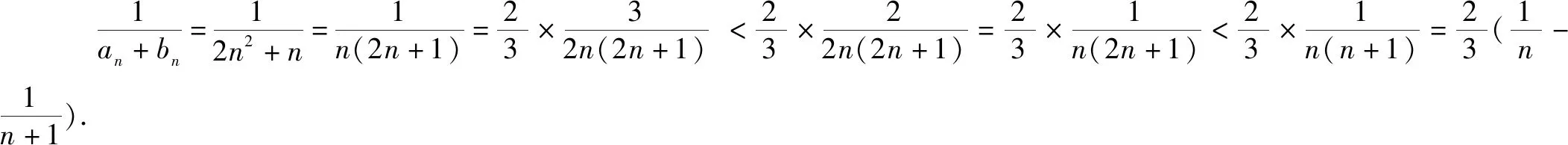
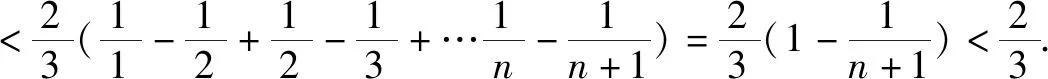
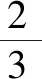
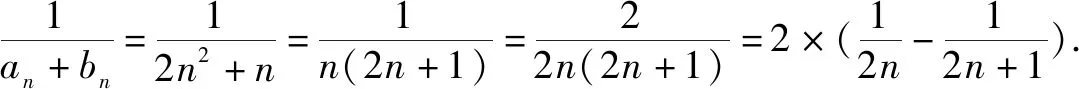
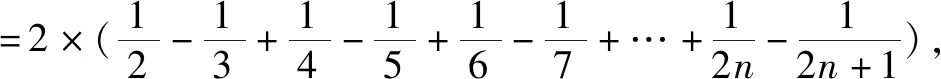
点评利用了对数函数的泰勒展开式，且2的自然对数值大于三分之二，将不等式进行放缩，使放缩结果趋近答案.

评析1.利用基本不等式进行放缩：①放缩应有“度”,不能太大，又不能太小；②要根据所证明的不等式的结构来选择所需的放缩方法;③放缩法有时需要多试验几次才能成功.

2.先求和再放缩：要先利用数列求和的方法求出数列的和，然后进行放缩；一般可利用裂项相消等方法进行求和，然后利用添减项的方法放缩.

3.先放缩再求和：可注意利用逐项进行放缩的方法，构造一个可求和的新数列，然后对这个新数列进行求和，构造的这个新数列可以为等比(差)数列，利用求和公式与裂项相消、分组求和等方法结合进行求和，然后利用添减项的方法放缩.

4.逐层递推放缩：这种方法要注意建立起相邻两项的相等或不等关系，利用逐层递推探求各项与首项之间的关系，从而可以建立一个新的数列.