解析几何中的数学思想赏析
黄光鑫 谢 超
(1.四川省成都市四川师范大学附属中学 610066;2.四川省成都市第二十中学校 610036)
数学思想是对数学事实与理论经过概括后产生的本质认识;基本数学思想则是体现或应该体现于基础数学中的具有奠基性、总结性和最广泛的数学思想,它们含有传统数学思想的精华和现代数学思想的基本特征,并且是历史地发展着的.
解析几何的创立在数学的发展史上具有里程碑的意义.学习解析几何不仅要学习各种不同题型的解答方法,更要透过灵活多样的方法,领悟其中蕴含的数学思想.
一、函数与方程的思想
函数思想就是利用运动变化的观点分析和研究具体问题中的数量关系,通过函数的形式把这种数量关系表示出来并加以研究,从而使问题获解.方程思想是从问题的数量关系入手,运用数学语言将问题中的条件转化为方程问题,然后通过解方程(组)使问题获解.函数与方程的思想既是函数思想与方程思想的体现,也是两种思想综合运用的体现,是研究变量与函数、相等与不等过程中的基本数学思想.
例1 已知抛物线C:x2=py(p>0)上点M处的切线方程为x+y+1=0.(1)求抛物线C的方程;(2)设A(x1,y1)和B(x2,y2)为抛物线C上的两个动点,其中y1≠y2,且y1+y2=2,线段AB的垂直平分线与y轴交于点T,求△ABT面积的最大值.


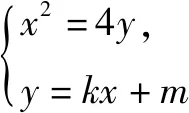

由Δ=16k2+16m>0得:k2+m>0.②
y1+y2=k(x1+x2)+2m=4k2+2m=2⟹4k2=2-2m.③


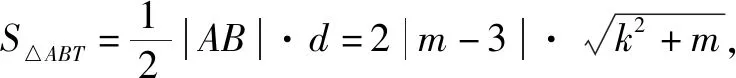
由4k2=2-2m>0得:m<1,将③代入②得:m>-1,∴-1 将③代入④得: 赏析本题将△ABT的面积表示为一个变量m的函数,随后就可以采用处理一般函数最值的常用办法(求导)去解决三角形面积的最大值问题. 整理得:2tx1-2y1+1=0.① 设B(x2,y2),同理可得2tx2-2y2+1=0. ② 于是x1+x2=2t,x1x2=-1,y1+y2=t(x1+x2)+1=2t2+1. 赏析本题第(1)问用变量的观点根据①式、②式以及方程的定义直接得出直线方程的方法值得借鉴!此题是利用变量的观点将两个变量统一到一个方程之中.变量是函数的基础,对应是函数的本质! (2)设两切线为l1,l2, ①当l1⊥x轴或l1∥x轴时,对应l2∥x轴或l2⊥x轴,可知P(±3,±2); ∴36k2-4[(y0-kx0)2-4]=0, 数形结合的思想就是充分运用“数”的严谨和”形”的直观,将抽象的数学语言与直观的图形语言结合起来,使抽象思维和形象思维结合,通过图形的描述、代数的论证来研究和解决数学问题的一种数学思想方法.数形结合思想是数学的规律性与灵活性的有机结合,通过“以形助数,以数辅形”,变抽象思维为形象思维,使复杂问题简单化,抽象问题具体化,有助于把握数学问题的本质,有利于达到优化解题的目的. (1)求椭圆C1的方程; 解法2 延长AD、BC交于点F,显然O为线段AB的中点,又因为OC∥AD,所以点C为线段BF的中点.因为AC是△ABF的中线,DE∥FB,从而点P为线段DE的中点.即|PD|=|PE|. 赏析解析几何本来就是数形结合的光辉典范!老一辈数学家华罗庚也曾经强调:“数形结合百般好,隔离分家万事休!”本题解法二充分挖掘图形的几何属性,数形结合,寻找数学美,巧添辅助线,如此机智的证明方法简直令人拍案叫绝! 分类与整合就是当问题所给的对象不能进行统一研究时,就需要对研究对象按某个标准分类,然后对每一类分别研究得出每一类的结论,最后综合各类结果得到整个问题的解答.分类与整合就是“化整为零,各个击破,再积零为整”的数学思想. 解(1)设椭圆长半轴长及半焦距分别为a,c,由已知得 当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆. 赏析本题第(2)问由于方程中参数取值的不确定性,因此需要进行详细的分类讨论.分类讨论实质上是把一个复杂的数学问题划分为若干个简单的数学问题各个击破!体现出化难为易,化繁为简的数学思维.分类讨论必需做到不重不漏! 化归与转化的思想是在研究和解决数学问题时采用某种方式,借助某些数学知识,将问题进行等价转化,使抽象问题具体化,复杂问题简单化,未知问题己知化等,进而达到解决问题的数学思想. (1)若|PF|=3,求点M的坐标; (2)求△ABP面积的最大值. “欲穷千里目,更上一层楼!”数学思想是数学的灵魂,只有对数学思想的透彻理解,深刻领悟,才能居高临下地看待问题,也才能找到更多、更好、更新的解法.
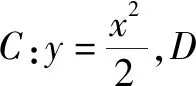
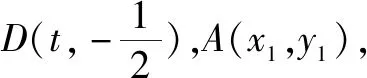

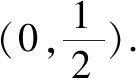
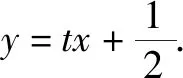
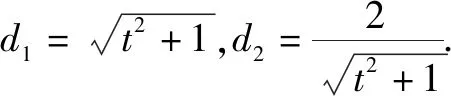
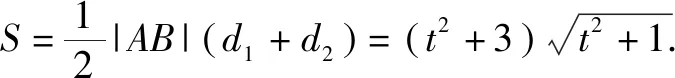
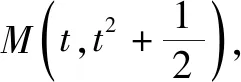


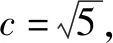





二、数形结合的思想








三、分类与整合的思想

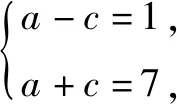
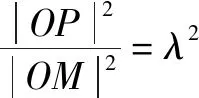

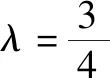
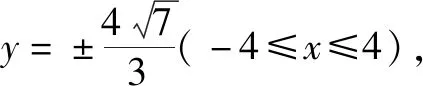

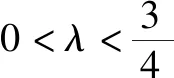
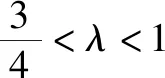
四、转化与化归的思想