应用力系简化原理求解分布力向任意一点简化问题的研究

董 茹，王小东

(1.榆林学院 建筑工程学院，陕西 榆林 719000;2.榆林学院 数学与统计学院，陕西 榆林 719000)

课程《工程力学》几乎是全国高校工程类专业必须开始的专业基础课，本人在教授本课程的同时，参考了大量的工程力学、材料力学等教材，对课本中的知识进行了深入的研究，力求提高教学能力，能让学生更好的理解一些难点或者复杂问题[1-2]。工程力学的所有教材中对于分布力等效于集中在分布长度中点的一个集中力这一问题，都是简单的一笔带过，学生也将其作为一个记忆性的知识点，就是单纯的记住。也未有文献对这一问题进行研究和说明。经过研究和思考，本文将提出将分布力等效于一个平行力系，利用高等数学微积分方法依托工程力学课程力系简化原理解决分布力向任意一心简化的复杂力学问题的思路，研究结果对于工程力学中分布力简化的问题具有很好的补充和解释。

1 《工程力学》课程的重要性

《工程力学》课程的理论性高、实践性强，是一门重要的工科专业基础课[3]。榆林学院作为培养应用型人才的本科院校[4]，开设工程力学课程的工科专业有建筑工程学院土木工程专业、给排水科学与工程专业等4个专业、生命科学学院水土保持、设施农业2个专业，还有能源工程学院的几个专业将近有数十个专业。工程力学课程作为所有工科专业必须开设的一门专业基础课，其重要性显而易见[5]。工程力学与建筑、石油化工、航天航空等很多领域的工程密切相关，包含的内容是很广泛的，不仅要培养学生扎实的基础理论知识，而且要培养学生的全面素质和创造能力[6-7]；工程力学教育不仅可以培养学生的力学素质，而且可以加强学生的工程概念，对于学生向其他学科或其他工程领域扩展是很有利的[8]。

在全国高校都在进行工程类专业工程教育认证的新形势下，创新人才培养模式、深入推进本科教育教学改革，深入开展工程教育专业认证势在必行[1]。工程教育认证中要求学生具有解决复杂问题的能力[2]，工程力学课程作为工科专业重要的专业基础课，在课堂教学中教师就要培养学生这方面能力的提升。因此在课程教学内容改革中也应考虑如何培养学生解决复杂问题的能力，本文以工程力学课程中分布力的简化这一复杂问题为研究对象，引导学生积极主动思考，运用所学知识解决复杂工程问题，最终利用高等数学微积分原理解决分布力向任意一点简化的复杂力学问题，期望能够达到工程教育专业认证要求，能够培养学生解决复杂工程问题的能力。

2 力系简化在工程力学课程中的重要性

力系简化是工程力学课程中非常重要的一部分内容，起到承前启后的作用。力系简化对静力学中静力学平衡方程的推导得出，以及材料力学中简化连续分布的内力系最终的得到6个内力分量[9]等问题都起到至关重要的作用。可以说，没有力系简化原理，工程力学中的很多问题都难以解决。所以，在课堂教授过程中，一定要让学生能够深刻的理解力系简化的过程、及简化的结果，同时要培养学生应用力系简化原理解决一些简单的甚至是复杂的力学问题以及实际工程问题的能力，学以致用。以下为课堂教学中此部分内容的教学改革的介绍，即应用力系简化原理求解分布力向任意一点简化的复杂问题。

3 应用力系简化原理求解分布力向任意一点简化的复杂问题

3.1 力系简化原理

3.1.1 力系简化的概念

所谓力系简化，就是将有若干个力和力偶所组成的力系，变成一个力或一个力偶，或一个力与一个力偶的简单而等效的情形。如图1所示，即将力F1、F2、F3、F4、F5以及力偶M向O点简化得到一个力FR和一个力偶M。

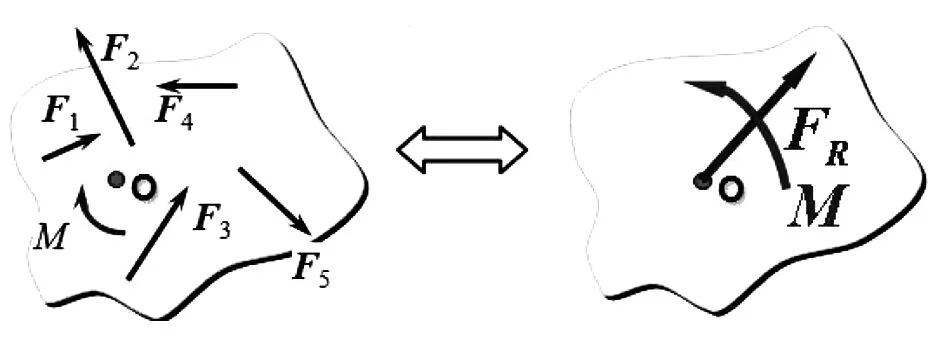
图1 平面力系简化

3.1.2 力系简化的基础是力向一点平移定理

作用在刚体上力的F，可以平移到其上任一点，但必须同时附加一力偶，力偶矩等于力对平移点之矩。如图2所示，将力F由作用点A平移至作用点B，但必须附加一个力偶，附加的力偶等于力F对B点之矩。在求证力向一点平移定理时用到了加减平衡力系原理。

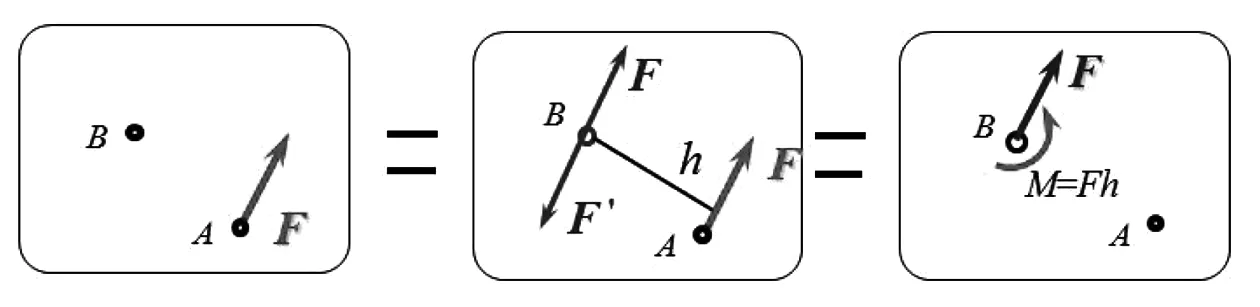
图2 力向一点平移

3.1.3 力系简化的结果

由力向一点平移定理，可以将平面力系向作用面内任意一点简化，一般情形下，得到一个力和一个力偶。所得力的作用线通过简化中心，这一力称为力系的主矢，它等于力系中所有力的矢量和；所得力偶仍作用于原平面内，其力偶矩称为原力系对于简化中心的主矩，数值等于力系中所有力对简化中心之矩的代数和。平面力系简化过程及结果如图3所示。

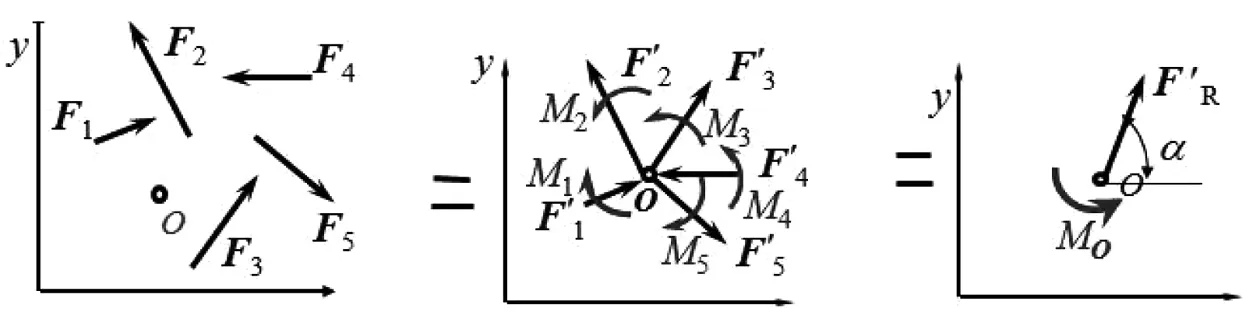
图3 平面力系简化过程及结果

3.2 应用力系简化原理求解分布力向任意一点简化的复杂问题

3.2.1 分布力的概念

如图4所示，桥面对桥梁的作用，接触面积比较大，力在整个接触面上分布作用，这时的作用力称为分布力，通常用单位长度的力表示沿长度方向上的分布力的强弱程度，称为载荷集度，用记号q表示，单位为N/m。

图4 分布力示意

3.2.2 分布力简化的关键难点问题

如图4所示的均布荷载，可以理解为作用在L长度上均匀分布着大小为q的力，q的大小为箭头长度、方向向下，作用点为L长度上的每一点，也可以理解为L长度上均匀分布的大小为q的无数个平行力系。因此，分布力简化的问题实则就是平行力系简化的问题，就是将无数个平行力所组成的平行力系向一点简化的问题，也就是将无数个平行力向一点平移的问题。那么这里面有两个非常重要的难点问题就是：其一是向哪一点去简化的问题，其二是如何解决无数个力平移的问题。如果能将这两个关键问题解决，那么分布力的简化问题就迎刃而解了。

3.2.3 应用高等数学积分的思路求解分布力简化的问题

针对以上提出的两个关键问题，采用数学微积分的方法解决无数个力平移的问题，同时，为了不将问题特殊化，将分布力向作用长度上的任意一点去简化，提高了问题的复杂性，力求所得结论的通用性。

如图5，建立数学模型：以分布力作用长度左端为坐标原点，以分布力作用长度所在直线为x轴，以分布力作用线所在方向为y轴方向。

分布力中无数个平行力q向L长度上任意一点C简化，定义C点距离坐标原点的距离为a，如下图5所示：

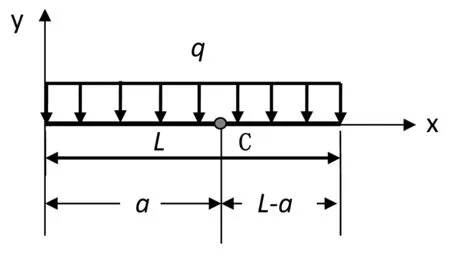
图5 建立数学模型

应用力向一点平移原理，将无数个大小为q的平行力向C点平移，同时附加无数个力偶，附加的力偶等于q对C点取矩。由于C点两侧的力向C平移时附加的力偶的转向不同，因此将L长度上作用的无数个q分成C点左侧(0≤x≤a)和C点右侧(a≤x≤L)两部分，最终简化的结果主矢为FR, 主矩为MC,，应用高等数学微积分的思路列式计算主矢和主矩分别为式(1)和式(2)。

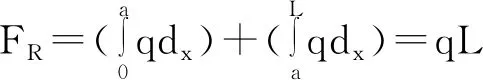
(1)

(2)

对上述结果进行讨论得出：分布力向任意一点简化的结果为：

可以看出，将分布力向作用长度的中点简化，所得结果只有主矢，没有主矩。这也就是课本中所说的分布力可以与作用在中点的集中力等效的原因。

4 总结

本文以《工程力学》课程中分布力等效于一个集中力这个课本中结论性的记忆知识点为研究，应用力系简化原理及高等数学微积分的方法求解分布力向任意一点简化的复杂问题，得出分布力向任意一点简化后的主矢和主矩的计算公式，并对所得公式讨论，最终解决了一个看似简单实则复杂的一类问题。在课堂中，这样讲解分布力简化的问题之后，发现学生表现出了极大的兴趣和探索精神，提高了学生学习的主动积极性，也得到了良好的教学效果，也达到了达到工程教育专业认证对培养学生解决复杂工程问题的能力的要求。