非规则铁路连续梁桥抗震体系优化

刘正楠，陈兴冲，张永亮，丁明波，刘尊稳

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

我国西部地区地震烈度高，地形地势复杂，非规则桥梁多，例如已建成的渝利铁路蔡家沟大桥、内昆铁路李子沟特大桥、宜万铁路姚家湾大桥、襄渝铁路牛角坪大桥等。正在规划筹建的川藏铁路大量也采用非规则桥梁结构[1]。在平面上，铁路桥梁的非规则性通过上部结构的布局形式来反映，如曲线桥等。在立面上，表现为相邻墩高的差异，这种非规则性造成的协同抗震性差、配筋困难、结构整体的抗震能力不明确及震后难以修复是桥梁抗震中的难题。

文献[2]中将板式橡胶支座、高阻尼橡胶支座及四氟滑板支座引入非规则公路桥梁的抗震中，发现合理的布置支座形式及参数取值，可改善内力分布，提高各墩的协同抗震能力，其原则可概括为“高墩增大支座刚度，矮墩减小支座刚度”。若矮墩高度低，有时还需增加支座刚度以“拉高”其墩底弯矩，使地震力分配均匀化[3]。因此，在某种意义上上述调整方法具有不确定性。目前，非规则铁路桥梁常采用减隔震以实现协同抗震，包括引入摩擦摆支座、黏滞阻尼器、Lock-up及减震榫等减隔震装置[4-7]。但是研究表明，铁路桥梁中减隔震装置适用的局限性较大，以矮墩为主。我国现行《城市桥梁抗震设计规范》[8]指出一联内桥墩刚度相差较大时，宜在各墩墩顶设置合理剪切刚度的橡胶支座，来调整各墩的等效刚度。《公路桥梁抗震设计细则》[9]指出相邻桥墩高度相差较大导致刚度相差较大的情况，宜在刚度较大桥墩处设置活动支座或板式橡胶支座。《铁路工程抗震设计规范》[10]中把相邻桥墩高度相差较大作为桥梁采用减隔震设计的适用条件之一。美国ASSHTO[11]及CALTRANS规范[12]中仅从结构形式及参数方面对非规则桥梁进行了界定，但明确指出该规范仅适用于规则桥梁。从规范及文献可以看出，非规则桥梁的抗震设计方法较为笼统、模糊，可操作性较差，对抗震性能具体应达到何种程度未明确指出。但受地形地势影响，山区非规则桥梁墩柱一旦在地震中发生破坏或损伤，其震后修复难度很大。因此，非规则桥梁合理的抗震体系应兼顾抗震性能与震后修复两方面，使其达到“大震不坏”的设防目标。

为此，本文以西部山区1座非规则铁路连续梁桥为研究对象，建立全桥有限元分析模型，将摇摆隔震及支座减隔震引入该类桥梁的抗震体系中，系统的探讨了非规则铁路连续梁桥采用摇摆隔震的合理性及支座减隔震时桥墩的优化配筋方法，以优化非规则铁路桥梁的合理抗震体系。

1 研究对象

跨径布置为(60+100+60)m预应力混凝土连续梁桥，上部结构为单箱单室变高度变截面直腹板箱梁，梁顶宽12.6 m，底宽6.7 m。中支点梁高7.85 m，跨中及边跨直线段梁高4.85 m，梁底下缘按2次抛物线变化。下部结构为矩形实心桥墩、群桩基础，其立面布置如图1所示。3#墩为制动墩，墩底截面尺寸横桥向为12 m，纵桥向7 m，墩身及承台均采用C30混凝土，普通钢筋采用HRB335。二期恒载为140 kN·m-1。

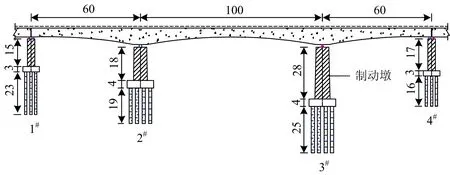
图1 全桥立面布置图(单位：m)

2 有限元模型及地震动输入

2.1 有限元模型

采用Sap2000建立有限元模型。主梁、桥墩及承台均采用梁单元模拟，二期恒载以均布质量的形式施加于主梁，桩土相互作用采用六弹簧模拟并施加于承台底，邻跨影响以节点质量形式施加于边跨墩顶。普通支座采用主从约束模拟，摩擦摆支座采用双线性单元模拟，其滞回曲线如图2所示。图中：Ki为滑动前初始刚度；K为屈后刚度；μ为摩擦系数；W为支座所受竖向荷载；Dy为初始滑动位移。

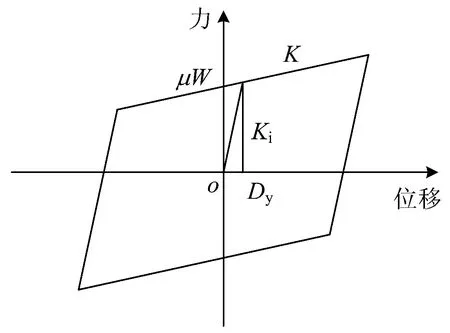
图2 摩擦摆支座滞回曲线

2.2 地震动输入

桥址位于8度地震区，设计地震加速度峰值0.2g(g为重力加速度)，罕遇地震加速度峰值0.38g。基于美国太平洋强震数据库(PEER)选取3条实测地震记录El-centro波(1940年)、San Fernando波(1971年)及Taft波(1952年)，见表1。并依据设计地震、罕遇地震分别将加速度峰值调至0.2g和0.38g。顺桥向输入进行非线性时程分析，计算结果取3条波的平均值，时程曲线结果仅列出3条波计算的最大值。

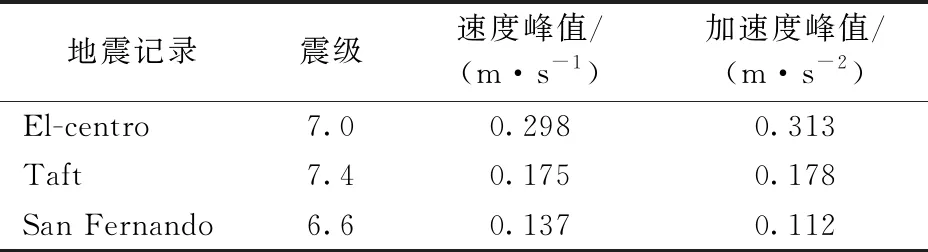
表1 地震波

3 非规则桥梁抗震体系优化

3.1 分析工况

本文建立3种工况进行分析。工况1：传统抗震，3#墩采用盆式固定支座，其余各墩采用盆式活动支座。工况2：摇摆隔震，3#墩设为摇摆隔震墩，墩底设置提离加台，尺寸横桥向15 m、纵桥向10 m、高2 m，并在原承台四周设置2 m高的混凝土挡块，限制提离桥墩的滑动，支座布置形式与工况1一致，摇摆桥墩如图3所示。工况3：支座减隔震：全桥采用摩擦摆支座，优化桥墩配筋。

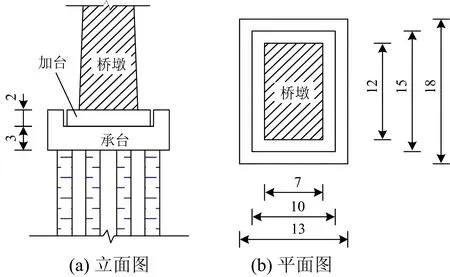
图3 摇摆桥墩(单位：m)

3.2 传统抗震

采用传统抗震，计算模型考虑2种情况：①制动墩保持弹性；②制动墩可进入弹塑性，其配筋率取1.2%，墩底设塑性铰，采用Takeda模型模拟。其中制动墩弹性计算是用以后文减震效果的分析，制动墩弹塑性计算是用以计算延性需求(曲率)，初步判断延性体系桥墩的损伤。

当制动墩保持弹性时，罕遇地震下结构的地震响应见表2。由表2可以看出：活动墩墩底弯矩仅为制动墩的5%～10%，墩底剪力仅为制动墩的10%～20%，各墩之间无法合理进行地震力的分配，造成制动墩受力过大。

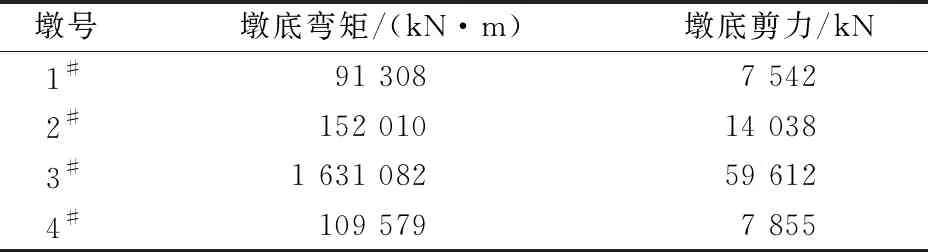
表2 工况1地震响应

当制动墩可进入弹塑性时，3#墩在罕遇地震下发生屈服，墩底曲率14.03×10-3rad·m-1，墩底屈服曲率8.14×10-4rad·m-1，接近桥墩极限曲率16.87×10-3rad·m-1，桥墩发生了较大的塑性转角，损伤严重。可见，考虑山区桥梁桥墩震后难以修复等问题，采用延性体系存在明显的不妥。

3.3 摇摆隔震

为实现“大震不坏”的设防目标，提出非规则连续梁桥的摇摆隔震体系，考虑如下因素。

(1)结构特点：根据参考文献[13]，铁路桥梁中的高墩、中等高度桥墩及矮墩界定的大致范围分别为大于30，20～30和20 m以下，本文背景工程中，制动墩(3#)为中等高度桥墩，其余各墩均属于矮墩的范围。高墩通常为空心墩，矮墩及中等高度桥墩常为实心墩，本文3#墩为实心桥墩。

(2)受力特征：梁体质量大，惯性力大。制动墩(3#)为非规则桥中的较高的桥墩，墩身自重大，加之上部梁体传递的竖向力，墩底恒载轴力达到109 MN，在加台尺寸一定的情况下可有效提供抗提离弯矩来抵消上部结构产生的较大惯性力。

(3)变形特征：由于墩底恒载轴力较大，抗提离弯矩也较大，在确保设计地震与罕遇地震可提离的前提下，桥墩能有效控制提离位移及墩顶位移。

对于工况2，首先进行多遇地震下的抗震设计，摇摆桥墩要求正常使用及多遇地震下不发生提离。此状态与传统非提离桥墩一致，依据《铁路工程抗震设计规范》[10]进行小震不坏的验算，验算的内容包括基底合力偏心距、基础抗压强度与稳定性验算(滑动稳定系数取1.1，倾覆稳定系数取值1.3，摩擦系数f取0.6)。验算结果如下。

合力偏心距e=2.77 m<2γ=4.96 m(γ为基础底面计算方向上的核心半径，具体取值为2.88 m)。

抗滑移、抗倾覆的摩擦力1.1Q=12 207.8 kN<[Q]=0.6×109 279=65 567.4 kN。其中，Q为扩大基础实际剪力；[Q]为最大容许抗滑移摩擦力。

抗滑移、抗倾覆的抗倾覆力矩1.3M′=394 755.4 kN<[M]=5×109 279=546 395.1 kN·m。其中，[M]为最大容许抗倾覆弯矩。

由此可得结构能满足小震不坏的抗震设防要求。

设计地震及罕遇地震作用下，采用双弹簧模型模拟桥墩的提离摇摆[14]，提离弹簧只考虑受压不考虑受拉，分析模型如图4所示。

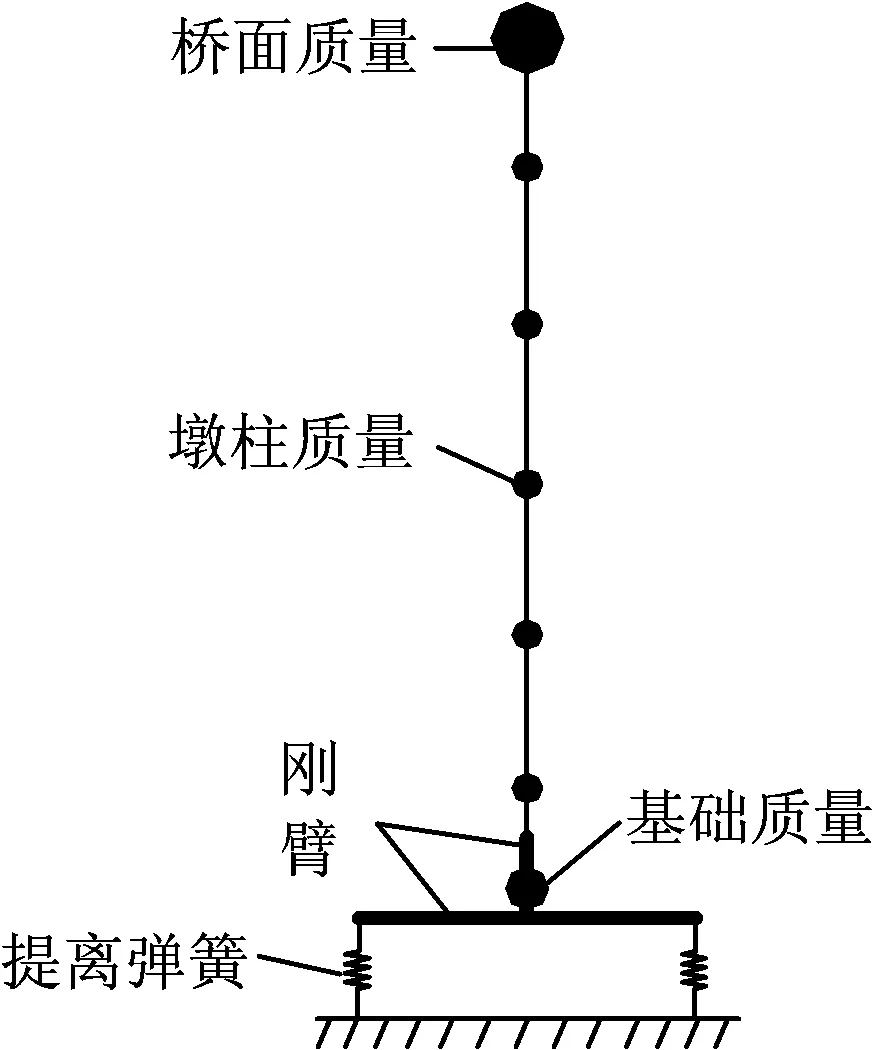
图4 分析模型

桥墩保持弹性，采用式(1)计算得到每端承压弹簧刚度为4.32×108kN·m-1。

(1)

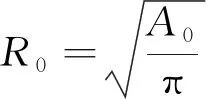
式中：Kv为竖向刚度；R0为等效半径；A0为扩大基础的截面积；G和v分别为基础材料的剪切模量和泊松比。

设计地震作用下，桥墩发生了提离。图5仅给出El-centro波对应的提离位移时程曲线，由图5可见，提离位移约为0.02 m，符合摇摆桥墩的隔震理念。

罕遇地震下，结构的地震响应见表3。图6给出了制动墩墩底弯矩时程曲线。

由图6可见：制动墩采用摇摆隔震后，内力需求大大减小，墩底最大弯矩控制在±625 MN·m之间。由表3可知：墩高相差不大的各活动墩的墩底弯矩相差不大。由此构成的抗震体系转延性抗震体系中配筋需求较高的3#墩为摇摆墩，且提离后墩底弯矩变化稳定，不主导整个结构的地震内力分布，若对其进行合理配筋使得在大震下保持弹性，易与其余各墩形成协同抗震体系。

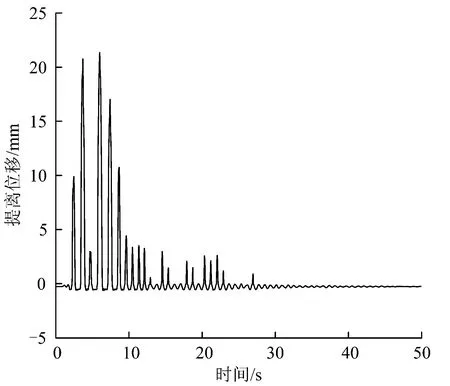
图5 提离位移时程

表3 工况2地震响应

墩号墩底弯矩/(kN·m)墩底剪力/kN1#101 5878 4072#174 45315 1993#625 10337 6794#112 0207 976

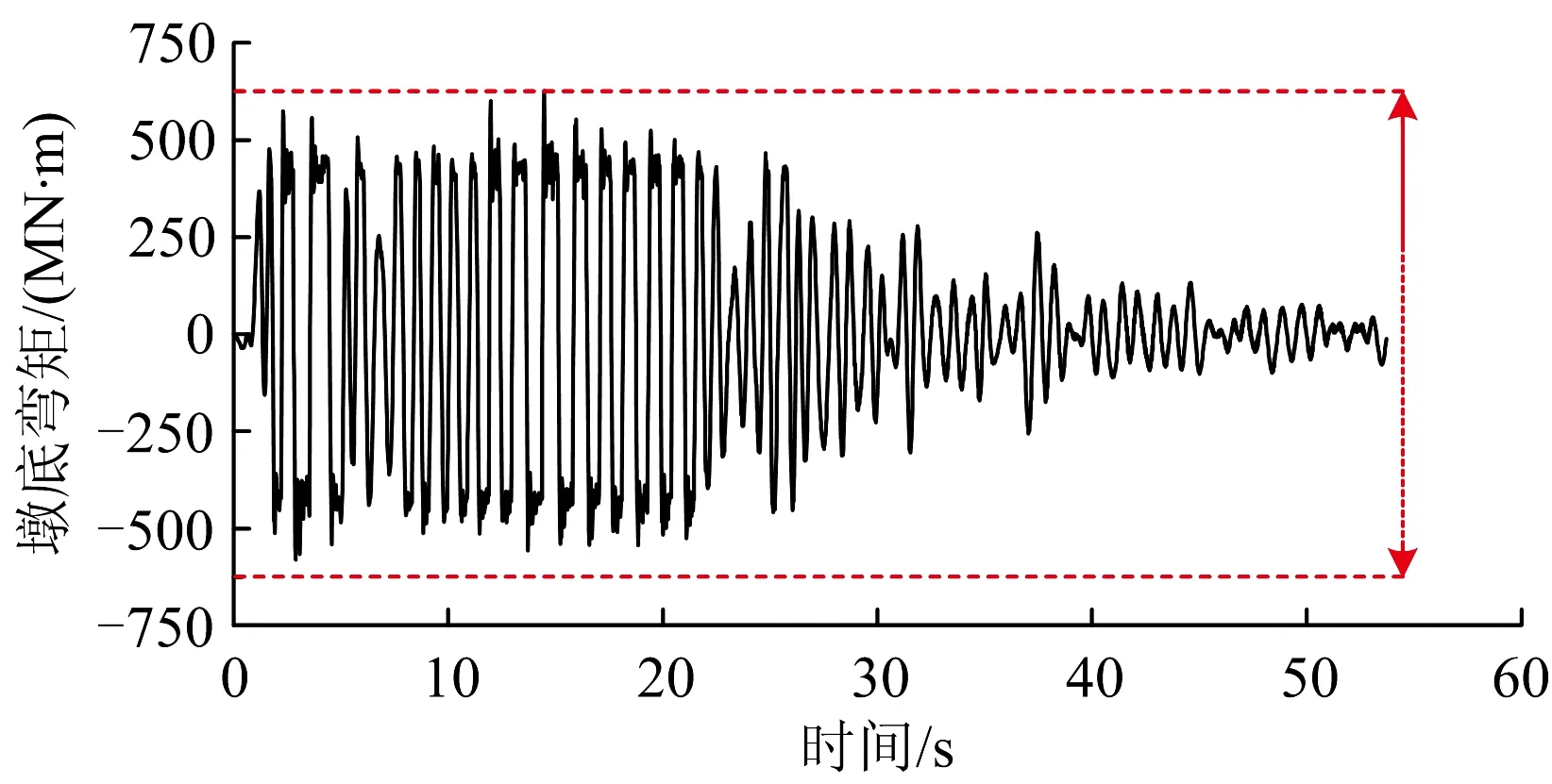
图6 制动墩墩底弯矩时程曲线

罕遇地震作用下，摇摆墩墩顶位移为12.8 cm，较好实现了力与位移的平衡。然而，与文献[13—14]相比，其墩顶位移相对较小。引起这种现象的主要原因分析如下：①与既有文献相比，本文研究对象桥墩为中等高度重力式桥墩，既有文献以空心高墩为对象；②既有文献，墩高、空心及墩底的限位措施均会使高墩墩身在提离摇摆的过程中发生相对显著的弯曲变形，墩顶位移的放大效应更为明显；③恒载作用下，中等高度桥墩相比高墩或矮墩均具有较大的墩底轴力，当墩底弯矩需求一定时，中等高度桥墩往往会以较小的提离位移满足墩底内力需求(位移敏感程度高)，相应的会产生较小的墩顶位移，如图7所示。因此非规则桥梁的摇摆隔震不需要特殊的限位装置，其设计简易方便。

对摇摆桥墩进行抗震性能验算，取摇摆墩的配筋率为0.6%，计算结果见表4。由表4可以看出，混凝土的最大压应力小于15 MPa，钢筋的最大拉应力小于335 MPa，由此表明，墩底处于弹性工作状态，在罕遇地震下，结构保持“大震不坏”的设防水平，与传统延性抗震相比，配筋率降低了50%。

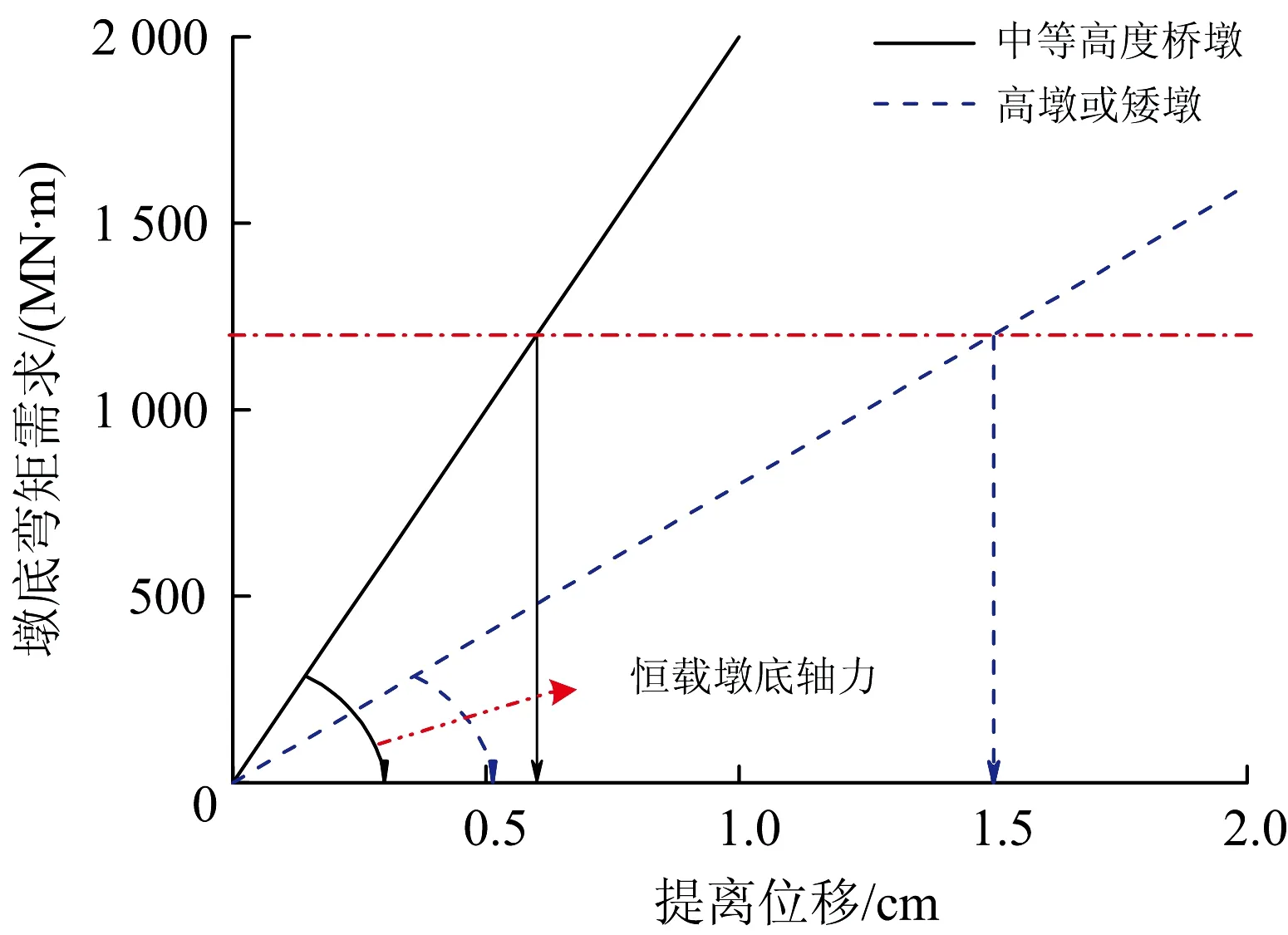
图7 提离位移与墩底弯矩需求的关系

表4 3#墩抗震性能验算结果

地震强度配筋率/%混凝土最大压应力/MPa普通钢筋最大拉应力/MPa0.38g0.612.9319.6

3.4 支座减隔震

全桥采用摩擦摆支座进行减隔震分析，选取摩擦摆式减隔震支座滑动曲面的曲率半径R=5 m和摩擦系数0.05，考虑支座非线性对结构进行时程分析。计算结果见表5。

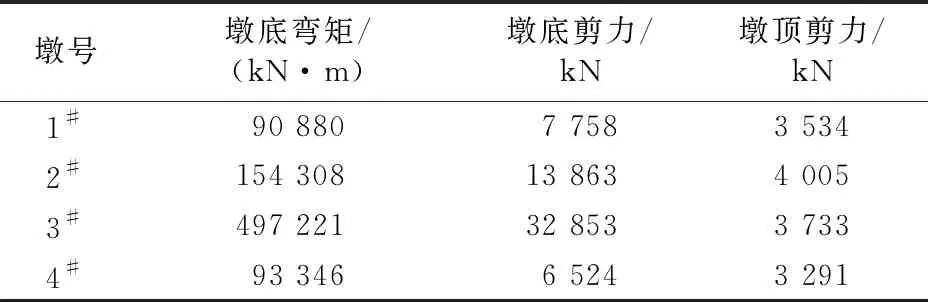
表5 工况3地震响应

由表5可以看出：制动墩墩底弯矩从传统抗震的1 631 MN·m降低到摇摆隔震的625 MN·m，再到摩擦摆支座减隔震的497 MN·m，降幅最大达到69%；罕遇地震下，各支座均已进入非线性隔震耗能，梁体惯性力的分配也相对均匀，各墩墩顶剪力在3 000～4 000 kN之间变化；通过对比2#与3#墩发现，墩顶惯性力相近，墩高增加了10 m，墩底弯矩却放大了2倍多。为探究其原因，对墩底弯矩的影响因素进行分离，定义墩身地震反应贡献率η=(墩底弯矩值-墩顶剪力值×墩高)/墩底弯矩值。计算发现对于本文研究的非规则铁路连续梁桥，各墩墩身地震反应贡献率相差较大，其中制动墩墩身地震反应的贡献率为71%。可见采用减隔震后，墩底弯矩的控制因素为墩身惯性力，这是由于铁路中等高度重力式桥墩自振频率较高，地震反应大，采用支座减隔震亦无法有效调整各墩受力状态，使其协同抗震，故需进一步对采用减隔震支座时的桥墩配筋进行优化研究，以期各墩同时保持弹性，避免个别桥墩率先进入塑性出现损伤。

鉴于此，提出采用摩擦摆支座的非规则铁路连续梁桥桥墩配筋优化准则，可表达为

Ms(1)∶Ms(2)∶Ms(3)∶Ms(4)

=M(1)∶M(2)∶M(3)∶M(4)

(2)

式中：Ms为墩底屈服弯矩；M为墩底实际弯矩；1—4代表墩号。

具体实施步骤如下。

①假定桥墩保持弹性，计算墩底轴弯时程。

②建立系列配筋率下的桥墩轴力—弯矩曲线。

③依据轴弯时程与轴力—弯矩曲线的包络关系，确定各墩最小配筋率。

按照以上步骤，图8为1#与3#墩的轴力—弯矩曲线与轴弯时程关系曲线。所确定桥墩的最小配筋率，见表6。

4 结 论

(1)考虑到非规则桥梁的震后修复难度较大，建议提高其设防水平，通过对抗震体系合理优化达到“大震不坏”的抗震性能要求。

(2)当非规则连续梁中中等高度桥墩(制动墩)为摇摆桥墩时，大震下墩底内力减小，具有提离后墩底弯矩变化稳定的优点。同时由于墩底恒载轴力较大，可较好的控制墩顶位移，对其进行合理的配筋，可达到“大震不坏”的设防水平，由此构成的减隔震系统易实现协同抗震。

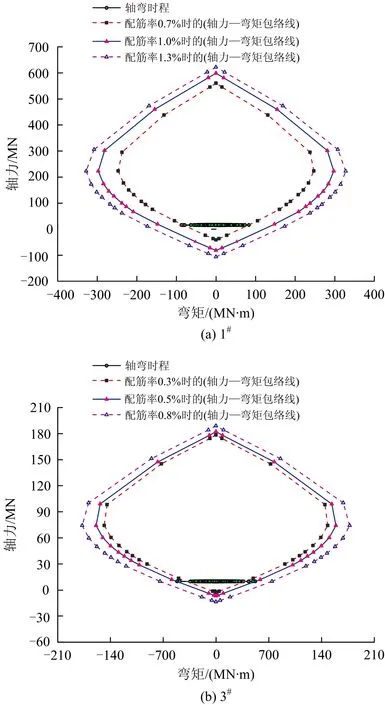
图8 轴力—弯矩包络线

表6 各桥墩的配筋率

墩号1#2#3#4#配筋率/%0.70.30.50.7

(3)采用支座减隔震的非规则桥梁中，墩身对墩底弯矩贡献率可达70%，以各墩屈服弯矩比恒等于墩底实际弯矩比为优化准则确定桥墩配筋的方法合理可行，可达到预期的效果。