基于车辆响应的高速铁路周期性轨道短波病害时频特性分析

晏兆晋，高翠香，徐晓迪，刘金朝，孙善超

(1.中国铁道科学研究院集团有限公司 铁路基础设施检测中心，北京 100081； 2.北京交通大学 远程与继续教育学院，北京 100044； 3.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081)

高速铁路周期性轨道短波病害主要包括打磨痕迹和钢轨波磨。统计结果表明，高速铁路打磨痕迹波长一般分布在30～100 mm之间，钢轨波磨波长一般分布在40～200 mm之间。在高速运行环境下，钢轨波磨容易造成轨道—车辆系统剧烈的高频振动，增加轨道—车辆系统的结构损伤。

为了有效诊断高速铁路打磨痕迹和钢轨波磨，国内外学者做了较多的研究工作。SUNAGA Y等[1]提出利用轴箱加速度评判轨道短波不平顺。SUDA Y等[2]提出了利用车辆轴箱垂向加速度检测钢轨波磨的方法，通过使用小波分析，可以准确地对钢轨波磨进行定位；并利用连续小波变换研究钢轨波磨的发展规律[3]。CAPRIOLI A等[4]利用小波从轴箱加速度中提取轨道短波不平顺的频率特征。邓小军等[5]利用改进HHT方法提取了在波磨激励下轨道—车辆耦合系统中车辆系统的瞬态响应特征，并指出钢轨波磨会引起车辆系统的振动响应频率调制。可见，轴箱加速度等车辆动态响应信号在钢轨波磨的检测分析中起了重要的作用，然而目前利用车辆动态响应信号进行打磨痕迹的相关研究却较少。

打磨痕迹和钢轨波磨的研究依赖于对车辆动态响应信号的时频分析，但是最终能够支持钢轨波磨诊断的是振动信号中的瞬时频率特性。瞬时频率(Instantaneous Frequency, IF)是对非平稳信号特征的有效描述，目前在各种通信信号、探测信号中均有所应用。集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)方法通过自适应的筛选将信号分解为多个固有模函数(Intrinsic Mode Function, IMF)，并对分解后的各IMF进行Hilbert变换[6]，得到相应的瞬时频率，但是该方法缺乏严格的数学证明。由经典的Fourier变换发展起来的短时Fourier变换(STFT)是1个时频分析的工具，但是在时频局部化的精细方面和灵活方面欠佳。DAUBECHIES I.等[7]提出的同步压缩小波变换(Synchro-Squeezed Wavelet Transform，SST)，是1种时频谱(TFR)上的重排算法，它一个有力的优点是支持信号重构，从而使得时频谱上的频率曲线更清晰。

本文对基于SST的瞬时频率提取方法进行改进(以下简称为改进方法)；以解析信号为例，将采用SST方法得到的时频谱以及采用改进方法提取出的瞬时频率曲线与EEMD-Hilbert变换方法和Wigner-Ville 分布(WVD)方法进行对比验证。选取基于高速铁路综合检测列车轴箱振动加速度检测数据，采用改进方法，得到综合检测列车经过留有打磨痕迹和波磨区段的轴箱振动加速度信号的时频响应特征；通过对动、静态数据的分析，以及对轮轨系统各部件固有频率的挖掘，得到打磨痕迹与钢轨波磨之间的频率响应关系，探索轮轨系统的非线性振动特性以及高速铁路打磨痕迹对钢轨波磨形成的影响。

1 基于SST瞬时频率提取方法的改进

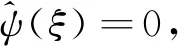
由于在进行时频重排时，需要计算相位，如果小波变换结果|Wf|≈0，相位会非常不稳定，所以需要设定1个硬阈值γ[8]，利用该阈值，规定相位的支集为

m=0，…，n-1

(1)

其中，

aj=2j/nvΔtj=1，…，Lnv

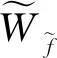
SST方法在瞬时频率成分的分离方面有很大的优势，然而，分离的结果是在频率脊线走势不连续时，由于提取阈值的设定，将原本属于同一条频率脊线的成分分离成了多个片段，使得对瞬时频率变化规律的研究有诸多不便。因此，提出以下改进的基于SST的瞬时频率提取方法，将频率脊线尽量提取成为数量较少而且连续的曲线。改进的算法流程如图1所示。

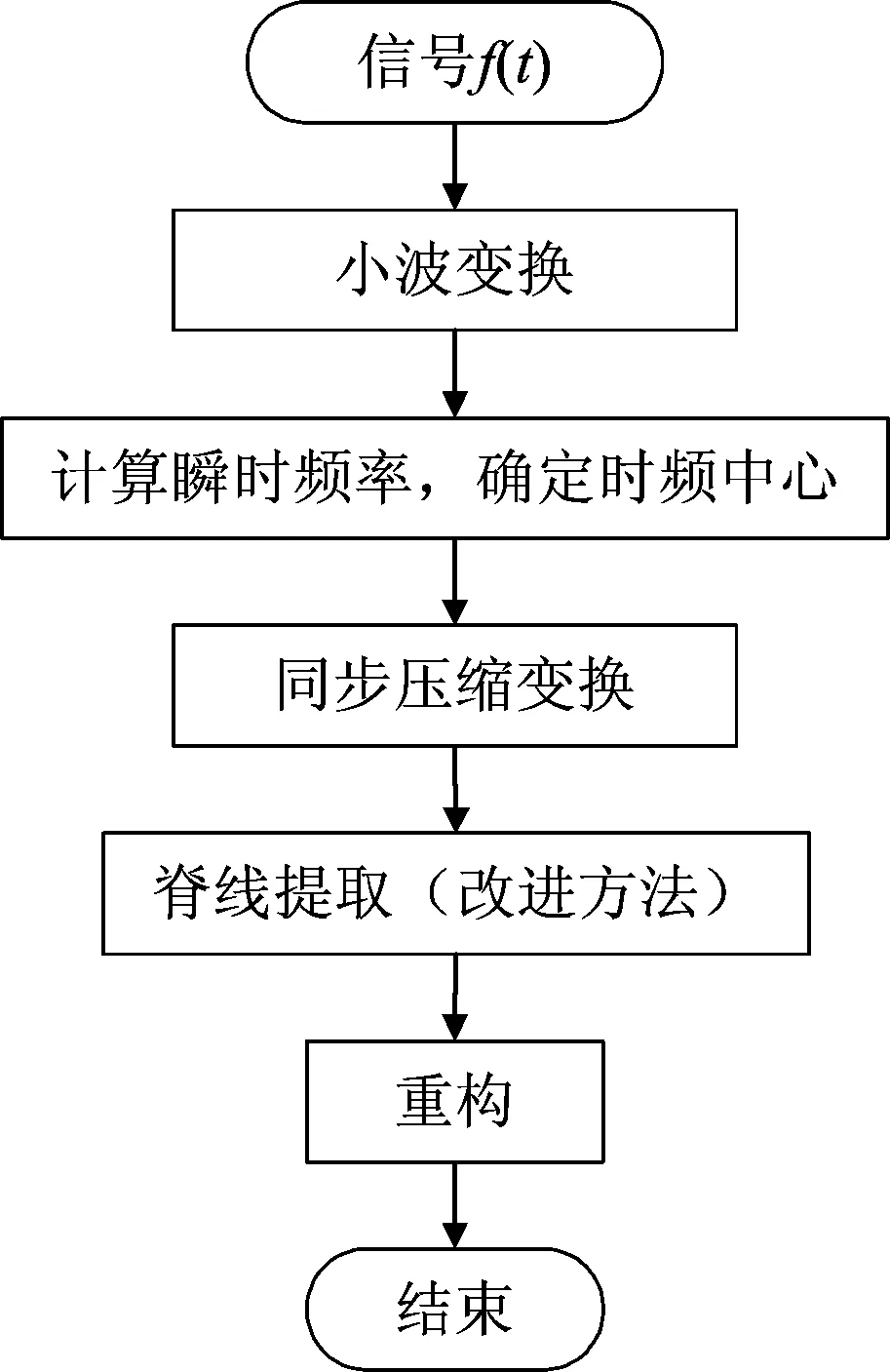
图1 改进的基于SST的瞬时频率提取算法流程图

改进的基于SST的瞬时频率提取算法步骤如下。

第1步：令频率曲线数量编号k=1且为有限值。

第2步：找到能量最大点对应的时频曲线，记为Ck，并记能量最大点频率为f0，时间为t0。

第3步：令时间半径为t′，频率半径为f′，在时间—尺度TF平面上，最小时间为ts，最小频率为fs，最大时间为te，最大频率为fe，取tmax=min{t0+t′，te}，fmax=min{f0+f′，fe}，tmin=max{t0-t′，ts}，fmin=max{f0-f′，fs}，则他们分别为频率曲线Ck对应的起始时间和频率、截止时间和频率。

第4步：计算[tmin，tmax]×[fmin，fmax]区域内能量之和S， 判断S是否大于γ。

①若S≥γ，则将[tmin，tmax]×[fmin，fmax]区域内的能量保存在Ck对应的区域中；并在原来的TF平面上，将该区域的能量置为0；

②若S<γ，则将Ck的TF平面以及原TF平面上对应[tmin，tmax]×[fmin，fmax]区域的能量均置为0。

第5步：向左移动1个点，并置时间t0=t0-1，更新tmin和fmin。若t0=0或者t0=te，则转第6步；否则，转第2步。

第6步：k=k+1。若剩余区域能量不小于γ，则转第2步；否则，算法终止。

上述算法保证了提取的频率曲线的完整性，参数k的变化保证了TF平面上各不同的频率曲线都能提取出来。根据SST变换理论[7]可知，有限带宽信号是可以被重构出来的，而且每1条频率曲线对应的信号在每1个时刻的频率是单一的。

2 方法验证数值试验

2.1 解析信号的时频谱与瞬时频率曲线提取

以解析信号f(t)为例进行分析， 其由f1(t)和f2(t) 2部分组成，t从0到10变化，表达式为

f(t)=f1(t)+f2(t)

(2)

其中，

解析信号的原始波形以及分别通过小波变换和SST所得到的时频谱如图2所示。对比图2中图(b)和图(c)可以看出，SST计算时频的聚集性更好。

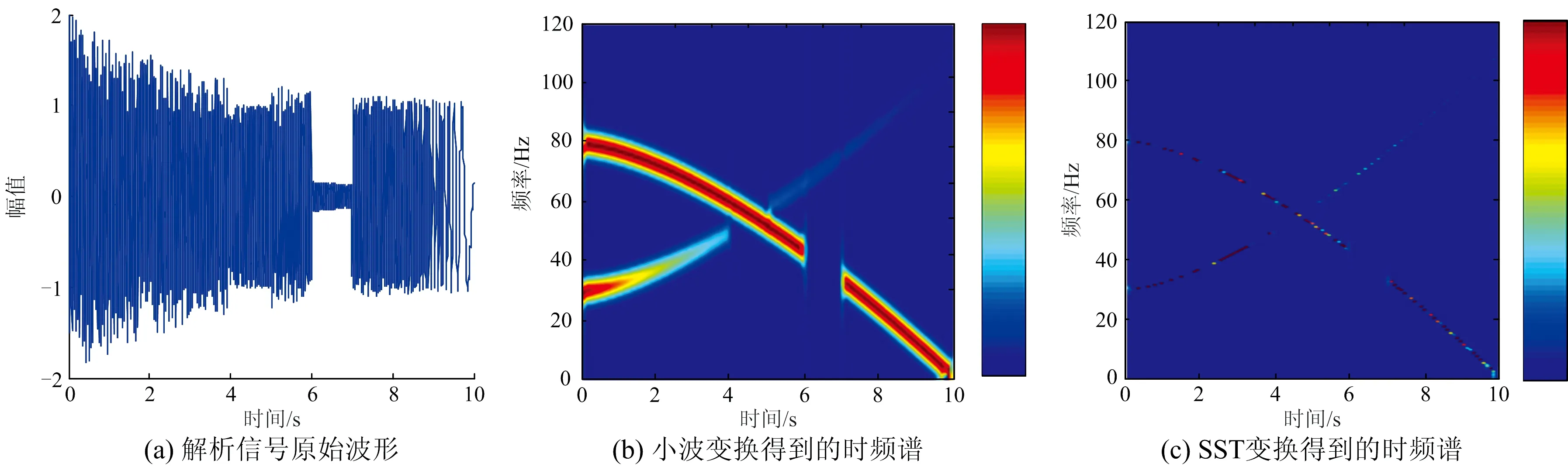
图2 解析信号原始波形及时频谱

由于阈值的设定，导致时频谱上的频率曲线不连续，图3为利用SST分离出的4个IMF及其对应的瞬时频率曲线。其中图(a)和图(e)原本属于同一个IMF，图(c)和图(g)原本属于同一个IMF，但是他们分别在第6～7 s以及第4～5 s被分开了。而利用改进方法提取的信号则相对连续，各个成分分别如图4的图(a)和图(c)所示。图4的(b)和(d)为各个成分对应的瞬时频率的解析值和提取值，通过比较可以发现，提取值的精确度比较高。需要指出的是，在曲线的起始和结束处的震荡是由边界效应引起的。

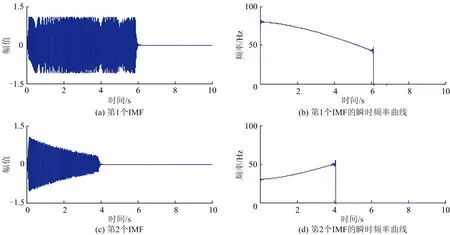
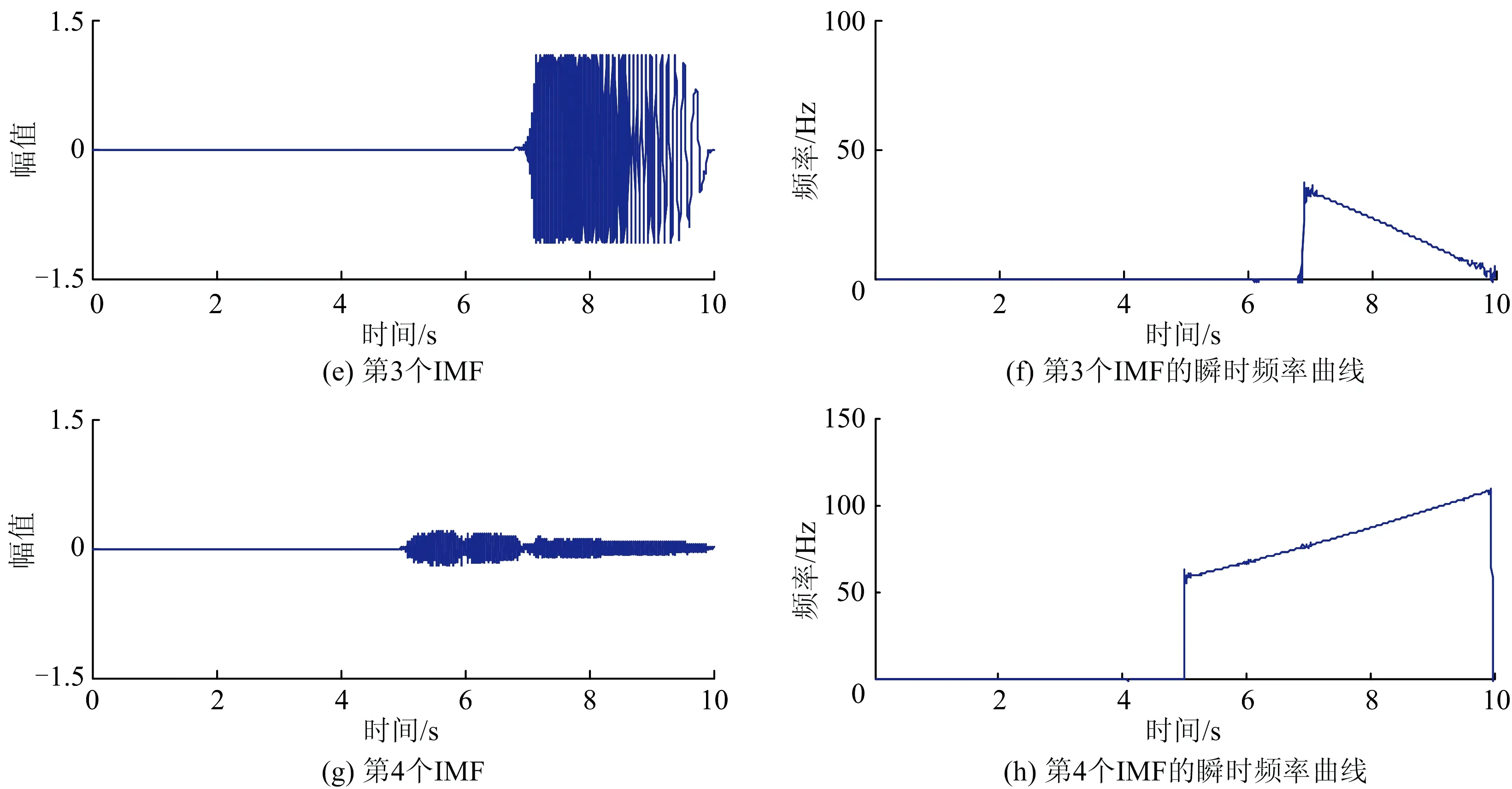
图3 采用SST方法分离出的4个IMF及对应的瞬时频率曲线

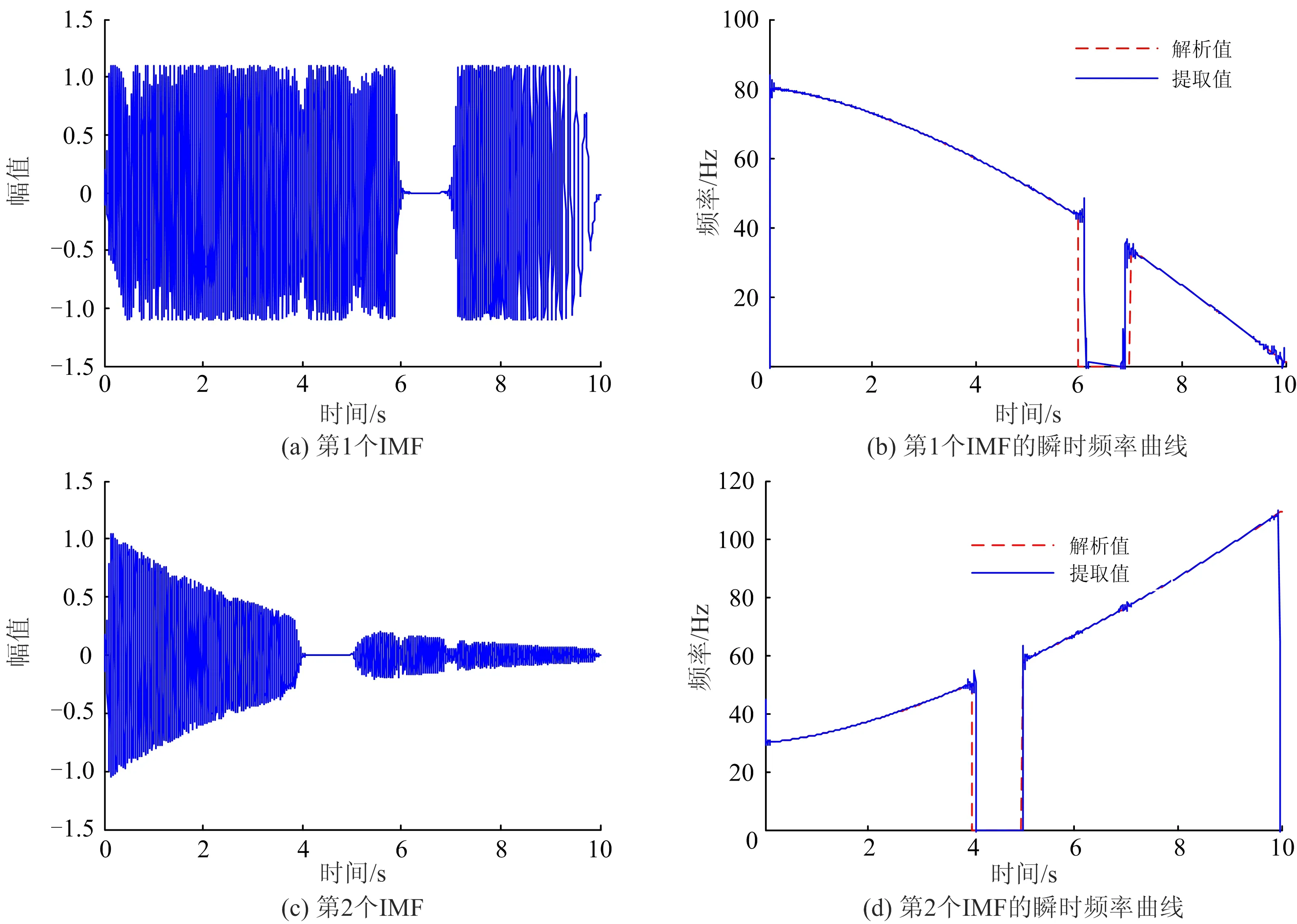
图4 采用改进方法分离出的2个IMF及对应的瞬时频率曲线

2.2 与EEMD-Hilbert变换和WVD方法的对比

为了对比验证本文方法的有效性，首先选择利用EEMD对信号进行分解，然后再利用Hilbert变换得到时频谱。在进行分解时，加噪次数为50，噪声标准差为0.1，由此得到的时频谱如图5(a)所示，可以看出，该方法所得到的时频谱时频聚集性较差；然后选择利用WVD方法得到时频谱，如图5(b)所示，从图可以看出，该方法所得到的时频谱上出现了严重的交叉项。

分别利用Hilbert变换得到的时频谱和WVD方法得到的时频谱进行频率曲线提取。由于Hilbert变换得到的时频谱时频聚集性较差，导致无法将频率曲线准确提取出来；而利用WVD得到的时频谱提取的信号的瞬时频率如图5(c)所示，可以看出，提取出的瞬时频率曲线包含了交叉项。

将图4(b)，(d)与图5(c)对比可知，采用改进方法提取出的瞬时频率曲线无交叉项，且成分较完整，说明本文提出的改进方法计算结果更好。

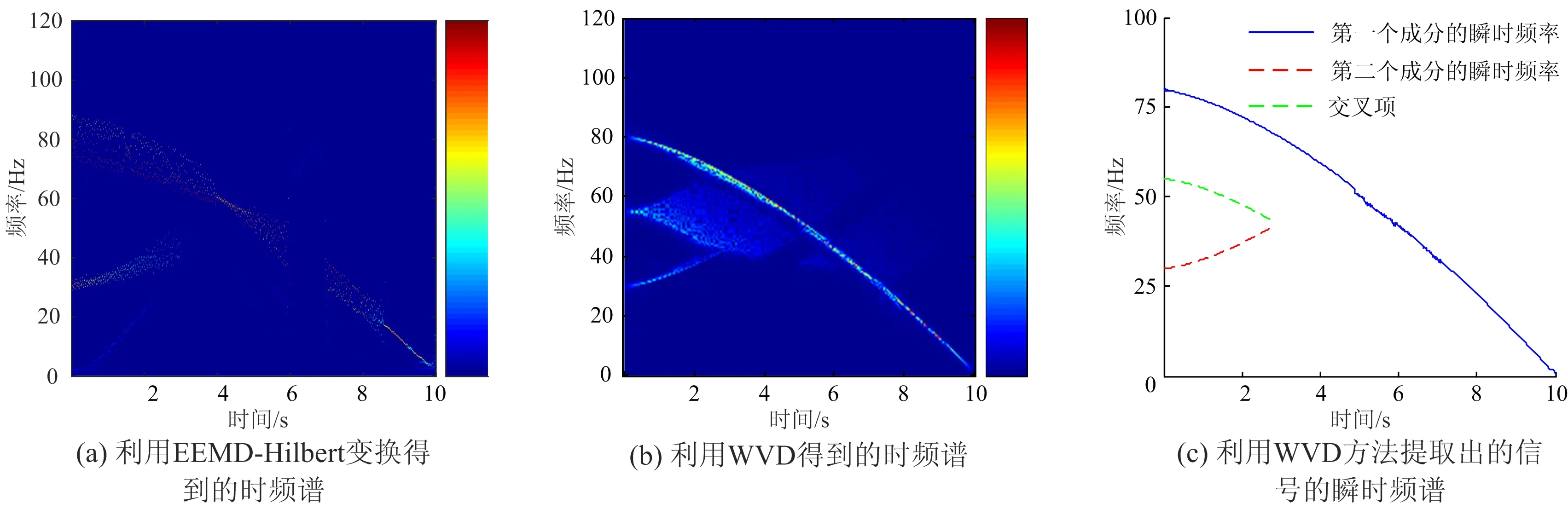
图5 信号的时频谱及瞬时频率曲线

3 高速铁路周期性轨道短波病害动态响应的时频特性

3.1 多断面加速度检测系统

在高速综合检测列车上安装的多断面加速度检测系统，可实时采集车体、构架和轴箱的加速度。检测系统采用多通道分布式网络化测试技术，用计算机远程控制分布在不同地点的测试设备同步工作，并通过网络传输数据和同步信息，具有测量数据量大、地域分散、测试的实时性和可靠性高、远距离协同操作等特点。

检测系统由轴箱加速度传感器、数据采集计算机、测量仪和展示系统组成，其中传感器安装位置如图6所示，数据采集计算机、测量仪以及展示系统安装在列车上。

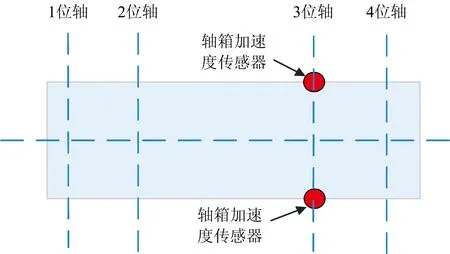
图6 传感器安装位置

3.2 打磨痕迹区段时频特性

选取如图7(a)所示的某一高铁线路存在打磨痕迹区段的轴箱加速度信号，利用SST方法对信号进行分析，得到的时频谱如图7(c)所示。由图可知：SST方法计算所得时频谱聚集性较好，并且能够与图7(b)所示信号的功率谱完全对应。

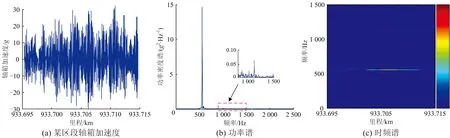
图7 某区段轴箱加速度及功率谱和时频谱

采用改进方法，在图7(c)所示的时频谱上提取轴箱加速度的瞬时频率，提取得到的频率曲线如图8所示。从图可看出：该区段轴箱加速度波形呈现周期性，其主频与图7中(b)图所示的功率谱严格对应；轴箱加速度第1主频是562 Hz，在运行速度为304 km·h-1时，对应的波长为150 mm；轴箱加速度第2主频是1 125 Hz，对应的波长为75 mm。

对该区段进行测试及复核，发现该区段的轨面存在周期性打磨痕迹，如图9(a)图所示。钢轨表面平直度测试数据和功率谱分别如图9中的图(b)和图(c)所示，可以看出，钢轨打磨痕迹波长约为75 mm。由此说明，改进方法能够有效提取出车辆动态响应信号中的特征成分。

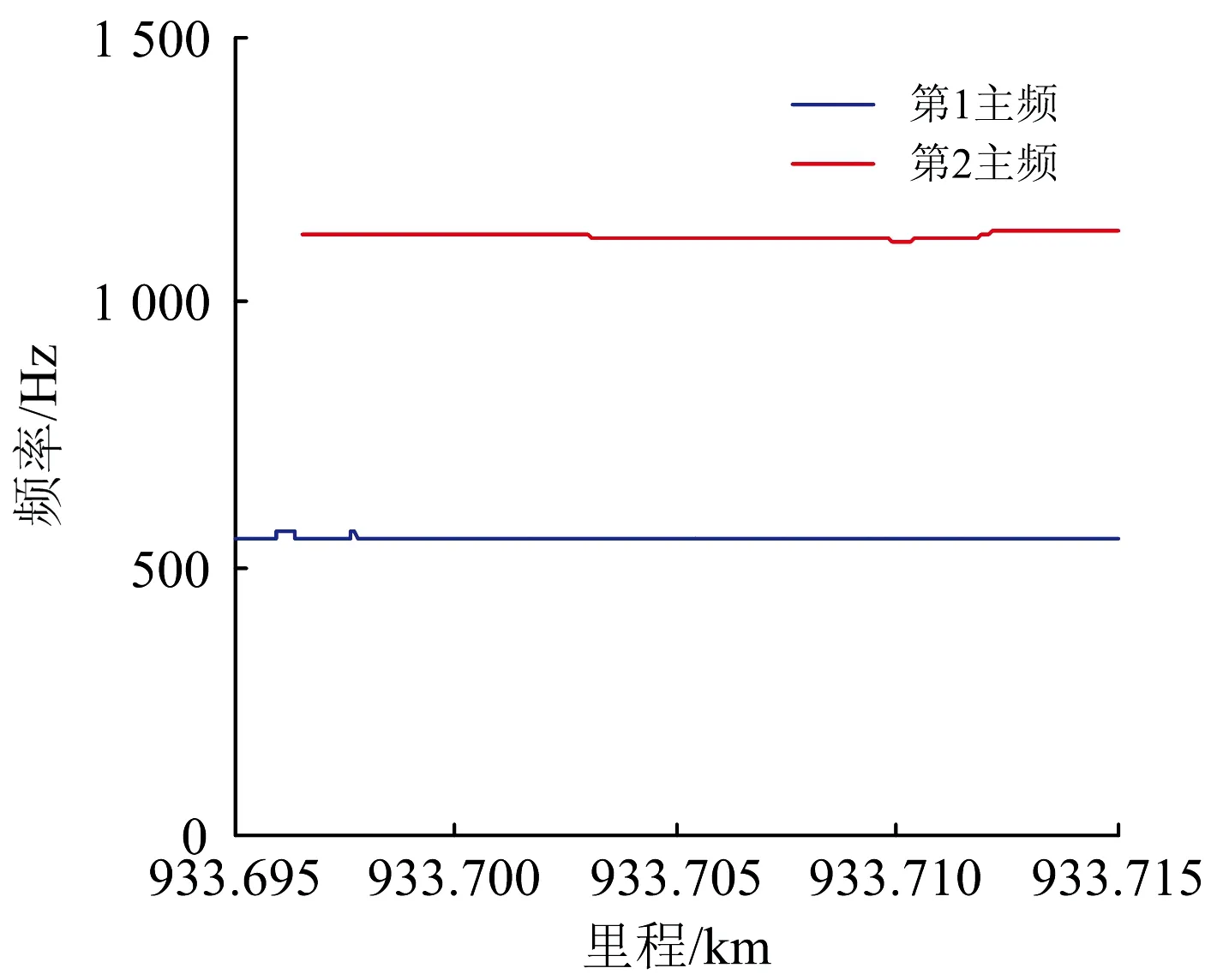
图8 某区段轴箱加速度频率曲线

3.3 钢轨波磨区段时频特性

另一区段的轴箱加速度信号如图10(a)所示，利用SST方法对该信号进行分析，得到的时频谱如图10(b)所示。采用改进方法在图10(b)所示的时频谱上提取轴箱加速度的瞬时频率，提取得到的频率曲线如图10(c)所示，可以看出，轴箱加速度波形呈现周期性，主频为562 Hz，运行速度为304 km·h-1，对应的波长为150 mm。

对该区段进行现场测试及复核，该区段的钢轨表面和平直度分别如图11(a)和(b)所示，呈现明显钢轨波磨特性。对该波磨区段轨面平直度进行分析，其空间频谱如图11(c)所示。从图11可知：该区段信号的周期性较强，波磨的波长为150 mm，与轴箱加速度分析结果一致。并且其波长恰好为打磨痕迹的2倍。

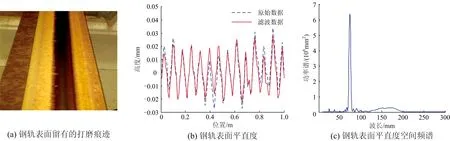
图9 留有打磨痕迹区段钢轨表面平直度及空间频谱

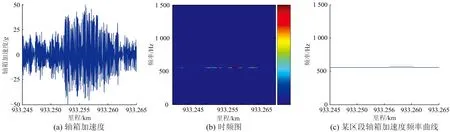
图10 某区段的轴箱加速度及时频图

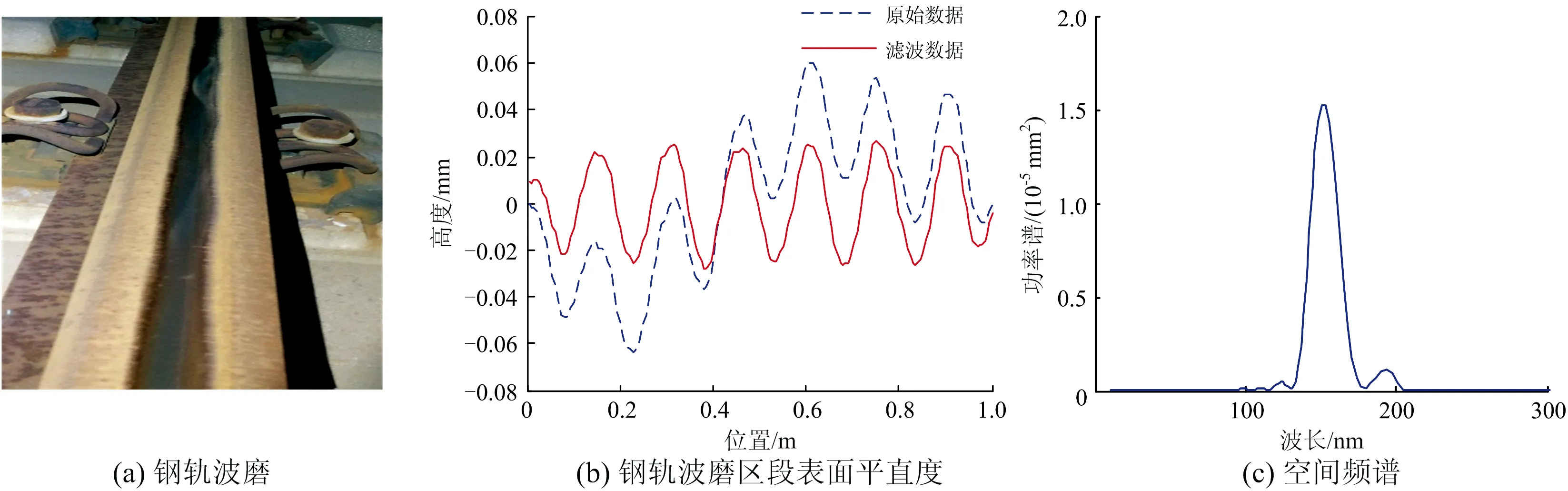
图11 钢轨波磨区段表面平直度及其空间频谱

3.4 高速铁路钢轨波磨形成机理

当某一激励作用于非线性系统时，非线性系统产生的响应有可能很微弱，但是也有可能会产生剧烈的共振现象。当系统具有N(N≥1)次方非线性时，如果系统固有频率ω0接近激励频率ω的N倍，则会产生N次超谐波共振；如果系统固有频率接近激励频率ω的1/N倍，则会产生1/N次亚谐波共振[9]。而高速铁路轮轨系统具有非线性特性，从而导致在某些工况下会产生谐波共振现象。

经过对多次检测数据的分析发现，钢轨表面打磨痕迹存在多种波长，而产生波磨区段钢轨表面波磨波长与周期性打磨痕迹波长呈现倍数关系。当打磨痕迹为75 mm时，综合检测列车以304 km·h-1的速度经过该区段，轴箱振动动态响应频率为1 125 Hz，该线路该区段所使用扣件的固有频率(不同扣件对应的施工扭矩会有差别)大约为562 Hz[10]，两者呈现倍频关系。当车辆经过此处时，钢轨表面的周期性打磨痕迹引起轨道—车辆系统的非线性振动，从而导致扣件系统产生共振，扣件共振现象又反作用于钢轨，从而导致轮轨接触表面相互作用，发生接触共振，引起钢轨表面产生塑性变形，并在下一次滚动接触时激起更大幅度的振动，形成塑流性波磨[11]。

对于钢轨周期性打磨痕迹造成的1 125 Hz的振动，只有在某一固定的列车速度时振动响应最大，所以在一定的速度范围内，钢轨周期性打磨痕迹引起的轮轨系统周期性振动频率刚好为扣件固有频率的2倍，从而导致轮轨系统产生谐波共振，导致磨波的产生及发展。但是列车在不同的区段运行速度是不同的，同时扣件扭矩的细微差别导致其固有频率有变化，所以导致在某些区段波磨较为严重，而在另一些区段波磨较轻抑或未产生。

4 结 论

(1)对基于SST变换提取瞬时频率的方法进行改进。以解析信号为例，分别采用本文改进方法、EEMD-Hilbert方法和WVD方法分析得到时频谱，并提取瞬时频率，得到频率曲线。结果对比发现：采用改进方法提取出的瞬时频率曲线无交叉项，且成分较完整。

(2)采用本文方法，分别对某高铁线路存在钢轨打磨痕迹区段、钢轨波磨区段的轴箱加速度信号进行分析，提取出钢轨短波不平顺的瞬时频率，根据瞬时频率变化特性精确定位钢轨疑似波磨和打磨痕迹区段。轴箱加速度波形均呈现周期性；在存在钢轨打磨痕迹区段，轴箱加速度第1主频是562 Hz，在运行速度为304 km·h-1时，对应的波长为150 mm；第2主频是1 125 Hz，对应的波长为75 mm；在钢轨波磨区段，主频为562 Hz，运行速度为304 km·h-1，对应的波长为150 mm；现场实测验证了该结果的正确性。轴箱加速度信号较好地反映了钢轨表面周期性病害的特性。

(3)高速综合检测列车经过钢轨波磨区段时，轮轨系统产生周期性振动，导致轴箱加速度呈现周期性振动特征，在一定的速度范围内，75 mm的钢轨周期性打磨痕迹引起轮轨系统的非线性振动，振动频率达到1 125 Hz，与扣件固有频率562 Hz呈倍频关系，导致扣件产生强烈的共振，从而引发轮—轨接触共振，导致钢轨表面产生塑性变形，形成塑流性波磨，在列车的反复作用下，导致该处产生150 mm波长的波磨。