海洋磁测中单台站地磁数据补缺方法探讨

张向宇 关永贤 王功祥

（1.国土资源部海底矿产资源重点实验室 广州海洋地质调查局，广东 广州 510075；2.南方海洋科学与工程广东省实验室（广州），广东 广州 511458）

随着国家海洋战略的实施，海洋测量工作量与日俱增，海洋磁力测量已成为我国涉海部门进行海洋探测的重要手段之一。日变改正是海洋磁测数据处理中一个重要环节，而地磁台站日变数据的质量直接影响着日变改正的效果，进而影响最终提交的磁测成果数据的精度。一般是选择工区附近的固定地磁台站或在大范围地磁普测期间在工区内投放海底地磁观测站来获取地磁日变数据，但受制于测量环境等因素的影响，经常会出现部分地磁日变数据缺失的情况，导致部分测线无法进行日变改正的情况，根据海洋调查规范[1]要求，对于无法进行日变改正的测线需作废处理，这样将导致工作量不达标，进而影响成果的提交。

目前国内外学者对于日变数据的补缺处理大多是运用多台站数据进行计算，单汝俭等[2]在1990年提出了二维多项式最小二乘拟合法、时空拟合法和线性内插法这三种局部地区地磁日变的拟合方法；边刚等[3]在2009年对加权平均法和函数拟合法进行了分析，并进行了实例验证，该方法不考虑经度效应的影响，使用纬度方向的距离来计算某点的日变改正值；卞光浪等[4]在2010年利用纬差加权法进行多站地磁日变改正值计算，将日变数据的差异只建立在纬度差关系上，通过实例进行计算验证，证实该方法较距离加权法效果更好；张向宇等[5]在2016年在纬差加权法的基础上引入回归分析法推算某处地磁日变数据，通过实例分析，验证了方法的可靠性；彭飞等[6]在2015年对调和分析法进行了分析，建立了日变数据处理谐波分析模型，将磁静和磁扰数据进行了合理分离；刘帆等[7]在2016年对谐波分析法进行了进一步研究，采用最小二乘法确定谐波系数，再取一定截断阶数的傅里叶级数作为太阳静日变化模型，以此进行磁扰数据的分离，取得了较好效果。

在实际工作中，经常会遇到获取的某一地磁台站缺失部分数据的情况，这时会考虑用上述文献中提到的多种地磁日变数据计算方法进行补缺，但这些方法均要求有合适的地磁台站数据作为样本，若待补缺地磁台站所处位置附近无可用地磁台站数据作为样本，则依然无法完成补缺工作，最终会直接影响日变改正工作的进行。因此针对单一地磁台站缺失部分数据的情况，研究相关方法进行数据补缺，尤其是在附近无可用地磁台站时进行数据补缺是十分必要的。

1 方法设计

本方法结合了信号分析中的谐波分析法和统计学中的聚类分析和相关分析法，首先使用谐波分析法对磁测数据进行频谱分离，再使用相关分析和聚类分析对静日变数据进行遴选和计算，获取静日变样本数据，最后与分离出的磁扰数据合成，进行数据重构，得到最终的结果，从而完成数据补缺，具体的流程如图1所示。

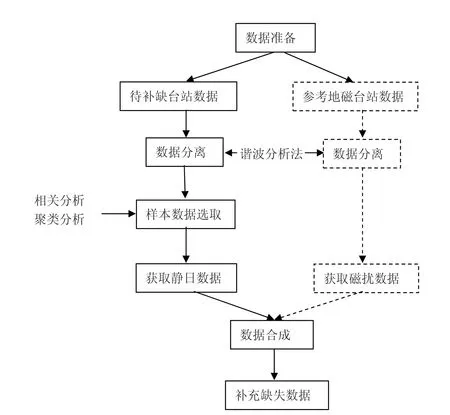
图1 单台站地磁数据补缺方法流程图

1.1 数据准备

需要准备的数据有两个，一个是待补缺台站的数据，即除了缺失数据时间段外的所有数据，此部分数据为必需数据，另一个是参考地磁台站数据，只需提供参考地磁台站在缺失数据时间段内的数据，若缺失时间段为磁静日，则该数据可不必提供，磁静日的判断需参考地磁指数，一般kp指数大于3-即为磁扰发生时。参考地磁台站需与待补缺地磁台站处于相同纬度，且经度差距越小越好，若相同纬度处无地磁台站数据可用，则以纬度最近原则，选择与待补缺台站距离最近的地磁台站为参考台站，参考台站需在缺失数据时间段内数据完备齐全。

1.2 数据分离

需要对准备好的待补缺台站数据和参考台站数据分别进行静日变化和磁扰的分离，采用的方法是谐波分析，首先对准备好的待补缺台站已有数据进行分析，选择已有数据中的磁静日数据进行数据分离，逐日分离出磁静数据备用，对参考地磁台站数据同样进行数据分离，并保留待补缺时间段内的磁扰数据。

1.3 样本数据选取

静日变化数据是以天为单位具有周期性的，可通过谐波分析法对周期性磁静日地磁变化规律进行重构，但重构时受测量噪音或低幅度磁扰的影响，会导致分离出的静日变化数据不准确，为了减小这种噪音影响，采用以多天的静日数据为样本，求取均值的方法获取最终的静日数据，可有效减小误差，这里在做样本选择时运用的方法是相关分析及聚类分析。

1.4 数据合成

对于选择好的静日变化样本数据，以天为单位对其求均值可获取最终的静日变化，因静日变化数据是以天为周期重复的，故只需将获得的磁静数据依完整的一天时间为单位进行复制即可，若待补缺时间为磁平静期，则补缺工作到此完成，若待补缺时间为磁扰期，则需将由参考地磁台站数据中分离出的磁扰数据依全球时附加到静日变化数据中，合成数据后，即可完成数据的补缺。

2 实例分析

某工区野外测量时间为2019年7月4日至27日，作业期间投放了两台海底地磁观测站，两台海底观测站投放位置纬度相同，经度相差17度，设定西侧的海底地磁观测站为1号台站，另一台为2号台站，两台站实测为F分量，数据间隔均为1 min。假定1号台站7月21日缺失地磁日变数据，则以2号台站做为参考台站，采用上述方法进行数据补缺，并将计算结果与1号台站21日的实测数据进行对比。

首先需要对1号台站数据采用谐波分析法进行数据分离，分离时取谐波次数为5，时间间隔为1 min，测量时间内kp和ap指数如图2所示。

由图2可知2019年7月至9日及7月14日至20日这9天均为磁平静日，分离后的磁静数据如图3所示。将分离出的9天的磁静数据进行相关分析，结果如表1所示。

根据相关分析的结果，选择相关性较高的9日、15日、16日、20日数据为样本，其中20日最接近21日，因此以20日的静日变数据为基准，通过聚类分析找寻与20日静日变数据最接近的数据，对上述日期分离后的静日变数据进行聚类分析，分析后的树状图如图4所示[8-10]。

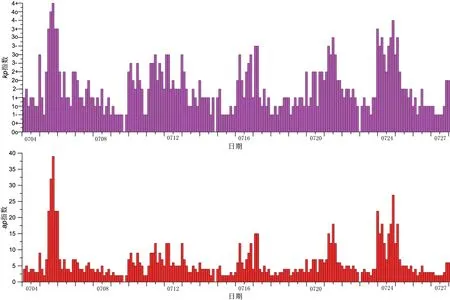
图2 测量时间内地磁指数分布图

图3 1号台站磁静数据分离结果对比图

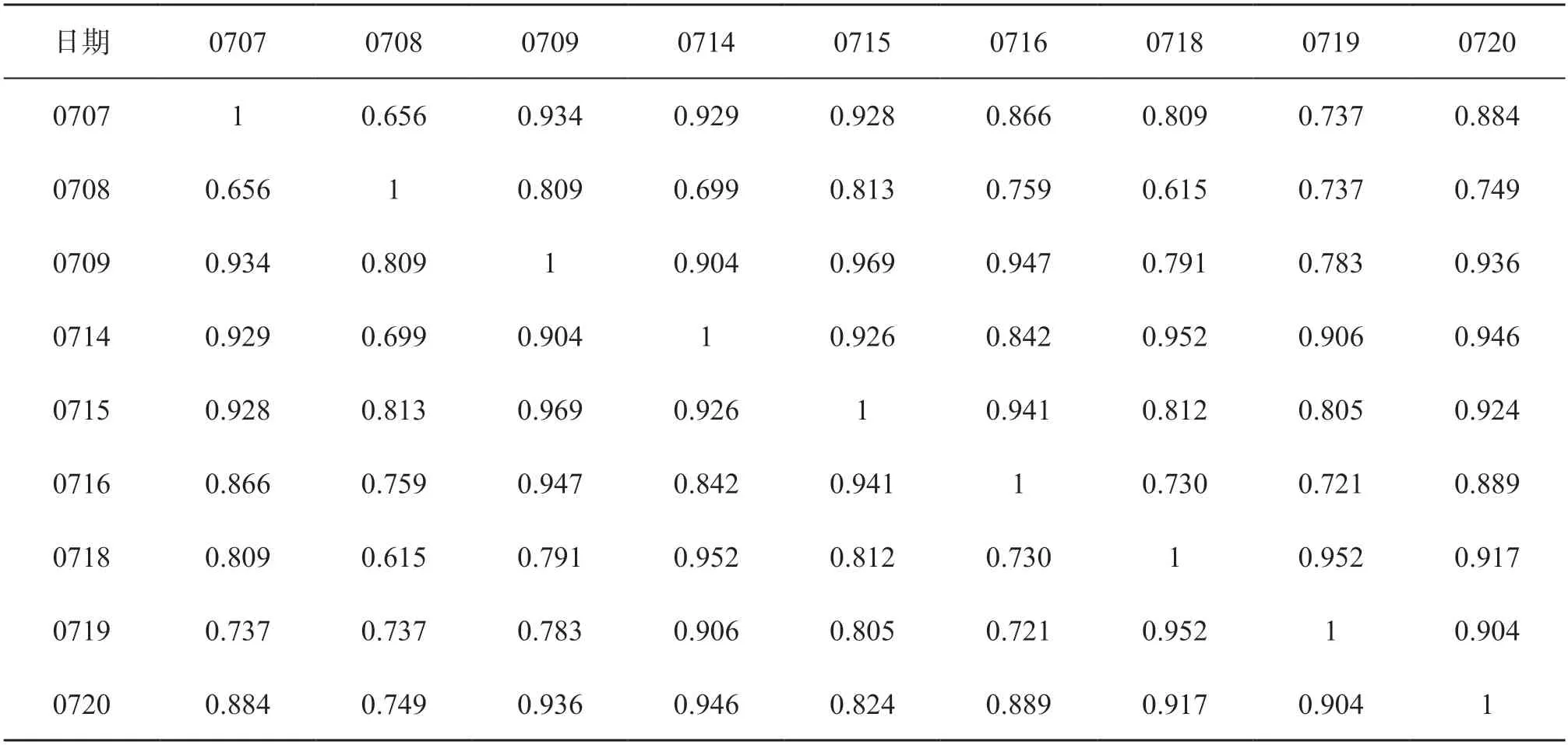
表1 磁静数据相关性分析表

图4 1号台站静日变数据聚类分析树状图

从图4中看出，与20日的静日变数据聚类最接近的是14日的静日变数据，且从表1中可以看出14日和20日的磁静数据相关性也较高，相关指数达到0.946，因此最终选择14日和20日静日变数据为最终样本，对其求取均值后，得到计算出的静日变数据，如图5所示。

图5 1号台站静日变化计算结果曲线

通过查询kp指数，7月21日的kp指数大于3-，为磁扰日，因此需要从2号地磁台21日的实际观测数据中分离出磁扰数据，在分离磁扰数据前，先选取7月24日和25日这两个磁扰日1号台站及2号台站的观测数据进行比较，结果见图6。

图6 两台站磁扰日地磁日变观测数据对比图

从图6中看出，两台站磁扰发生时间一致，无时延，磁扰发生幅度相近，量级一致，对这两组数据进行相关性分析，求得相关系数为0.938，相关性较好。由此说明2号台站作为1号台站磁扰日数据补缺的参考地磁台站是合理的。对2号台站7月21日数据进行数据分离，得到磁扰数据，结果见图7所示。

将由1号台站数据计算的静日变数据和由2号台站分离出的磁扰数据进行组合后，得到1号台站7月21日的地磁日变数据，即完成补缺工作，结果见图8。图中红色曲线为实际观测值，蓝色曲线为补缺数据。

图7 2号台站分离的磁扰曲线

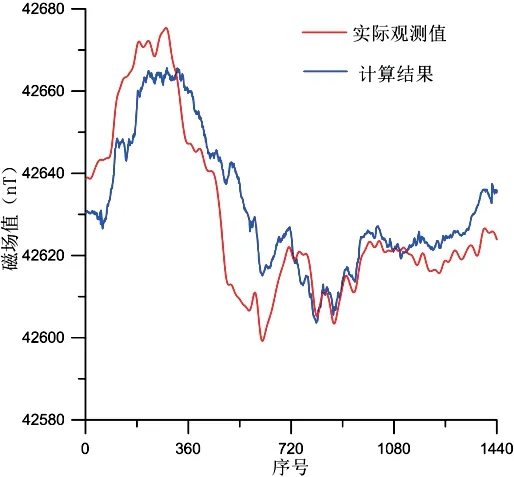
图8 1号台站7月21日数据对比图

统计计算数据和实测数据的偏差，最大值为19.2 nT，均值为8.2 nT，因7月21日是磁扰发生时段，而磁扰的发生本身对计算会带来很多影响，海洋调查规范[1]中要求磁异常ΔT精度≤5 nT，即原始磁测数据经过预处理及精细处理后得到的测网磁异常ΔT交点差中误差≤5 nT，日变改正为预处理中的一项，以上计算数据与实测数据偏差均值为8.2 nT，即日变改正误差为8.2 nT，这种程度的误差可在后续数据调差处理中进行一定程度的消除，使得最终的磁异常ΔT，值精度达标。另外从图8中看出，两条曲线形态具有一致性，但存在时延和幅值差异，这是因为静日数据是由该台站其他日期静日数据合成而来，静日数据虽是以天为单位的周期函数，但在每个周期内受地磁场变化影响，幅值相位会有所不同，尤其是每日0时至12时段内，是地磁日变化幅度较大的时段，这种偏差会更为明显，而这种因地磁场变化带来的幅值和相位的偏差也是不可避免的，在静日数据合成前采用相关分析也是为了尽量减小这种偏差。通过以上实例分析可知，采用本文方法重构的地磁日变数据与实测日变数据曲线形态一致，两组数据偏差在合理范围内，说明该方法在实测数据处理中具有一定的效果，可有效解决单台站数据缺失的问题。

3 结论

本文通过对方法及实例的分析研究，得到以下结论：（1）该方法结合了信号分析中的谐波分析法和统计学中的聚类分析法，这两种方法都是较为成熟的方法，易于实现，且可有效提升结果的准确性；（2）当待补缺时间为地磁平静时，则不需其它台站数据做参考，便可完成数据补缺；（3）该方法在使用时需要参考地磁指数来区分磁平静时和磁扰时，再依据地磁日变数据的特性，对数据进行组合，得到最终的结果。

综上，本文使用的数据补缺方法在可获取数据有限的情况下，尤其是无距离相近台站数据可用时，可有效地解决单一地磁台站数据缺失的问题。在磁平静时可只凭借台站本身已有数据便可完成数据补缺，解决了日变改正中时常遇到的问题，保证了磁测数据预处理工作的进行。