应用协方差分析方法进行数据统计分析的研究

□ 文| 李 东

选题的目的和意义

众所周知，在教育中，分数可以反映学生最近的学习情况。但是不能使用一种测试来评估学生，因此我们必须科学。合理的分析成绩来发现学生的不足，然后共同努力弥补。

T检验分析实例

1.相关样本，容量小于30的T检验。同一批学生在实验前后进行两次测试得到两次成绩，若把这两次成绩看成两个样本的话，则这两个样本之间相互不是独立的，称为相关样本。在五年级（3年级）进行了“汉语口语作文对汉语学习成绩影响的实验研究”，每节课需要10分钟，以为学生提供一次作文比赛。实验前将进行口语能力测试，并随机选择10名学生。中文学习记录（测试前结果）如表所示，一学期后，语言成绩记录所有10名学生的结果（测试后结果），并附上相同难度的测试题。结论：尽管5年级（3）的实验成绩单的平均成绩=71，5年级（3）的实验成绩单的平均成绩=79.5。1＜2，但这并不意味着实验后的5（3）级要比实验之前好，上述均值之差的测试意义具有科学依据和得出的结论。

2.不同样本，容量小于30的t检验。（1）协方差分析的提出。无论是单向分布式分析还是多因素分布式分析，人类都可以控制特定的控制变量。实际上，某些随机因素很难人为地控制。但是，这对结果有很大影响。忽略这些因素的影响可能导致错误的结论。（2）协方差分析的计算公式

在分析单向协方差的示例中，方差平方和表示：

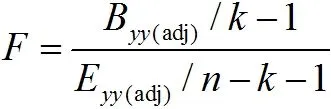
方差分析继续使用F检验和原假设，0H是不同程度的多个控制变量，总体均值之间没有显着差异。22SFS协方差协变量随机变量=

当控制变量F的共同概率小于或等于显着性水平时，并且当方差的共同概率不同时，控制变量的不同水平会对观察变量产生很大的影响。CoF低于协方差的不同显着性水平。这三种教学方法似乎在测试分数上没有显着差异。但是，如果将先前的测试分数用于协方差分析，变量影响很大。（3）协方差分析需要满足的假设条件。一是自变量是协方差变量，等距离变量和因变量是连续变量；二是测量连续变量或判断变量的协方差必须无误差；三是协变量与因变量的关系是线的。可以使用kovariate和因变量分布图用于检验该假设。（4）协方差分析SPSS的示例。在尝试新的在外语教学法中，经常在实验前后对我们测试了实验组和对照组的性能，以确定新教学方法对实验结果的影响。显然，审判前分数与审判后分数之间存在自然联系。如果您想更准确地判断新教学方法的效果，测试前分数的影响。实验后得分，这意味着您可以在测试前得分协方差的分析就是协方差。

讨论

尽管t检验是最简单的假设检验。但是，将此测试用于统计推断时，有一些注意：首先，在t检验过程中，对样本进行方差均匀性测试。其次，在假设检验描述中由于使用有争议的证明方法，因此原假设只能描述为否定或否定，其他解释是不合适的。除了本文介绍的两个样本测试之外，还有一个单一样本测试和一个对三通。单个样本的特殊性是将现有的平均值和方差用于比较。匹配的t检验是两个独立样本的t检验的另一个扩展。这个t测试是基于样本的匹配。然后将一些因素分配给两组进行t检验。

结论

在本文中，笔者将介绍t检验的基本原理，限制，应用和注意事项，并确认t检验可用于实际教育中，并且根据实验数据和实际数据具有特定的效果。因此，教育和研究可以使用统计推理技术（例如测试）来提供有关教育的科学建议。