轨检仪矢距测量系统的频响特性及其弦长选择

魏晖，邬远天，杨飞，刘敏

轨检仪矢距测量系统的频响特性及其弦长选择

魏晖1, 2，邬远天3，杨飞4，刘敏5

(1. 江西科技学院 协同创新中心，江西 南昌 330098；2.江西省铁路大数据技术开发与应用工程研究中心，江西 南昌 330098；3. 江西水利职业学院 建筑工程系，江西 南昌 330013；4. 中国铁道科学研究院 基础设施检测研究所，北京 100081；5. 中航工业上海航空测控技术研究所，上海 201601)

轨检仪矢距测量系统虽可通过“以小推大”实现长弦中点矢距的测量，但其频响特性及其优选弦长尚需明确。本文以矢距测量系统为研究对象，通过频响特性分析明确其在不同波长轨道不平顺激励下的增益及相位；在此基础上，以对高速铁路轨道敏感波长的响应最大为目标，通过整数规划选择矢距测量系统弦长倍率；并对相关观点进行仿真验证。研究结果表明：基弦的中点矢距的“以小推大”，等效于其测量弦长扩展倍，且依然保持严格线性相位；为保证有效检测敏感波长不平顺，扩展倍弦长应取70 m为宜。所得结论有利于指导高速铁路轨道的静态检测。

轨道检查仪；频率响应特性；中点弦测模型；“以小推大”算法；弦长选择

轨道检查仪(下简称轨检仪)作为重要技术装备，已广泛列装于工务各部门。轨检仪[1]通过电子、传感技术移动测量并自动记录轨道内部几何参数。铁路轨道作为大型工程结构物，其几何形位关系表征较为复杂，诸如高低、轨向(正矢)以至轨变、扭曲等项目均有着不同的测量基准且与特定的尺度相联系[2−3]。但受限于测臂尺寸，轨检仪基弦长一般≤1 m，故不能直接测量高低、轨向(正矢)等项目。为完整的获得基弦以上不同尺度的高低、轨向(正矢)等矢距参数，轨检仪的矢距测量系统采用“以小推大”的方法计算倍弦中点矢距。朱洪涛等[4]采用类渐伸线方法给出“以小推大”算法的推导，证明倍弦的中点矢距为基弦中点矢距的线性组合。此方法解决了倍弦条件下大尺度高低、轨向(正矢)等矢距参数的测量问题，然而弦测法具有选频作用[2, 5]，轨道高低、轨向不平顺“以小推大”后的响应并不清晰。这种情况下，其应用过程中有2个问题亟需明确：1)矢距测量系统通过“以小推大”算法将基弦中点矢距展成长弦中点矢距后，其输出的幅值、相位与轨道不平顺(轨道变形函数)之间的关系将如何？2)轨道几何不平顺存在特定敏感波长[2−3]，在已知矢距测量系统的幅值、相位畸变的情况下，轨检仪的倍弦长如何选择可满足高速行车的平顺性测量要求？第一个问题涉及到弦测法及其“以小推大”算法的频率响应特性问题，第二个问题则涉及到倍弦长的优选问题。

1 弦测法原理及其“以小推大”算法

1.1 弦测法原理

依据文献[1, 5−6]，轨道的轨向、高低(正矢)等均定义为一定弦长下轨道的矢距(矢度)，如轨向偏差和高低偏差定义为 10 m 弦测量的最大矢距值。弦测法(Chord-based measurement)原理如图1所示。

设中间测点里程为，对应横向或垂向变形函数(外部几何参数)为()；测弦长为，置第1测点于里程−处，则第3测点在里程−处，相应横向或垂向变形函数为(−)与(−)；同时令系不平顺波长，单位m，则定义为空间角频率，=2π/，单位rad/m；由图1，矢距

其频域响应函数[7−9]

其中：当/2时，即为偏弦测法(Asymmetrical chord offset)；而当/2时即为中点弦测法(Mid- chord offset)，其矢距()即为中点矢距

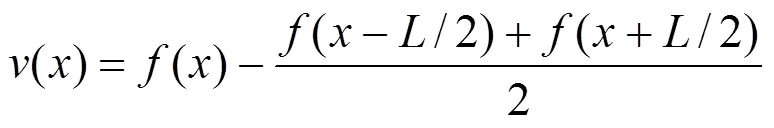
其频域响应函数[10]

图1 弦测法原理

偏弦测法与中点弦测法的幅频、相频特性如图2，易知2种方法均不满足不失真测试条件。对于偏弦测法，其对min[,−]/2以上波长谐波成分响应无过零点，可在不增加传感器前提下敏感短波不平顺[11−12]，但偏弦测法非线性相位特点使得其轨道病害现场确认困难，而其对中、长波不平顺检测也殊为不易。

中点弦测法的幅值增益由/决定并在0~2间振荡，但始终保持严格的线性相位，这一点对于轨道病害的现场确认十分有利；此外，可采用“以小推大”算法方便的检测中、长波不平顺[4]。再有，中点矢距也可直接用于指导轨道整正[13−14]，因此工务部门常采用中点弦测法评价、控制高低、轨向。

如采用等空间间隔采样方法采集轨道矢距，中点弦测法可写作差分形式如式(5)

1.2 中点矢距的“以小推大”算法

《高速铁路有砟轨道线路维修规则(试行)》和《高速铁路无砟轨道线路维修规则(试行)》[15−16]的检查项目以及高速行车条件下对不平顺敏感波长的关注均要求工务部门关注测臂尺寸以上尺度的不平顺，即需通过基弦矢距计算长弦矢距。

由文献[4, 17]，倍弦矢距的以小推大如

式中：()为里程处倍弦中点矢距。

由式(6)易知，“以小推大”算法实为一三角滤波器，其窗函数

2 轨检仪矢距测量系统的频响特性

2.1 轨检仪矢距的测量过程

轨检仪矢距的测量过程(见图3)可理解为轨道变形函数()激励矢距测量系统，经中心2阶差分以及三角滤波，得到倍弦中点矢距输出。可知，轨检仪输入输出特性取决于

式中：()，()与()分别为矢距测量系统、中点弦测法以及“以小推大”算法的系统传递函数。轨道变形函数()在矢距测量系统()作用下，其某些频率成分可能被抑制，输出产生畸变。

2.2 矢距测量系统的频响特性

采用空间域信号的等空间间隔采样方法采集轨道几何尺寸，采样步长/2；并定义空间角频率Ω=π/，单位rad。则式(4)写作

对于如式(7)所示的三角滤波器，其频域响应函数

因此，轨检仪矢距测量系统的频域响应函数

可知，经“以小推大”后，轨检仪矢距测量系统幅频特性变化规律与基弦的中点弦测法类似，增益在0~2间振荡，其群延时τ=0，具有严格线性相位。不同之处在于，经倍弦的三角滤波后，幅值增益取决于nL/λ，即频带与基弦的中点弦测法相比向0压缩了n倍。进一步由式(11)可知，对于nL为λ奇数倍情况下，G(Ω)为1；nL为λ偶数倍情况下，G(Ω)为0；2nL为λ奇数倍情况下，G(Ω)为1；其他情况下，G(Ω)为0~2。

3 倍弦长选择

依据文献[1]，轨检仪应显示并记录10 m高低、轨向与20 m正矢等项目以对标《修规》[15−16]，对其他弦长矢距并未明确要求。然而高速铁路的安全平稳还对敏感波长成分的轨道不平顺敏感。由文献[2−3]，行车速度250~350 km/h范围内时高低或方向的谐波不平顺敏感波长={10,20,60,90,100, 120}，单位m。由式(11)易知，轨检仪矢距测量系统的频域响应函数(Ω)同时受弦长倍率、基弦长以及不平顺波长3个参数的影响，无法在较宽的频带内不失真的测量各频率成分的轨道不平顺。故轨检仪矢距测量系统在前提下应尽可能响应敏感波长的轨道不平顺，或者说，通过合理设置倍弦长，使得敏感波长成分的输出足够显著并避免幅值增益为0的情况。

以为决策变量，则倍弦长选择是一类整数规划问题，其故目标函数与约束条件

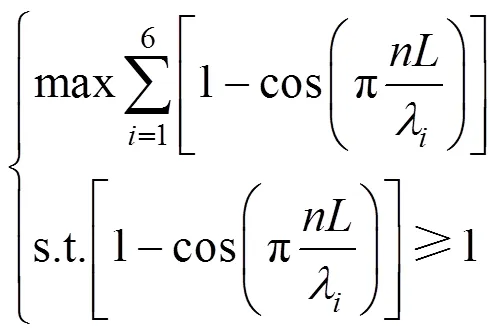
其中：={10,20,60,90,100,120}。

采用枚举法，最优解为69 m，但考虑到工务部门轨道管理习惯以及与轨检车的对标，应为10 m的整数倍，故取70 m为宜。此时敏感波长轨道不平顺激励下的幅值增益如表1所示。

表1 70 m倍弦长下敏感波长不平顺的增益

由文献[4]可知，倍弦长矢距标准差σ与基弦长矢距σ间的传递关系如

当然，与基弦相比，倍弦长矢距标准差将显著增加，如70 m弦中点矢距的测量标准差≯2 mm，则相应10 m弦中点矢距的测量标准差≯0.13 mm。

4 仿真与讨论

为验证轨检仪矢距测量系统通过“以小推大”算法对不同波长谐波不平顺的频响特性，本文采用Matlab进行了仿真。令采样间隔0.625 m，因此基弦长=1.25 m，Ω=1.25π/，倍弦长应取70 m，故=112。不平顺的变形函数除涵盖各敏感波长谐波外，另迭加了一个=/2谐波成分，故={10,20, 35, 60,90,100,120}，各谐波幅值均为1 mm。因此变形函数

将()代入式(3)计算得到的()，并()代入式(6)得到()，其波形如图4(a)；在此基础上，对()，()与()求单边幅值谱如图4(b)。

(a) 空间时域波形；(b) 单边幅值谱

图4 轨检仪矢距测量系统的输出

Fig. 4 Output of static track versine measuring system

由图4可知：

1) 空间时域波形()与()均基本保留了()波长特征且无相移；但由于/<<1，()的幅值较小，而70 m弦()与()可比；

2)()，()与()经傅立叶变换得到单边幅值谱()，()与()，可见与变形函数幅值谱()相比，()幅值增益较小，波长特征不明显；但通过“以小推大”计算倍弦后，波长特征凸显；

3) 70 m弦的()与变形函数幅值谱()相比，各敏感波长谐波幅值增益均≥1，但对=35 m成分无响应；

4) 目前较为典型的GJY-T-EBJ-3型0级轨检仪选择输出70 m高低、轨向等项目，是合理的。

5 结论

1) 中点弦测法其严格的线性相位与简便的“以小推大”算法使得其与偏弦测法相比，更宜用于轨道中长波不平顺的检测。

2) 轨道变形函数经轨检仪矢距测量系统输出基弦中点矢距与倍弦中点矢距，可在不增加轨检仪结构尺寸的条件下有效检测低频轨道不平顺 成分。

3) 倍弦长直接影响轨检仪矢距测量系统的输出，分析表明，选择70 m倍弦长有利于对敏感波长的检测。

[1] TB/T 3147—2012, 铁路轨道检查仪[S]. TB/T 3147—2012, Inspecting instrument for static geometry parameter of track[S].

[2] 罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态的控制[M]. 北京: 中国铁道出版社, 2006: 7−9. LUO Lin, ZHANG Geming, WU Wangqing, et al. Track smoothness control for wheel/track system[M]. Beijing: China Railway Press, 2006: 7−9.

[3] 高建敏, 翟婉明, 王开云. 高速行车条件下轨道几何不平顺敏感波长研究[J]. 铁道学报, 2012, 34(7): 83−88. GAO Jianmin, ZHAI Wanming, WANG Kaiyun. Study on sensitive wavelengths of track irregularities in high-speed operation[J]. Journal of the China Railway Society, 2012, 34(7): 83−88.

[4] 朱洪涛, 魏晖, 王志勇, 等. 轨检仪弦测法“以小推大”检查轨道轨向不平顺的理论研究[J]. 铁道学报, 2007, 29(1): 36−40. ZHU Hongtao, WEI Hui, WANG Zhiyong, et al. Discussion on inspection of track alignment irregularities according to method of chord measuring and its “Using small fetch big”[J]. Journal of the China Railway Society, 2007, 29(1): 36−40.

[5] 杜鹤亭. 长波长轨道不平顺检测中的数字滤波方法[J]. 中国铁道科学, 2000, 21(4): 58−65. DU Heting. Digital filtering method for long wave track irregularity inspection[J]. China Railway Science, 2000, 21(4): 58−65.

[6] TG/GW 102—2019, 普速铁路线路修理规则[S]. TG/GW 102—2019, Normal-speed railway maintenance rules[S].

[7] Insa R, Inarejos J, Salvador P, et al. On the filtering effects of the chord offset method for monitoring track geometry[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2012, 226(6): 650−654.

[8] Real J, Salvador P, Montalbán L, et al. Determination of rail vertical profile through inertial methods[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2011, 225(1): 14−23.

[9] Grassie S L. Measurement of railhead longitudinal profiles: a comparison of different techniques[J]. Wear, 1996, 191(1/2): 245−251.

[10] Ahmadian M. Filtering effects of mid-cord offset measurements on track geometry data[C]//Proceedings of the 1999 ASME/IEEE Joint Railroad Conference (Cat. No.99CH36340), Dallas, TX, USA. New York, USA: IEEE, 1999: 157−161.

[11] 魏珲, 刘宏立, 马子骥, 等. 基于组合弦测的钢轨波磨广域测量方法[J]. 西北大学学报(自然科学版), 2018, 48(2): 199−208. WEI Hui, LIU Hongli, MA Ziji, et al. A wide-area measurement method of rail corrugation based on the combination-chord system[J]. Journal of Northwest University (Natural Science Edition), 2018, 48(2): 199− 208.

[12] 程樱, 许玉德, 周宇, 等. 三点偏弦法复原轨面不平顺波形的理论及研究[J]. 华东交通大学学报, 2011, 28(1): 42−46. CHENG Ying, XU Yude, ZHOU Yu, et al. Theory and research of asymmetrical chord offset method of restoring a waveform of track irregularity[J]. Journal of East China Jiaotong University, 2011, 28(1): 42−46.

[13] 魏晖, 朱洪涛, 赵国堂, 等. 基于中点弦测模型的无砟轨道精调量迭代求解[J]. 西南交通大学学报, 2015, 50(1): 131−136. WEI Hui, ZHU Hongtao, ZHAO Guotang, et al. Iterative algorithm of HSR ballastless track realignment calculation based on MCO model[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 131−136.

[14] 郝瀛. 铁道工程[M]. 北京: 中国铁道出版社, 2000: 152−168. HAO Ying. Railway Engineering[M]. Beijing: China Railway Press, 2000: 152−168.

[15] TG/GW 116−2013, 高速铁路有砟轨道线路维修规则(试行)[S]. TG/GW 116−2013, High speed railway maintenance rules for ballast track (for trial implementation)[S].

[16] TG/GW 115−2012, 高速铁路无砟轨道线路维修规则(试行)[S]. TG/GW 115−2012, High speed railway maintenance rules for ballastless track (for trial implementation)[S].

[17] 魏晖, 朱洪涛, 刘荣平, 等. 无砟轨道轨向动静态轨向数据的差异性的时频域解释[J]. 科学技术与工程, 2013, 13(17): 5040−5045. WEI Hui, ZHU Hongtao, LIU Rongping, et al. New insights into the alignment data bias between kinematical measurement and static measurement for ballastless track[J]. Science Technology and Engineering, 2013, 13(17): 5040−5045.

Frequency response characteristics of static track versine measuring system and its priority chord length

WEI Hui1, 2, WU Yuantian3, YANG Fei4, LIU Min5

(1. Collaborative Innovation Center, Jiangxi University of Technology, Nanchang 330098, China; 2. Big Data Technology Development and Application Engineering Research Center of Jiangxi Province, Nanchang 330098, China;3. Department of Architectural Engineering, Jiangxi Water Resources Institute, Nanchang 330013, China;4. Infrastructure Inspection Research Institute, China Academy of Railway Sciences, Beijing 100081, China;5. Shanghai Aero Measurement & Control Technology Research Institute, AVIC, Shanghai 201601, China)

By employing multiple chord algorithm, static track versine measuring system of track inspecting instrument was able to measure long chord versine, but both its frequency response characteristics and priority chord length were still ambiguous. By taking static track versine measuring system as the research object, this paper analyzed its magnitude frequency and phase frequency characteristic in different wave-length irregularity inputs. On this basis, this paper established an integer programming model of chord length that was aimed at the maximum of HSR sensitive wavelength irregularities response. Finally, simulations were conducted to verify related viewpoints. It is concluded that-multiple chord algorithm of mid-chord offset is equivalent to extend the measuring chord length into-times as wide as basic chord, meanwhile maintaining the strict linear phase. To guarantee its effectiveness in measuring HSR sensitive wavelength irregularities, priority chord length should be 70 m. The aforementioned results could promote track static inspection for HSR.

inspecting instrument for railway track; frequency response characteristics; mid-chord offset; multiple chord algorithm;priority chord length

U216.3

A

1672 − 7029(2020)02 − 0335 − 06

10.19713/j.cnki.43−1423/u.T20190510

2019−06−09

国家自然科学基金资助项目(51468042)；江西省重点研发计划项目(20161BBE50079)；江西省教育厅科学技术研究项目(GJJ151157)；南昌市指导性科技计划项目(2017-KJZCCXY-014)；江西省汽车服务工程及产业升级协同创新中心开放基金(19XTKFYB02)

魏晖(1975−)，男，江西赣州人，教授，博士，从事轨道检测理论与技术研究；E−mail：weihui@163.com

(编辑 涂鹏)