“数形结合”思想下的小学数学教学分析

江西省峡江县第二实验小学 袁 琼

小学阶段学生的心智发展比较不足，思维能力的发展也不够完善，他们常常对数学有莫名的抵触，不愿学习数学，害怕做数学题，长此以往，他们学习数学的能力将大大降低。因此，小学教师需要把握小学生的心理特点，利用“数形结合”让小学生对难懂的知识点进行梳理，形象地感受数学概念，从而了解其本质。通过这样的方式，教师才能很好地完成教学目标，学生也能快速直观地理解和应用数学知识。

一、数形结合，加强小学数学概念算理掌握

在小学生学习数学的过程中，由于小学生的理解能力不足，且数学这门学科的数学思维较复杂，单单只靠文字和数字是理解不了数学概念和解决数学题的，所以教师在讲解知识点的时候，常常会用到“数形结合”方法，将晦涩难懂的文字转化为图形，将错综复杂的数字关系转化为图形，从而有利于小学生直观地理解数学知识的概念以及题目的算法。

例1：现有18 个正方体（如图1），问：

（1）每几个一堆，共摆了几堆？18÷□=□(堆);

（2）共摆成几堆，平均每堆几个？18÷□=□（个）。

在这道题中，小学生可以观察图形得到答案，即每6 个一堆，共摆了3 堆，得到18÷6=3（堆）；共摆了3 堆，平均每堆6 个，得到18÷3=6（个）。通过这种方式，在得出答案的同时，小学生也可以直观地理解除法的概念，即已知两个因数的积与其中一个因数，求另一个因数的运算。通过“数形结合”，小学生就可以加强对数学概念及算理的掌握。

例2：观察图2。

（1）在第一行中，5-□=□；

（2）在第二行中，5-□=□。

在本题中，主要考查整数的加减运算，根据图形数量可得：在第一行中，5-1=4；在第二行中，5-2=3。这种程度的加减算法相对来说是简单的，但对于数学基础差的小学生，这种数学运算与图形结合的方式既提高了他们的兴趣，又帮助他们学习了加减运算。

二、数形结合，深化小学数学教材内容挖掘

小学生正处于需要引导的时期，各方面素质能力都需要培养。因此，小学数学教师在设计教学方案时，一定要仔细研读课本内容，深度研究每个细节，争取让小学生在课堂上真正学习到数学知识。运用“数形结合”的方法，认真研究用到这种方法的相关内容，让小学生更加透彻地理解所学知识的概念。

例3：一人家里种青稞，去年共收1500 千克，今年比去年多收三成，今年共收多少青稞？

在这个例题中，为了解题方便，我们要学会怎样将已知文字条件转化为图形。首先应该画出已知条件（如图3），再分析哪年收的青稞多，即“30%”是“谁的30%”，最后分析过程结束，我们可得今年收到的青稞为1500+1500×30%=1950（千克）。

例4：现有甲、乙、丙、丁四个数，已知甲数比乙数大7，甲数比丙数、乙数比丁数都大5，甲、乙两数的积比丙、丁两数的积大140，先求甲、乙两数的积。

这道题的关系比较复杂，很多小学生一看可能会觉得头疼，对大多数小学生来说，单纯地看看是解决不了问题的，这时候就要借助图形来分析它们之间的关系。如图4，将甲、乙分别当作长方形的长和宽，则长方形的面积即为甲、乙两者之积，同样，阴影部分面积即为丙、丁两者之积，再根据题干所给信息，可得140-5×5=115，而5×（丙+丁）=115，所以可得丙+丁=23，又因甲比乙大7，所以丙-丁=7，根据两个有关丙、丁的式子，可得丙为15，丁为7。计算出这两个数，再根据所给条件，就可以很快计算出甲、乙两数的积为245。这样通过与图形结合的方式，就开辟了一条捷径，解决了一道难题。

三、数形结合，凸显小学数学隐形逻辑关系

数学是一门比较抽象的学科，无论是数学概念还是数学算法，对小学生来讲都是比较抽象的。在小学数学学习过程中，小学生要学习许多的算法，比如整数的加减乘除、小数及分数的算法，还有各种运算规律，而且还要熟练运用是很不容易的。因此，小学教师在教学过程中往往会借助“数形结合”的方式，在讲课的时候利用图形，使课堂变得生动活泼，讲授的内容也更通俗易懂。利用数形结合，将抽象的数学规律直观化，将隐性的逻辑关系明显化，便于小学生理解和吸收。

例5：现有一只“小猫”（如图5）是用七巧板拼成的，现已知它尾巴的面积是8平方厘米，求这只“小猫”的面积。

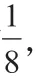
综上所述，“数形结合”的思想在小学数学教学过程中发挥着重要的作用，对老师的教学工作有很大的帮助。在新课标的要求下，新型数学课堂改变了传统课堂的沉闷无趣，更加形象生动。“数形结合”思想可以应用于小学教学的各个阶段，对于小学各个年级的学生都适用。因此，教师应设计合理的教学方案，通过数形结合，让抽象的数学概念明朗化，从而提高小学生学习数学的兴趣。