巧用圆锥曲线定义妙解高中数学竞赛题

江苏省扬州市扬州大学附属中学 张卫兵

圆锥曲线是典型的解析几何，是高中数学的重点和难点，主要包括椭圆、双曲线、抛物线等内容。在初中一元二次函数的学习中，了解了抛物线最值、顶点、开口方向、单调性等知识，但是进入高中，又新增了椭圆和双曲线知识，在原有的基础上拓展了几何图形以及直线与圆锥曲线综合问题，进一步渗透了“数形结合”思想，强调了数学模型的重要性。了解圆锥曲线定义能够在数学竞赛中快速抓住问题本质，运用数学思想和解题技巧避繁就简式解题，邂逅数与形的魅力。

一、数学竞赛中圆锥曲线知识的考查分析

本文以2000 年到2017 年全国高中数学联赛中的“圆锥曲线”试题为研究对象，进行分析、整理、归纳和总结。“圆锥曲线”是每一年数学竞赛的重点考查内容，所占分值基本在30 分左右，出题频率高且稳定，题型选择也多种多样，一般包括选择题、填空题和解答题，知识考查包括基础知识；其与数列、不等式、平面向量、函数等知识的结合：数形结合、转化与化归等思想。

二、圆锥曲线学习的重要性

解析几何是数学发展的标志性成果，圆锥曲线作为解析几何的重要组成部分，体现了解析几何的基本思想和能力。此外，它还是代数与几何的桥梁，用以培养学生利用代数方法解决几何问题的能力。圆锥曲线在高中数学教材中的所占比例较大，知识重点一直比较多。当然，解析几何又是微积分的基础，与高等数学密切相关，由此可见，圆锥曲线不仅是高中教学的关键内容，还是整个数学知识的关键组成部分，是培养学生数形结合思想、逻辑思维能力、数据分析能力、空间形象能力的重要途径。

从高中教材分析来看，圆锥曲线这部分知识对文科、理科的要求不同，安排课时不同，理科生研究更为深入，难度比较大，重点考查综合能力，会涉及向量、不等式、函数等，不仅要掌握定义、性质，还要具有很强的综合性和转化、化归能力、分析能力和计算能力，自身的知识广度与深度要达到一个新的层次；文科生研究比较基础，只需要掌握简单的应用，考查基础运用能力。

三、巧用椭圆定义妙解数学竞赛题

1.椭圆定义

平面内与两定点F1、F2的距离的和等于常数2a（2a＞|F1F2|＞0）的点的轨迹叫作椭圆。两个定点（F1、F2）叫作椭圆的两个焦点，两个焦点的距离叫作椭圆的焦距。其数学表达式为：|PF1|+|PF2|=2a。

一动点到定点的距离和它到一条定直线的距离的比为常数e（0＜e＜1），那么该动点的轨迹叫作椭圆，其中，定直线为准线，定点为焦点。该定义被称为椭圆的第二定义。

2.解题范例

剖析：此题首先梳理出题中已知条件和椭圆性质之间的关系，然后再借助定义“椭圆上任意一点与两定点之间的距离为2a（其中a为椭圆的半长轴长）”，最终求得椭圆离心率e。

四、巧用双曲线定义妙解数学竞赛题

1.双曲线定义

2.解题范例

解题思路：首先根据正弦定理得到焦半径|PF1|和|PF2|，然后再结合双曲线定义，求得离心率。

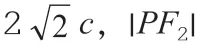
五、巧用抛物线定义妙解数学竞赛题

1.抛物线定义

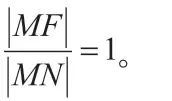
2.解题范例

解题思路：首先巧用抛物线上的点到焦点的距离与其到准线的距离进行互化，然后将其贯穿整个解题过程，最后再根据余弦定理结合不等式，求解出最大值。

由以上叙述可知，圆锥曲线知识涉猎广泛，在用定义求解相关问题时，一般会涉及焦点和准线，习惯从曲线上的点与焦点构成的三角形入手，再利用勾股定理或正余弦定理进行求解。整个过程运用到了数形结合思想、划归思想等，不仅能够培养学生的数学学习思维，还可以提升数学学习能力，找到最优解题途径，优化数学学习过程。因此，在教学实践中，教师要注重对学生进行圆锥曲线模块知识的训练，让其感受数与形的美，提升数学综合素养。