不确定环境下考虑政府补贴的双回收渠道绿色闭环供应链研究
郭健全,王振
(上海理工大学 管理学院,上海 200093)
一、引 言
自然资源短缺和生态环境恶化使得可持续发展的观念日渐被认可。再制造作为解决资源和能源短缺的一种方法,由于其具有增值潜力和环境友好的特点,越来越受到关注[1]。再制造对原材料的依赖程度较低,与制造业相比利润可能更高。对于企业而言,实施再制造已然成为企业的一项可持续发展战略[2]。然而,再制造过程却面临许多挑战。例如,需求与回收质量的不确定,企业如何选择废旧产品的回收渠道,如何建立绿色供应链,政府又该怎样引导企业回收等,这使得再制造过程的困难度增大[3-4]。
再制造过程会出现许多不确定性的问题[5-6]。Teunterrh[7]考虑到了再制造成本与需求量之间的关系,分别研究了在确定和不确定需求下的最优再制造策略。Li等[8]假设需求随机模糊情况下,建立了先定价后再制造的总成本模型。Arasn[9]通过建立数学模型来描述不同质量水平的废旧品。Galbreth[10]假设每一个废旧品的质量水平是随机的,并服从均匀分布。上述文献对需求不确定性以及回收质量水平不确定进行了单独讨论,但在供应链的运作中经常同时出现需求和回收质量水平不确定的情况,基于此,笔者拟将两者联合起来研究。
处理再制造供应链中不确定问题的方法有很多,模糊机会约束规划法便是其一[11]。Liao等[12]对市场需求进行了随机分析,并运用模糊规划法解决市场不确定问题。Marti[13]分析了整个再制造过程中的碳足迹,建立不确定市场需求下的闭环供应链模型,并用模糊规划法解决不确定问题。Wang等[14]通过对市场需求的随机分析,并运用模糊规划法研究再制造最佳回收量。Liao等[15]通过考虑回收质量的不确定性,对再制造系统进行优化。上述文献大多是用模糊机会约束法解决单个不确定性问题,笔者拟通过对比分析,采用模糊机会约束法解决市场需求和回收产品质量的双重不确定问题。
关于企业回收渠道的选择问题,Savaskan[16]为零售商设计了一个回收渠道,这个回收渠道是零售商回收的唯一途径。Feng等[17]分别探讨了单一传统回收渠道、单一在线回收渠道下的制造商利润。Chu等[18]研究了制造商回收渠道的结构问题,并分析了消费者意愿对回收渠道选择的影响。以上文献只考虑了单一回收渠道,而回收过程中企业的回收渠道往往不止一种,因此,笔者拟采用双回收渠道进行研究。
近年来,国内外学者对消费者绿色偏好行为等问题进行了较为广泛的研究。Diabat等[19]将绿色环保思维纳入供应链。Ghosh等[20]研究了产品绿色度是怎样受到渠道结构影响的。Yang[21]研究了回收不确定性下的供应链绿色决策问题。Tseng等[22]对绿色创新实践进行评估,重点关注不确定性下的创新问题。上述研究大多只涉及绿色偏好行为的研究,而笔者拟将绿色度作为参数,具体研究绿色度水平与总成本之间的关系。
针对政府该如何补贴回收与再制造活动问题,Sheu[23]研究了政府补贴对制造商回收产生的影响。Sheu等[24]研究认为,政府补贴会对第三方回收产生影响。Atasu等[25]研究了环境立法和政府补贴对回收废旧电子产品的影响。Droste[26]通过鼓励绿色投资,研究了政府补贴对绿色效率的影响。Fan[27]研究了考虑绿色偏好和补贴对家电回收的影响。以上研究仅以企业只有一个回收渠道为前提,考虑政府补贴与绿色度对企业的影响,没有给出具体可行的补贴措施,也忽略了企业可以有多个回收渠道。因此,笔者拟研究不同回收渠道和绿色度水平下的政府补贴问题。
笔者拟建立不确定环境下考虑政府补贴的双回收渠道绿色闭环供应链的总成本模型。为求解该模型,运用模糊机会约束规划方法解决需求量和回收品质量不确定问题,并采用粒子群优化算法和遗传算法对模型进行对比求解。本研究可为企业在不确定环境下制定最优策略、规划企业制造/再制造活动提供借鉴,也可为政府可量化地制定和实施补贴和再补贴提供技术和理论支持。
二、模型构建
(一)模型假设
假设:
(1)废旧回收产品全都用于再制造活动[28-30];
(2)消费者对产品的绿色偏好ϑ服从均匀分布;
(3)产品绿色度(ω)与质量(q)成正比关系,即g=wq[31];
(4)不确定市场需求量和回收质量水平。
(二)函数构建
1.再制造函数
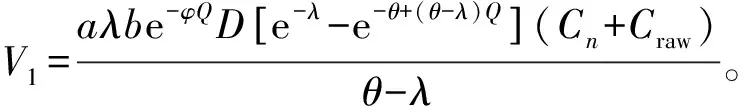
2.补贴函数
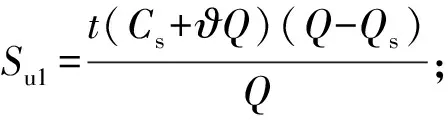
3.研发成本函数
市场上,有些消费者只愿意购买普通产品,不愿意花高价购买高绿色度产品;有些消费者则愿意支付较高的价格购买高绿色度环保产品。为了提高产品的绿色度水平,制造商需要投入资金进行新产品研发。根据Oreski等[35]的研究,假设研发投资与其结果呈二次关系,即绿色产品研发成本V8=β(g-gb)2。其中,β为绿色投资参数,gb为标准回收产品绿色度,g为产品绿色度。
(三)系统模型
制造商和第三方回收商将回收的废旧产品用于再制造。政府对第三方回收商、制造商和绿色原材料进行补贴。第三方回收商回收的废旧产品全部送往制造商。制造商购买绿色原材料和回收废旧品进行制造再制造活动,然后将产品卖到市场,最后再将市场上产生的废旧产品进行回收,从而进行循环。模型中物料流动方式如图1所示。
1.库存状况
设模型先进行再制造,然后考虑制造。其中一个周期(T)中包含m个再制造期(Tm)和n个制造期(Tn),即nDTn=DT-dT,mDTm=dT。库存状况如图2所示,再制造率为D(1/γ),制造率为D(1/β)。再制造品库存上升速度为D(1/γ-1),回收品库存下降速度为D(α-1/γ)。制造品库存上升速度为αD,原材料库存下降速度为D(1/β)。
2.平均总成本
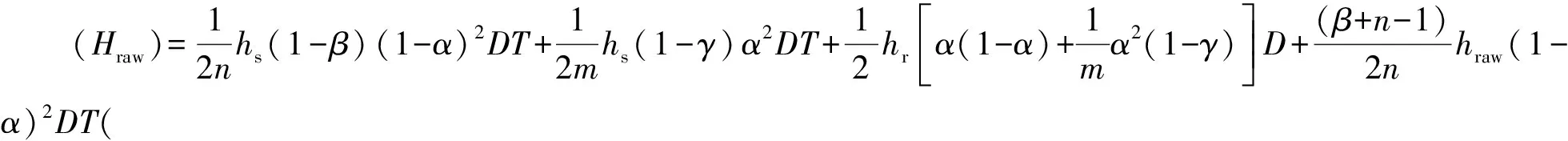
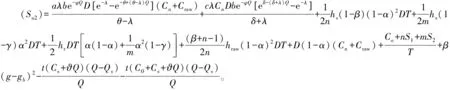
3.模糊机会约束清晰化
采用模糊规划法解决模型不确定问题[36]。需求模糊数(Di)=(Di1,Di2,Di3)以及回收质量模糊数(Qi)=(Qi1,Qi2,Qi3),其隶属函数如下:
由模糊规划法的定义[37-38]求出:
当Pos{Xdi=Di}≥αd当Pos{Xid=Qi}≥αq
三、算例分析
遗传算法和粒子群优化算法各有优势,但单一迭代过程都存在不足。遗传算法迭代过程中可能错过局部最优解,粒子群优化算法易发生早熟收敛。基于此,笔者将两种算法对比使用,以进一步验证模型的可信度。
(一)粒子群优化算法
粒子群优化(Particle Swarm Optimization,PSO)是一种受自然启发的方法,它模拟了为寻找食物而合作的一群个体之间的社会互动[39-40]。在粒子群优化算法中,种群被称为群,个体被称为粒子。在搜索空间之中,每一个粒子都以一定的速度在移动。在每次迭代中,粒子都会使用内存来保存其最佳位置和总体最佳粒子位置。经典算法将粒子分散在可行域中,然后在搜索空间中迭代移动粒子,每一个粒子在每一时刻由一个位置一个速度和它所访问过的关于适应度函数的最佳位置组成。编写步骤如下:
(1)设定粒子群规模为N,随机初始化粒子位置及速度信息。
(2)根据适应度函数获得所有粒子的适应度值大小。
(3)比较历史适应度值。
(4)根据以下算式对粒子的速度和位置进行更新:vis(t+1)=wvis(t)+c1r1[pis(t)-xis(t)]+c2r2[pgs(t)-xgs(t)]xis(t+1)=xis(t)+vis(t+1)。其中,惯性权重w取0.729 8,学习因子c1=2,c2=2,r1和r2为服从[0,1]上均匀分布的相互独立的伪随机数。
(5)如果达到设定的最大迭代次数30,则输出解;否则,返回步骤(2)。
(二)遗传算法
遗传算法(Genetic Algorithm,GA)是一种基于自然进化的迭代随机优化方法[40]。遗传算法利用生物隐喻在类染色体数据结构上编码一个潜在的解决方案,根据适应度函数定义对每个个体进行评估。在每次迭代(生成)中,选择代表目标问题的较好解的个体(父代)进行复制。新解(子解)是通过重组双亲(交叉)或随机修改一个解(变异)而产生的。这些新的候选者取代了较弱的解(个体),种群逐渐进化为适应优化问题的更好的解。编写步骤如下:
(1)编码与初始解生成,随机生成第一代种群,染色体编码用来代表个体,初始种群如图3所示。
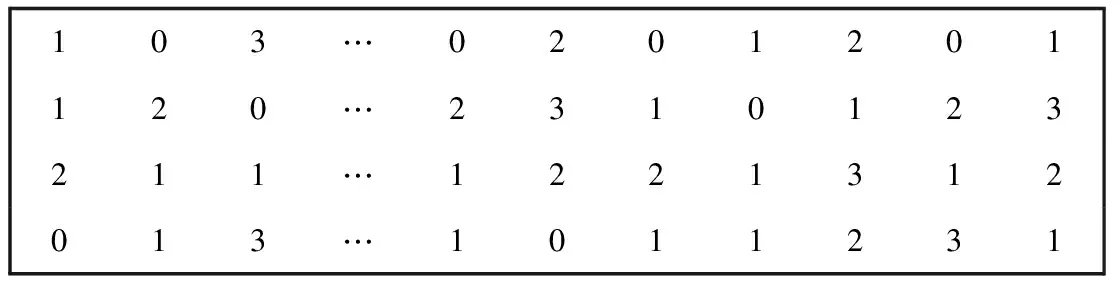
103…0201201120…2310123211…1221312013…1011231
图3 遗传算法的初始种群
(2)计算粒子适应度值。根据适应度值越高、染色体越容易被选上的原则,通过适应度函数:f(x)=1 000/objvalue(其中,objvalue为目标函数值),选择合适的粒子适应度值。
(3)交叉和变异。交叉:采用多点式交叉,随机产生交叉位,依据交叉概率判断交叉与否(如图2所示)。变异:依据已确定的变异概率,随机地选择位置变异。
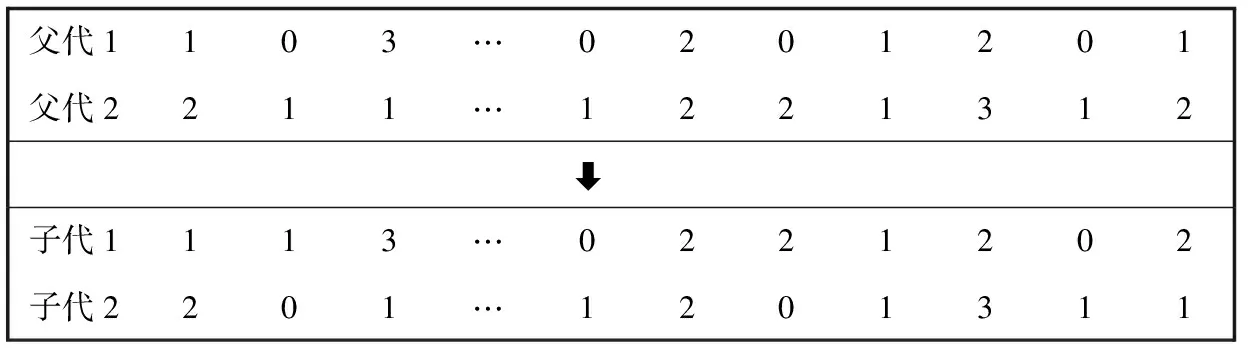
父代1103…0201201父代2211…1221312子代1113…0221202子代2201…1201311
图4 遗传算法的交叉过程
(4)终止规则,算法达到预先设置的数值时终止;否则,转入步骤(2)。
(三)计算结果
本文采用由明尼苏达大学研究院小组收集的movielens-20m数据集进行模拟运算,给出需求和回收质量三角模糊数(如表1所示)。
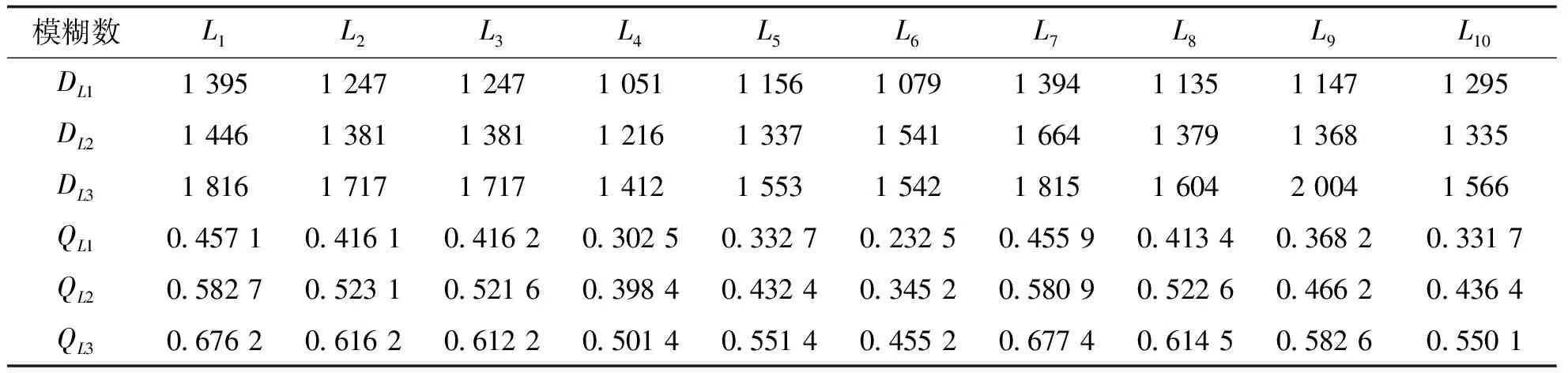
表1 市场需求和回收质量水平三角模糊数
表1所示为制造商与回收商的需求量与回收质量的三角模糊数。由表1可知,三角模糊数受置信水平的影响,因此,采取均匀分布设计法以5%极差对αd和αq分别赋值80%、85%和90%。然后将置信水平交叉而产生的9种情况代入模型中,并运用MATLAB软件编写遗传算法和粒子群优化算法代码进行求解,计算结果如表2所示。
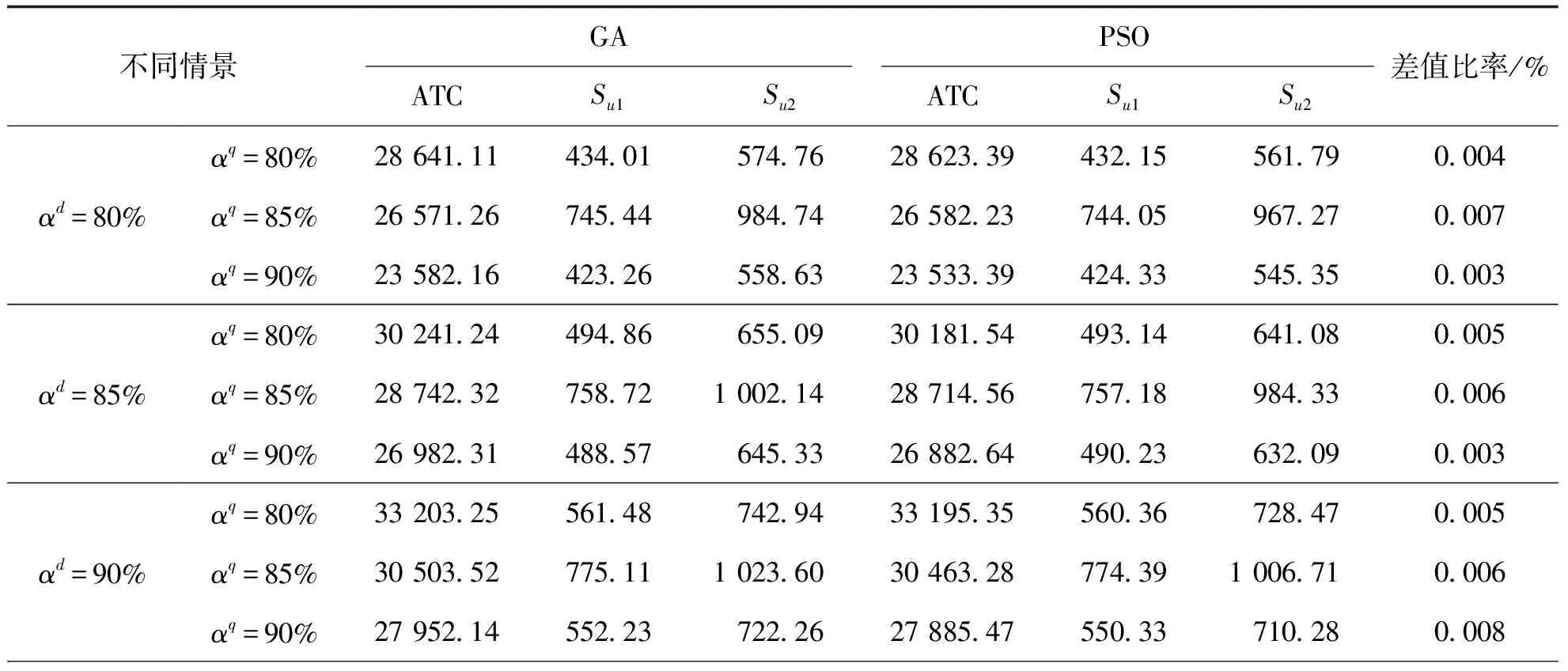
表2 不同置信水平的目标值
在预设最大迭代次数150代情况下,遗传算法和粒子群算法分别在第132代和第127代获得最优适应度曲线。当对αd,αq赋值80%和90%,即当市场需求量为1 157,回收质量水平为0.38时,平均总成本最小。迭代结果表明,两种算法的结果偏差未陷入局部最优,从而验证了该模型可信度与有效度。
由表2可知,平均总成本与αd置信水平成正比,与αq置信水平成反比。也就是说,在固定市场需求量时,回收品质量水平越高,则平均总成本越小。这是因为,回收品质量水平越高时,再制造的难度越小,耗费也就越少,再制造成本就越低,从而使得平均总成本越低。而在固定回收品质量水平时,市场需求量越大,则平均总成本越大。这是因为,市场需求量越大,回收品的回收数量相应越多,进而造成较高的库存水平,使库存成本增加, 从而使得平均总成本越高。而迭代结果表明,αd和αq一定的情况下,ATC最小。因此,需求量和回收品质量的恰当组合有利于降低系统总成本。
除此之外,由表2可知,无论何种情况下,Su1均小于Su2,即补贴制造商的补贴金额小于补贴第三方回收的补贴金额。因此,政府补贴制造商优于补贴第三方。
由表3和图5可知:随着原材料绿色度的增大,平均总成本先下降后上升。当原材料的绿色度水平为0.3~0.6时,平均总成本相对较小。当原材料的绿色度高于0.6时,平均总成本相对较大,不适宜企业生产运作。当绿色度水平为0.3~0.6时,补贴金额最少,应对绿色度水平为0.3~0.6的原材料进行补贴。
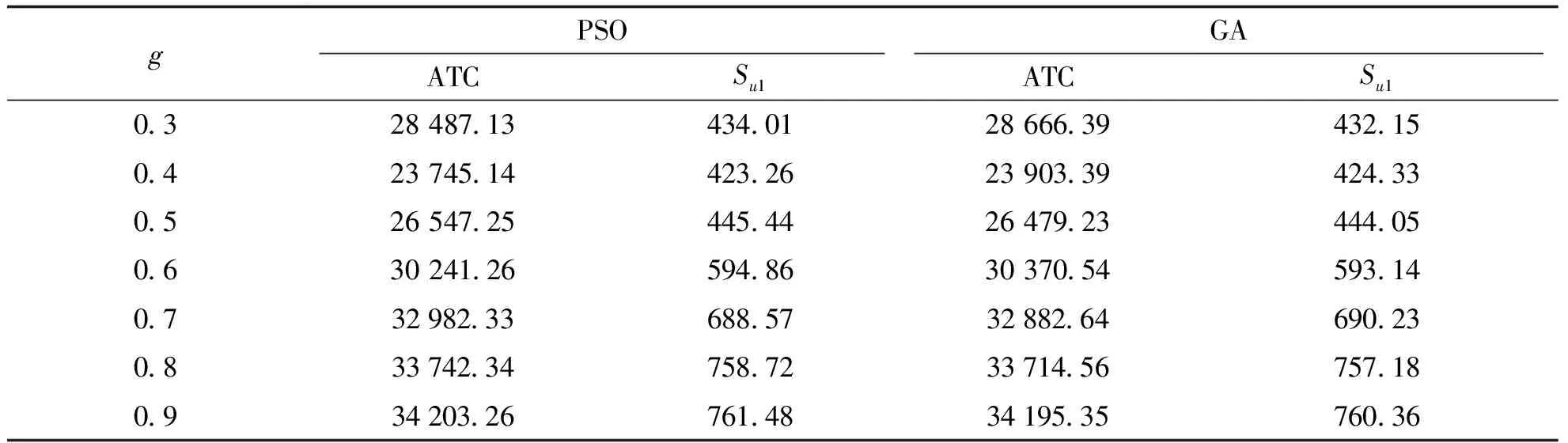
表3 不同绿色度和补贴的灵敏度分析
进一步分析,由图6可知:当回收品质量水平低于0.37时,平均总成本过高。若想提高回收率,可以回收质量水平为0.37~0.43的废旧产品。因此,考虑到提高社会效益,政府可对质量水平为0.37~0.43的产品进行二次补贴,以提高回收率。
四、结论及展望
研究了不确定环境下考虑政府补贴的双回收渠道绿色闭环供应链问题,采用模糊规划法对系统总成本的模型进行求解,并通过对计算案例的双算法求解验证了模型的可行性和有效性。主要研究结论有:需求量和回收品质量的恰当组合有利于降低系统总成本;相比于第三方回收,制造商回收渠道是占优策略;政府补贴有助于企业提高制造过程对绿色原材料的使用率以及再制造过程的回收率。
本研究可为企业在不确定环境下制定最优策略、规划企业制造/再制造活动提供借鉴,也可为政府可量化地制定和实施补贴和再补贴提供技术和理论支持。进一步的研究可以考虑补贴系数和再制造率之间的关系以及总成本和补贴系数与再制造率之间的关系等问题。

