面向非平衡与概念漂移的数据流分类的研究
陈荣
(四川大学计算机学院,成都 610065)
0 引言
随着时间推移以及科学技术的发展,数据快速增长,为利用其背后巨大的经济和实际应用价值,数据流分类是其中的关键环节。传统分类问题,如VFDT[1],是基于“标准数据”进行的,所谓的“标准数据”是指那些数据分布均匀不变,类别均衡的数据集。然而,现实问题中,这样的“标准数据”并不常见,更多是“非标准数据”,而解决此类数据的分类问题才更有意义。
相较于传统数据的静态环境,数据流的产生环境是非静态且变化的,在这样的环境中,数据分布会随时间发生变化,这就产生了“概念漂移”现象。处理这类问题,已有多种算法[2-3]。另外,真实数据流中越来越多的非平衡数据流,例如入侵检测、癌症筛查等。如Learn++.NIE[4]、Learn++.NSE[5],都用于解决该问题。
综上,为解决流分类中同时存在的概念漂移以及类别不平衡问题,本文设计了一种利用部分标签数据,使用监督与半监督结合的形式进行的数据流分类方法。其主要为,在检测到概念漂移之后,根据概念漂移的类型,分别使用不同的处理算法进行模型再训练,以便后续数据流进行分类。与使用全标签数据相比,这种使用少量标签数据对存在概念漂移的非平衡数据流进行分类的方法,可以获得相当甚至更好的性能。
1 相关概念
1.1 概念漂移定义
在动态的数据产生环境中,随着数据量的增加,形成了数据流。同时,数据流的分布也会随时间或其他因素产生变化,因而产生“概念漂移”[6]。例如,垃圾邮件问题,一封邮件是否被定义为垃圾邮件,是根据特定用户而言,并且随时间变化,同一用户对于垃圾邮件的定义也会有所不同,这就产生了概念漂移。
在概念漂移的诸多定义中,其中最为经典的定义形式,是使用概率论中的联合分布随时间变化的表达。即在t0时刻,对应的输入变量X与目标变量y之间的联合分布与t1时刻的X与y之间的联合分布之间存在差异[7]:
1.2 概念漂移的分类
基于对概念漂移的定义,结合联合分布的公式,会造成概念漂移的因素有:类的先验概率P(y),类的条件概率P(X|y),样本的后验概率P(y|X)随时间发生了变化。在实际数据流环境中,观察的重点在于是否影响了最后的分类预测[8],所以,概念漂移可以分为以下两类:
(1)实漂移:后验概率P(y|X)发生了变化,P(x)可能发生了变化,也可能没有;
(2)虚漂移:虽然P(x)发生了变化但是没有影响到最后的分类预测P(y|X)
根据数据分布的变化形式,实漂移又可以根据目标概念发生变化时,经过的实例长度分为突变漂移、渐变漂移,如图1。
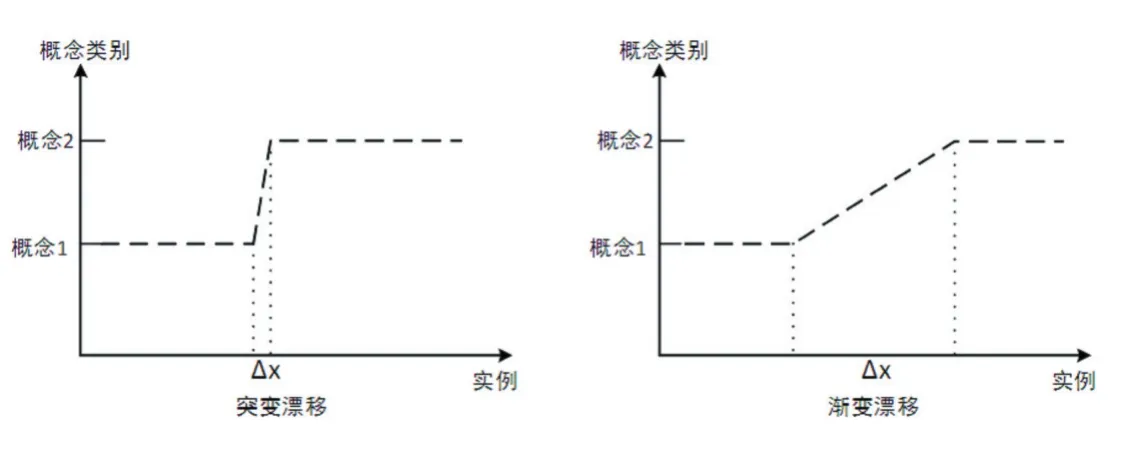
图1 概念漂移类型
1.3 非平衡数据流
在待处理的数据流中,样本比例占多数的类别,称为负类;样本比例占少数的类别,称为正类。正负类的类别数量比例悬殊,就出现了非平衡数据流。由于多数模型是在均衡数据上训练而来,因此它们在非平衡数据流上的分类效果并不理想,性能及精度都偏低。
2 基于特征样本的监督与半监督的流分类算法
非平衡的概念漂移数据流在现实场景中越来越多。为解决此类数据流的分类问题,Elaheh Arabmakki等人的RLS-SOM框架[9],虽然利用了部分标记的数据进行模型的训练,相较于其他全标记的算法,如UCB、SERA等,只用了10%-30%的标记数据就达到了同等分类性能。但是,对于剩下的大部分未标记数据并没有使用。因此本文设计了基于特征样本的监督与半监督的流分类算法,即,使用监督与半监督结合的方式,利用部分标记以及大部分未标记数据,针对非平衡的概念漂移数据流进行模型训练。
在初始化阶段,得到初始分类模型以及由特征向量SV1和正类样本PS(Positive Samples)组成的代表性样本 RS(Representative Samples)。在之后的训练阶段,计算后续数据流中的数据块di(i=2,3,…,n),与RS的欧氏距离:
选取最短距离K个样本SDK(Shortest Distance K),请求其标签。若SDK包含正负类样本且分类准确率变化超过阈值α,则判定发生了条件漂移,本文使用基于特征样本的监督式流分类算法。若SDK中不包含正类,则判定发生了特征漂移,本文提出基于特征样本的多阈值SOM非随机半监督式流分类算法。

2.1 基于特征样本的监督式流分类算法
在发生条件漂移后,由于分类边界只发生了轻微漂移,SDK还能够代表当前数据的特征,所以此时的FS(Feature Samples)就是SDK中的样本,所以,利用FS使用监督式的方式,例如DT(Dession Tree)等,重新训练并更新模型,并且更新RS。然后,进入下一轮的分类与漂移判定流程。
2.2 基于特征样本的多阈值SOM非随机半监督式流分类算法
在发生特征漂移后,由于SDK中没有包含正类,由此可知,分类边界发生了重大漂移,此时,需要在当前数据快上,重新寻找新的FS用于训练新模型。在本文中使用基于SOM多阈值样本搜索法寻找FS。算法如下:


在获取到当前数据块di的FS及其标签后,结合剩下的无标签样本,使用半监督的方式训练新的模型。在已有的基于度量聚类假设的权重学习算法的基础上[10],本文提出使用基于特征样本的非随机半监督聚类算法,通过SOM多阈值样本搜索法获得的特征样本作为初始聚类中的标签样本。算法如下:

其中,以“信息熵”为基础,本文使用“样本熵”来衡量簇的规则性CR(Ci),这里的H表示di的样本熵,H(Ci)表示簇Ci上的样本熵。



当数据块di+1到来之后,其中数据样本x的样本则以如下公式得出。
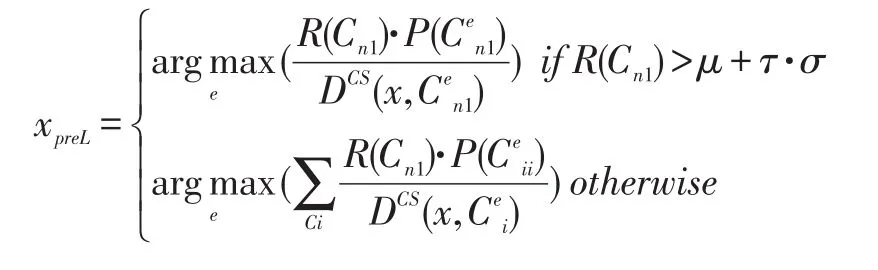
最后,获得了di+1的全部标签数据,接着使用该获得完全标记的数据块,重新训练并更新模型,并且更新RS。然后,进入下一轮的分类与漂移判定流程。
3 实验分析
3.1 实验数据集
实验数据集主要为UCI的森林覆盖数据集。完整样本有581012个样本,7个类型,54维属性。为了产生非平衡的环境,选取了其中4组2类进行实验。

表1
3.2 实验结果
本实验通过与在同样环境下的简单分类器进行分类准确率对比,简单分类器在检测到概念漂移后,均使用全标记的监督式训练新的分类器。在不同数据集上,改变每次处理的窗口大小,得到准确率变化如图2-图5。其中横坐标表示窗口的大小,纵坐标表示判定分类性能的指标Acc。
由此可见,本论文实验模型在发生概念漂移之后,只选取部分标记数据作为特征样本重新得到的分类模型在分类性能上基本能达到和普通利用全标记数据训练得到的模型一样的水平,甚至在某些特定情况下,性能更好。

图2

图3

图4

图5
4 结语
相对单纯概念漂移数据流分类来说,针对同时存在概念漂移以及类别不平衡分布的特定数据流分类的研究还较少。如何在二者皆存的情况下,及时对发生漂移的数据重新训练有效分类模型,显得至关重要。本文提出的,针对不同漂移类型,使用不同的模型再建方法,不仅对有标签数据的数量要求有降低,同时还利用了无标签的数据,并且还取得了不错的性能。

