基于旅游生产线的景区景点闲置、过载和不确定条件下容量决策分析

熊 浩， 鄢慧丽

(1.海南大学管理学院， 海口 570228； 2.海南大学旅游学院， 海口 570228)

对于包含有多个景点的景区或主题公园，学者刘益较早指出了以景点周转率为出发点的景区容量计算模型具有明显的局限性，认为景区周转率计算相比景点周转率更加合理[1].后来，学者黄羊山发表多篇论文对传统的景区容量算法进行了较为深入的分析，进一步指出了传统景区容量计算模型的错误}，并提出了基于流函数的计算模型[3]和“求小法”计算方法[4].假设游客动态匀速的移动，考虑了游览顺序、线路时间、游览时间等因素，比较合理的分析了游客在景区的容量计算问题.

近来，学者鄢慧丽和熊浩在黄羊山文章的基础上结合生产运作管理的相关理论提出了旅游生产线的概念[5]，更加合理的解释了景区容量计算的生产运作特征，并且推导出了基于旅游生产线的景区容量及准入批量的计算方法[6-7].旅游生产线理论利用生产运作理论较好的解释了为什么景区容量受周转率小的短板景点影响，为什么景区景点周转率不相等时不能取平均值，指出了景区内景点时间均衡与否和景点容量均衡与否，是导致景区容量计算复杂性的原因.同时也给黄羊山学者提出的流函数提供了更为合理的理论支撑.

然而，关于旅游景区景点闲置、过载和不确定条件下容量决策问题仍然需要进一步完善和更加深入的探讨.本文根据旅游生产线的生产批量、生产批次和总接待量公式，进一步分析了准入批量对总接待量的影响、景区旅游生产线的闲置与过载、景点容量和游憩时间不确定对容量控制决策的影响.这些问题的深入分析能更加真实准确的应对高峰期景区景点容量控制问题，从而帮助景区科学合理的进行景区景点容量设计和容量控制.

1 景区旅游生产线

1.1 景区旅游生产线的基本原理

假设一个景区包含若干个景点，将这些景点看作不同的生产工序，则景区内所有的景点构成了一条为游客提供旅游服务的生产线.在景区旅游生产线中，游客是“工件”；景点是“工序”；游客在景点的游憩时间是“加工时间”.每道工序可以进行批量加工，且景点容量就是工序的单批加工能力；旅游生产线的瓶颈工序为周转率最小的景点，称为瓶颈景点.

对于旅游景区的旅游生产线，本文引入了旅游子景点的概念对游览时间较长的景点进行分解，使景区中所有子景点的游览时间相同，从而使得旅游生产线具有相同的生产节拍.另外，为了分析的方便，本文将使用和文献[7]中相同的范例.

范例：某景区拥有2个景点，景点1的设计游览时间和容量分别为1 h和100人，景点2的设计游览时间和容量分别为1.5 h和120人，假设工作日时长为8 h.

1.2 基于景区旅游生产线的容量优化模型

假设给定某个景区有m个景点，每个景点的设计容量和设计游览时间分别为：Ci和ti，则景区各个景点的周转率为Zi=Ci/ti.如果t0为景点游览时间{t1，t2，…，tm}的最大公约数，则景点i分解后的子景点数量为ni(ni=ti/t0)，总子景点数为：

(1)

分解后各个子景点的设计游览时间都变为t0，设计容量变为：

qi=Ci/ni=t0Ci/ti.

(2)

然后，依据景区生产线顺序移动的生产周期公式，分别推导出有游览顺序和无游览顺序的景区容量控制最优决策(详见文献7).

1)有游览顺序

根据景区是否具有游览顺序，分别基于景点分解的景区旅游生产线实际上可以看作为以子景点为工序，以游客为工件的生产线.根据平行移动的生产线批量决策模型可以推导该生产线的批量、批次数和工作时间的接待量分别为：

Q0=qmin=t0Zmin，

(3)

(4)

Cmax=[T/t0-(N-1)]qmin=

[T-(N-1)t0]Zmin=

(5)

其中，qmin=min {qi，i=1，2，…，m}为瓶颈子景点对应的生产能力，Zmin=min{Zi，i=1，2，…，m}为瓶颈景点对应的生产能力，一般又称为最小周转率；Q0为批量即为旅游景区的准入游客批量，M为景区在工作时间内能够完成的批次数，Cmax为旅游景区在工作时间T内的产量即为接待量.需要注意，式(5)中当t0是景区景点的公约数时最右边才能成立，因为接待批量和接待批次都需要取整.

2)无游览顺序

无游览顺序的景区，意味着刚开始时可以允许多批旅客进入，假设游客会自动散布到各个有剩余容量的景点.后续的批量计算方法和有游览顺序的景区的批量和接待量计算方法相同.第一批进入批量为：

(6)

2 景区旅游生产线的闲置和过载分析

2.1 景区旅游生产线的闲置情况分析

对于有游览顺序的景区，从景区开放游客进入初期，直到准入M批次的游客之后，景区的各个景点才会都有游客进入；到景区当天停止营业的末期最后第M批游客依次离开景区时，景区线路中所有子景点依次开始闲置.可以看出，由于必须保证游客在营业时间内完成所有景点的游憩，并且不允许任何景点存在过载，则在期初和期末景点必然会出现一段时间的闲置.这种闲置是由于系统设置的原因造成的，不可避免，称为系统闲置.

另外，无论是否有游览顺序，都有可能存在一种由于景点周转率设置不均衡造成的闲置.这种闲置是由于景点周转率不均衡造成的，可以通过调整设计来解决，称为不均衡闲置.

以上所谓的闲置是相对景点的设计游览时间和游览容量而言的.在充分利用的情况下，景区中的每个景点的最大接待量应该等于其周转率乘以营业时长.因此，基于旅游生产线的系统闲置和不均衡闲置表达式分别为：

W0=(N-1)qmin=

(7)

Wi=T(Zi-Zmin).

(8)

式(7)是系统闲置，等于期初和期末的平均闲置时间乘以最小周转率；式(8)是周转率较大的景点的不均衡闲置，景点周转率与最小周转率的差值乘以景区营业时长.

对于景点游览时间的不均衡，由式(7)可知，景点游览时间的不均衡通过影响最大公约数t0而影响闲置率.在景区总游览时间和瓶颈周转率不可变的情况下，t0越大系统闲置越小.当景点游憩时间相同时，t0最大.而对于景点周转率不均衡，景点周转率差异直接影响了景点闲置.由式(8)可知，景区可以在周转率较小的区域设置休息区等策略，使景区中景点周转率差异尽量减少.

范例分析：时间间隔为0.5，景点1分解为2个景点，景点2分解为3个子景点，子景点周转率分别为：50人/h和40人/h.接待批量为480.但是，依据式(7)系统闲置为：(5-1)×40=(2.5-0.5)×80=160；依据式(8)可知，景点1的不均衡闲置为：8×(100-80)=160，景点2不存在不均衡闲置.此时为最优接待批量，如果想进一步提升接待批量就必须打破不均衡.

2.2 准入间隔非最大公约数时的闲置分析

对于高峰期多景点景区容量控制问题，需要考虑游客的感受，太长的等待进入时间间隔可能会让游客感觉无法接受.如果人为缩短准入时间间隔，准入批量应该如何调整？调整后对整体接待数量产生什么样的影响？

1)准入时间不是最大公约数

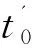
由接待量计算公式(5)可知，较小的公约数虽然会使接待批次增加，但是会使准入批量减少，从而使总接待量减少.因此，增加了景区内景点的闲置.

范例分析：景区各个景点游览时间最大公约数为0.5，现在若取0.25、0.125和0.062 5作为公约数，准入批量分别变为：20、10、5；接待量分别减少为：460、450和445.则减少率分别为：4.17%、6.25%、7.29%.实际上，公约数继续缩小到接近零时接待量的减少量为40，减少率为8.33%.

2)准入时间不是公约数

假设随意选择非公约数准入间隔时间长度t0，由于游客数必须为整数，批次数必须为整数(假设游客必须游完所有的景点)，所以利用旅游生产线进行容量控制决策时需要进行取整分析.具体的取整情况为：景点i分解后的子景点数量需要向上取整(取较大的整数)，否则游客无法完成整个景点的游玩；景区营业时间内的批次向下取整(取较小的整数)，否则最后进入的批次游客不能够完成景区所有景点的游玩.取整虽然能够保证游客完成所有景点的游玩，但是会增加景区中的景点闲置.

范例分析：景区各个景点游览时间随意选取较小的准入间隔时间为0.3，则此时景点1的分解数量为4，景点2的分解数量为5.准入批量为24，批次向下取整为18，则根据旅游生产线计算其接待批量为：432.与最优接待批量480相差48.

范例分析：景区各个景点游览时间随意选取较大的准入间隔时间为0.6，则此时景点1的分解数量为2，景点2的分解数量为3.准入批量为40，批次向下取整为9，则根据旅游生产线计算其接待批量为：360.与最优接待批量480相差120.

2.3 景区景点的过载分析

为了与闲置分析相对应，分析景区过载的情况，本文引入过载量的概念.所谓过载量是指景点在同一时刻接待的人数超出了设计容量.

根据文献[7]中旅游生产线的分析，过载的分析相对比较简单.只要景区的准入批量大于了子景点的容量上限，相应的子景点都会过载.从而，子景点对应的景点也会过载.

3 不确定条件下的旅游生产线优化分析

据上分析，对于确定条件的旅游生产线优化，只需要确定最大的公约数就能使接待批量最大.然而，对于不确定的情况，需要同时对最大公约数和准入批量进行分析.

3.1 景区中景点容量具有不确定性

当景区中景点容量具有柔性和不确定性时，如果景区景点游憩时间确定，则最大公约数不受影响.只需要分析准入批量，即分析最小的景点容量.

1) 景区中景点容量为区间数

若景区中景点容量为区间数，则可以通过概率分布函数来确定景点容量区间的下界值，从而计算出子景点容量的最小值，然后利用旅游生产线模型进行优化.

范例分析：在原范例中，若景点1的景点容量为120～150，景点2的容量为140～160，其他条件不变.准入时间间隔仍为0.5，接待批次仍为12次.此时，按照景点容量的下限值120和140进行优化，则两个景点的子景点的最小值为.因此，计算得到的准入批量变仍为40，接待量仍为12×40=480.可见，虽然单个景点的容量都增加了，但接待量仍然保持不变.

2) 景区中景点容量为随机数

若景区中景点容量为随机数，且分布已知(比如均匀分布、泊松分布或正态分布等)，则可以通过景点容量区间的下界值来寻找各个子景点容量的最小值，然后利用旅游生产线模型进行优化.

范例分析：在原范例中，若景点1和景点2的容量分别为：均值分别为100和120，方差均为10的正态分布，其他条件不变.则两个景点容量在99.87%的条件下分别为：100+3×10和120+3×10.此时利用景点容量130和150进行计算.则最小准入批量为50，接待量为12×50=600.

3.2 景区中景点游憩时间具有不确定性

当景区中景点游憩时间具有柔性和不确定性时，如果景区景点容量确定，则只需要分析最大公约数的情况.

1)景点的游憩时间为区间数

若景点的游憩时间为区间数，则可以寻找各个景点的游憩时间区间数范围内的最大公约数，进行景点的分解，然后利用旅游生产线模型进行优化.

范例分析：在原范例中，若景点1和景点2的游憩时间分别为0.8～1.2 h和1.0～1.4 h，其他条件不变.此时，选择0.8～1.2和1.0～1.4这两个区间的最大公约数1.2，此时两个景点都不需要分解.这时两个景点的游憩时间按照1.2来计算.因此，计算得到的准入时间间隔仍为1.2，接待批次为6-(2-1)=5，接待量为5×83=415.

2)景点的游憩时间为随机数

若景点的游憩时间为随机数，且分布已知(比如均匀分布、泊松分布或正态分布等)，则可以依据概率来计算景点的游憩时间，然后计算最大公约数.

范例分析：在原范例中，若景点1和景点2的游憩时间分别为：均值分别为0.9和1.2，方差均为0.1的正态分布，其他条件不变.则两个景点游憩时间在99.87%的条件下分别为：0.9+0.3和1.2+0.3.此时利用景点游憩时间1.2和1.5进行计算.最大公约数0.3，子景点周转率分别变为：25和24人/h，准入批次为：26-(9-1)=18.因此，准入时间间隔为0.3，准入批量为24，接待量为，18×24=432.

4 结论

本文对基于旅游生产线理论的景区容量问题进行了更加深入的分析.根据旅游生产线的准入时间间隔、准入批量、准入批次和总接待量等的计算公式，进一步讨论分析了批量对总产量的影响、景区旅游生产线的闲置情况、景区旅游生产线的非公约数批量对应的过载量分析以及景点游憩时间不确定情况，并得出了一些有用的结论.

1) 景区景点的闲置由两种原因造成：系统原因和周转率不均衡原因.系统原因是由于游客一定要完成所有的景点才会离开景区这种系统特征所造成的，无法避免；而周转率不均衡是可以通过设计进行改善的.

2) 如果准入时间间隔不等于各个景区景点游憩时间的最大公约数，则闲置会增大，从而减少最大接待量.

3) 景区景点的过载仅受准入批量的影响，不受准入时间间隔(游憩节拍)的影响；只要准入批量大于景区景点容量就会导致过载.

4) 景区景点游憩时间和容量不确定条件下也可以利用基于旅游生产线的容量决策模型进行高峰期的容量控制决策.

综上所述，基于旅游生产线的景区景点闲置、过载和不确定条件下的容量决策分析，能够更加科学合理地计算不同条件下的准入批量，有利于景区更好地进行高峰期景区容量控制，提高景点容量利用率.