单层石墨烯中声学极化子自陷的相关问题

侯嵩来，侯俊华

(山西师范大学物理与信息工程学院，041004，山西，临汾)

0 引言

极化子结构作为粒子与场相互作用的最简单模型，在固体量子系统、极性半导体甚至高温超导体等许多方面都发挥着重要的作用。作为晶体中的基本载流子，对解释离子晶体和极性半导体中的光学跃迁和输运现象也具有重要意义。其中极化子“穿衣”的概念已不仅限于电子－声学声子相互作用系统，更是物理学中的一个重要图像[1－4]。当电子在晶体中运动并同声子云相互作用时，电子－声子相互作用将影响迁移效应，改变如有效质量、迁移率和基态能等物理量。对于声学极化子，存在一种自陷状态，该状态的转变伴随着基态能量与有效质量的突变，同时也带来许多新的物理现象与性质。超导作为一种特殊的输运现象，低温超导微观机制正是电子－声子相互作用。低温超导BCS理论中的Cooper对也是电子与声子相互作用产生的极化子效应。现已发展许多模型用于解释高温超导的微观机制，而其中极化子－双极化子模型是BCS理论的自然延伸[5－6]。因此，研究极化子的性质有助于高温超导模型的发展和完善。

石墨烯的发现带来了许多新的物理现象及应用前景。作为一种新型二维材料，石墨烯在许多方面极具特点，给凝聚态物理带来了新的活力[7－9]。近来研究表明，2层石墨烯以1.1°扭曲在一起时会产生高温超导效应[10－11]。因此，结合石墨烯这一具体材料并研究其中极化子的自陷效应，将对包括超导在内的领域提供理论指导。

本文首先介绍石墨烯材料的特殊结构及相关哈密顿量。用Huybrechts变分法分别导出了Dirac点附近和远离该点处的极化子基态能量。通过引入电子－声子耦合常数，讨论了极化子的自陷情况。

1 石墨烯中的电子－声学声子相互作用

石墨烯作为一种二维材料，由一层排列成蜂窝状的碳原子组成。根据紧束缚近似可得其能带结构，并发现在Brillouin区的6个顶点上，石墨烯的价带与导带相连通，构成无带隙的半导体，且顶点附近的能带呈线性色散关系，这些顶点称为Dirac点。根据晶体中的有效质量理论得出该点附近的有效质量为零。因此，石墨烯中电子的运动将被无质量的Dirac方程所代替，即Weyl方程

其中c是零质量粒子的运动速度，即石墨烯中的Fermi速度。珝σ和珒p分别是二维系统中的Pauli矩阵和载流子动量。正负号分别对应不同螺旋度。本文只考虑正螺旋部分，则电子的动能可表示为

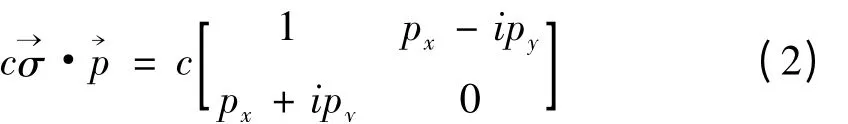
电子与声学声子的相互作用为

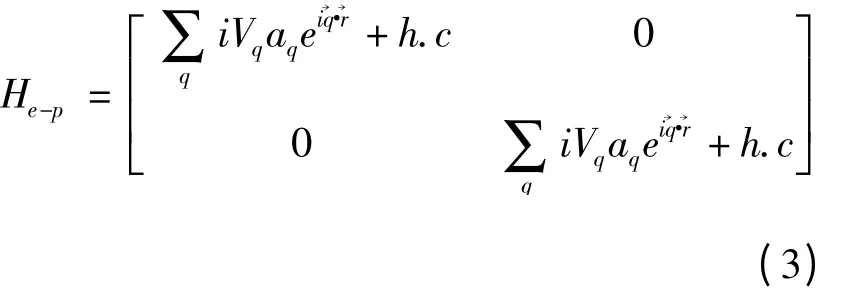
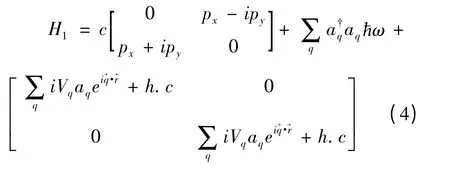
2 极化子的基态能量

为计算石墨烯体系中极化子的基态能量，采用Huybrechts变分法[13]对式(4)进行2次变换。第1次通过正则变换

引入产生与湮灭算符b↑j、bj，则动量与坐标可重新表示为

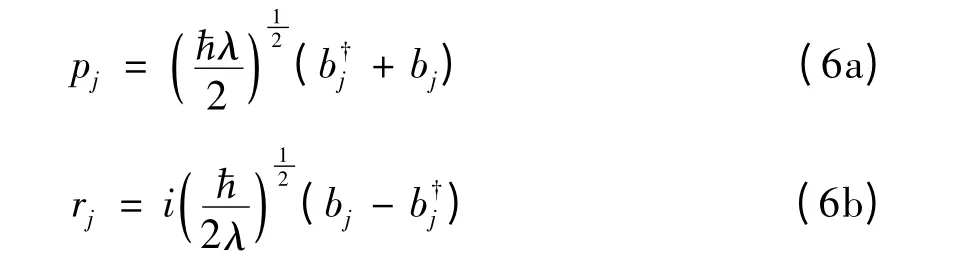
其中a和λ是变分参数。为了计算能量本征值，必须进行2次幺正变换。

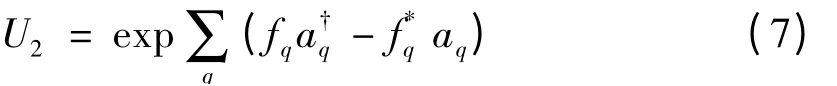
其中fa为引入的位移振幅。

考虑石墨烯中电子与零声子云组成的基态，对2次变换后的哈密顿量取平均可得极化子的基态能量为

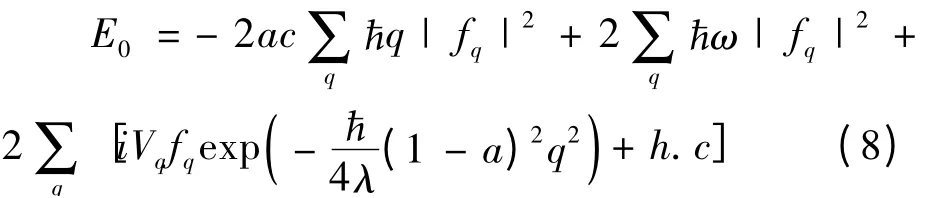
根据对称性可得，位移振子表示为

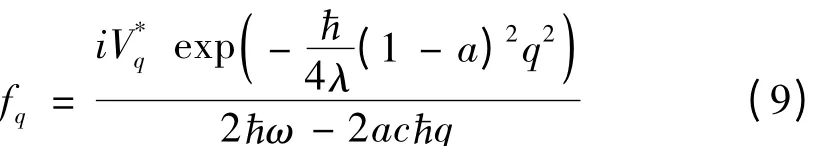
将该表示带入(8)中并采取标准化处理得

再将Vq的表示带入得基态能量，有

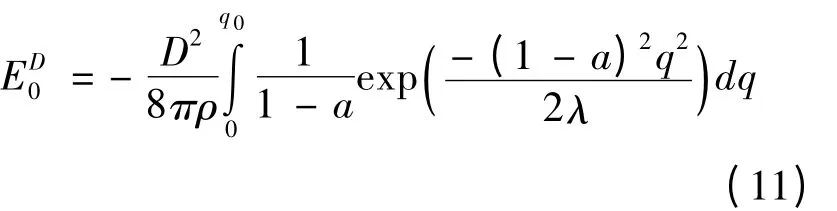
当电子远离Dirac点时，电子－声学声子相互作用可由形变势理论得[12]:

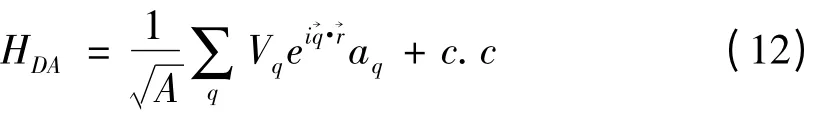
则该体系下哈密顿量表示为

通过引入无量纲常数

再次运用Huybrechts变分法并采用Hou的处理方法[14]，得到基态能量为

这一表示正是纯二维系统中极化子基态能量的表达式，与文献[14]所得结果一致。

3 数值结果与讨论

前面分别计算了二维石墨烯体系中2种情况下极化子的基态能量，式(11)和式(16)分别代表Dirac点处与远离Dirac点的基态能量。式(11)表明基态能量只有关于波矢的积分项，而式(16)表明能量由两部分组成:关于波矢的积分项和变分参量的常数项。基于以往对极化子能量问题的研究[15]，在Huybrechts变分法中，含有变分参量的常数项来源于电子动能项中引入动量的线性组合算符(6a)。也就是说，它代表了电子本身的特性。而波矢积分项是电子与声子相互作用的表示。自陷是电子在声子云中的束缚状态，是电子和声子以各自独立状态相耦合的结果。式(11)表明，当电子接近Dirac点时，基态能量公式中只有电子－声学声子相互作用的复合成份，即电子同晶格振动的整体耦合，而没有代表电子自身个体属性的动能项。因此，在这种状态下，电子不能形成正常的极化子，进而不会发生自陷转变。

对于远离该点的非相对论效应，仍采用截止波矢与耦合常数乘积的判据方式，运用数值方法计算了声学极化子基态能量与耦合常数之间的关系，如图1所示

图1 二维石墨烯中声学极化子的基态能量同电子－声学声子耦合常数α的关系

基于式(16)可知，当电子远离Dirac点时，表现为正常极化子行为，并从图1可得，极化子基态能量随耦合常数的增大而减小。当耦合常数增大到一定值时，能量曲线出现拐点，极化子能量突然下降，该点即表示从近自由态到自陷态的转变。将该点处的耦合常数定义为临界耦合常数αc，可以得到自陷跃迁的条件为αcq0≥0.6，这与Hou的工作[14]即理想二维系统模型中的结论是一致的。

现对狄拉克点处无法形成极化子进而无自陷转变进行解释:由于石墨烯的特殊能带结构，电子以零质量的形式存在于零带隙附近，这意味着电子具有相对论效应。而极化子是慢电子与晶格振动即声子相互作用构成的准粒子，是晶体中缓慢运动电子的一种表现属性。现以单价金属中电子同LA声子互作用的哈密顿量为例就电子的跃迁变化频率同声子频率的对应关系做简要定性说明:不计自旋，运用中岛变换[16]可得该系统中电子－声子－电子的有效相互作用为

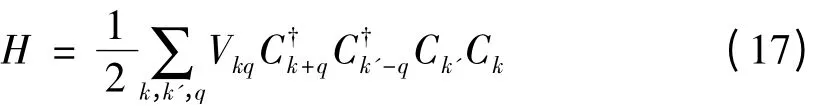
该哈密顿量为晶体中电子同相近的另一电子相互作用的表示，而作用媒介是电子对晶格的影响，即电子－声子相互作用。该式并非极化子情况下的相互作用，而是在未形成极化子时晶体中电子－声子相互作用的表现，前文关于哈密顿量的表示皆是在假定电子运动构成极化子的前提下。因此，在分析形成极化子所应满足的电子－声子相互作用时，运用该式进行说明。其中Dq为电子－

声学声子相互作用系数;Vkq符号反映晶体中两电子之间相互作用的性质，取正时电子之间相互排斥，取负时相互吸引;ωq表征晶格畸变响应电子的频率。当电子－声子相互作用，能量由εk跃迁至εk+q，其改变的快慢，即跃迁频率由ω表示。只有当声子频率大于电子的跃迁频率时，电子库仑势造成的晶格畸变才可被晶格及时响应，并导致电子周围有正电荷集中。而当电子跃迁频率大于声子频率时，电子库仑势的作用得不到及时的响应，也就不会产生围绕电子集体效应。当电子在特定结构中具有相对论效应时，由于电子的快速迁移率，晶格振动频率不能及时对电子的库仑势做出响应。这样就不可能形成由电子极化所产生的正常极化子，更不用说形成自陷态。

4 结论

本文用Huybrechts变分法分别计算了石墨烯中Dirac点和非Dirac点处极化子的基态能量。结果表明，由于狄拉克点附近电子的相对论效应，不能形成正常的极化子。在电子远离狄拉克点时，声学极化子基态能量与电子－声子耦合常数的关系符合理想二维理论的结论。即用石墨烯材料验证了二维体系中声学极化子自陷判据的合理性。