土壤水力参数对点源入渗湿润体形状的影响

苏李君 蔺树栋 王全九,3 王 康

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室， 西安 710048；2.西安理工大学理学院， 西安 710054；3.中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室， 陕西杨凌 712100)

0 引言

我国人均水资源量偏低，随着人口的增加和经济的发展，愈来愈多的地区出现水资源供需紧张的状况，北方地区的水资源已经不能支撑其经济持续健康的发展，困境日趋明显，降水更是稀少不均。面对现有水供应日趋增加的态势，特别是农业灌水对精心设计和管理的灌溉系统的需求，合理设计灌溉系统、提高灌溉用水效率显得尤为重要[1]。

滴灌技术以其显著的节水、节肥和增产等优点在我国已得到大面积的推广和应用，是目前最先进的节水灌溉技术之一。滴灌湿润体和主要根系分布区域的一致性是提高灌溉水利用效率的基础[2-3]。分析灌溉过程中不同时期的入渗趋势、累积入渗率以及湿润锋的迁移距离，可促进灌溉系统的合理设计[1]。滴灌地表积水区(或称饱和区)对土壤湿润区的影响很早就被研究者所关注[4-7]，它对土壤湿润区有显著的推动作用。在滴灌技术设计中，土壤湿润区是确定土壤水平湿润锋运移距离与垂直湿润锋运移距离比值(简称“湿润锋比”)、灌水定额、以及滴头间距等参数的基础[8]，不少学者一直在探究滴灌条件下土壤水分运动的运移机理。一般认为，当供水强度小于土壤入渗能力时，地表不形成积水；但当供水强度超过土壤入渗能力后，地表形成积水，并同时产生径流[9]。此外，FU等[1]还根据实验数据提出了累积入渗量和湿润锋运移距离的模型，研究结果可为灌溉系统的设计提供理论支持，提高灌溉用水效率。胡和平等[10]在地表滴灌条件下，运用SWMS-2D 模型对滴头流量、土壤初始含水率和饱和导水率等多种湿润体运移情况进行模拟分析，同时建立了土壤湿润体运移的经验方程。以上研究表明，滴灌水分入渗规律在灌溉系统中起到非常重要的作用，但是目前关于滴灌积水入渗模型仍需要进行深入研究，尤其是能够描述点源积水入渗机理的模型对研究滴灌土壤湿润区变化规律更为重要。因此，研究点源积水二维入渗条件下湿润锋运移规律对充分发挥滴灌的技术优势具有重要意义。

在前人研究的基础上，本文以达西定律和质量守恒原理为基础，假设湿润体形状和湿润锋比不随时间变化，仅湿润体大小随时间的增加而发生变化，在此基础上建立一个基于土壤水力参数的二维湿润锋运移模型。采用HYDRUS-3D软件模拟二维积水入渗的水分运动过程。通过软件模拟与数据分析，在研究湿润锋运移随时间变化规律的基础上，建立点源积水入渗情况下湿润锋比以及水平湿润锋与土壤水力参数间的模型，并对模型进行验证。

1 模型构建和研究方法

1.1 数学模型

1.1.1土壤水分运动模型

在膜下滴灌条件下，土壤水分运动属于三维土壤水分入渗问题，但可简化为二维问题来考虑[11]。根据达西定律、质量守恒定律，在忽略温度、空气阻力以及土壤水滞后效应等因素对土壤水分入渗影响的同时，并假设土壤为各向同性，入渗模型可简化为以积水中心为对称点的二维入渗，此时土壤水分运动可用二维Richards方程表示为

(1)

式中θ——体积含水率，cm3/cm3

t——时间，min

x、z——空间坐标值，cm

D(θ)——非饱和扩散率，cm2/d

K(θ)——非饱和导水率，cm/min

1.1.2土壤水力模型

HYDRUS-3D是一款用于模拟二维、三维土壤水分运动、溶质运移、根系吸水及热量传输的有限元计算软件。本文选取HYDRUS-3D中二维土壤水分运动模拟模块，该模块在进行数值模拟时，需要土壤水分特征曲线的参数，主要包括土壤滞留含水率、土壤饱和含水率、土壤形状参数、土壤进气吸力、饱和导水率以及土壤孔隙连通性系数。土壤水力特征模型采用Brooks-Corey模型，即

(2)

(3)

其中

m=3n+2

式中Ks——饱和导水率，cm/min

n——形状系数m——参数

S——有效饱和度

θr——滞留含水率，cm3/cm3

θs——饱和含水率，cm3/cm3

h——土壤吸力，cm

hd——进气吸力，cm

选取表1中的土壤模拟积水半径为1 cm的二维积水入渗过程，根据模拟得到的数据分析并构建相关数学模型，土壤水力参数选取HYDRUS-3D软件中自带参数[12]，见表1，表中θ0为土壤初始含水率。

表1 土壤水力参数Tab.1 Soil hydraulic parameters

为了验证本文构建模型的准确性，另采用不同的土壤水力参数对所建模型进行验证，选取土壤参数方法是在表1中相应土壤水力参数的基础上通过合理调整n和hd获得，见表2。

表2 验证采用的土壤水力参数Tab.2 Soil hydraulic parameters verified

注：*表示调整参数后的土壤类型。

1.1.3模型设定与时空离散

HYDRUS-3D工作空间的几何模型设为X-Z平面，所建模型区域为100 cm×100 cm的正方形平面，入渗源为半径为1 cm的积水区域，位于上边界中心点位置处。如图1a建立直角坐标系。

建立几何模型后将Brooks-Corey模型作为土壤水力特征模型，不考虑水力滞后效应。模拟初始时间为0 min，结束时间为2 000 min。设置最大迭代次数(Maximum number of iterations)为10 000次，设置初始时间步长(Initial time)0.5 min，最小时间步长(Minimum time)0.1 min，最大时间步长(Maximum time)1 min，含水率允许最大误差限(Water content tolerance)0.001 cm3/cm3，压力水头允许最大误差限(Pressure head tolerance)1 cm。采用HYDRUS-3D中FE-Mesh模块对所建的二维模型进行网格划分，网格划分的类型为三角形，有限元栅格划分参数中设置其有限元三角形外接圆最大直径为1 cm，其他参数采用HYDRUS数据库中自带数据。为了提高模拟结果的精度，对积水周围的部分区域网格进行加密处理，有限元计算网格如图1b所示。

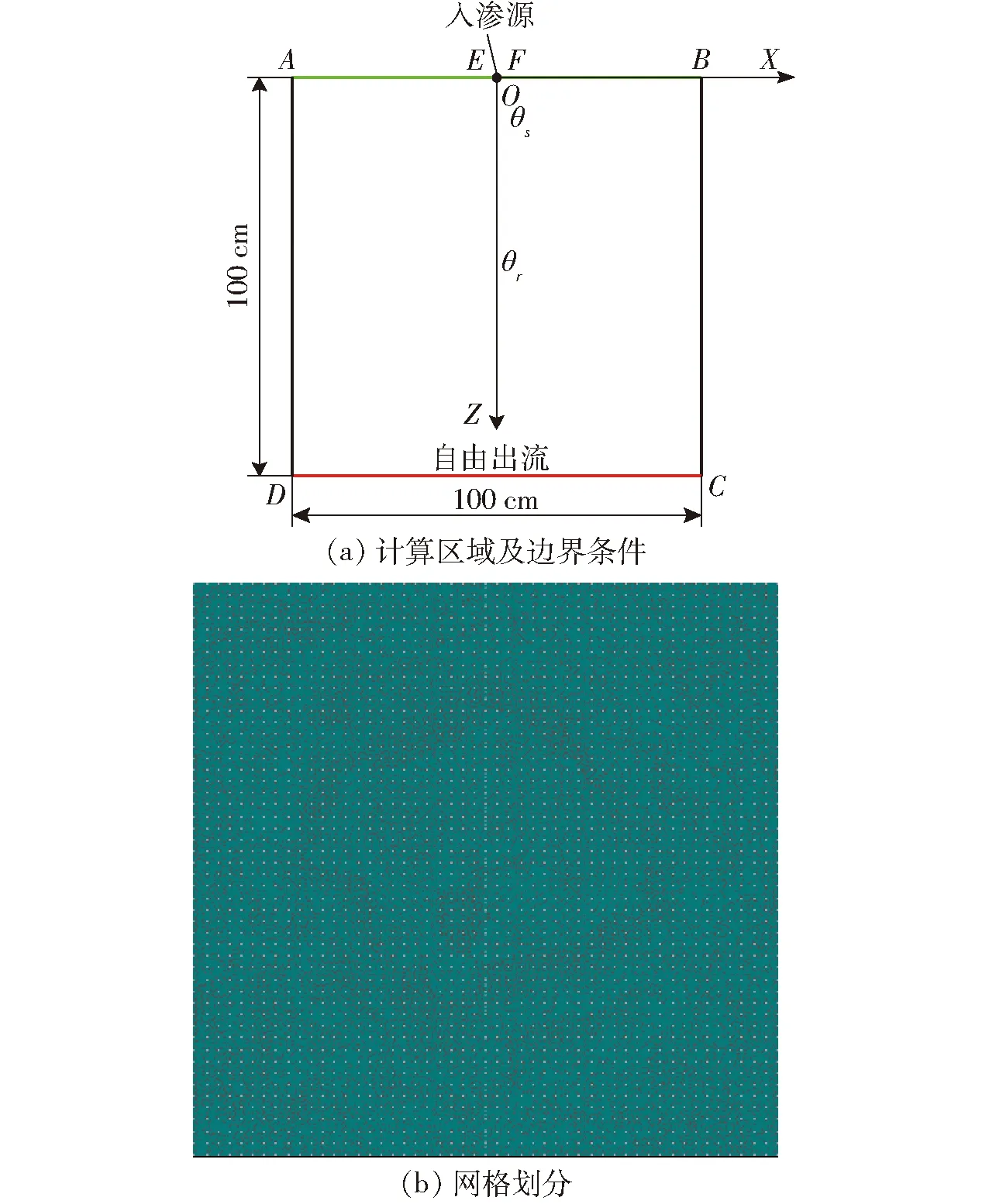
图1 计算区域及网格划分Fig.1 Simulation areas and meshing

计算区域入渗面EF是半径为1 cm的积水面，在不入渗时视地表为大气边界，入渗开始后很快达到饱和，视为定水头边界；入渗面EF左右两侧边界，以及边界AD和BC假定为零通量边界，故其水分通量为零；下边界CD为不受地下水位影响的自由出流边界。在入渗开始时，即在t=0时刻，土壤含水率为土壤初始含水率θ0。综上所述，其初始条件和边界条件可总结为：

(1)初始条件

初始条件为

θ(x,z,0)=θ0
(-50 cm≤x≤50 cm，0 cm≤z≤100 cm)

(4)

(2)边界条件

入渗面EF边界

θ(x,z,t)=θs(x0≤x≤xl，t>0)

(5)

CD自由排水边界

(6)

AE、FB、AD、BC零通量边界

(7)

式中x0——积水区域左边界，cm

xl——积水区域右边界，cm

1.1.4土壤湿润体形状模型

湿润体的大小与形状对作物生长起关键性作用，土壤水分入渗湿润体的研究是滴灌以及涌泉根灌技术要素和水分运动规律研究的基础[13]。研究表明积水入渗的湿润体形状可近似看成一个椭球或椭圆面[14-16]。针对二维土壤积水入渗问题，本文假设土壤湿润体是以垂直湿润锋和水平湿润锋为长半轴和短半轴的半椭圆面

(8)

式中xf——水平湿润锋长度，cm

zf——垂直湿润锋长度，cm

1.1.5湿润锋运移模型

土壤湿润锋分布一方面可以反映灌溉水量是否满足灌溉要求，另一方面可以反映灌溉质量，其运动规律是灌溉管理的理论基础。不同灌溉技术因湿润土壤的方式不同，湿润锋运移规律存在明显差异，而同一灌溉技术条件下，又因土壤理化性质、灌溉参数以及土壤水力参数的不同，湿润锋运移也不一致[3]。研究表明积水入渗的湿润锋运移过程可采用入渗时间的幂函数表示[14,17-18]，即

xf=a1tb1

(9)

zf=a2tb2

(10)

式中a1、a2、b1、b2——拟合参数

土壤水分扩散率反映了土壤孔隙度、孔隙大小分布以及导水性能，并影响土壤中水分运动状况，它是研究水盐运动规律与调控以及表征土壤水动力学的重要参数之一[19]。因此本文考虑构建饱和扩散率与幂函数参数之间的关系。土壤非饱和扩散率的表达式[20]为

(11)

令θ=θs，得到土壤饱和扩散率的表达式为

(12)

1.2 数据处理及误差分析

数据运用Excel进行处理，并用AutoCAD和OriginPro进行绘图以及Matlab进行模型验证，同时采用决定系数R2、均方根误差(RMSE)和相对误差(RE)评价指标进行误差分析，检验相关性。

2 结果与分析

2.1 土壤湿润体形状变化特征

图2 土壤入渗湿润体形状Fig.2 Soil infiltration wetting pattern shapes

以积水中心为坐标原点，用HYDRUS-3D模拟土壤水分在水平方向和垂直方向上的二维入渗，不同时刻湿润锋轮廓如图2所示。从图中可以看出，在整个入渗过程中水平扩散距离和垂直入渗深度均随着入渗时间的增加而增加，但湿润体运移速率在后期明显逐渐减小。入渗开始后土壤表层很快达到饱和，视为定水头，随着入渗时间的增加，同一土壤的湿润锋运移垂直入渗深度略快于水平扩散距离。这是由于随着时间的增长，土水势梯度减小，在基质势和重力势的共同作用下，导致土壤水向下运动能力增强，使湿润体的形状近似可以看作一个椭圆面[21]，细质土壤(hd>11 cm)的湿润体形状变化过程可以假设为以积水中心处为圆心的椭圆形，但粗质土壤(壤砂土和砂土，hd<8.7 cm)的湿润体形状变化过程不是以积水中心为圆心的椭圆形，随着入渗时间的增加椭圆中心逐渐向积水中心下方偏移(如图2k、2l中壤砂土和砂土湿润体形状)，因此本文研究所得模型适用于细质土壤。

2.2 水平湿润锋与垂直湿润锋的关系

通过数值模拟可知，土壤在不同入渗时间的湿润锋形状基本相似，但水平和垂直湿润锋长度随时间发生变化。选取砂土、壤砂土、粘土和砂质粘壤土为例，表3给出了这4种土壤湿润锋长度及湿润锋比随时间的变化过程。由表可看出，细质土壤(hd>11 cm)的湿润锋比随时间变化幅度较小，垂直湿润锋与水平湿润锋变化速率基本保持一致，但粗质土壤(砂土和壤砂土，hd<8.7 cm)的湿润锋比随时间变化幅度较大，随着入渗时间的增加垂直湿润锋变化速率比水平湿润锋变化速率较快，因此湿润锋比随时间的增加而减小，同时可以结合图2发现，粗质土壤湿润体椭圆中心逐渐向积水中心下方偏移，所以本研究主要考虑细质土壤，并假设细质土壤水平湿润锋和垂直湿润锋的比值不随入渗时间变化，令

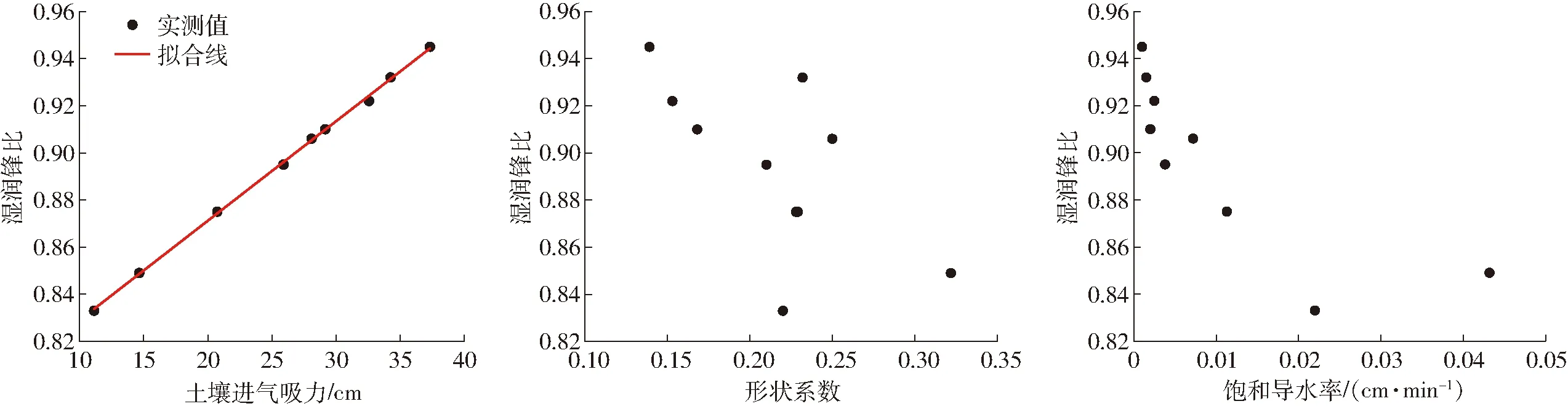
图3 湿润锋比与土壤水力参数关系Fig.3 Relationship between wetting frontratios and soil hydraulic parameters

表3 湿润锋比随时间的变化
Tab.3 Wetting frontratio varied with time

土壤类型时间/min水平湿润锋长度/cm垂直湿润锋长度/cm湿润锋比5022.46029.5300.76110025.86034.7310.745砂土20030.19552.5230.57550040.36189.0110.453100049.001134.5000.364200058.474215.0100.272509.65012.3850.77910013.20517.5880.751壤砂土20017.11523.1980.73850025.10236.5440.687100033.04854.5230.606200042.55080.5560.528504.6664.9670.9391005.5755.9220.941粘土2006.8227.2550.9405009.2299.8170.940100011.87412.6100.942200015.53616.5120.941507.0127.7620.9031008.95010.0500.891砂质粘壤土20011.60813.1100.88550016.73518.8110.890100022.36025.1820.888200030.13733.8610.890

(13)

式中wt——水平湿润锋和垂直湿润锋长度的比值，即湿润锋比

湿润锋比可以作为一个确定滴灌灌水参数的指标[22]，不同土壤的湿润锋比差异较大，分别分析湿润锋比与土壤水力参数(n、hd、Ks)之间的关系，如图3所示。由图可知，相对于n和Ks，wt与hd具有较好的线性关系，通过拟合得到wt与hd的关系为

wt=0.004hd+0.787 (R2=0.999)

(14)

结合式(13)、(14)，可得垂直湿润锋与水平湿润锋之间的关系为

(15)

由式(15)可知，在二维积水入渗条件下已知土壤某一入渗时刻水平湿润锋长度和土壤进气吸力时，就可以通过湿润锋比计算得到此时刻垂直方向上的湿润锋运移距离。

2.3 水平湿润锋运移特征

由式(15)可知，若水平湿润锋长度已知，则可以由土壤进气吸力估计二维积水入渗的土壤湿润体范围。虽然水平湿润锋长度可以直接在室内或田间试验中观测得到，但如果水平湿润锋长度与入渗时间之间的关系未知，则本文方法就不能直接预测湿润体范围。因此有必要进一步分析土壤水平湿润锋长度与时间的变化关系。不同土壤湿润体水平湿润锋长度随时间变化如图4所示。可以看出，积水入渗条件下湿润锋长度与时间存在显著的幂函数关系，这与其他学者的一些研究结果相同[14,17-18]。对表1中细质土壤的水平湿润锋长度运用式(9)进行拟合，结果如表4所示，决定系数R2均大于0.990，拟合效果较好。

图4 水平湿润锋长度随时间的变化曲线Fig.4 Variation curves of horizontal wetting front with time

表4 水平湿润锋长度拟合结果
Tab.4 Horizontal wetting front fitting results

土壤类型拟合结果R2粘土xf=1.260t0.3300.996壤土xf=1.442t0.3880.996粉砂土xf=1.416t0.3810.999粉壤土xf=1.389t0.3770.998粘壤土xf=1.329t0.3580.997砂壤土xf=1.679t0.4240.999砂质粘土xf=1.330t0.3570.998粉质粘土xf=1.205t0.3270.996砂质粘壤土xf=1.490t0.3930.999粉质粘壤土xf=1.316t0.3440.997

对式(9)求导可得

(16)

计算得到水平湿润锋长度变化率随时间变化的关系曲线，如图5所示。

图5 水平湿润锋长度变化率随时间的变化曲线Fig.5 Changing curves of variation rate of horizontal wetting front with time

式(9)表明水平湿润锋长度随着入渗时间的增加而呈幂函数增大，由图5可以看出，在入渗初始阶段约200 min内水平湿润锋长度迅速增大，约200 min后，湿润锋长度缓慢增大。在入渗过程中水平湿润锋长度变化速率随入渗时间的增加而持续减小，在入渗初始的500 min内，下降迅速，约1 000 min后下降缓慢，基本趋于稳定。

2.4 湿润锋运移定量分析

图6 水平湿润锋运移模型参数与饱和扩散率的关系Fig.6 Relationship between parameters of horizontal wetting front migration model and saturation diffusivity

土壤水力参数是求解土壤水分运动方程的重要参数，也是建立土壤水分运动数学模型的重要基础。在研究水平湿润锋运移随时间变化规律的基础上，运用HYDRUS软件模拟的数据进行拟合研究发现，不同土壤入渗时的幂函数参数a1与土壤饱和扩散率Ds间呈线性关系，其中土壤饱和扩散率Ds可将表1中的参数代入式(12)计算得到，变化关系如图6a所示，决定系数R2=0.984，RMSE为0.017，RE为0.013%；同时，拟合发现参数b1是土壤饱和扩散率Ds的二次函数，如图6b所示，决定系数R2=0.981，RMSE为0.004，RE为0.011%，数值模拟效果较好。

经过拟合得到参数a1、b1与Ds间满足

a1=0.098Ds+1.175

(17)

(18)

联立式(9)、(17)、(18)可以推导得出水平湿润锋长度与土壤饱和扩散率间的关系，即

(19)

综合式(15)和式(19)可知，在给定土壤水力参数(包括n、Ks、hd、θs、θr)时，就可以估算得到某一时刻的水平湿润锋长度和垂直湿润锋长度。

2.5 湿润体变化过程定量关系评价

采用表2中的水力参数分别对湿润锋比与进气吸力的关系、幂函数参数a1和b1与饱和扩散率的关系、水平湿润锋模型以及土壤湿润体形状进行验证。实测值和拟合值的吻合程度运用决定系数R2、RMSE和RE评价指标来进行误差分析，检验模型的精确性。

图7是对湿润锋比和幂函数参数a1、b1的验证，由图7可以看出，湿润锋比、幂函数参数a1、b1的实测值与拟合值之间有较好的吻合度，决定系数R2均大于0.950，RMSE均不大于0.027，RE不大于0.124%，表明式(14)可以很好地用来描述湿润锋比与土壤进气吸力间的线性变化关系；式(17)、(18)可以较好地表示幂函数参数a1、b1与土壤饱和扩散率间的变化关系。

图7 模型验证Fig.7 Model validation

图8 水平湿润锋验证Fig.8 Horizontal wetting front validation

由图4、5已经得出，从1 000 min左右开始水平湿润锋长度变化速率基本趋于稳定，随着时间的推移，湿润锋运移变化规律无限趋于线性变化，也就意味着从此时开始计算值略小于实测值，而在实际研究中入渗时长并不会很长，因此只对水平湿润锋运移数学模型(式(19))前1 000 min进行验证，如图8所示。验证结果显示，其决定系数R2在0.941～0.999之间，RMSE在0.219～1.150 cm之间，RE在0.015%～0.954%之间，在一定误差允许范围内拟合效果较好。

图9是对细质土壤湿润体形状的验证，图中实测值表示水分入渗的实际湿润体轮廓线，拟合值表示通过式(8)计算得到的标准椭圆曲线。从图中可以看出，在入渗时刻50、100、200、500 min的实际湿润体形状和计算得到的标准椭圆曲线基本吻合，验证结果显示决定系数R2在0.920～0.972之间，RMSE在0.096～2.542 cm之间，RE在0.330%～5.970%之间，表明在一定的误差范围内二维积水入渗的土壤湿润体形状可近似看成一个以垂直湿润锋和水平湿润锋分别为长半轴和短半轴的半椭圆面，同时这一研究结果更加证明了其他学者[14-16]对土壤湿润体形状研究结论的准确性。

综上所述，在误差允许范围内，本研究所建立的模型可以为分析点源积水水分运移、滴灌灌水器的选择和布设以及为合理设计滴灌系统等相关问题提供科学依据。

图9 湿润体形状验证Fig.9 Wetting pattern shape validation

3 讨论

本文在Richards方程的基础上采用Brooks-Corey土壤水力特征模型，并假设湿润体形状和湿润锋比不随时间变化、积水中心为椭圆圆心的情况下推导出点源积水半径为1 cm的二维入渗湿润锋比及湿润锋长度与土壤水力参数间的数学模型。

通过数值模拟发现进气吸力小于8.7 cm的粗质土壤(砂土和壤砂土)湿润锋比随时间的增加呈递减趋势，这是因为随着入渗时间的增加，重力势作用明显，粗质土壤垂直湿润锋运移速率大于水平湿润锋运移速率。因此本研究只针对进气吸力大于11 cm的细质土壤进行了详细的研究。同时从图8可以看出，粉砂土*和粘壤土*的实测值和拟合值吻合效果相对较差，决定系数R2分别为0.941、0.961；砂质粘壤土*和壤土*效果较好，R2分别为0.975、0.966；粘土*、砂质粘土*、粉壤土*、粉质黏土*、粉砂粘壤土*和砂壤土*实测值和拟合值的吻合效果很好，R2分别为0.994、0.982、0.981、0.992、0.996、0.999。总体看来10种土壤实测值和拟合值吻合效果相对较好，引起偏差的主要因素可能是受幂函数系数a1的影响较大，对参数a1验证发现，实测值与拟合值并不完全一致，部分验证点分布在直线y=x两侧而并没有落在直线上。

已有学者通过试验得到，滴灌条件下湿润锋运移过程在统计学上是时间的幂函数[5,22-24]。也有不少学者根据水量平衡原理以及地表积水的原理，建立了以滴头流量与土壤入渗率比为基础的积水半径数学模型[7,25]，该模型认为滴灌条件下积水半径与滴头流量和土壤入渗率之间比值的0.5次方成正比。赵晔等[26]以水量平衡原理为基础，引用考斯加科夫土壤入渗公式建立点源积水半径运移的数学模型，发现积水半径随积水时间呈幂函数增大。另外，张勇勇等[27]利用HYDRUS-2D模拟不同土壤物理性质(土壤类型、初始含水率)、耕作技术参数和灌水技术参数组合的垄沟灌土壤水分入渗过程，采用空间矩分析方法定量分析不同因素对入渗湿润体特征量的影响，发现初始含水率对湿润体特征量的影响较其他因素小，土壤质地对湿润体特征量的影响差异明显。白雪儿等[28]对不同初始土壤含水率和滴头流量下滴灌土壤湿润体特征研究发现，再分布后的湿润体体积主要受灌水量的影响，可以选择较小的初始含水率及较大的滴头流量以提高湿润体内水分有效性。范严伟等[29]运用HYDRUS-2D 对水平微润灌湿润体模拟进行分析研究发现，土壤质地对湿润体特性有显著影响，土壤质地越黏重，湿润锋运移速率越慢，湿润体体积越小，其“圆心”越靠近微润管，同时还发现在确定的土壤质地条件下，初始含水率和压力水头对湿润体特性有较大影响，湿润锋运移距离及湿润体体积均随土壤初始含水率、压力水头的增大而增大。

综上所述，积水半径、土壤质地、土壤初始含水率和滴头流量是影响湿润体的主要因素，本文基于积水半径为1 cm的数值模拟结果较好，建立了水平湿润锋长度、湿润锋比与土壤水力参数间的关系，通过此关系可以估算土壤湿润体范围，在一定程度上可以为分析点源积水运移问题提供科学依据。但由于数值模拟时假定土壤质地均匀，初始含水率等在一定理想条件下进行，与实际自然环境状态下的土壤结构存在一定程度的差异，入渗受到土壤空间异质性、作物生长以及气象因素的影响比较复杂，因此所得结论还需通过室内和田间试验进一步验证完善，同时在后期工作中会对积水半径、初始含水率的影响以及同时适用于细质土壤和粗质土壤的几何模型等进一步深入研究，以便于对模型进行优化和完善。

4 结论

(1)所建数学模型湿润锋比与进气吸力呈线性递增关系，模型简单、便于应用，且幂函数系数和指数可以分别用土壤饱和扩散率的一次多项式和二次多项式进行估计，决定系数R2均大于0.980，RMSE在0.004～0.017之间，RE在0.011%～0.013%之间，推导得到的湿润锋模型表征了水平湿润锋长度与饱和扩散率间的关系，经验证具有较好的效果，该模型揭示出土壤水平湿润锋长度与土壤水力参数具有密切关系。通过此模型发现，随着时间的推移，水平湿润锋增加速率在1 000 min左右开始趋于缓慢，接近于一个稳定值。

(2)建立的模型能较好地表征地表二维积水入渗规律，细质土壤湿润体是以积水中心为圆心、以垂直湿润锋和水平湿润锋分别为长半轴和短半轴的半椭圆面。粗质土壤湿润体也可以近似看成椭圆面，但粗质土壤湿润体的圆心位于积水中心下方，因此，短半轴大于水平湿润锋，长半轴小于垂直湿润锋。