基于运动过程还原法的液压支架巡检机器人位姿检测
杨学军,王然风,王怀法,李卫国
(太原理工大学 a.矿业工程学院,b.工程训练中心,太原 030024)
在煤矿开采少人化和无人化[1-2]进程中,液压支架位姿和直线度的正确性是保证工作面能够自动连续推进的关键[3-4]。只有保证液压支架排成直线,才能把与之互为支点进行推拉前进的刮板输送机推直,然后才能保证以刮板输送机为运行轨道的采煤机走直线,从而把煤壁切直[5]。单个支架位姿不仅反映了整个支架群直线度,还部分反映了工作面地板地质情况和顶部来压情况。因此,国内外许多学者积极研究工作面的直线度检测和控制问题[6],有些学者以刮板输送机为主要研究对象[7-9],有些学者以液压支架为主要研究对象[10]。
澳大利亚的LASC技术[11-12]是通过在采煤机上安装三维陀螺仪和惯性导航仪,得到采煤机机身的运动速度、姿态和位置信息,利用行走轨迹判定刮板输送机的轨道直线度,进而通过液压支架调整刮板输送机的位置,实现直线度控制。基于视觉的刮板机直线度测量方法[13-14]通过控制刮板输送机溜槽上安装的LED灯点亮和熄灭,利用摄像仪测量计算每节溜槽偏移度。基于超声波传感器测量千斤顶位移量的刮板输送机调直方法[15]采用超声波传感器测量千斤顶位移量并传输至控制台,经数据比对后,自动调整刮板输送机的直线度。
基于激光对位传感器测量液压支架相对位移的直线度控制方法[16-17]是在每台液压支架上各安装一个激光对位传感器,根据传感器输出值进行支架移动量控制。基于LabVIEW的矿用液压支架姿态监测系统设计[18]是利用激光测距传感器测量液压支架底板与顶板的距离以及对支架顶板的姿态,实时显示液压支架的高度变化和顶板姿态变化。
上述研究工作均取得了一定的成果,但是还存在着一些问题:1) 在检测工作面直线度的过程中没有一个固定参考体系,只检测到了自身的直线度,没有检测工作面与开采方向是否垂直,等等[19];2) 为了适应检测方法,需要改造被检测对象,需要在液压支架上安装大量的位置和姿态传感器,这样会造成大量前期改造费用和后续维护费用;3) 通过检测相邻支架位姿关系来推算所有支架位姿关系及直线度的方法,有一定的累积误差[20];4) 对液压支架进行6个自由度位姿检测的研究尚未见文献报道;5) LASC技术由于涉及军工产品禁运及价格昂贵等问题,在国内的推广使用受到一定的限制。
王国法[21]总结了基于支架相对位移的工作面直线度控制方法后认为:可以选取激光传感器作为所有支架相对位移的参考,将其发射端安设在工作面的一端支架上,其他支架都安装有接收装置。每个支架的相对位置均与安装有发射端的支架位置相比较,这样工作面整体直线度就有一个统一标准。
1 液压支架位姿检测方法
1.1 支架位姿描述方法
描述刚体位姿的方法很多。本文借鉴描述船舶在航海时姿态的RPY角法,采用运动过程还原法对液压支架的位姿进行描述。
一个刚体在空间有6个自由度,只要这6个自由度已知,则其在空间的位置和姿态就会唯一确定。设液压支架群首架上固接的绝对坐标系为{H},待测支架上固接的相对坐标系为{S},则{S}系相对于{H}系的位姿可以这样来描述:刚开始时两个坐标系完全重合;经过了一系列复杂运动后{S}系到达了某一位姿。现在不考虑其具体运动过程,认为目前任何位姿都可以通过6次有序运动到达,即首先绕{H}系的X轴、Y轴、Z轴各旋转一定的角度(θ,φ,ψ),再沿相应坐标轴各平移一定距离(u,v,w),最后到达了现在的位姿(如图1所示),此时就可以分别用6个有序数列来表示这两个坐标系。

图1 支架位姿形成过程示意图Fig.1 Schematic of support pose formation process
设{H}系位姿为(0,0,0,0,0,0),则{S}系相对{H}系的位姿就可以表示为:
LOC(S,H)=(θ,φ,ψ,u,v,w) .
运动过程还原法采用从一个坐标系到另一个坐标系的6个运动参数来描述两个坐标系的相对位姿,把运动和位姿有机地联系起来,以便以后在三维虚拟环境下还原再现各液压支架位姿和运行情况,从而进一步实现工作面支架位姿信息的透明化,并为调直支架直线度提供更全面的信息。
1.2 支架位姿检测方法
综上所述,本文提出了一种液压支架位姿和直线度检测方法模型,如图2和图3所示。
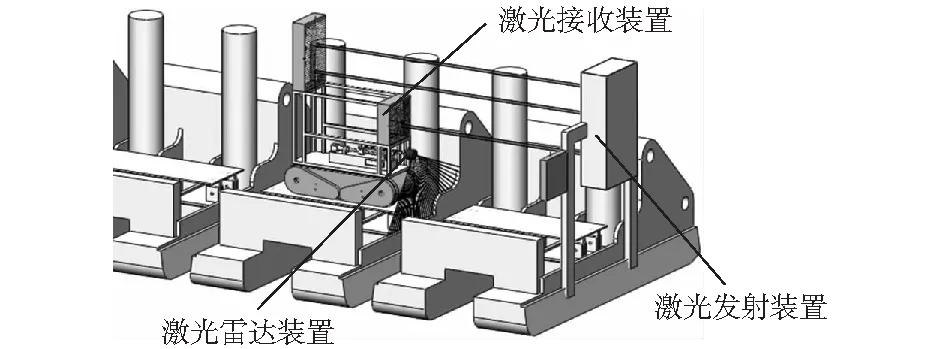
图2 液压支架位姿及直线度检测三维模型Fig.2 3D model for measuring the pose and straightness of hydraulic supports

图3 液压支架位姿及直线度检测平面模型Fig.3 Planar model for measuring the pose and straightness of hydraulic supports
该检测模型选取工作面两端支架作为所有支架的固定基准,其上各安装一个激光发射装置和激光定位装置以形成一组固定的参考激光束。在一个巡检机器人上安装有一个激光接收装置(检测自身绝对位姿)和一个激光雷达装置(检测支架相对自身位姿)。机器人检测液压支架位姿及直线度的流程如图4所示。
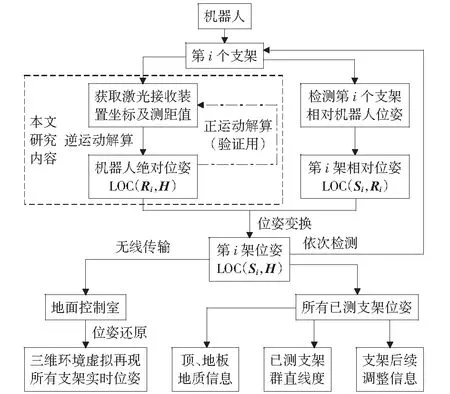
图4 液压支架位姿及直线度检测流程Fig.4 Pose and straightness measurement process of hydraulic supports
设机器人坐标系为{R}.机器人行走在第i个支架人工行走平台上时,采集自身携带的激光接收装置坐标值及距首架的距离值解算出机器人绝对位姿(逆运动解算)为LOC(Ri,H)=(αi,βi,γi,ai,bi,ci);用激光雷达装置检测出待测支架相对机器人的位姿为LOC(SiRi)=(δi,εi,ζi,di,ei,fi);通过位姿转换,得到第i个支架绝对位姿为LOC(Si,H)=(θi,φi,ψi,ui,vi,wi).完成位姿和直线度检测后,把所有支架位姿信息实时传输给地面控制室,就可以在地面控制室还原井下所有支架的实时位置和姿态,并对如何调整支架位姿和支架群直线度做出决策[22]。
该检测方法在基本不改造液压支架结构的前提下,以激光束为统一参考基准,对支架位姿和直线度进行检测,所获得的直线度信息没有累积误差。另外,巡检机器人还可以携带摄像头及其他传感器,给工作面外的人员提供视频图像和数据,以便他们及时了解工作面的情况。
1.3 巡检机器人行走机构
行走在液压支架上的机器人,除具备防爆防尘等要求外,其主要功能是能携带检测装置,识别和跨越两个支架之间的沟壑,完成每个支架的位姿检测。本文设计的巡检机器人行走机构为六履带四摇臂移动底盘。履带机器人[23-25]结构简单,故障率低,是煤矿理想的机器人行走机构,可以通过前后四个独立摇臂与主体履带的配合来越过支架之间的沟壑[26-27]。
本文主要以激光接收装置和激光测距仪的检测值为依据研究巡检机器人位姿的检测和解算。
2 巡检机器人位姿检测及解算
2.1 激光接收装置结构设计及坐标系建立
本文将在前期激光定位矩阵研究[28-29]的基础上,对激光接收装置进行设计研究。
对于在液压支架上行走的机器人,需要在其上安装激光接收装置,以便参考从首架发射的激光束来检测自身位姿。如图5所示,首架上安装的激光发射装置由两个激光发射器L2、L3和一个兼有测距和发射激光两种功能的测距仪L1组成。

图5 激光发射装置和激光接收装置结构模型Fig.5 Structural model of the laser launching device and the laser receiving device
将这三个仪器平行安装在液压支架群的首架和尾架(当机器人从首架向尾架移动时参考首架激光,反之参考尾架激光),且处于同一垂面,L1和L3相距300 mm,L2和L3相距200 mm.将激光接收装置安装在巡检机器人上;该装置由两个平行的光敏电阻矩阵面板组成,两者相距700 mm,前面低的为第一面板,后面高的为第二面板。当机器人在液压支架上从首架向尾架移动时,激光接收装置可以检测到三束激光投射在两个面板上的激光点的坐标,同时激光发射装置检测第一面板与其距离。
固定激光束是由激光发射器发射的散射度很小的点状激光线形成,主要起着固定参考作用。激光接收装置通过安装在其上的若干个光敏电阻形成的矩阵来指示激光照射的坐标,从而确定其相对激光束在径向的偏移量。
如图5所示,在这个模型中共有三个坐标系,其中OXYZ为首架绝对坐标系{H},其余两个为相对坐标系;O1X1Y1Z1为第一面板的坐标系{R},同时也是激光接收装置和机器人坐标系;O2X2Y2Z2为第二面板坐标系{E},其与{R}系有固定位置关系;O3点是O1点在第二面板的投影点。现有三束激光沿X轴照射到这两个坐标系上,由此可以获得这三个激光束的坐标值。
A点是L1照射在第一面板上的光斑点,B,C两点是L2和L3照射在第二面板上的光斑点,D点是L1与第二面板的虚拟交点。两个面板上的激光接收装置可以实时显示检测到的A,B,C点的坐标值。根据“六点定位原理”,只要有6个独立的已知量就可以确定机器人在空间的位姿,即只需要A点的3个坐标值、B点2个坐标值、C点1个坐标值就可以把激光接收装置(也就是机器人)的位姿唯一确定。
2.2 巡检机器人位姿的逆运动解算
机器人上安装的激光接收装置所显示的坐标可以理解为该装置是从{H}系开始,经过3次旋转和3次平移后得到的,其位姿解算过程就是根据激光接收装置的坐标来逆向推算自身是经过了怎样的3次旋转和3次平移后到达该位姿。由于3次旋转时,其结果与旋转顺序有关,因此本文认为机器人是经过了下面运动顺序形成了最终的位姿:先依次绕X,Y,Z轴旋转,再依次沿X,Y,Z轴平移。
2.2.1原始检测数据
通过测距仪和激光接收装置测到的坐标见表1.

表1 可测得的A,B,C三点坐标Table 1 Measurable coordinates of A, B and C
表1中,Ax通过激光测距仪测得,Ay和Az通过激光接收装置第一面板测得,By0,Bz0,Cy0和Cz0通过第二面板测得。
把B,C两点坐标全部转换到{R}坐标系中,则
RB=(700,By,Bz)=(700,By0,Bz0+500) ,RC=(700,Cy,Cz)=(700,Cy0,Cz0+500) .
式中,上标R表示选定的参考坐标系{R}.
根据“六点定位原理”,实际上只需要知道Ax坐标,再加上Ay,Az,By,Bz,Cy,Cz这6个坐标值中的5个就可以求解;另外一个相当于 “过定位尺寸”,其值的大小可以通过其他5个值表达出来。如果现在能多测出一个坐标值,就会给后面的计算带来一些便利,也可以利用这个值对其他值进行验算。
机器人从初始位姿(图5)开始,首先绕X,Y,Z轴旋转,旋转的角度分别为α,β,γ,如图6所示。其次再沿这三个坐标轴分别移动,移动的距离为a,b,c,如图7所示。经过这样的6次运动变换,形成了

图6 三次姿态变换Fig.6 Three changes of orientation
最后的位姿,位姿逆运动解算就是按照这个逆序进行还原求逆解。
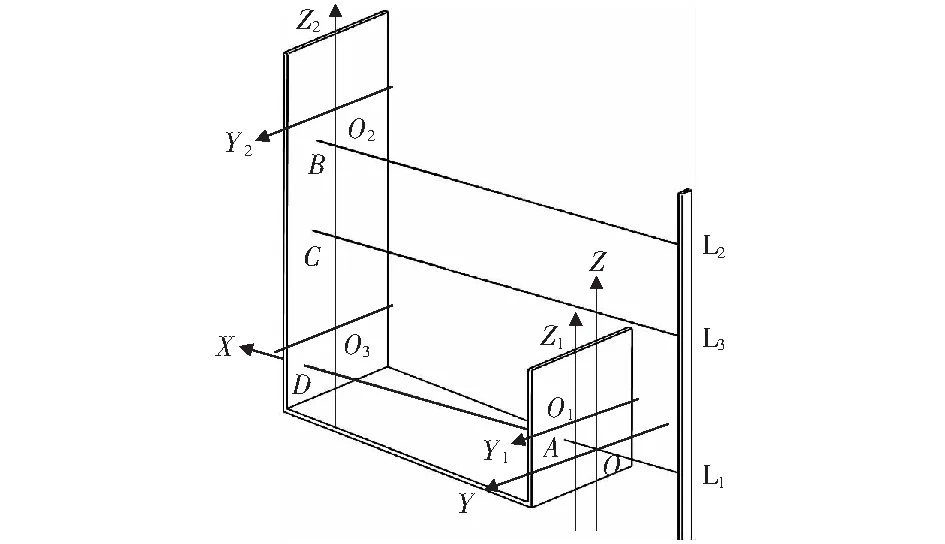
图7 三次位置变换Fig.7 Three changes of position
2.2.2解算要点
位姿逆运动解算要遵循机器人运动的逆序进行还原,即先沿Z,Y,X轴逆向平移,再绕Z,Y,X轴逆向旋转。即从图7开始,最终将机器人上的激光接收装置位姿还原为图5的初始位姿。由于解算过程比较复杂,本文分四步对主要思路和步骤进行说明,详细计算过程另撰文论述。
第一步,解算机器人沿X,Y,Z轴的平移值a,b,c.
采用坐标法求解a,b,c,具体原理如下。在{R}坐标系中,O1,A,B,D的坐标均为已知或可求;在{H}系中,A,B,D三点坐标也是已知或可求,需要求O1点坐标(a,b,c).根据同一线段在不同坐标中长度不变的原理,利用O1A,O1B,O1D三线段长度不变原理可得三个方程,解三个未知数,即为所求。
在{R}坐标系中,利用等比关系可以求出D点坐标:
RD=(700,Dy,Dz) .
其中
在{H}坐标系中,A,B,D三点坐标为:
HA=(Ax,0,0) ,HB=(Bx,0,500) ,HD=(Dx,0,0) .
其中,Ax为已知,Bx和Dx可由下式得出:
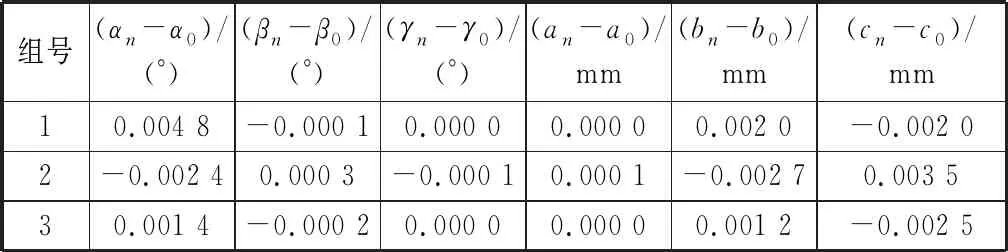
当Dz 综上得O1,A,B,D四个点在两个不同坐标系中的坐标,如表2所示。 表2 四个点在两个不同坐标系中的坐标Table 2 Coordinates of four points in two different coordinate systems mm 列三个方程,解之得: (1) (2) (当Ay<0时取负号,Ay≥0时取正号) . (3) 根据求解结果进行相应的运动和坐标还原。在{R}坐标系内平移激光接收装置使点A与点O1重合,则A,B,D三点在{R}坐标系中坐标还原为 RA=(0,0,0)=RO1,RB=(700,By1,Bz1)=(700,By-Ay,Bz-Az) ,RD=(700,Dy1,Dz1)=(700,Dy-Ay,Dz-Az) . 式中,坐标中的下标1表示还原次数,以下同。 在{H}坐标系内沿X轴方向平移激光接收装置,使得O1和O重合,A,B,D三点在{R}坐标系中坐标不变,在{H}坐标系中的坐标还原为 HA=(0,0,0)=HO,HB=(Bx1,0,500)=(Bx-Ax,0,500) ,HD=(Dx1,0,0)=(Dx-Ax,0, 0) . 至此,激光接收装置就还原为图6所示状态。 第二步,求激光接收装置绕Z轴旋转的角度γ. 采用几何向量法进行计算。在{R}坐标系内,求过A,B,D三点的平面方程;然后求解B点在平面YOZ上的投影点E的坐标;再计算过E,A,O3三点的平面方程;两平面ABD和EAO3的夹角即为γ. (当BD与Y轴交点Ey>0时取负号) . (4) 式中,A1,B1,C1和A2,B2,C2分别为平面ABD和EAO3方程的系数。 求解后,B和D点的坐标相应还原为 RB=(700,By2,Bz2) ,RD=(700,Dy2,Dz2) . 第三步,求激光接收装置绕Y轴旋转的角度β. 用几何法求解得: (当Dz2>0时取负号) . (5) 求解后,D点坐标还原为初始值,B点坐标还原为 RB=(700,By3,Bz3) . 第四步,求激光接收装置绕X轴旋转的角度α. 用几何法求解: (6) 求解后,B点坐标还原为初始值。激光接收装置同时还原为图5初始状态。 需要说明的是,文中绕X,Y,Z轴旋转的角度单位均为(°),沿X,Y,Z轴移动的距离单位均为mm. 综上,α,β,γ,a,b,c这6个参数就组成了机器人在绝对坐标系内的位姿。也就是说,机器人相当于经过了这样6次有序运动,从首架的初始位姿运动到了目前的位姿。 机器人的位姿计算完成后,需要对其正确性进行验证。本文采用两种方法进行验证:一种是正运动解算法,另外一种是虚拟装置运动模拟法。 机器人位姿逆运动解算需要A,B,C三个点的坐标值。因受激光接收装置尺寸的限制,不能任意取值,所以设计验证过程为: 1) 拟定机器人的运动过程(即机器人的位姿),如LOC(R0,H)=(α0,β0,γ0,a0,b0,c0). 2) 根据机器人运动过程,应用这两种验证方法分别得到A,B,C三点在{R}系的坐标Ay,Az,By,Bz,Cy,Cz和A点在{H}系的坐标Ax.如果结果相同,说明这两方法都是正确的。 3) 把用这两种方法得到的三个点坐标值代入位姿逆运动解算公式,还原机器人运动过程(机器人位姿),LOC(Rn,H)=(αn,βn,γn,an,bn,cn). 4) 比较LOC(R0,H)和LOC(Rn,H)的值,如果相同就说明机器人位姿的逆运动解算结果正确。 表3是拟定的三组机器人的原始运动过程数据 表3 拟定的三组机器人位姿Table 3 Proposed three sets of robot pose LOC(R0,H). 3.2.1正运动解算思路 正解算就是按照拟定的位姿参数,让机器人从初始位置开始顺序运动,从而追踪激光接收装置上A,B,C三个光斑点坐标的变化情况。即依照图6和图7运动顺序,逐步计算机器人每次运动后坐标Ax,Ay,Az,By,Bz,Cy,Cz的值。 机器人上的激光接收装置原始位姿如图5所示,其上需要计算的各点初始坐标见表4.没有列出的坐标为定值,由装置结构决定,在机器人运动过程中不发生变化。 表4 A,B,C三点初始坐标Table 4 Initial coordinates of point A, B, C mm 3.2.2正运动解算过程要点 机器人每运动一步,相应三个点的坐标值都可能有变化,所以本文仅对每一步的计算要点进行说明,略去了部分具体表达式。 第一步,绕X轴旋转α. 激光接收装置形成了新的位姿,在{R}坐标系中,有以下坐标发生了变化: By1=500sinα,Bz1=500cosα,Cy1=300sinα,Cz1=300cosα. 第二步,绕Y轴旋转β. 在{R}坐标系中,形成了以下新的坐标: 第三步,绕Z轴旋转γ. 同理,在{R}坐标系中,形成了以下新的坐标:By3,Bz3,Cy3,Cz3. 第四步,沿X轴平移a. 在{H}坐标系,Ax坐标发生改变,其余坐标无变化。 Ax4=a. 第五步、第六步,沿Y轴平移b,沿Z轴平移c. 在{R}坐标系,形成了以下新的坐标:Ay6,Az6,By6,Bz6,Cy6,Cz6.在{H}坐标系,形成了以下新坐标:Ax6. 最后,把B,C两点沿Z轴坐标转换到{E}系内: Bz7=Bz6-500 ,Cz7=Cz6-500 . 综上,Ax6为激光测距仪应检测的距离值;Ay6,Az6为第一面板应显示的坐标值;By6,Bz7,Cy6,Cz7为第二面板应显示的坐标值。 根据正运动解算公式,对表3的运动数据进行计算,得到表5的结果。该值为激光测距仪应测出的A点理论距离值和激光束L1,L2,L3落在激光接收装置上的光斑点A,B,C的坐标值。 表5 根据拟定位姿进行的正运动解算结果Table 5 Rusults of positive motion calculation using the proposed robot pose mm 图8是在Solidworks三维机械设计软件里建立并装配的位姿调整器、激光发射装置及激光接收装置虚拟模型。安装了激光接收装置的位姿调整器可以模拟机器人经过六次运动调整后,从初始位姿到达最终位姿后激光束在两个面板的坐标变化情况。把原始运动过程数据依次代入,然后测量在两个坐标面板上三个点的坐标值,就得到模拟运动的结果,该值应该与正解算结果相同。该模拟方法不需要计算公式,能真实展现激光接收装置的实际运动过程,把运动过程和位姿结果直观地联系了起来。 表6是根据表3的运动数据进行的三维虚拟装置运动模拟测量结果。 图8 用SolidWorks软件建立的位姿调整器、激光接收装置 和激光发射装置三维模型Fig.8 3 d models of pose adjuster, laser receiving device and laser launching device established with SolidWorks software 表6 根据拟定位姿进行的虚拟装置运动模拟结果Table 6 Motion simulation results of 3D digital virtual device using the proposed robot pose mm 正运动解算和三维虚拟装置运动模拟两种验证方法的结果比较如表7所示。从表中可以看出,两种方法得出的结果有一定的误差,这是由于正运动解算过程和软件模拟计算过程不尽相同,但误差均非常小,可以忽略不计。 表7 正运动解算与虚拟装置运动模拟结果比较Table 7 Comparison of positive motion calculation and virtual assembly motion simulation mm 表8是根据表5进行的机器人位姿逆运动解算结果。由于三维虚拟装置运动不能进行位姿逆运动模拟,所以只有正运动模拟结果。 表9是拟定位姿与逆运动解算位姿比较的结果。从表中可以看出,机器人位姿理论计算是完全正确的,而且具有唯一性,误差属于正常范围,可以忽略不计。 表3、表5-表9是从大量验证数据中摘录的三 表8 根据表5计算的机器人位姿逆运动解算结果Table 8 Robot pose solved by using the inverse motion formula according toTable 5 表9 逆运动解算位姿与拟定位姿比较Table 9 Comparison of inverse motion solution and the proposed robot pose 组数据,这三组数据基本代表了该装置的测量范围和检测特征。巡检机器人位姿检测理论和逆运动解算的正确性,为后续液压支架姿态及直线度检测和调整实验研究奠定了基础。 1) 提出了描述液压支架6个自由度位姿(3个位置自由度(u,v,w)和3个姿态自由度(θ,φ,ψ))的运动过程还原法。基于该方法,设计了利用巡检机器人对液压支架位姿和直线度进行检测的方法模型。该检测模型先利用激光接收装置检测巡检机器人位姿,再用激光雷达装置检测待测支架相对机器人位姿,最后通过位姿转换获得各支架位姿,进而再计算出整个支架群的直线度。用该方法模型检测支架位姿,不用在待测支架上安装任何传感器,计算得到的直线度没有累积误差。 2) 探索了利用激光束、激光测距仪和激光接收装置对机器人位姿进行检测的装置结构及尺寸。通过分析装置和建立坐标系,推导了机器人位姿的逆运动解算公式,实现了机器人位姿的运动过程还原。该机器人位姿检测方法只利用激光接收装置上3个点的6个坐标值来计算机器人的3个位置坐标和3个姿态角度,这为其他场合的位姿检测提供了理论依据。 3) 通过正运动解算和虚拟装置运动模拟两种方法验证了巡检机器人位姿检测的逆运动解算的正确性,这为后续液压支架姿态及直线度的检测和调整实验研究奠定了基础。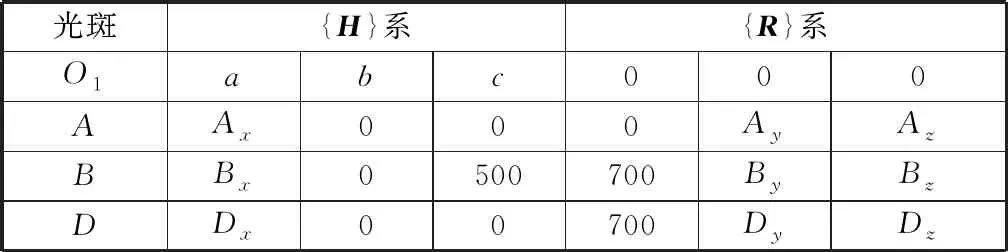



3 巡检机器人位姿解算结果验证
3.1 验证过程设计

3.2 正运动解算法验证


3.3 虚拟装置运动模拟法验证


3.4 验证结果分析


4 结论

