高热阻墙材孔型设计与热力学性能数值分析

姜 伟， 刘 丹， 杨正宏

(1.同济大学 材料科学与工程学院， 上海 201804；2.同济大学 先进土木工程材料教育部重点实验室， 上海 201804)

随着中国经济的快速发展，建筑能耗在不断增加[1]：2018年初，中国每年竣工建筑面积占世界50%以上，建筑能耗约占全社会总能耗的35%[2]，且98%的存量建筑单位面积能耗为发达国家的2至3倍[3].“十三五”规划提出了能耗总量的控制指标，对建筑节能的具体要求是大幅提升围护结构热工性能，降低建筑运行能耗，以实现围护材料耐久性、能源效率、环境效益和经济性的统一[4].另外，现实中还存在[5]烧结墙材热工性能难以满足日益增长的节能减排需求、轻质化与耐久性的矛盾等问题.国家重点研发计划项目《节能墙体材料部品化绿色制备工艺技术与装备》(2016YFC0700802)明确要求厚240mm烧结砌块的传热系数K≤0.30W/(m2·K)，孔洞率φ≥60%且抗压强度fc≥8MPa.为此，可从烧结墙材结构优化本身入手，研究围护结构热工性能的提升，同时保持其力学性能，实现轻质和耐久性的统一.

烧结砖孔型发展历经了实心砖、多孔砖、空心砖等阶段.研究[6-8]表明，空心砖的保温隔热性能优于实心砖，且条形孔优于圆形孔，孔洞率越大(孔数越多)，导热系数越小.目前，主流砖型的孔型设计不够合理，存在贯通热桥、传热系数过大等[7]问题，且对其非稳态条件下的传热分析与热-力学综合性能研究分析较少[9].因此，能同时满足大孔洞率、高热阻并具有优良力学性能的烧结墙材孔型是未来发展的方向.

现有对建筑墙体传热系数的确定方法常为试验测量(热流计法、热箱法、控温箱-热流计法和常功率平面热源法)和规范中推荐的计算公式，两者对于墙体部品传热系数的确定都有着各自的局限性.前者虽然所得数据精准，信服度高，但试验周期长、耗费投入大，并存在人为测量误差；后者使用方便，但仅局限于一维方向传热，不适用于现实中多排孔等有较为复杂构型的墙体部品.墙体部品的力学性能研究主要以抗折、抗剪强度试验为主，而多排孔试件制作耗时费力，不适合做墙体部品抗折试验，且常用的三点抗折试验法无法显示试件的整体受力情况.抗折强度作为影响墙体部品主要力学性能的因素之一[10]，数值研究方法还不够深入，且关于墙体部品热学与力学性质的耦合分析较为缺乏.数值计算方法使用快捷，可用于复杂多维墙体部品的热力学分析和非稳态传热模型研究，正逐渐被学界、工业界接受与采用.

本文在数值计算热学性质的同时，对优化设计的多排孔烧结砌块进行了抗折强度及其影响因素的数值分析，通过数值计算来研究厚 240mm 的高热阻多排孔烧结砌块热-力学性能，所得结果对自保温墙材的孔型设计指导、热力学性质研究方法优化和节能生产应用具有重要实际意义.

1 传热数值模拟计算方法

1.1 稳态传热数值模拟计算介绍

墙体部品的传热系数定义为：在稳态传热条件下，围护结构两侧空气温差为1K(或1℃)时，单位时间内通过单位面积传递的热量.用数值模拟计算方法获得墙体传热系数的方法为：在软件中建立多排孔烧结砌块墙体几何模型，对不同部分赋予填充材料和壁肋材料属性，设置分析步长和计算周期，对所有非刚体部分划分网格并定义网格单元属性，以及内外表面换热系数；通过设定模型内外两侧温度和换热系数等基本参数值，再由运行结果得到单位时间内通过的热量，从而构建一种传热系数随输出热流值变化的关系式，见式(1)：

(1)

式中：K为模型传热系数，W/(m2·K)；a、b分别为模型外、内侧温度，℃；S为模型传热面的面积，m2；Q为单位时间内通过模型传热面的热量输出值，W；l1、l2分别为模型外、内侧传热面上的宽度，m;K1、K2分别为模型外、内侧的换热系数，W/(m·K).

1.2 试验验证

1.2.1墙体传热系数的实验室检测值

本课题组对陶粒泡沫混凝土轻质砌块墙体进行了现场传热系数检测.图1(a)为所用的稳态传热性能测定系统；图1(b)为试验砌体墙，其中的标注点为温度测点(冷热面测点位置相同)[11]；图1(c)为墙体完成抹面前的效果图.墙体砌筑完成后在 (20±5)℃、相对湿度(30±10)%的环境中养护 28d，测量各标注点的传热系数(阶段 Ⅰ)；测量完成后，在墙体靠近热箱一侧抹2cm普通抹面砂浆，在同样的环境中养护28d，测量各标注点的传热系数(阶段 Ⅱ)；随后，在墙体靠近冷箱一侧抹 2cm 保温砂浆，仍然在同样环境中养护28d后测量各标注点的传热系数(阶段 Ⅲ).通过3个阶段设置的冷面温度(θL)和热面温度(θH)测试，可得到3组墙体实测传热系数KT和热阻R，如表1所示.

1.2.2数值模拟计算和验证

在陶粒泡沫混凝土轻质砌块墙体模型内外两侧分别加上不同的相互作用作为其热面温度和冷面温度，按照上述墙体传热系数数值模拟计算方法 (式(1)) ，计算了3个阶段的传热系数KS(或热阻).另外，为了验证数值模拟计算的可行性与准确性，根据GB 50176—2016《民用建筑热工设计规范》的传热系数公式，分别计算了该墙体3个阶段传热系数的规范公式解析值KC.KS与KC的对比、KS与KT的对比见表2.同时，分别以3个阶段的KC和KT为基准值，计算各阶段KS与KC、KS与KT的相对误差DA、DB，可以发现数值模拟计算值与规范公式解析值的相对误差均不超过2.1%，数值模拟计算值与实测值的相对误差均不超过10%.由此说明采用数值模拟计算方法来获取墙体传热系数是可行有效的.

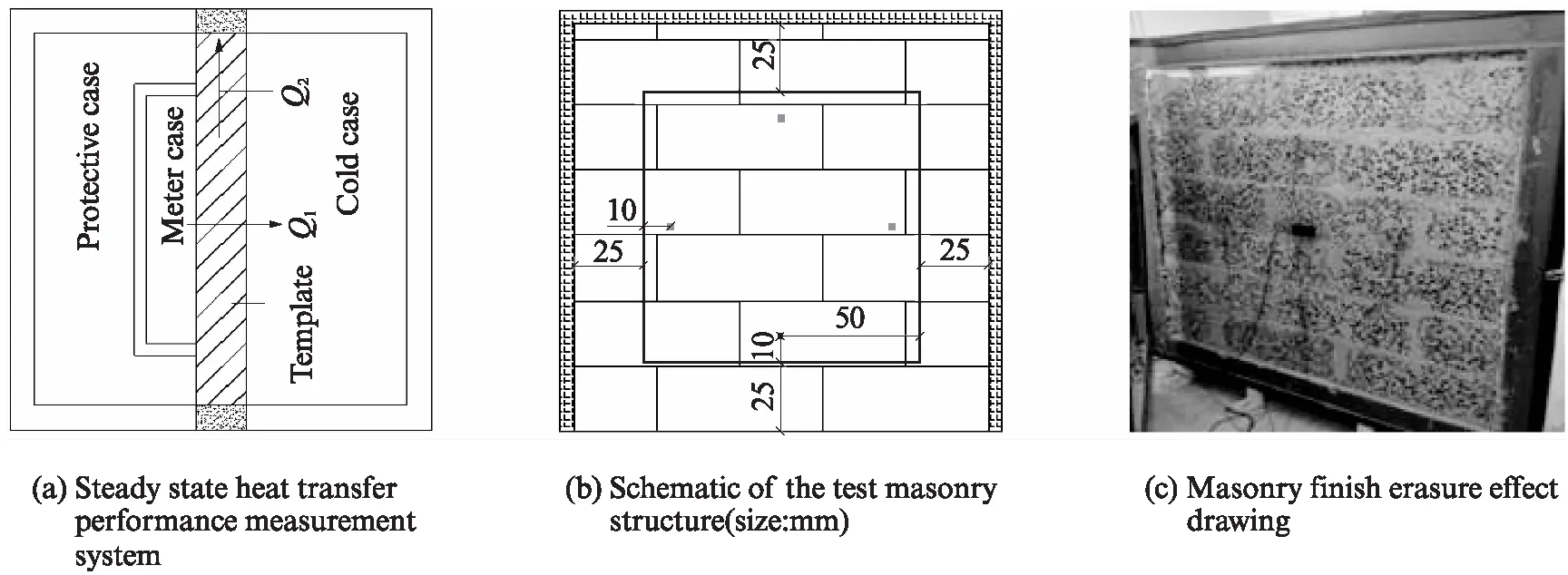
图1 试验砌体和测定系统Fig.1 Test masonry and measuring system

表1 墙体传热系数和热阻的测试结果

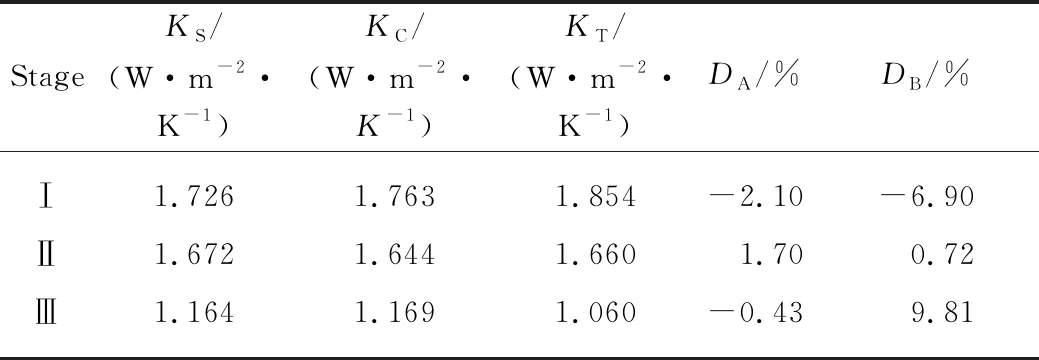
表2 采用不同方法得到的墙体传热系数对比

2 传热优化设计

2.1 3～5排孔型设计及传热系数数值模拟计算结果

某厂家以设计传热系数为0.3W/(m2·K)的厚240mm高热阻多孔烧结砌块为目标，初步设计了3排孔砌块孔型方案.本课题组对初始3排孔砌块孔型方案进行了结构优化：首先，保持孔洞率φ≥60%；其次，为了烧结砌块力学强度的需要并降低加工难度，尽量使所有标准孔和侧孔保持一致.GB 50574—2010《墙体材料应用统一技术规范》中表3.2.1规定：用于自承重墙的含孔砖壁厚和肋宽均≥10mm.根据这一规定，经过综合比较，最后设计出3～5排孔砌块的3种最优孔型，见图2和表3(为实现低传热系数目标，烧结砌块的小部分肋宽突破了上述规范的要求，相应生产工艺正在加紧研发中).

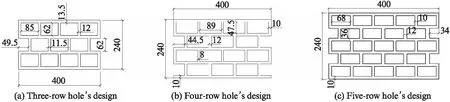
图2 3～5排孔砌块的孔型设计示意图Fig.2 Diagram of three/four/five-row hole’s block design(size:mm)

表3 3～5排孔砌块的最优孔型设计数据

在ABAQUS中模拟传热时，建立400mm×240mm的多排孔砌块模型，具体尺寸见表3.所选择的填充材料(拟用发泡聚氨酯)和壁肋材料的导热系数分别为0.030W/(m·K)和0.300W/(m·K)；边界条件设置为上面温度5℃，下面温度 -5℃，时间步设置为172800s(此时传热已达稳态)；网格为0.001m，以保持模型划分均匀、计算收敛；场定义输出NT11节点温度和HFL单元热流值，再由式(1)计算得到砌块模型的传热系数.

计算得出：3排孔砌块优化模型的传热系数为0.303W/(m2·K)，4排孔砌块最优模型的传热系数为0.268W/(m2·K)，相比于3排孔砌块优化模型下降了11.52%；5排孔砌块最优模型的传热系数为 0.174W/(m2·K)，比3排孔砌块优化模型的传热系数降低了42.57%.从满足孔洞率φ≥60%，并保持边角易成形且不易折断，同时满足传热系数 ≤0.3W/(m2·K) 要求的角度出发，可得出结论：对热学性质而言，5排孔砌块设计为最优孔型.

从多排孔砌块模型的热流分布图可以看出，热流在填充材料部分密度较小，在壁肋处密度较大，容易形成热桥.设计时应尽量避免贯通热桥，并提高孔洞率以减少壁肋热流.5排孔砌块模型的热流分布图见图3，其整体热流值(相比于3排或4排孔砌块模型)有所下降，具体表现在其传热系数较低，所以5排孔砌块模型的优势较为显著.

2.2 稳态传热系数的影响因素

首先，对同一孔型(3排孔)砌块，改变填充材料和壁肋材料种类，以研究3排孔砌块模型稳态传热系数K与材料导热系数λ的关系，结果见表4.由 表4 可知：3排孔砌块模型的传热系数随填充材料和壁肋材料的导热系数减小而减小.填充材料(拟用发泡聚氨酯)导热系数为0.030W/(m·K)，壁肋材料(拟用轻质陶粒混凝土)导热系数为 0.300W/(m·K) 时，模型整体传热系数最小.即此时模型的整体热阻最大，传热性能最好.

图3 5排孔砌块模型热流分布图Fig.3 Distribution of heat flux in five-row hole’s block

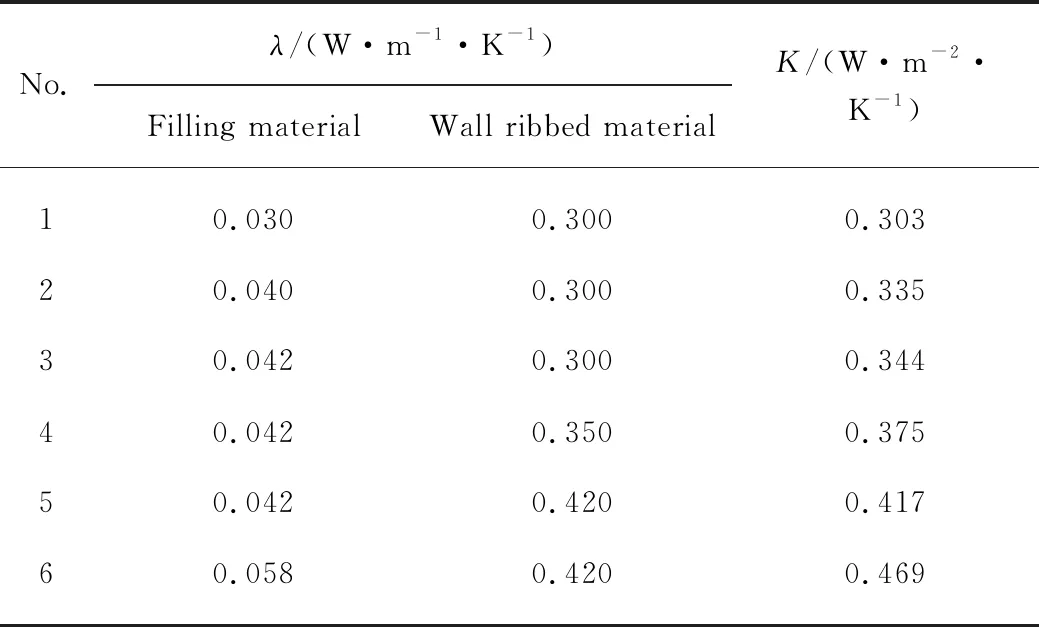
表4 3排孔砌块模型的数值模拟传热系数结果

其次，统一孔洞率63.75%，改变横壁厚度(6～ 14mm)，探究5排孔砌块模型传热系数与横壁厚度的关系，结果见表5和图4.由表5和图4可见：稳态条件下，5排孔砌块模型孔洞率统一为63.75%时，随着其横壁面积与壁肋面积之比(AHB/ABL)逐渐增加，通过壁肋的热流越来越少，而传热系数与通过壁肋热流呈正相关关系，所以此时模型的传热系数也越来越小，热阻越来越大，保温性能越来越好.

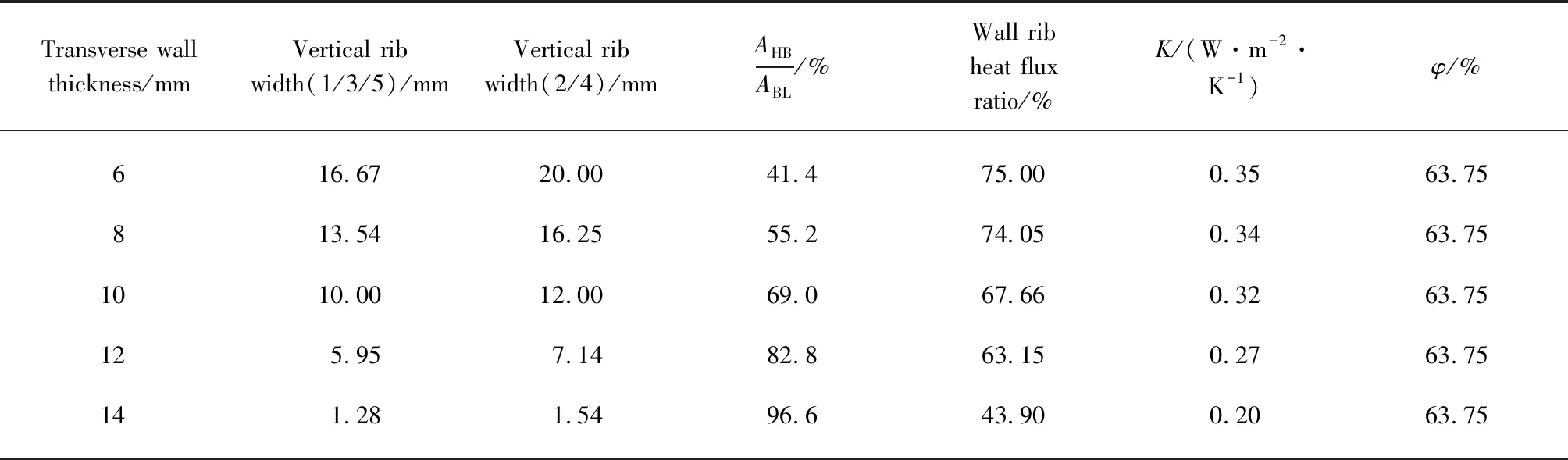
表5 5排孔砌块模型的数值模拟传热系数结果

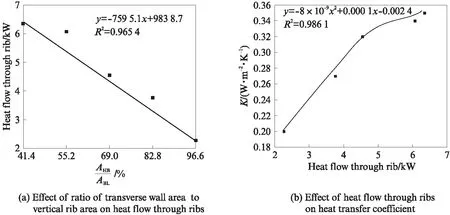
图4 稳态传热系数的影响因素Fig.4 Influencing factors of heat transfer coefficient under steady state

2.3 非稳态传热系数的影响因素

首先，在相同的非稳态(周期性非稳态)外侧环境下，探究3～5排孔砌块孔型设计对多排孔砌块模型内侧的热流分布和温度分布随外侧温度变化的影响.模型基本设置(尺寸、材料和网格等参数)见图2和表3.另外，对多排孔砌块模型的外侧温度θH(t)均设置从恒温变为周期性正弦变化函数θH(t)= 4.5+ 3.5sinωt，其中ω=2π/86400，t为外侧温度作用时间，s；内侧温度θL(t)设定为自由温度边界，只设定初始温度值；分析步长设置为129600s(1.5个周期).

数值模拟最终结果见图5.由图5(a)可见：在3种孔型砌块模型的外侧温度非稳态变化趋势保持相同的条件下，随着外侧温度作用时间增加，其内侧瞬态热流曲线都呈正弦分布，且随着排孔数增加，3～5排孔砌块模型的瞬态热流正弦函数曲线变化趋势变缓，最小值减小.由图5(b)可见：在3种孔型砌块模型的外侧温度非稳态变化趋势保持相同的条件下，随着外侧温度作用时间增加，其内侧瞬态温度曲线都呈阶梯状上升，但4、5排孔砌块模型的内侧瞬态温度变化始终明显小于3排孔砌块模型；相对而言5排孔砌块模型的内侧瞬态温度变化最小.因此，随着排孔数增加，模型内侧瞬态热流和瞬态温度所受外侧传热的影响逐渐减小，保温性能逐渐变好.

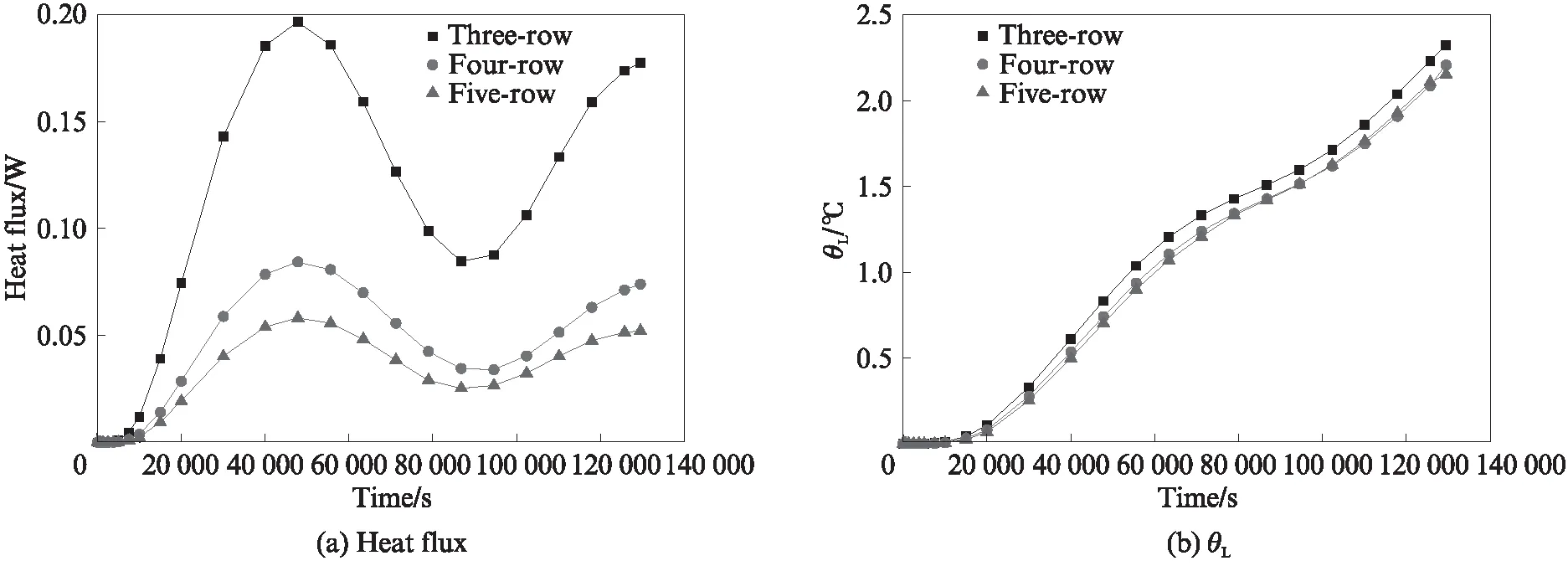
图5 非稳态下3～5排孔砌块孔型设计对多排孔砌块模型传热的影响Fig.5 Effect of three-row, four-row and five-row hole on heat transfer of block under unsteady state

其次，在墙材稳态热阻设置相同时，探究非稳态外侧环境变化对实/空心砌块模型的瞬态传热变化影响.保持2种砌块模型的稳态热阻不变(实心砌块的导热系数设为0.174W/(m·K)，参考2.1节所得5排孔砌块模型稳态下K值结果)，且设置与上述相同的外侧温度非稳态变化函数θH(t)，数值模拟计算结果见图6.

图6(a)表明，当墙材的稳态热阻设置相同时，实心砌块模型与多孔空心砌块模型在非稳态外侧环境下的瞬态热流值有差异.与多孔空心砌块模型相比，实心砌块模型的内侧瞬态热流对外侧温度非稳态变化更为敏感，其内侧瞬态热流曲线呈正弦变化且峰值更高、谷值更低，多孔空心砌块模型则相对较为稳定且存在一定的时间滞后.由图6(b)可见，实心砌块模型的整体温度上升较快，高于多孔空心砌块模型.在墙材的稳态热阻设置相同时，多孔空心砌块模型在非稳态外侧环境下的瞬态热流和瞬态温度变化比实心砌块模型的离散度更小，变化更为稳定，保温性能更好.

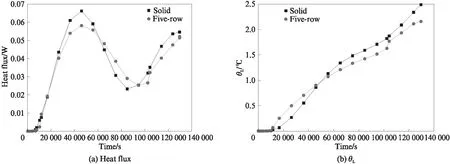
图6 非稳态环境对实心砌块与空心砌块模型传热的影响Fig.6 Effect of unsteady environment on heat transfer of solid block and hollow block

3 受力特征分析

除了满足热学要求，以上设计的多排孔砌块模型也应满足力学性能要求.多排孔砌块模型的孔洞率很大，而且自重较轻，多用于非承重墙.非承重墙同时也是承重墙的重要支撑部位，根据GB 50574—2010中表3.2.2-3规定：烧结多孔砌体最低强度等级为MU3.5，用于外墙或潮湿环境下的墙体强度等级须满足大于等于MU5，不可出现明显应力集中.

3.1 加载方式与边界条件

根据GB/T 2542—2003《砌砖墙检验方法》中的三点加载抗折试验设置尺寸参数，在5排孔砌块模型上方(长×宽所在面)正中央加1块宽为15mm的木板，使木板下表面与砌块上表面面面接触以建立绑定约束，然后在木板上施加均布加载力[12]，见图7.边界条件为模型底面上的两侧宽上进行3个方向全约束.

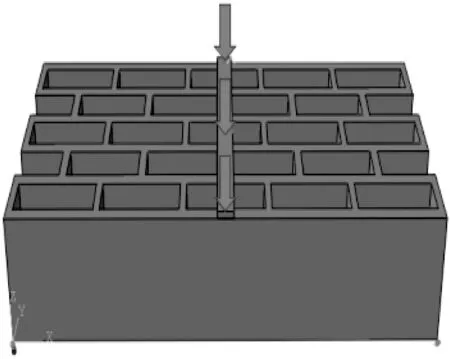
图7 5排孔砌块模型抗折模拟加载部位Fig.7 Loading position of five-row hole’s block

3.2 抗折强度模拟

3.2.1抗折强度受横壁厚的影响

图8为横壁厚为10mm的5排孔砌块模型S11(指空心砌块的400mm长度方向，下同)应力云图.在5排孔砌块模型正中央选择1个特征点(图8深色圈所示位置).固定5排孔砌块模型孔洞率63.75%，当横壁厚由0mm增至14mm(此时竖肋宽约 0mm)变化时，特征点的S11拉压应力值如 图9 所示.其中，横壁厚为0mm和竖肋宽为0mm的实际模型并不成立，且壁厚在6mm以下时极易折断，应力集中现象显著，因此在作拉压应力-横壁厚变化曲线图时不予考虑.

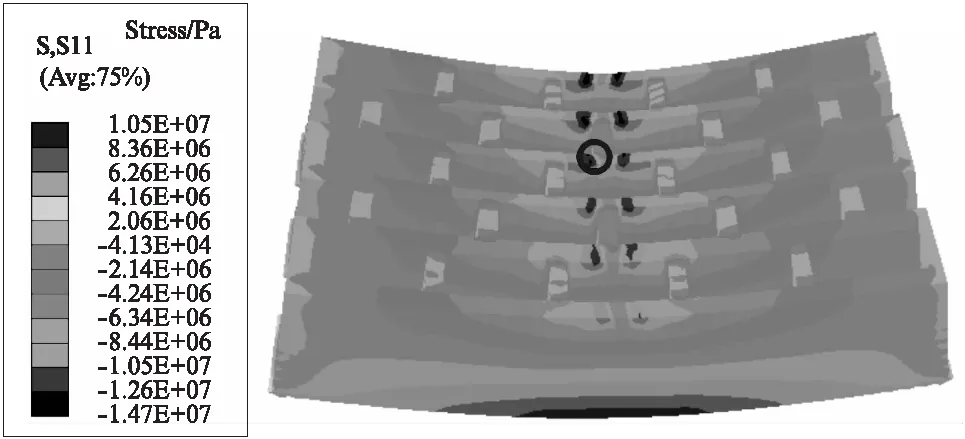
图8 横壁厚为10mm的5排孔砌块模型S11应力云图与 特征点示意图Fig.8 S11 stress cloud diagram with transverse wall thickness of 10mm for five-row hole’s block

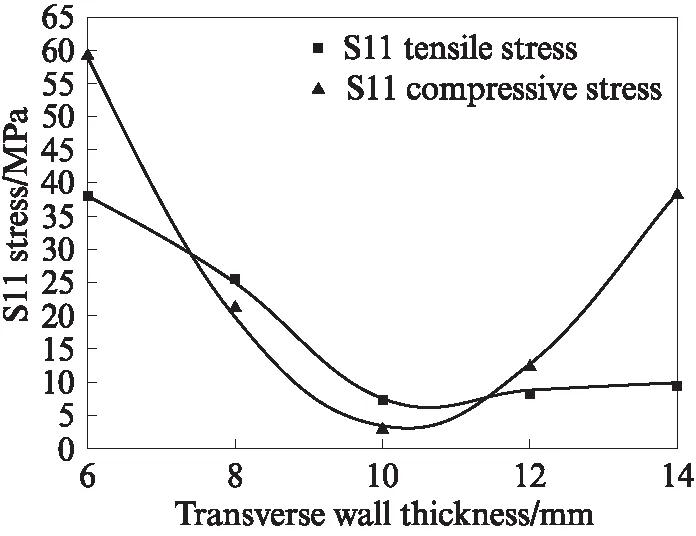
图9 5排孔砌块模型特征点的S11拉压应力值随横壁厚的 变化曲线Fig.9 Change of tensile and compressive stress at characteristic point S11 with transverse wall thickness

当固定5排孔砌块孔洞率为63.75%，横壁厚极端值为6mm或14mm时，5排孔砌块模型中皆发生了应力集中现象，如图10所示.分析模拟结果可知，在横壁厚为10mm时，整个模型最理想，此时受力最均匀，特征点的最大拉压应力也最小.

3.2.2抗折强度受排孔数的影响

固定孔洞率为63.75%，横壁厚为10mm，不同排孔数砌块模型的应力云图特征点皆于其正中央处取得，比如5排孔砌块模型的特征点仍如图8.1～5排孔砌块最优模型的特征点S11拉压应力变化趋势见图11.

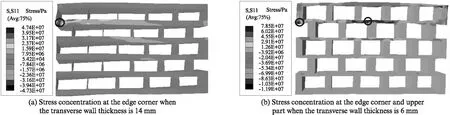
图10 横壁厚为14，6mm的5排孔砌块模型应力集中现象Fig.10 Stress concentration phenomenon of 14 mm and 6 mm with transverse wall thickness

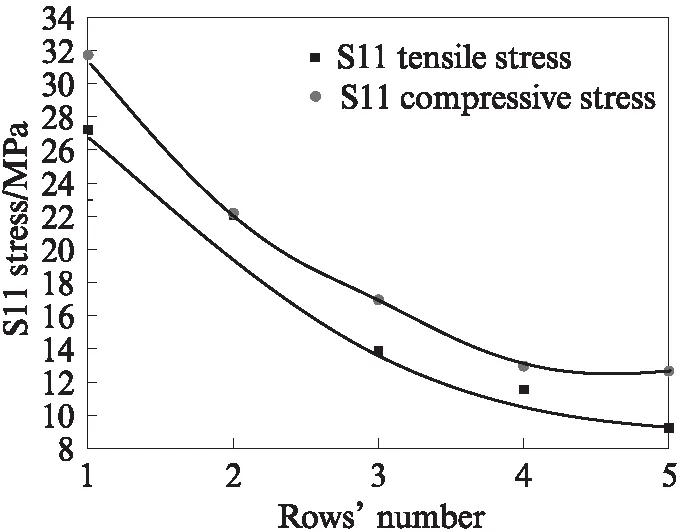
图11 模型特征点的S11拉压应力值随排孔数的变化曲线Fig.11 Change of tensile and compressive stress at characteristic point S11 with rows’ number

由图11可知：(1)模型特征点的S11最大拉压应力都与排孔数呈负相关关系，随着排孔数增加，S11拉应力从27.27MPa降至9.22MPa，压应力从 31.77MPa 降至12.67MPa，且压应力都略大于拉应力；(2)从抗折强度而言，排孔数增加到5排孔时，S11最大拉压应力变化受排孔数的影响已几乎可以忽略，而且，从加工工艺而言，保持60%以上的孔洞率和一定的横壁厚度，砌块排孔数无法做到5排以上.

因此，从力学角度看，最好的孔型设计亦为5排孔.

4 结论

(1)数值模拟解与实测值、规范公式解析值都较为接近，故数值模拟计算稳态墙体传热系数是可行有效的.

(2)稳态环境条件下，孔洞率保持在60%左右时，随着排孔数的增加，砌块模型传热系数明显减小.固定排孔数和孔洞率为63.75%时，随着横壁面积与壁肋面积之比逐渐增加，通过壁肋热流减少，而砌块模型的传热系数与通过壁肋热流呈正相关关系.

(3)非稳态环境(周期性非稳态)条件下，随着排孔数增加，模型内侧瞬态热流和瞬态温度受其外侧传热影响减小，保温性能变好.在墙材的稳态热阻设置相同时，多孔空心砌块模型在非稳态外侧环境下的瞬态热流和瞬态温度变化比实心砌块模型的离散度更小，变化更稳定，保温性能更好.

(4)砌块模型的最大拉压应力与排孔数呈负相关关系，即其随着排孔数增加而减小.当排孔数增加到5排孔时，砌块受弯折时的最大拉压应力变化受排孔数的影响已几乎可忽略.综合考虑加工工艺，设计的厚240mm、5排孔砌块兼顾了热力学性质与施工工艺，为最优孔型设计.