时间尺度上二阶拟线性阻尼动力方程的振动性分析

李继猛，杨甲山

（1.邵阳学院 理学院,湖南 邵阳422004；2.梧州学院 大数据与软件工程学院,广西 梧州543002）

0 引言

研究时间尺度上二阶拟线性变时滞阻尼动力方程[1]的振动性。假设:

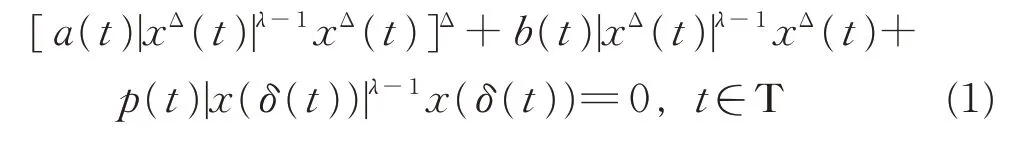
(H1)λ>0为实常数;T为任意时间尺度，且supT=∞。

(H2)δ:T →T是严格递增且可微的时滞函数，满足

(H3)函数a,b,p∈Crd(T,(0,∞))，即其均为已知的正的实值rd-连续函数，且-b/a∈ℜ+。

方程(1)的解及其振动性的定义可参见文献 [1-4]。设t0∈T 且t0>0,则[t0,∞)T为时间尺度区间，其定义为[t0,∞)T=[t0,∞)∩T。近年来，有关时间尺度上一阶及二阶动力方程振动性的讨论有很多[1-18]，文献[1-2，4-5]分别在正则情形和非正则情形下，即在条件

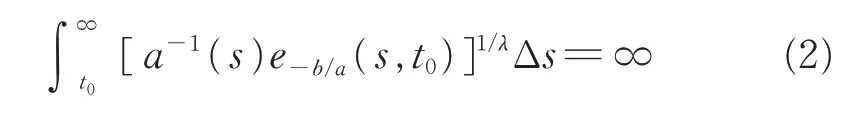
和

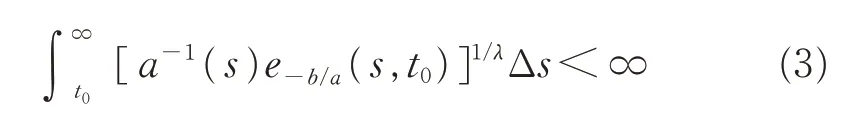
下研究了方程(1)的振动性，并得到了该方程的一系列振动准则。主要结论有:

定理A[1]设(H1)～(H3)及式(2)成立，如果φ∈C1(T,(0,+∞))，使得

则式(1)在[t0,∞)T上振动。

定理A 就是文献[1]中的定理4.1，由此定理及其证明就能得到方程(1)的Kamenev 型振动准则[1](文献[1]的定理4.2)和各种Philos 型振动准则[2,4-5]。

定理B[1]设(H1)～(H3)及式(3)成立，且

若φ∈C1(T,(0,+∞))使得式(4)成立，则在[t0,∞)T上式(1)的每一个解x(t)或者振动或者收敛于0。

定理B 就是文献[1]中的定理4.3。显然,在方程是非正则情形下，定理B 只能确定其每一个解x(t)或者振动或者渐近于0。由于此结果是不确定的，在应用时很不方便，文献[2]中的定理4.3、定理4.4及文献[9]中的相应定理也如此。之后，文献[4-5]对上述结论进行了改进，得到

定理C[4]设(H1)～(H3)及式(3)成立，且

其中t1≥t0足够大，函数如果φ∈C1(T,(0,+∞))使得式(4)也成立，则式(1)在[t0,∞)T上振动。

定理C 就是文献[4]中的定理4.3，由此定理的证明思路及条件(6)就可导出方程(1)在非正则情形下其他类型的振动准则[4-5]。注意到，对于非正则情形的Euler(欧拉)方程

基于以上研究，本文将利用广义黎卡提变换、时间尺度的有关理论及不等式技巧，在方程(1)为非正则情形下建立其振动的一些新充分条件，以推广、改进和丰富已有的结果。

1 主要定理和证明

引理1[6]设x(t)是Δ-可微的且最终为正或最终为负，则

引理2[7]设a>0，b>0，γ>0，则

为了叙述方便，记D0={(t,s):t>s≥t0,t,s∈T }，D={(t,s):t≥s≥t0,t,s∈T }，若 函数H(t,s)∈Crd(D,R)，并且满足条件：

(i)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0，

(ii)H(t,s)在D0上对s有连续且非正的偏导数，即HΔs(t,s)∈Crd且HΔs(t,s)≤0，则称H(t,s)属于集合Ω，并记为H∈Ω。

定理1设条件(H1)～(H3)和式(3)成立，并且φ∈C1(T,(0,+∞))使得式(4)成立。进一步，如果H∈Ω，使得

其中常数T≥t0足够大，函数

则方程(1)在[t0,∞)T上是振动的。

证明反证法。不失一般性，可设方程(1)在[t0,∞)T上有一个最终正解x(t)，则t1∈[t0,∞)T，使得x(t)>0 及x(δ(t))>0(t∈[t1,∞)T)。由 方 程(1)，当t∈[t1,∞)T时，有

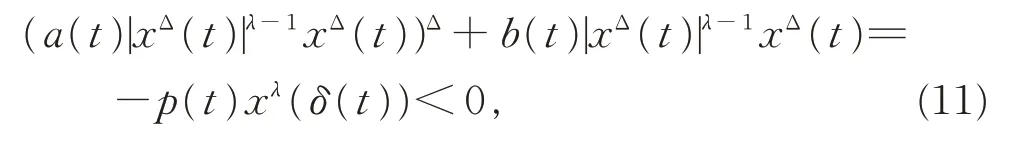
(i)xΔ(t)>0,t∈[t1,∞)T；

(ii)xΔ(t)<0,t∈[t1,∞)T。

情形(i)xΔ(t)>0，t∈[t1,∞)T。同文献[1]中定理4.1的证明，得到与条件(4)矛盾的结论。

情形(ii)xΔ(t)<0，t∈[t1,∞)T。引入 广 义的Riccati 变换

显然w(t)<0(t∈[t1,∞)T)。由于

单调递减，故当s∈[t,∞)T时，就有

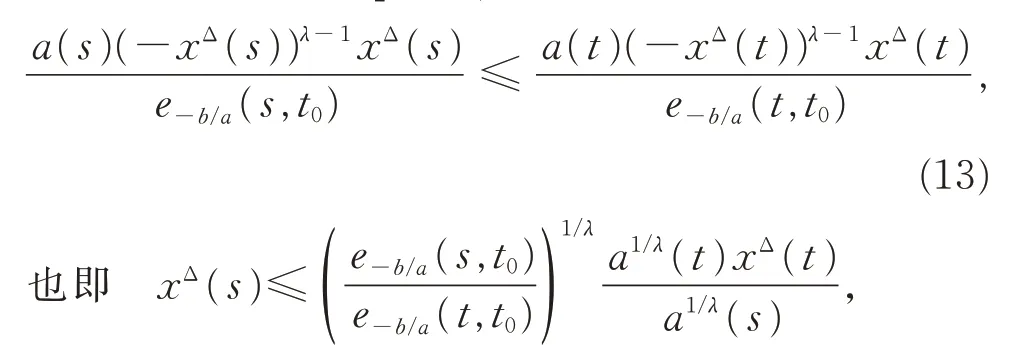
进一步，有

在上式中，令u→∞，得

注意到xΔ(t)<0，由式(8)，容易推得

当0<λ<1时，由式(12)，并分别注意到式(15)、(11)及xΔ(t)<0，可推得

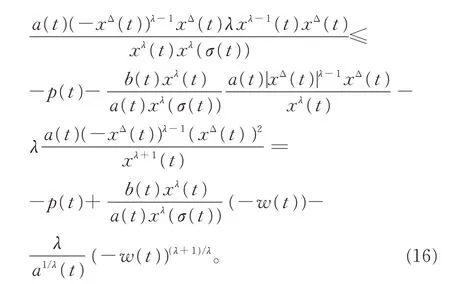
当λ≥1时，注意到式(15)及xΔ(t)<0，同样可得式(16)。

利用式(14)及AΔ(t)=-[a-1(t)e-b/a(t,t0)]1/λ，可得

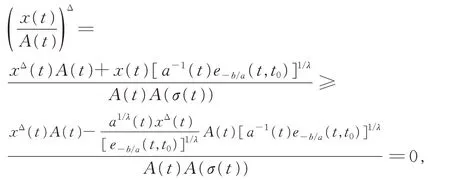
将式(17)代入式(16)，得

现将式(18)两边同乘以H(t,σ(s))后再积分，利用时间尺度上的分部积分公式，即

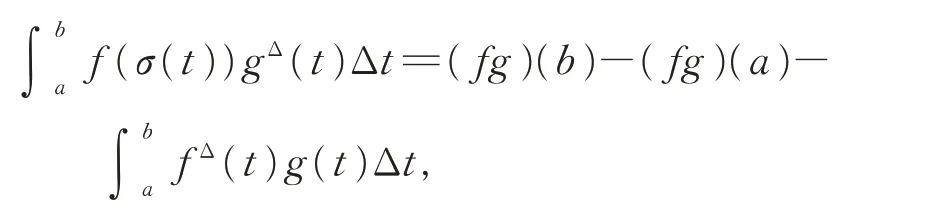
再由引理2，则有

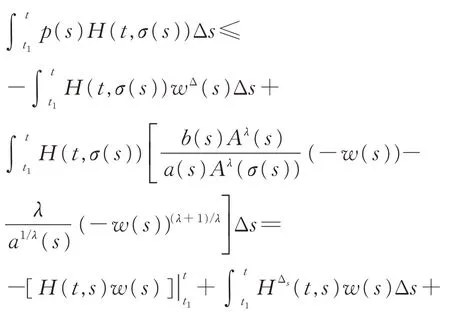
整理得

这与条件(10)矛盾。定理证毕。

注1显然，定理1 是一个新型的Philos 型振动准则，用它来判断方程(1)的振动性所得的结果是确定的，应用非常方便。此外，若令H(t,s)=(t-s)m，则能得到另一新型的Kamenev 型振动准则。限于篇幅,在此不再赘述。

例1考虑二阶Euler 微分方程:

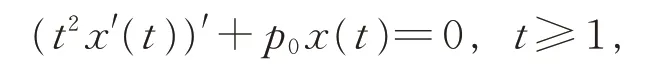
其中常数p0>0。这相当于方程(1)中的a(t)=t2，b(t)≡0，p(t)=p0，δ(t)=t，λ=1，容易验证，条件(H1)~(H3)及式(3)均满足。注意到T=R，则

取φ(t)=1，则

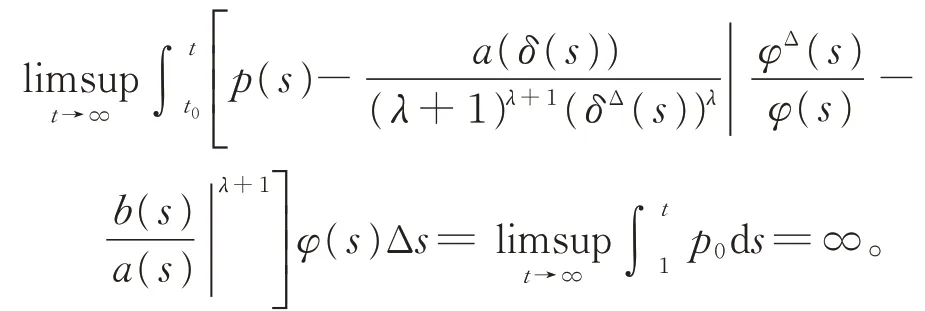
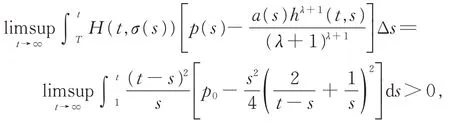
最后一个不等号可参见文献[15]。因此,定理1的条件全部满足，于是当p0>1/4时，方程(7)振动。

注2若用文献[1-2,9]中的定理来判别方程(7)的振动性，则只能得到“方程(7)的每一个解或者振动或者收敛于零”，此结果显然不令人满意。又因为所以文献[4-5]中相应定理的条件不满足，因此，这些文献中的定理对方程(7)也不适用。此外，其他文献，如文献[3,6-8,10-14]中的定理也不适合方程(7)。因此，本文定理推广且改进了已有文献的结果。