径流预报误差的混合t Location-Scale分布模型及应用

孙凤玲，李继清，张验科

(华北电力大学水利与水电工程学院，北京102206)

0 引 言

径流预报误差分析研究主要根据其随机特性进行数理统计分析，包括[1]：一，误差出现的不确定性与统计特性，对误差的不确定度和置信概率给出合理的取值[2-5]；二，径流预报误差的分布，从整体把握预报误差的分布规律。径流预报误差的分布规律研究主要采用单一分布和混合分布模型。目前，大多数文献仍主要集中于建立不同预见期径流预报误差的单一分布模型，单一分布模型在一定条件下呈现出比较满意的效果。Chen等[6]提出了一种基于Copula函数的不确定性演化模型来描述流量预测不确定性的演化规律，生成的预测不确定度序列在均值、标准差和偏度方面与观测序列吻合较好；刁艳芳等[7]发现中国湿润地区、半湿润地区典型水库的洪水预报误差近似服从正态分布；刘招等[8]分别采用正态分布、指数分布、Gamma分布等10余种分布对陕西省安康水库的预报误差进行分析，发现预报误差规律符合Logistic分布；左保河[9]采用实测预报序列误差分析与谱分析相结合的方法研究水文预报中的误差特性，结果发现对数正态分布模型能较好的描述径流预报误差；董前进等[10]研究了三峡水库汛期入库流量预报误差资料，并利用统计图形对三峡水库汛期入库流量预报误差资料进行了Laplace和Logistic的分布拟合，结果发现Laplace分布更适合描述其分布规律。然而，单一分布难以描述不同预见期的径流预报误差的特征多样性。因此，需要建立径流预报误差的混合分布模型，这是具有极大发展潜力的研究方向。王军等[11]将混合分布应用于淮河流域的非一致性水文频率分析；纪昌明等[12]基于高斯混合模型良好的自适应性和高维meta-student t Copula函数的耦合性，建立了径流预报误差的GMM-Copula随机模型，并将模型应用于雅砻江流域锦屏一级水电站水库。混合分布模型作为多个单一分布模型的凸组合，具有形状灵活、结构简单、物理意义明确、模拟性能好等优点。为此，本文基于tLocation-Scale分布良好的自适应性，建立了径流预报误差的混合tLocation-Scale分布模型，利用k均值聚类法进行模型求解，挖掘数据隐含结构获取良好聚类效果，将模型应用于雅砻江流域官地水库，建立了预见期为6、12、18 h和24 h的区间径流预报误差混合tLocation-Scale分布模型，并与tLocation-Scale分布、Stable分布和混合t-Stable分布模型进行比较；最后，利用马尔科夫蒙特卡洛方法(MCMC)产生随机区间径流预报误差序列，并与原径流预报误差序列进行比较分析，验证模型的可行性与有效性。

1 混合t Location-Scale分布模型

针对单一分布模型对统计样本分布特性依赖性强、分布形态单一[13]，且一旦样本本身的分布特性超出所采用的分布模型的描述范围会对预测结果的精度产生较大的影响的缺陷，尝试建立混合分布模型。混合分布模型[14]，即将多个高斯分布、瑞利分布或泊松分布等单一分布模型进行线性组合，使其权重之和为1。混合分布模型提供了一种用简单结构模拟复杂密度的有效方法，是一个分析复杂现象灵活而强有力的工具，广泛应用于聚类分析问题[15]。结合tLocation-Scale分布良好的自适应性，本文构建了混合tLocation-Scale分布模型，主要包括模型的建立、求解、评价和应用方法四个方面内容，模型框架图见图1。

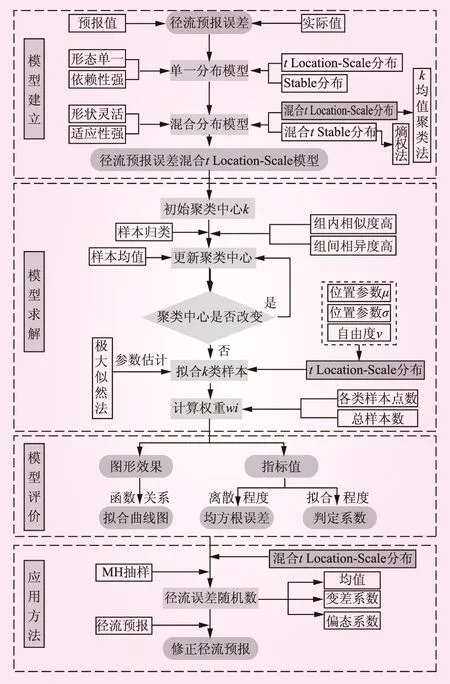
图1 径流预报误差混合t Location-Scale分布模型框架

1.1 模型建立

tLocation-Scale分布是含有位置参数和尺度参数的t分布，即若X～tLocation-Scale(μ，σ，ν)，则(X-μ)/σ～t(ν)。其中，μ为位置参数；σ为尺度参数；ν为自由度。tLocation-Scale分布的概率密度函数为

(1)

单一tLocation-Scale分布模型常常用于描述呈正态分布的小样本数据，当样本数据较大或呈偏态分布时，tLocation-Scale分布模型的拟合效果将会大大降低；不同预见期的径流预报误差序列，tLocation-Scale分布模型的拟合效果差异较大。径流预报误差单一分布模型只能描述特定分布形态的径流预报误差，且随着预见期的不同，径流预报误差分布形态各不相同，拟合效果差异较大。混合tLocation-Scale分布模型较单一tLocation-Scale分布模型在结构上相对复杂些，但混合tLocation-Scale分布模型具有灵活、适用性强等优点。因此，适宜建立径流预报误差混合tLocation-Scale分布模型。

在滚动预报方式下，设xs(j)，t(i)为在作业预报时刻s(j)(1≤j≤N)预报未来时刻t(i)(1≤i≤n)来流所产生的误差，采用相对误差的形式表示径流预报误差，建立径流预报误差混合tLocation-Scale分布模型的概率密度函数。即

(2)

(3)

式中，q′s(j),t(i)、qs(j),t(i)分别为第t(i)时刻的预报径流和实测径流；wk为第k个tLocation-Scale分布权重；p[xs(j)t(i);μk，σk，νk]为第k个tLocation-Scale分布的概率密度函数。

1.2 模型求解

模型求解主要是对混合分布的各参数进行估计，包括权重系数估计和概率密度函数估计，权重系数的估计主要采用聚类分析方法。聚类分析是数据挖掘技术的组成部分，k均值聚类是最著名的划分聚类算法，具有挖掘数据结构隐含结构，简便易实现、效率高，计算速度快等优点，可以对多种数据进行聚类。k均值聚类基于距离相似度判定，在给定k的条件下找到使组内误差平方和最小的划分界，以达到组内相似度高，组间相异度高。k均值聚类的算法过程如下：

(1)从n个样本中选取k个作为初始聚类中心。

(2)对于剩下的样本点，根据其与样本中心的距离，分别分配给相应类中心所在的类别。

(3)计算每个类别新的聚类中心。

(4)不断重复步骤(2)、(3)，直到聚类中心或所有样本点的分类不再改变为止。

通过k均值聚类法确定k个聚类样本后，采用tLocation-Scale分布分别拟合k类样本，进而采用极大似然法估计相应的参数[14]，k类样本中样本数占总样本的比重即为混合分布中的权重，可求解径流预报误差的混合tLocation-Scale分布模型。

1.3 模型评价

误差分布模型评价主要进行拟合优度的统计假设检验，检验观测数据与依据某一假设或分布模型计算得到的理论数据之间的一致性[16]。径流预报误差分布模型的拟合优度检验常常采用均方根误差和判定系数进行评价[12，17]。均方根误差εRMSE是反映真实值与预报值之间的偏差的函数。判定系数ηCOD是表示回归平方和占总离差平方和的比例[18]，即分布模型对因变量的解释程度，其值的范围为0-1。当均方根误差越小，判定系数越大时，模型性能越好。均方根误差、判定系数的计算公式分别为

(4)

(5)

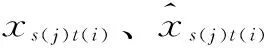
1.4 模型应用方法

基于建立的混合tLocation-Scale分布模型，采用马尔科夫蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法产生随机数，进而模拟一系列的径流预报误差。其基本思路是首先建立一个马尔科夫链，使目标分布为其平稳分布，得到一系列的样本作为来自目标分布的样本，马尔科夫链运行比较稳定时的目标分布与平稳分布比较接近。MCMC方法的抽样方法[19]主要有Metropolis Hasting(MH)抽样法和吉布斯(Gibbs)抽样法。本文采用MH抽样法[20]，主要步骤为：①输入任意选定的马尔科夫链状态转移矩阵Q，平稳分布π(x)，需要的样本个数n。②从任意简单概率分布采样得到初始状态值x0，此时t=0。③从条件概率分布Q(x|xt)中采样得到x*。④计算MH比率R(xt，x*)=π(x*)Q(x*，xt)/π(xt)Q(xt，x*)，进而计算接受概率α(xt，x*)=min{R(xt，x*)，1}。⑤产生随机数u～U(0，1)，抽取xt+1=x*，u≤α(xt，x*)；xt，u>α(xt，x*)。⑥令t=t+1；返回步骤③。

产生径流预报误差随机数后，模拟误差序列为X{xs(j)t(i)}，对径流预报进行修正，得到修正后的径流预报序列Q″{q″s(j)t(i)}，其修正公式为

q″s(j)，t(i)=q′s(j)t(i)/(1+xs(j)t(i))

(6)

2 实例应用

本文选取官地水库2013年1月～2014年6月的区间径流预报误差分析官地水库的径流预报误差特性，分别建立预见期为6、12、18 h和24 h的官地水库区间径流预报误差分布模型。官地水电站坝址位于四川省凉山彝族自治州西昌市、盐源县的交界处，是锦屏一级水电站的又一补偿电站，是雅砻江水电基地的“锦官电源组”5个梯级电站之一，主要向川渝和华东供电[21-22]。官地水库的位置见图2。官地水库的入库径流主要包括2部分：一，来自上游锦屏水库的出库流量；二，上游支流九龙河的区间径流。而不确定性主要是由于上游支流九龙河的影响；因此，研究官地水库的区间径流预报误差特性能有效提高“锦官电源组”梯级水电站的稳定性。

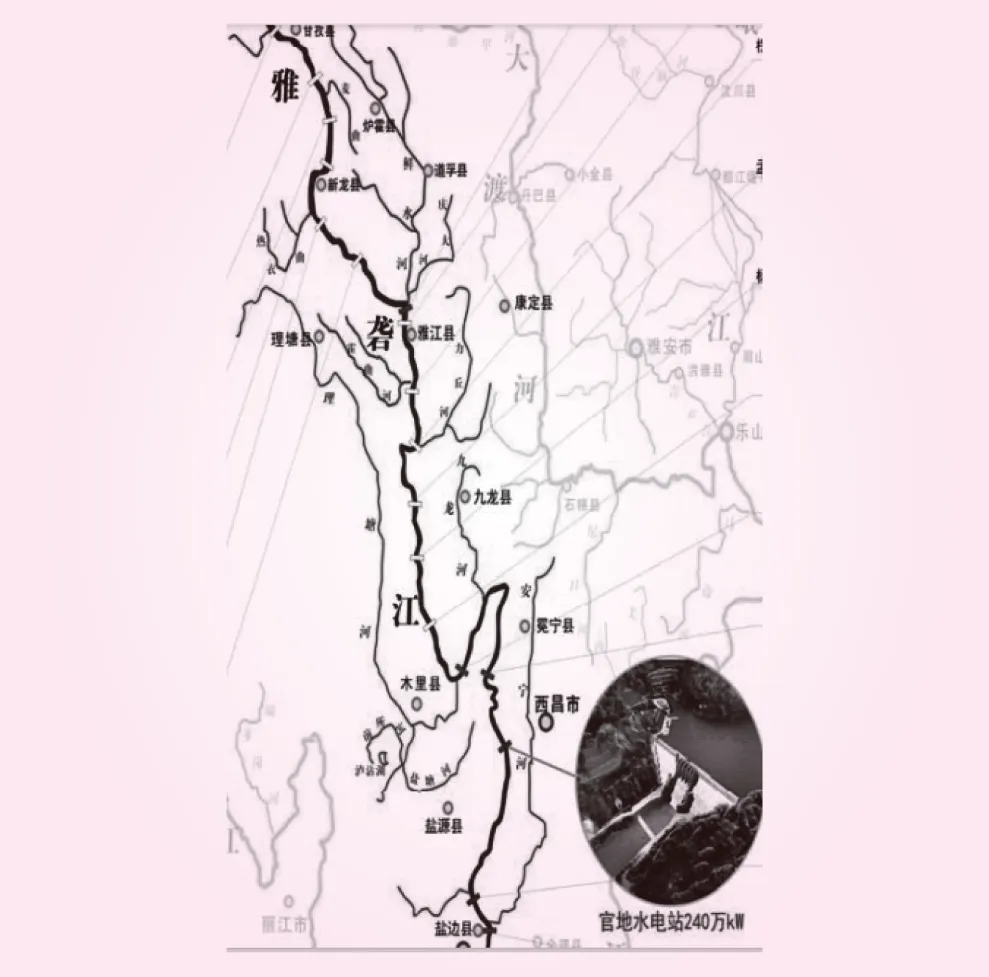
图2 官地水库位置

2.1 建立不同预见期径流预报误差混合t Location-Scale分布模型

针对官地水库不同预见期的区间径流预报误差，应用式(3)建立混合tLocation-Scale分布模型，并将tLocation-Scale分布、Stable分布、混合t-Stable分布作为比较模型。稳定(Stable)分布是一类无穷可分分布，其特征函数一般由4个参数唯一确定[23]。混合t-Stable分布模型是tLocation-Scale分布和Stable分布线性组合的混合分布，其权重由熵权法确定。各分布模型的统计参数估计值见表1。

表1 区间径流预报误差分布参数估计值

2.2 径流预报误差混合t Location-Scale分布模型适用性检验

应用式(4)、(5)分别计算不同预见期径流预报误差各分布模型的均方根误差εRMSE、判定系数ηCOD。不同预见期区间径流预报误差拟合曲线见图3。

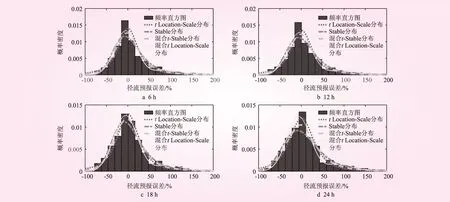
图3 区间径流预报误差拟合曲线

由图3可知，不同的预见期，径流预报误差序列均具有厚尾的特征，正误差厚尾特征更加明显。tLocation-Scale分布、Stable分布、混合t-Stable分布和混合tLocation-Scale分布对区间径流预报误差的峰部、尾部特征描述效果均较好。但仔细观察发现，对于不同的预见期，混合tLocation-Scale分布能更好地描述径流预报误差的尾部特征，特别是正误差的尾部特征与误差分布直方图的拟合效果较好。

不同预见期tLocation-Scale分布、Stable分布、混合t-Stable分布和混合tLocation-Scale分布的均方根误差与判定系数拟合指标值见表2。

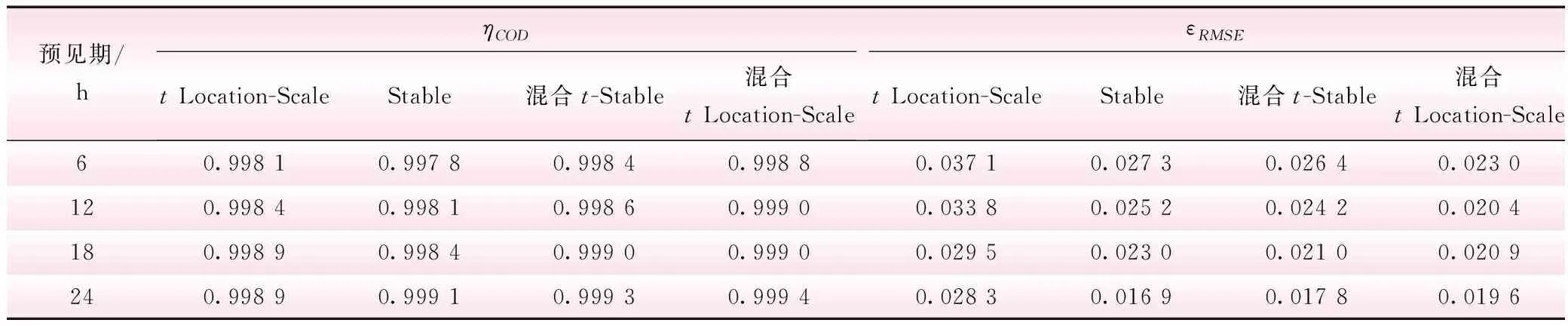
表2 区间径流预报误差拟合指标值

由表2可知，对于不同的预见期，官地水库区间径流预报误差tLocation-Scale分布、Stable分布、混合t-Stable分布和混合tLocation-Scale分布模型的判定系数均在0.99以上，且混合tLocation-Scale分布模型的判定系数均明显高于单一分布模型、混合t-Stable分布模型；同时，比较不同预见期的均方根误差，发现对于预见期为6 h、12 h和18 h的区间径流预报误差分布模型，混合tLocation-Scale分布较tLocation-Scale分布、Stable分布、混合t-Stable分布的均方根误差小；而对于预见期为24h的区间径流预报误差分布模型，均方根误差最小的是Stable分布模型，均方根误差为0.016 9，体现了单一分布模型随着预见期的不同拟合效果差异较大的特点，而混合tLocation-Scale分布模型的均方根误差为0.019 6，分析原因可能是预见期为24 h的区间径流预报误差不确定性较强导致的。结合不同预见期各分布模型的判定系数与均方根误差，不难发现混合tLocation-Scale分布模型描述径流预报误差的效果较单一tLocation-Scale分布、Stable分布和混合t-Stable分布模型好。

对比不同预见期的官地水库区间径流预报误差混合tLocation-Scale分布曲线见图4由此发现不同预见期区间径流预报误差混合tLocation-Scale分布曲线均呈现出“高瘦型”，正误差厚尾特征明显的特征，且随着预见期的增加，区间径流预报误差混合tLocation-Scale分布曲线的形状虽整体上变化不大，但逐渐由“高瘦型”变为“矮胖型”，曲线的最大概率密度值依次为0.013 3、0.012 8、0.012 6和0.012 4；随着预见期的增加，零值附近的概率逐渐减小。这与随着预见期的增加，不确定性增大的规律是一致的。

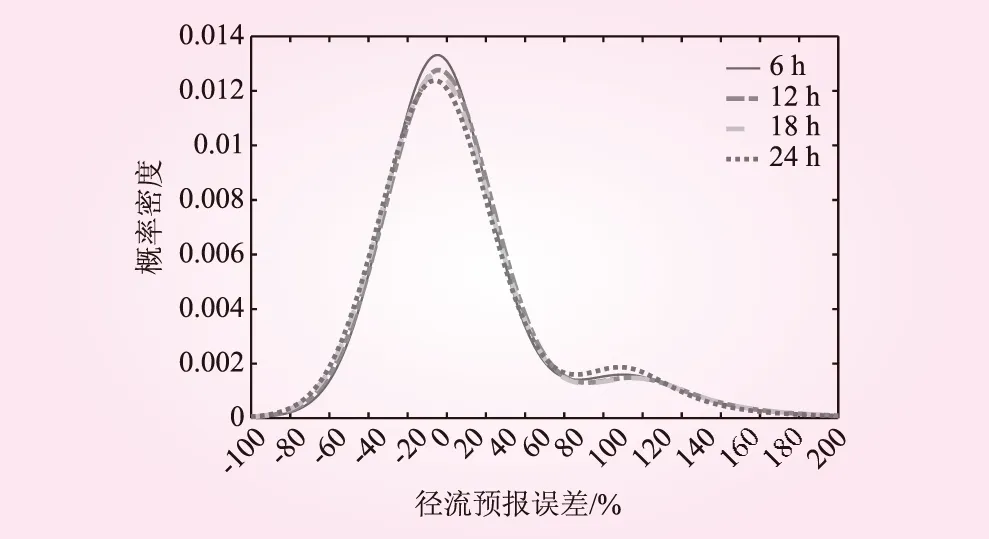
图4 不同预见期区间径流预报误差混合t Location-Scale分布曲线

2.3 径流预报误差混合t Location-Scale分布模型应用

基于建立的径流预报误差混合tLocation-Scale分布模型，利用MCMC方法模拟3 000组区间径流预报误差。计算模拟区间径流预报误差序列与实际区间径流预报误差序列的均值、变差系数、偏态系数等特征值，结果见表3。

表3 模拟误差与实际误差特征值

由表3可知，对于不同的预见期，模拟误差序列与实际误差序列的集中趋势相差不大，均值相对偏差绝对值不超过4%，模拟精度较高；模拟误差序列与实际误差序列的离散程度差异不大，变差系数的相对偏差绝对值不超过13%；模拟误差序列与实际误差序列的偏态系数均大于零，均为正偏，且相对偏差绝对值不超过29%。随着预见期的增加，模拟误差序列与实际误差序列的均值逐渐减小，变差系数逐渐增大，变化规律一致。结合径流预报过程，应用式(6)对预报径流进行修正，便可得到更接近实际来水过程的径流预报过程。

3 结 论

径流预报是水库制订调度方案和实施优化调度的重要理论依据，为提高径流预报的精度，减轻径流预报不确定性的影响，本文建立了描述径流预报误差统计多样性的混合tLocation-Scale分布模型，并将模型应用于官地水库的区间径流预报，主要得出以下结论：①对于不同预见期的官地水库区间径流预报误差，混合tLocation-Scale分布模型较单一tLocation-Scale分布、Stable分布和混合t-Stable分布模型描述径流预报误差的峰部、尾部特征的效果均较好，拟合精度较高；②利用马尔科夫蒙特卡洛(MCMC)方法产生的随机区间径流预报误差序列与实际区间径流预报误差序列各特征值相差不大，且变化规律一致，说明了模型的可行性与有效性。通过叠加模拟的径流预报误差序列与径流预报，可进一步得到比预报来水更接近实际来水的径流过程，为水库水电站的运行管理提供更加丰富的参考信息。本文提出的混合tLocation-Scale分布模型较单一分布模型能更好地描述径流预报误差，还可根据不同分布模型的特性提出不同的混合分布模型描述径流预报误差的统计特性；另外，还可对水库不同时期(汛期、枯水期和过渡期)不同预见期的径流预报误差建立不同的混合分布模型，为水库的径流预报和运行管理提供理论依据。