考虑降雨入渗效应的高边坡开挖数值模拟研究

骆文进，郑晓蕾，王丽英

(重庆建筑工程职业学院土木工程系，重庆400072)

0 引 言

随着我国水利工程的高速发展，对水利工程的边坡设计和施工要求也不断提高[1]。工程上规定坡高大于20 m、小于100 m的边坡为高边坡，其稳定性问题一直是国内外学者重点关注的问题之一[2]。随着高边坡的建设量越来越大，水利工程滑坡事故的数量近年来有所增加，给工程的安全与经济造成巨大危害[3-5]。由于水利工程边坡的地质条件复杂，坡体形式各异，气候差别明显等因素，导致不同地区的边坡产生滑动、崩塌和失稳等工程事故的原因各不相同[4]。因此，针对高边坡的稳定性问题开展研究具有重要的现实意义。

有限元数值模拟分析是研究建筑、道路、地基和边坡等工程建设安全性的一种较为成熟的方法。早在20世纪60年代，就有学者将有限元方法应用于边坡稳定性分析[6]。发展至今，有限元数值模拟法已经成为目前工程界进行边坡稳定性分析的最常用方法之一。有限元数值分析法可以考虑不同边坡岩土体的应力-应变本构关系，理论体系相对严密，也可以通过改变模型的形式和材料参数以模拟不同边坡形状和支护体系的工况，对于边坡变形和渗流的耦合计算有很大优势[7]。

岩土体的水文条件是影响水利工程高边坡长期稳定性的重要因素之一。边坡经过开挖后会形成临空面，使岩土体受降雨入渗影响而引起边坡稳定性下降。当前，国内外学者利用多种数值模拟软件对边坡在降雨入渗工况下进行了稳定性分析。杨龙等[8]采用Geo-slope软件分析了降雨条件下高边坡的实际渗流场，得到了边坡稳定性与降雨量之间的关系，指出降雨影响深度是影响边坡稳定的重要因素；钟佩文等[9]利用FLAC 2D数值模拟软件建立了土质边坡的数值模型，指出降雨入渗作用使土体的强度显著减小，导致塑性区逐渐扩展形成剪切带进而诱发滑坡事故；叶帅华等[10]通过PLAXIS 2D有限元软件对降雨入渗条件对多级黄土高边坡的变形的影响进行了数值模拟，得到了边坡稳定性指标在降雨入渗中的变化规律；刘子振等[11]建立了粘土质临危边坡体三维数值模型，依据极限平衡理论与强度折减法对边坡体在降雨入渗影响下的稳定性进行了评价，并获得了坡体潜在滑动面的位置和形状。

在长期的环境变化影响下，土体力学性质易发生劣化，进而影响高边坡的服役性能。在工程中，忽略降雨入渗的影响往往会引发边坡发生突然性滑塌。因此，本研究针对某水利工程沿线的黄土边坡常年受降雨入渗作用的影响特征，研究降雨入渗深度与设计坡比对高边坡稳定性的影响，采用FLAC 2D数值分析软件对黄土高边坡进行建模，旨在通过数值分析的结果为水利工程高边坡的建设提供参考。

1 边坡稳定性分析方法

目前，工程界常用的边坡稳定性分析方法有极限平衡法和有限元强度折减法[11]。其中，极限平衡法已经在边坡工程中应用了几十年，其适用性已经得到了广泛验证，但也具有一定的局限性。如运用该法不能对岩土体应力-应变关系的差异性进行综合考量，并且该法仅通过几个基本假定直接求解滑动面稳定性安全系数，求解过程缺乏对实际工况的反映，获取的结果精确性较差[12]。

随着有限元理论和应用软件的快速发展，越来越多的学者采用数值模拟分析法评价水利工程高边坡的稳定性。FLAC 2D分析软件作为一种通用的数值模拟软件，能对各类复杂工程问题进行模拟，在边坡工程分析中得到了大量的应用[13]。FLAC 2D分析软件对不同类型的边坡工程有较强的适用性，并可以采用各种编程语言对计算程序进行二次开发，以此克服采用极限平衡法时需预先假设滑移面形状与位置的缺陷。基于FLAC 2D软件的有限元数值模拟能准确地得到边坡开挖过程中的位移场和应力场分布形式，且可以定量地反映边坡体稳定性的变化规律[14]。

本文以某水利工程黄土质高边坡为工程背景，分析降雨入渗深度和设计坡比对边坡稳定性与滑动面的影响。根据有限元单元强度折减法进行边坡稳定性分析的过程见图1。图1中，k1、k2为有限差分法分析中的2个极限值(k2≥k1)；η为给定的误差。在分析过程中，以计算结果的收敛为有限差分法分析结束的判据，在软件中输入抗剪强度参数，即粘聚力c和内摩擦角φ，采用二分法对强度参数进行折减以逼近失稳极限；当计算得到的折减系数ra<10-5时表示计算达到收敛状态；若结果不收敛，则重复上述计算直到折减系数满足收敛要求。本计算采用Fish语言编辑命令流，再导入数值模型进行计算，命令流的下限k1和上限k2取值为0和2。

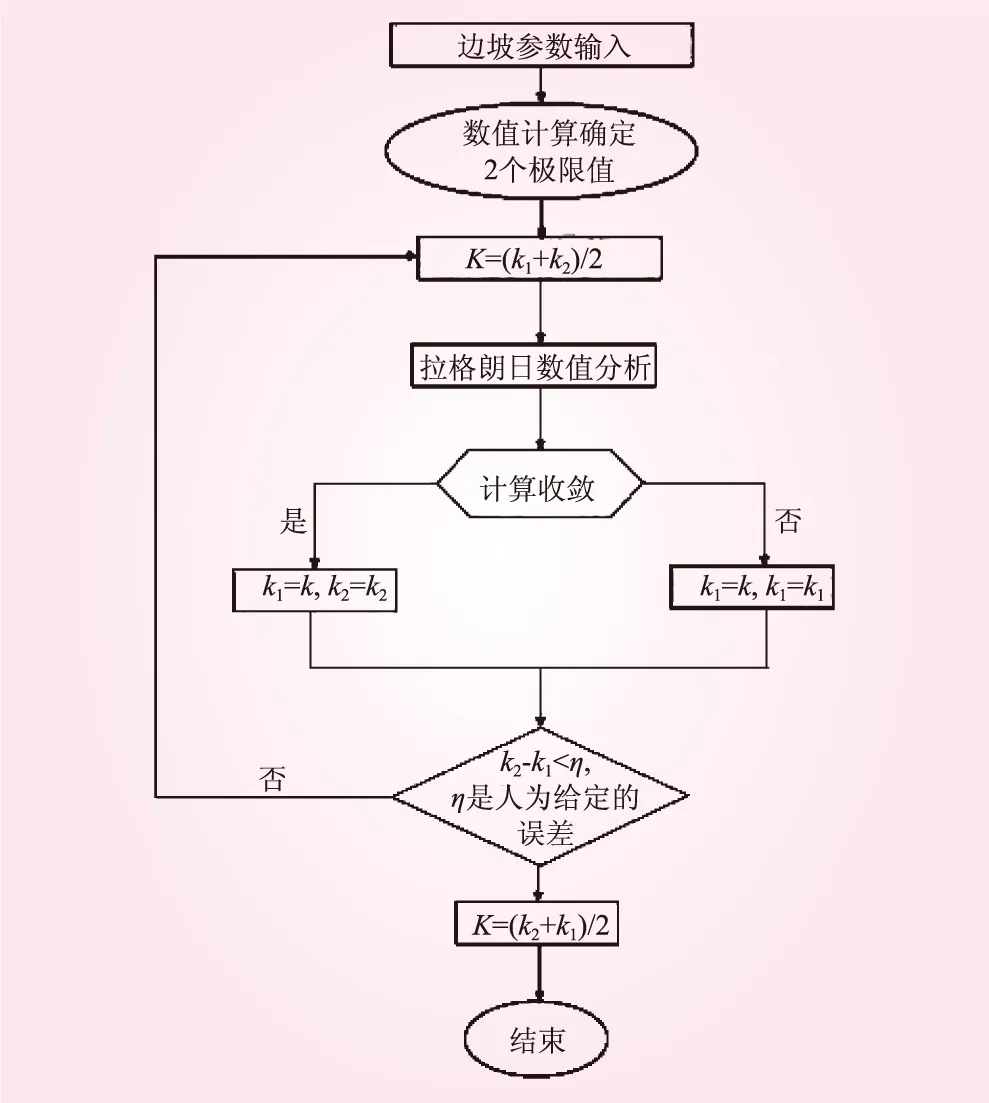
图1 计算流程示意

2 模型建立

2.1 数值模型参数

现场地勘结果表明，边坡自上而下分布粉质黄土、砂土、砂质粘土层和深厚的风化泥岩层。该边坡的坡体延展方向近似为东西向，长约280 m，宽约为64 m，坡体高约22 m。在土工试验室内开展试验，获得了该边坡不同类型岩土体在天然与浸水状态下的物理力学基本参数，具体数值见表1。

表1 模型材料参数

2.2 边坡的有限元模型

参照该水利工程高边坡的设计图，建立了二维边坡的数值模型。为了简化有限元数值模拟计算的过程，在计算模型中对边坡顶端设置自由约束，侧面和底面边界设置位移约束。按照两级放坡模式建模，模型坡高设置为22.0 m，坡前的场地长度设为15.0 m，坡后的场地长度设为22.5 m，平台长度设为5.0 m。利用FLAC 2D软件中的平面应变单元进行边坡模型的网格划分，边坡模型共包含725个节点，5 540个计算单元，建立的模型网格见图2。在数值模拟中，通过改变降雨入渗深度h(1.0～6.0 m)以反映降雨量差异对边坡稳定性的影响；通过改变坡比以反映开挖坡度对边坡稳定性的影响。采用摩尔-库伦的本构关系进行数值计算，基于结果分析不同设计坡比与降雨入渗深度对边坡稳定性的影响规律。

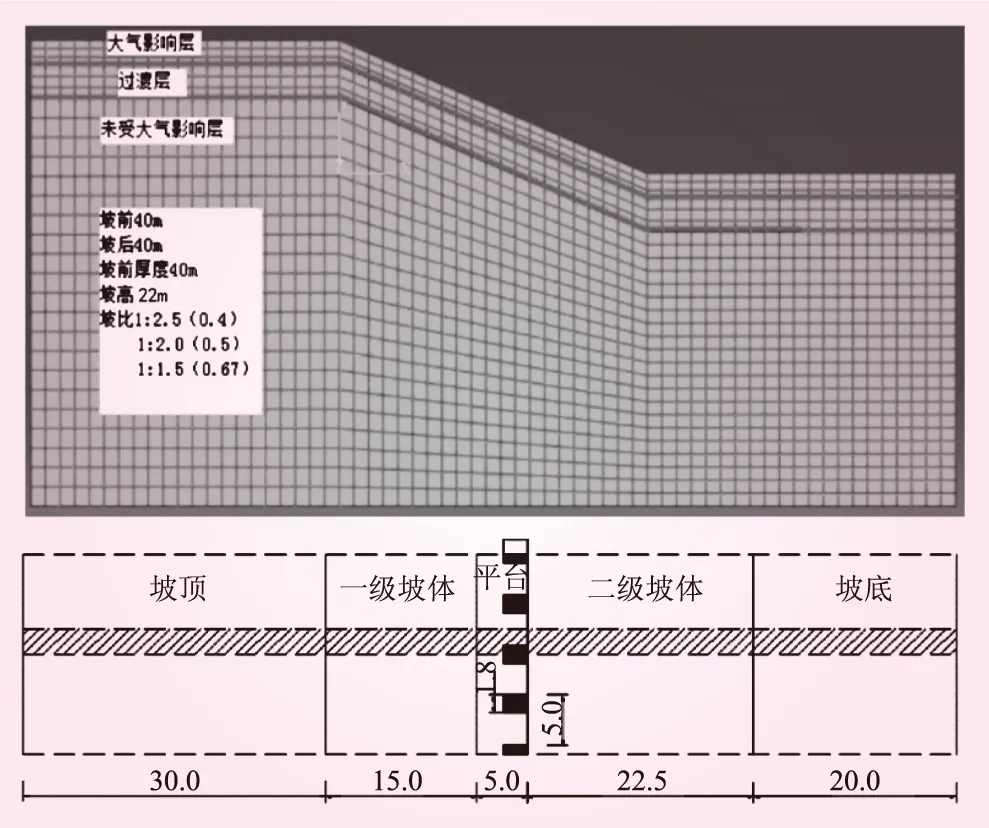
图2 数值模型(单位：m)

3 数值计算结果

3.1 稳定性安全系数Fs

边坡的设计坡比等于边坡的高度与长度之比，坡比值越大代表该边坡越陡峭。本研究通过计算，得到了坡比为1∶1.0、1∶1.5和1∶2.5这3种工况下的边坡稳定安全系数及相应的位移场。同时，为了反映降雨量大小对边坡稳定性影响，采用不同降雨入渗的影响深度(0～6 m)代入数值模拟模型，得到边坡稳定性安全系数结果见表2。

表2 高边坡的稳定性安全系数计算值

为了更清楚地反映边坡的设计坡比对于稳定性安全系数Fs的影响，绘制不同坡比模型安全系数随降雨入渗深度变化关系图，见图3。从图3可知，降雨入渗深度从0到6 m不断增加的过程中，坡比为1∶1.0、1∶1.5和1∶2.5的边坡稳定性安全系数Fs分别下降了15.6%、9.9%和6.7%。可见，设计坡比的增加对边坡的稳定性有明显不利影响。而对于入渗影响深度为0的边坡，在坡比由1∶1.0减小到1∶2.5过程中，Fs从1.651提高至2.280，即边坡稳定性安全系数提高了38.08%。随着降雨入渗深度的增加，Fs逐渐减小。此现象说明降雨量越大，降雨入渗的影响深度越大，则边坡的稳定性就越差。

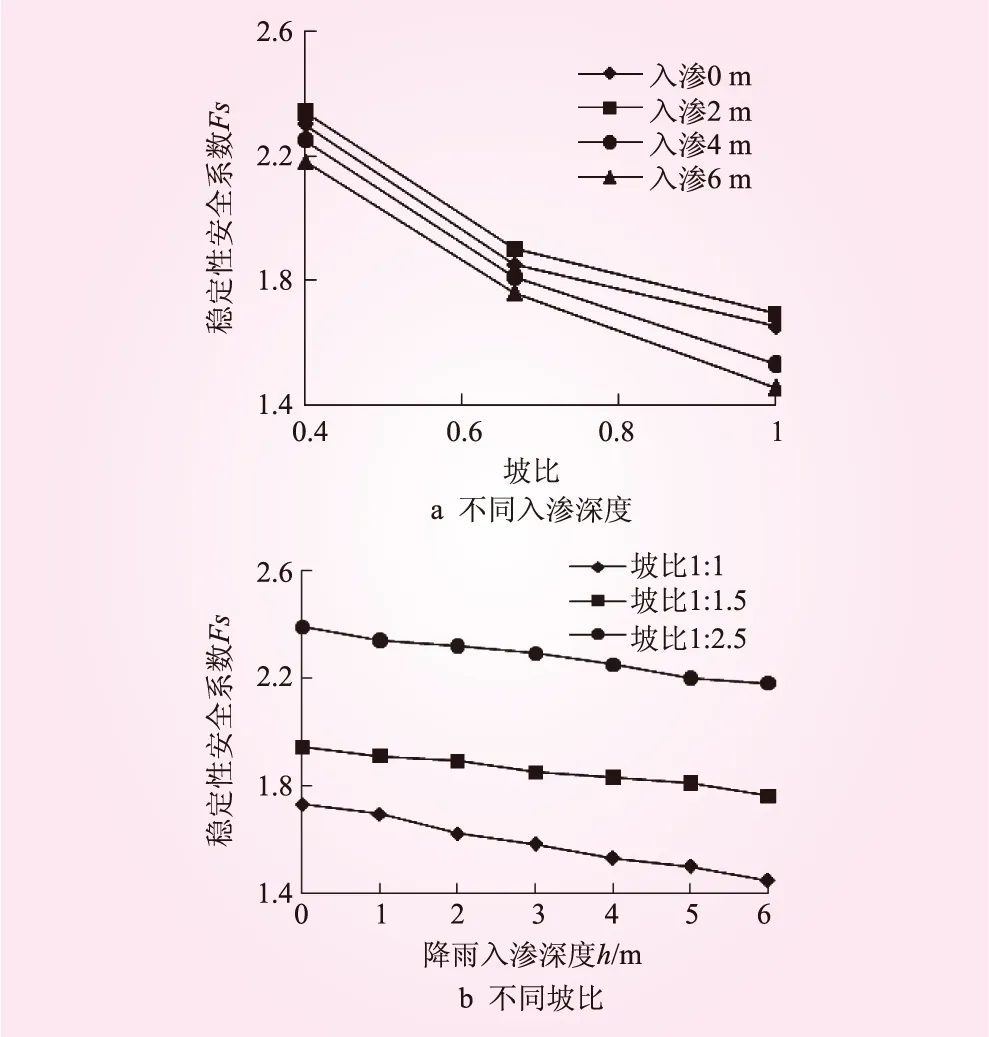
图3 边坡稳定性系数变化

3.2 降雨入渗深度和设计坡比对塑性区分布的影响

不同降雨入渗深度边坡稳定临界塑性区见图4。从图4可知，不同降雨入渗影响深度下边坡的临界状态塑性区分布有如下规律：

图4 不同降雨入渗深度边坡稳定临界塑性区

(1)入渗深度为0时，边坡的塑性区从坡脚刚刚开始形成，潜在滑动面呈类圆弧形状。随着入渗深度从0增加至4 m的过程中，坡脚的塑性区逐渐向上发展并贯通，当入渗深度为4 m时，坡体在入渗锋面处形成狭长的塑性变形区。

(2)入渗深度为5 m时，入渗锋面的塑性区基本连通并通过坡脚形成潜在滑动面；当入渗深度达到6 m时，坡体的潜在滑动面大致形成，此时边坡的稳定安全系数Fs最低。在降雨入渗深度从0发展到6 m时，潜在的滑动面位置从边坡的深部逐渐向浅层坡面发展。

因此，降雨入渗深度对于水利工程高边坡的塑性区分布有着直接影响，降雨入渗深度越大，越容易形成潜在的滑动面，从而诱发坡体的局部和整体滑塌。

以降雨入渗深度为6 m为例，不同设计坡比下的边坡塑性区分布见图5。从图5可以看出，虽然3种工况的塑性区均呈类圆弧形，并通过坡脚，但具体的塑性区形状与位置存在一定差异。在坡比增大过程中，塑性区逐渐由深层向浅层发展，潜在滑动面也逐渐变窄，圆弧滑动面曲率不断减小，形状逐渐细长化。最大位移值也随坡比增加而不断变大，尤其是降雨入渗深度从4 m增加至5 m后，塑性分布区的位移显著增加。

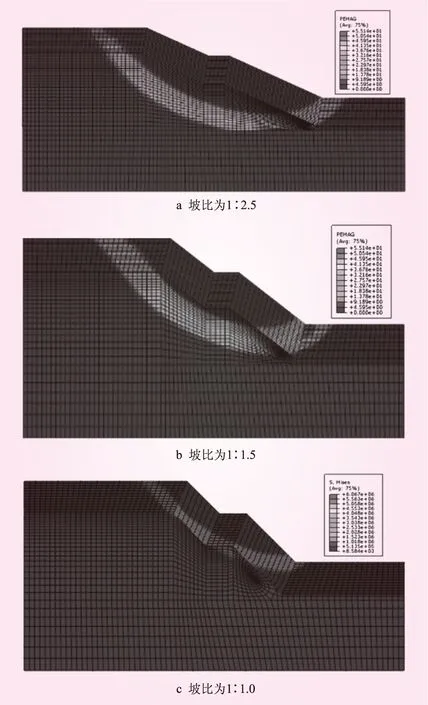
图5 不同坡比边坡稳定临界塑性区

综上，随着降雨量持续增加，边坡的降雨入渗深度也逐渐增加，导致边坡的潜在滑动面由深部向浅层发展，边坡稳定性不断降低。此外，设计坡比也是影响边坡稳定性的重要影响因素，坡比的设计值过大，使得开挖面的塑性分布区位移显著增加。因此，在进行水利工程高边坡的防护和加固时，应切实做好防水、排水的措施，并在重要工程中适当减小设计坡比。对存在安全隐患的水利工程高边坡，更加应针对性采取边坡防护和加固措施，从而有效抑制黄土边坡受到降雨影响而产生滑动变形[15]。

4 结 语

本研究基于FLAC 2D仿真计算软件，对黄土高边坡在降雨入渗和设计坡比影响下的稳定性进行了分析，得到如下结论：

(1)基于FLAC 2D仿真计算软件的边坡稳定性分析对不同工况均具有较好的适用性，随着降雨入渗深度、边坡设计坡比的增加，边坡的稳定性安全系数不断减小。

(2)随着降雨入渗深度的增加，边坡位移场的塑性区不断发展。在入渗深度从0增加到6 m过程中，潜在滑动面的位置逐渐向坡面发展；当入渗深度为6 m时，潜在滑动面基本贯通。

(3)随着设计坡比增加，边坡的整体塑性区形状越来越细长，潜在滑动面的曲率有所减小，潜在滑动面位置逐渐由深部转向浅层发展。

(4)为了提高边坡稳定性，需要切实做好坡面的防、排水措施，并在重要工程中适当减小坡比。