飞行试验中的卷积码性能研究

李凯，闫蓉

（中国飞行试验研究院，陕西 西安710089）

飞行试验是在真实的飞行环境下对试验机、发动机、武器装备、航电系统等进行的试验科目，由于这些系统均未定型，因此，飞行试验也是一项风险性极大、周期较长的系统工程。在飞行试验通信链路中，由于传输媒质的不稳定性及噪声和干扰的不确定性，信号在传输过程中会出现差错。而飞行试验时飞行器与地面基站或其他运动节点通信过程中，飞行器的高机动性和通信环境快速变化的特点使通信性能进一步变差，因此，需要对无线信号采用信道编码技术，以增强数据在信道中传输和抵御各种干扰的能力，提高系统的可靠性。

卷积码是一种性能优越的信道编码，其编码器和解码器都比较易于实现，同时具有较强的纠错能力。在卷积码的编码过程中，对输入信息比特进行分组编码，每个码组的编码输出比特不仅与该分组的信息比特有关，还与前面时刻的其他分组信息比特有关。同样，在卷积码的译码过程中，不仅从当前时刻收到的分组中获取译码信息，还要从前后关联的分组中提取相关信息。正是由于在卷积码的编码过程充分利用了各组的相关性，使得卷积码具有相当好的性能增益，同时，卷积码还具有译码速度快、时延小等优点。由于卷积码具有众多优势，因此适用于飞行试验中上行遥控链路中的信道编码。本文重点对卷积码展开研究，通过计算机仿真分析多种因素对卷积码误比特率性能的影响。

1 基本原理

1.1 卷积码基本概念

数字信号在实际的传输过程中会受到干扰，导致信号码元波形变差，接收端对接收到的码元判决时容易出错。信道中由于乘性干扰引起的码间干扰可以通过均衡的方法纠正，对于加性干扰在合理选择调制强度、调解方法及发送功率等方面的措施后仍不能满足要求的，一般采用差错控制编码。差错控制编码的基本思想是在传输的信息中增加一些监督码，利用监督码元与信息码元之间的约束关系加以校验，以检验和纠正错误。差错控制编码按照对信息码元处理方式的不同可以分为分组码和卷积码。

卷积码的一般结构如图1 所示。

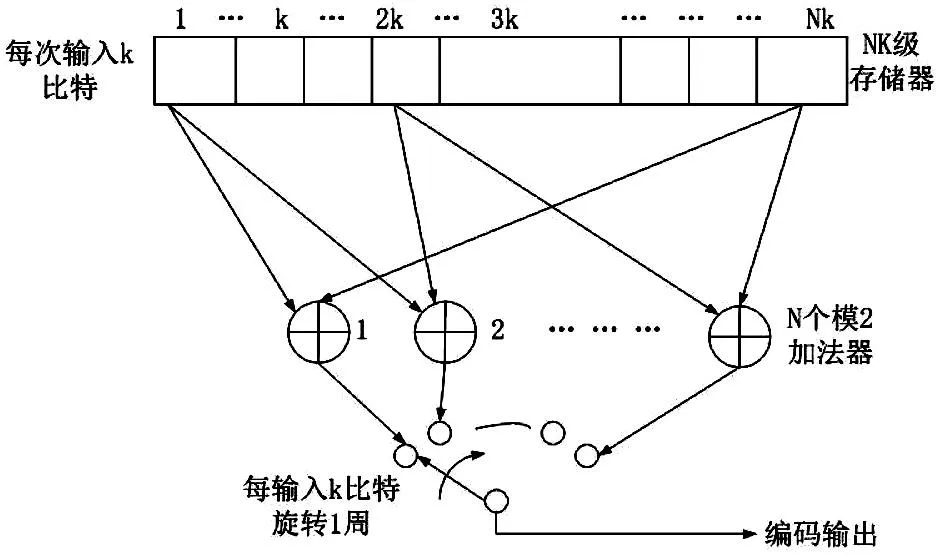
图1 卷积码的一般结构

由图1 可以看出，n 个输出比特不仅与当前的k 个输入信息有关，还与前（N-1）k 个信息有关（N 为约束长度），其性能增益优良、译码速度快、时延小，编码器和解码器都比较易于实现，使用广泛。分组码的实现是将编码信息分组单独进行编码，因此，无论是在编码还是在译码的过程中不同码组之间的码元无关。分组码与卷积码的根本区别在于，它不是把信息序列分组后再进行单独编码，而是由连续输入的信息序列得到连续输出的已编码序列。即进行分组编码时，其本组中的n-k 个校验元仅与本组的k 个信息元有关，而与其他各组信息无关。

同样，在卷积码译码过程中，不仅从此时刻收到的码组中提取译码信息，还要利用之前或之后各时刻收到的码组中提取有关信息。卷积码的纠错能力随约束长度的增加而增强，差错率则随着约束长度增加而呈指数下降。卷积码（n，k，N）主要用来纠正随机错误，它的码元与前后码元有一定的约束关系，编码复杂度可用编码约束长度N*n 来表示。一般情况下，最小距离d 表明了卷积码在连续N 段以内的距离特性，该码可以在N 个连续码流内纠正（d-1）/2 个错误。卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。总之，由于n，k 较小，且利用了各组之间的相关性，在同样的码率和设备的复杂性条件下，无论理论上还是实践上都证明卷积码的性能优于分组码。

1.2 状态图编码

由于卷积码编码器在下一时刻的输出取决于编码器的当前状态和下一时刻的输入，而编码器当前状态取决于编码器当前各种移位寄存器的存储内容。编码器当前各移位寄存器存储内容（0 或1）为编码器在该时刻的状态（此状态代表记忆以前的输入信息）。随着信息序列的不断输入，编码器不断从一个状态转移到另一个状态，并且输出相应的编码序列。编码器的总可能状态数为2mk个。对于（7，5）码的编码器来说，n=2，k=1，N=3，m=2，共有4 个可能状态，其状态如图2 所示。

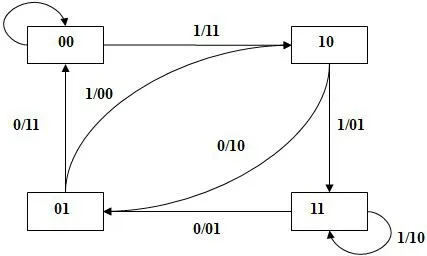
图2 卷积码状态转移图

图2 中4 个方块表示状态，状态间的连线与箭头表示转移方向，连线上的数字表示状态发生转移的到来比特，斜杠后的数字为由一个状态到另一个状态转移时的输出码字，如当前状态为11、输入信息为0，转移到01 状态并输出01 码字，如果输入信息为1，则依然为11 状态，并输出10 码字。

1.3 Viterbi 译码

卷积码概率译码的基本思路为：以接收码流为基础，逐个计算它与其他所有可能出现的、连续的网格图路径的距离，选出其中可能性最高的一条作为译码估值输出。概率最大在大多数场合可解释为距离最小，这种最小距离译码体现的正是最大似然的准则。卷积码的最大似然译码与分组码的最大似然译码在原理上是一样的，但实现方法上略有不同，主要区别在于分组码是孤立地求解单个码组的相似度，而卷积码是求码字序列之间的相似度。基于网格图搜索的译码是实现最大似然判决的重要方法和途径。用网格图描述时，由于路径的汇聚消除了树状图中的多余度，译码过程中只需考虑整个路径集合中那些使似然函数最大的路径。如果在某一点上发现某条路径已不可能获得最大对数似然函数，就放弃这条路径，然后在剩下的“幸存”路径中重新选择路径。这样一直进行到最后第L 级（L 为发送序列的长度）。由于这种方法较早地丢弃了那些不可能的路径，从而减少了译码的工作量，Viterbi 译码正是基于这种想法。

对于（n，k，N）卷积码，其网格图中共2kL种状态。由网格图的前N-1 条连续支路构成的路径互不相交，即最初2k-1 条路径各不相同，当接收到第N 条支路时，每条路径都有2 条支路延伸到第N 级上，而第N 级上的每两条支路又都汇聚在一个节点上。在Viterbi 译码算法中，把汇聚在每个节点上的2 条路径的对数似然函数累加值进行比较，然后把具有较大对数似然函数累加值的路径保存下来，丢弃另一条路径，经挑选后第N 级只留下2N 条“幸存”路径。选出的路径同它们的对数似然函数的累加值将一起被存储起来。由于每个节点引出2 条支路，因此，此后各级中路径的延伸都增大1 倍，但比较它们的似然函数累加值后，丢弃一半，结果留存下来的路径总数保持为常数。由此可见，上述译码过程中的基本操作为“加-比-选”，即每级求出对数似然函数的累加值，然后两两比较后作出选择。有时会出现2条路径的对数似然函数累加值相等的情形，在这种情况下可以任意选择其中一条作为“幸存”路径。

卷积码的编码器从全零状态出发，最后又回到全零状态时所输出的码序列，称为结尾卷积码。因此，当序列发送完毕后，要在网格图的终结处加上N-1 个己知的信息作为结束信息。在结束信息到来时，由于每一状态中只有与已知发送信息相符的那条支路被延伸，因此在每级比较后，幸存路径减少一半。在接收到N-1 个己知信息后，在整个网格图中就只有唯一的一条幸存路径保留下来，这就是译码所得的路径。也就是说，在己知接收到的序列的情况下，这条译码路径和发送序列是最相似的。

2 仿真分析

飞行试验中信号的传输流程如图3 所示，从图3 中可以看出，信号从主数据采集器出来经过编码器进入发射机进行调制，经过发射天线发出无线电波被地面遥测天线接收，经过接收机解调，然后再通过译码器获得高质量的遥测信号。卷积码的使用在其中起到了重要的作用，保障了遥测信号的高效、稳定、无线传输。而卷积码的误比特率性能受约束长度和码率的影响较大，因此，有必要探究约束长度和码率对卷积码误比特率性能的影响。

图3 飞行试验信号传输

卷积码不同约束长度的误比特率性能仿真如图4 所示，参数设置如下。

信道环境：高斯信道环境。

通信体制：基于直扩的外测通信体制。

调制方式：QPSK。

码率：1/2。

约束长度：2，4。

仿真次数：106次。

图4 卷积码不同约束长度下的误比特率性能曲线

卷积码的约束长度是影响其性能的一个重要因素，当改变卷积码的约束长度时，系统的误比特率性能也将随之发生变化，为了研究约束长度对卷积码误码性能的影响，采用码率为1/2 的卷积码为仿真码字，分别使约束长度为2 和4 进行仿真。从图4 可以看出在较高信噪比下，约束长度为4 的卷积码性能较好于约束长度为2 的卷积码性能；在低信噪比下，性能则相反，这是由卷积码的设计造成的。卷积码为了达到较好的性能，判决时不仅要了解本码组的信息，还要了解相邻码组的信息。在低信噪比下，错误的译码会影响其他码组，而且约束长度越长的码组，影响越深。根据以上分析得出：在码率相同时，约束长度越长，系统的误比特率就越低，误比特率性能就越好。

卷积码不同码率的误比特率仿真如图5 所示，为了分析比较码率对卷积码误比特率性能的影响，仿真中使约束长度同为4，卷积码的码率分别采用1/2 和2/3。

卷积码的码率R=k/n，它是卷积码的一个重要参数，当改变卷积码的码率时，系统的误码性能也将随之改变。从图5 可以看出，1/2 码率的卷积码性能要好于2/3 码率的卷积码，原因是码率越小，一帧中冗余量则会更大，在译码阶段可用于判决的信息增加，误比特率性能则更好。因此，可以得出如下结论：在约束长度相同时，码率越低，误比特率性能就越好。

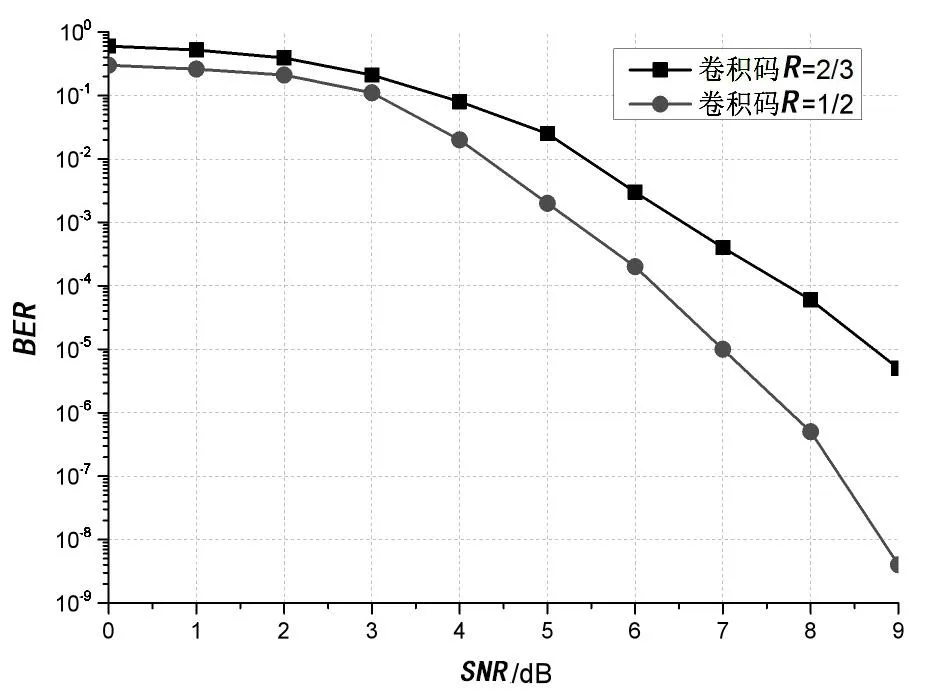
图5 卷积码不同码率下误比特率性能曲线

3 结束语

本文对适用于飞行试验中的卷积码进行了研究分析，分别介绍了卷积码的基本概念、状态图编码原理和Viterbi 译码原理，并通过计算机仿真得出卷积码的误比特率性能曲线。实验得出在码率相同时，约束长度越大，卷积码误比特性能越好，在约束长度相同时，码率越小，误比特率性能越好，为实际工程中卷积码的使用提供了一定的理论参考。