染色问题新解
徐永毅

【摘 要】 染色问题是高考和竞赛中的热点问题,不少同学望而生畏,束手无策。笔者将结合实例,帮大家巧解染色问题。染色问题的解题思路对学生来说非常重要,若能娴熟掌握,类似的数学问题就能举一反三,达到触类旁通的目的。
【关键词】 数学;染色问题;举一反三
求解染色问题,基本思路如下:
第一,将各区域编号;
第二,简化图形,将相邻部分用短线连接;
第三,将不相邻的两个编号写在一起,用颜色种类的多少分析、分类。
“实践是检验真理的唯一标准。”下面提供两道典型例题,对以上三个解题步骤加以具体分析,化繁为简,轻松解决染色问题。
例1:某城市中心广场建造一个花圃,花圃分为6部分(如图1所示)。现在要栽种四种不同颜色的花,每部分栽种一种且相邻部分不能栽种同种颜色的花,不同的栽种方法有多少种?
分析:①将各区域编号,如图2所示;
②化简图形,如图3所示;
③不相邻区域的编号组有(2,4)、(2,5)、(3,5)、(3,6)、(4,6),由于用4种颜色的花栽6个区域,所以要有两个不相邻组(6-4=2)栽同色花,因此要将上述5组重新分组组合(含相同编号的不能分到同一组),即[(2,4),(3,5)]、[(2,4),(3,6)]、[(2,5),(3,6)]、[(2,5),(4,6)]、[(3,5),(4,6)]5组,现从这5组中任选一组,共有种选法,不妨设取出的是[(2,4),(3,5)],此时将6个区域分成(2,4)、(3,5)、(1)、(6)四个区域,用4种颜色的花栽这四个区域有种可能,因此,此题总共有种不同的栽种方法。
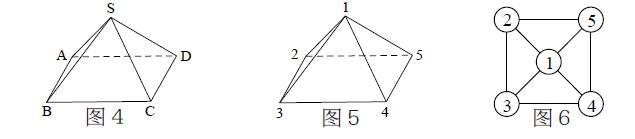
例2:如图4所示,将一个四棱锥每一个顶点染色,并使同一条棱上的两端点异色,并只有5种颜色可供使用,则不同的染色方法总数有多少种?
分析:区域编号、简化图形分别如图5、图6所示。
①当5种颜色全部使用时,有种染法。
②当用4种颜色染色时,只能有一个不相邻组(5-4=1)染同色。而不相邻组有(2,4)、(3,5)兩组,从两组中选一组,有种方法,不妨设取出的是(2,4),此时将5个区域分成(1)、(3)、(5)、(2,4)四个区域,从5种颜色中取出4种颜色,有种方法,用这4种颜色染这四个区域,有种方法,因此,总共有种方法。
③当用3种颜色染色时,必有两个不相邻组(5-3=2)染同色。而不相邻组有(2,4)、(3,5)两组,从两组中任选两组,有种方法,即取出(2,4)、(3,5),此时将5个区域分成(2,4)、(3,5)、(1)三个区域,从5种颜色中取出3种颜色,有种方法,用这3种颜色染这三个区域,有种方法,因此,总共有种方法。
由①②③知,共有++=420(种)染法。
通过对以上两道例题的解析,相信大家对解决染色问题的三个基本步骤有了更深的了解。其实表面上看很复杂、烦琐的问题,往往有“迹”可寻,只要认真思考,掌握染色问题的解题思路,这是解答染色问题的关键。
通过以上两例的分析,相信大家已经掌握了“新”解染色问题的方法,下面提供两道习题操练一下吧!
练习:
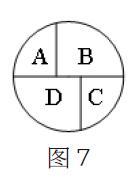
(1)如图7所示,用五种不同颜色分别给A、B、C、D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法有几种?(答案:180种)
(2)如图8所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有多少种?(答案:72种)
怎么样,做起来是不是有种茅塞顿开的感觉呢?其实还是那句古训“世上无难事,只怕有心人”。学习要善于总结和积累,题做得多了,自然熟能生巧,就能悟出“纸上得来终觉浅,绝知此事要躬行”的道理。
笔者为大家提供的染色问题“新”解法,我们亲切地称它为“染色三部曲”,该解法具有很强的普遍性,大多数染色问题都可利用它来解决。通过以上分析解答,相信大家能掌握一些解决染色问题的技巧,通过刷题提高分析推理能力,顺畅解决染色问题。

