基于多匝光纤环的盘式光纤加速度计理论模型

马坤，于天明，杨继勇，年华，李爱秋，杨木森

1.黑龙江省地震局宾县地震台，黑龙江哈尔滨150400

2.哈尔滨工程大学物理与光电工程学院，黑龙江哈尔滨150001

振动传感器种类繁多，加速度计在振动传感器中占有重要的地位并且应用领域广泛[1]，例如：建筑监测、车辆控制、地震预报、油田勘探、航空制导等[2]。传统的加速度计多为机电式加速度计[3]，受限于电子元件的工作特点，机电式加速度计不适合在强电磁干扰或高温的环境中使用。光纤加速度计作为一种新型加速度计，具有灵敏度高、抗电磁干扰、能在较高温度下工作以及易于大规模组网等优点[4-5]，相比传统的机电式加速度计具有更广阔的发展前景。在各种光纤加速度计中，盘式光纤加速度计具有动态范围大、灵敏度高、工作频带宽的优点[6-7]，得到了广泛研究与应用。

盘式光纤加速度计的工作原理是弹性盘受外界振动作用而产生应变，固定在弹性盘表面的传感光纤也会产生应变，采用光学相干原理将光纤应变转换为光学相位变化即可检测外界加速度[8-9]。从1990年被发明出来至今，盘式光纤加速度计吸引了众多研究者的目光，例如通过使用微光纤并且优化光纤环的位置来提升盘式光纤加速度计的性能[10]。盘式光纤加速度计的工作特性比较复杂，包括灵敏度和谐振频率在内的性能参数受到许多因素的共同作用，因此在实用化的过程中必须建立准确的理论模型来指导盘式光纤加速度计的设计与优化。

前人发表过一些基于单匝光纤环的盘式光纤加速度计理论模型，这些理论模型没有体现单匝光纤环对弹性盘的机械性能的影响。自从Geoffrey A.Cranch 等[11]通过多匝光纤环来提高盘式光纤加速度计的灵敏度以来，采用多匝光纤环成为研制盘式光纤加速度计的趋势。然而，光纤环匝数的大幅增加使其对弹性盘的机械性能的影响愈加显著，因而基于单匝光纤环的理论模型不能准确计算出基于多匝光纤环的盘式光纤加速度计的性能参数。

本文采用弹性力学和材料力学的相关理论，建立了基于多匝光纤环的盘式光纤加速度计的理论模型，对灵敏度和谐振频率进行了理论推导；采用有限元仿真软件建立了基于多匝光纤环的盘式光纤加速度计的仿真模型，分析了理论模型和仿真模型之间的误差来源；对研制出的盘式光纤加速度计进行了性能测试，并将测试结果与仿真结果进行了对比。

1 系统结构及理论分析

盘式光纤加速度计是一种弹簧-质量体系，可以将外界的加速度转化为光纤长度变化，进而使光纤干涉仪输出光信号相位差发生改变。

图1是盘式光纤加速度计的工作原理图。基于多匝光纤环的盘式光纤加速度计的拾振结构由弹性盘、质量块、多匝光纤环、封装结构组成。当封装结构受到外界轴向加速度作用时，质量块由于惯性会向弹性盘施加轴向力，使弹性盘发生弯曲并使其上下表面产生等幅反向的应变分布；将作为光纤Michelson 干涉仪两传感臂的2个多匝光纤环分别粘贴于弹性盘上下表面，当弹性盘发生应变时，其上下表面的光纤环受到应变传递作用而分别发生拉伸或压缩，进而干涉仪两臂光信号的相位差变化，导致输出干涉信号强度的改变，最后通过对干涉信号进行探测并解调相位变化信息，实现对外界加速度的测量。由于弹性盘半径远大于厚度，因此对轴向加速度具有很高的响应度。

图1 盘式光纤加速度计传感系统

灵敏度用来衡量加速度计对外界加速度的响应程度，谐振频率决定了加速度计的工作带宽。下面探究基于多匝光纤环的盘式光纤加速度计的灵敏度和谐振频率的理论模型。

多匝光纤环对弹性盘的机械参数的影响不能忽略，例如杨氏模量、泊松比和厚度都发生了变化。下面采用混合材料力学的体积平均法来计算等效机械参数。设弹性盘的外半径为a、内半径为b、厚度为t，在上下表面粘接光纤环后的弹性盘的等效机械参数为

式中：E为杨氏模量；v为泊松比；V为体积。其中下标fc、g、d 分别表示光纤环、将光纤环粘接在弹性盘上的环氧树脂胶、弹性盘。

粘接有光纤环的弹性盘的等效弯曲刚度系数可以表示为

弹性盘外边缘受到封装结构的固定支撑，内边缘被质量块夹紧，发生弯曲的弹性盘的径向转角为[12]

式中：r为弹性盘半径；w是线载荷。设拾振结构所受外界加速度为A，质量块质量为M，w可以表示为

在弹性盘半径为r、轴向高度为z处的环向应变的表达式为

在光纤环高度为z的这一匝光纤的长度变化可以通过对这一匝光纤的环向应变积分得到，表示为

设t1为光纤环与弹性盘之间的粘胶厚度。在匝数为n的多匝光纤环中，第1匝和第n匝光纤的高度分别为

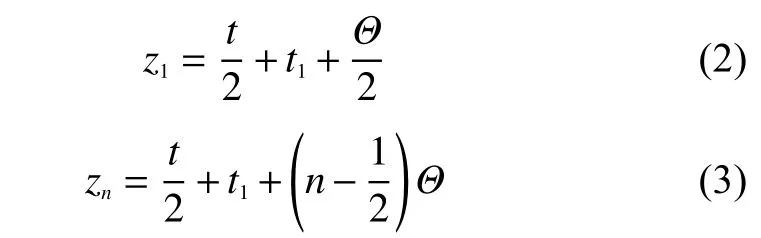
将式(2)、(3)分别代入式(1)中得到第1匝和第n匝光纤的长度变化Δl1和Δln。由式(1)可以看出应变引起的某一匝光纤的长度变化和其所处的高度z成正比，因此，多匝光纤环的光纤长度变化可以表示为

光纤中的相位变化可由光纤长度变化得到：

式中

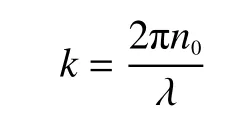
其中：n0为光纤纤芯折射率；λ为干涉仪光源的波长。

由于光纤Michelson 干涉仪的2个传感臂上各有一个光纤环，并且每个光纤环中光信号都经过2次，干涉仪输出的相位差的变化为式(4)的4倍，选择灵敏度的单位为rad/g，加速度计的灵敏度表达式为

盘式光纤加速度计的拾振结构可以等效为受迫振动的弹簧-质量系统，弹簧的刚度由弹性盘和2个多匝光纤环在轴向的刚度共同组成，质量来自质量块。

弹性盘最大挠度在其内半径处，可以表示为

式中：

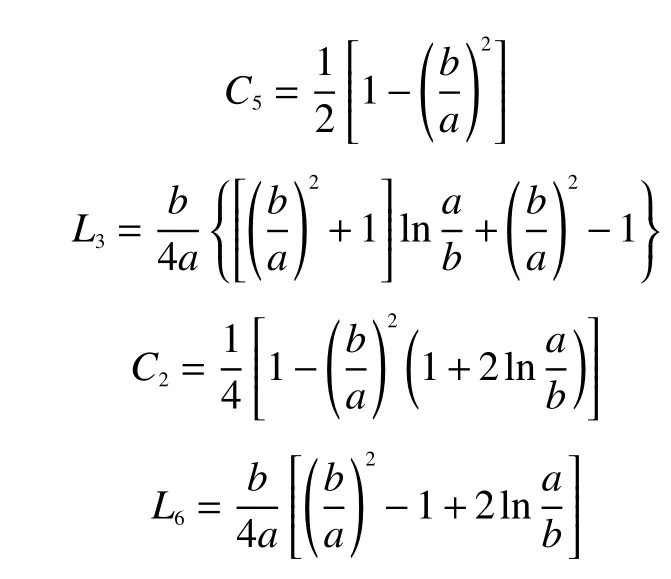
根据广义胡克定律得到粘接多匝光纤环的弹性盘的等效刚度系数为

基于多匝光纤环的盘式光纤加速度计的谐振频率为

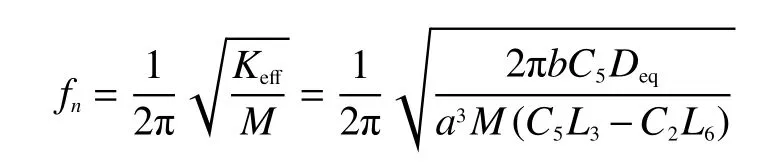
采用表1的参数对基于多匝光纤环的盘式光纤加速度计的性能参数进行理论计算，得到灵敏度为4 102 rad/g，谐振频率为302.4 Hz。

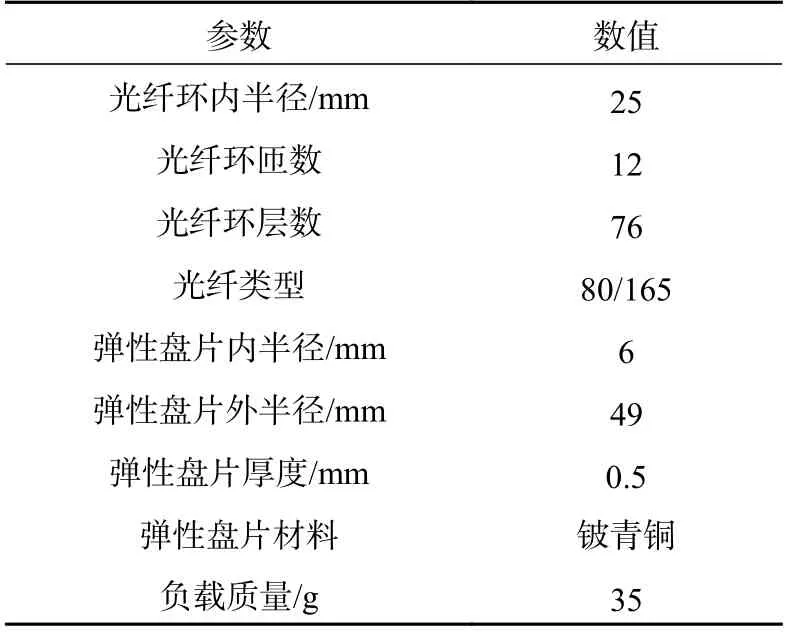
表1 盘式光纤加速度计制作参数

2 有限元仿真

采用有限元仿真软件建立基于多匝光纤环的盘式光纤加速度计拾振结构的仿真模型。

采用的有限元仿真软件可以对加速度计的拾振结构进行比较精准的几何建模和材料参数设置，并对模型施加非常接近实际情况的固体力学条件。采用表1的参数建立仿真模型，进而可以通过软件计算得到光纤环的应变分布和拾振结构的谐振频率，由光纤环的应变分布可以很方便地计算出加速度计的灵敏度。

采用二维轴对称方法建立拾振结构的几何模型，如图2所示。即在经过对称轴的截面上建立二维几何模型，仿真软件会将该二维几何模型绕对称轴旋转360°，形成三维几何模型。

图2 拾振结构的截面和局部放大

对模型施加沿对称轴方向的g=9.8 m/s2的重力场，采用稳态研究得到截面上的环向应变分布，如图3所示。

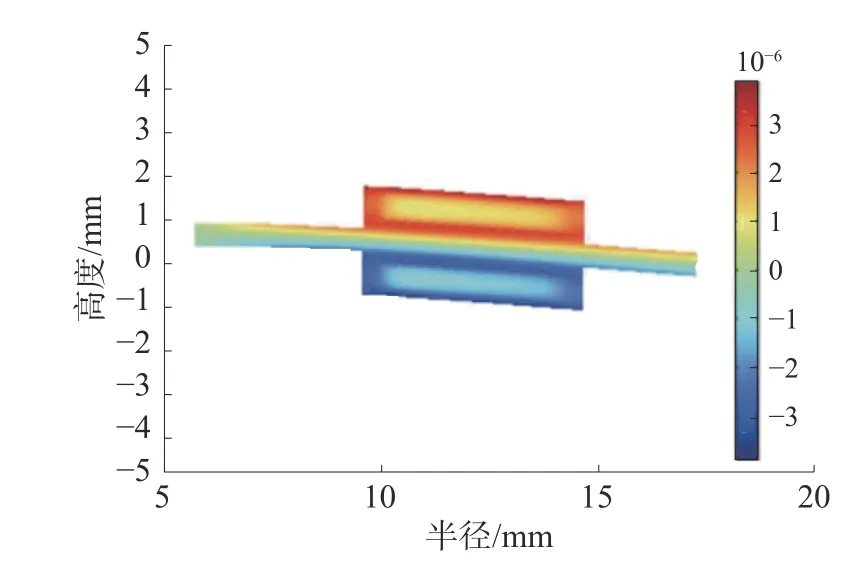
图3 环向应变分布

通过二维截点可以获得每一圈光纤纤芯的环向应变和周长改变量，求和得到一个光纤环的长度改变ΔL，代入式(5)即可得到仿真灵敏度，其值为2 563.25 rad/g。

采用特征频率研究即可得到拾振结构的仿真各阶谐振频率，其中一阶谐振频率最小，为250.38 Hz。

可以看出，由理论模型和仿真模型得到的灵敏度是相差较多的，下面对产生这种误差的原因进行分析。

图4是没有粘接光纤环的弹性盘片表面的环向应变分布，可以看出理论计算结果和仿真结果吻合较好。

图4 弹性盘表面环向应变分布

在理论模型中将粘接光纤环的弹性盘等效为一个均匀介质的圆盘，然而实际上光纤环只覆盖了一部分弹性盘。图5是光纤环粘接在弹性盘内侧时环向应变的理论计算结果和仿真结果，从仿真结果可以看出，弹性盘内侧的环向应变相比趋势线明显较小，这是因为在粘接光纤环的位置，弹性盘具有较大的刚度，而理论模型不能体现这一特点。因而对于光纤环的环向应变，仿真结果小于理论计算结果，产生仿真和理论计算之间的误差。

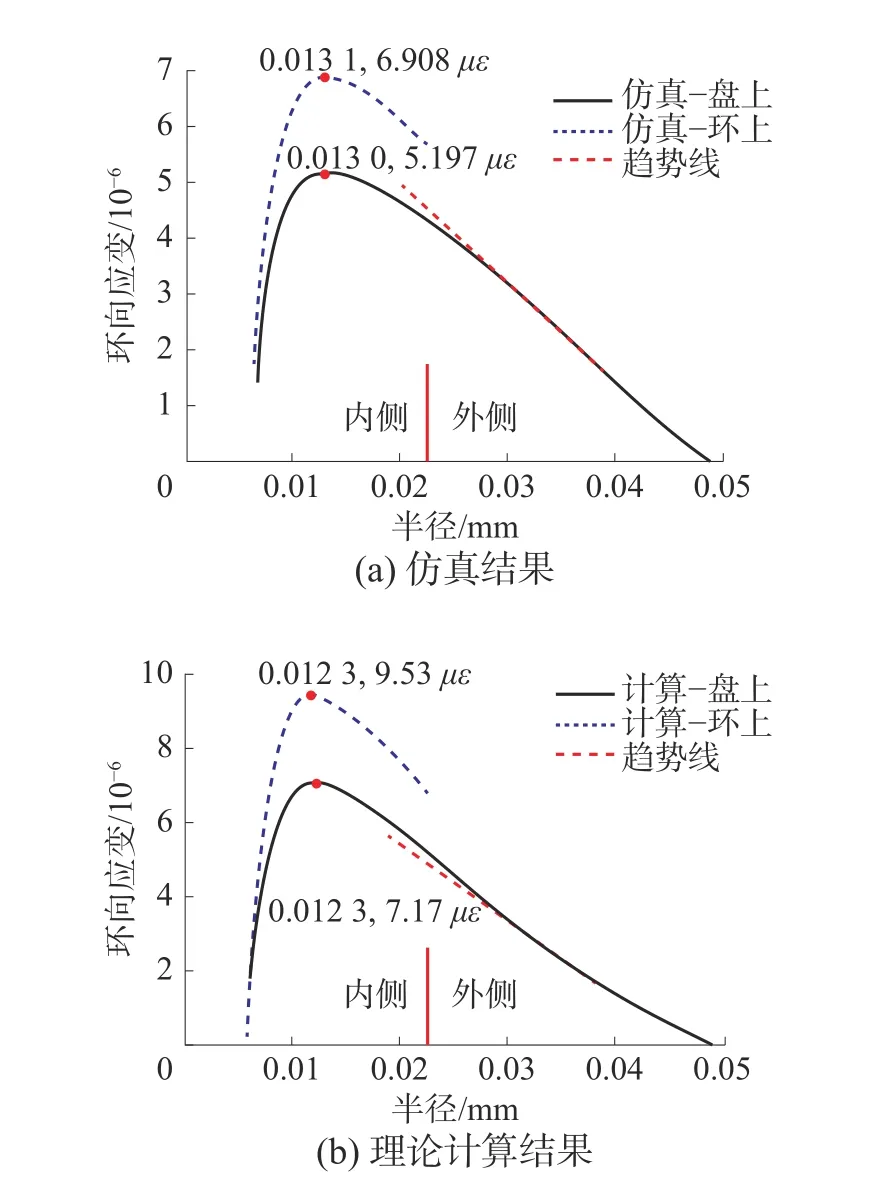
图5 环向应变分布对比

光纤环和弹性盘属于不同材质，二者还需用胶来粘接，应变无法完全从一种材料传递到另一种材料，存在应变传递率。应变传递率与材料的力学参数和几何参数都有关，无法将应变传递率进行定量计算，这会导致理论计算结果和仿真结果之间的偏差。

3 实验测试

按照表1的参数实际制作了盘式光纤加速度计，并对其进行测试，测试系统如图6所示。参考加速度计为石英加速度计，振动台产生的振动信号同时施加到盘式光纤加速度计和参考加速度计上，计算机可以同时得到2个加速度计的输出信号，参考加速度计从而可以对盘式光纤加速度计进行标定。

图6 光纤加速度计测试系统

进行谐振频率测试时保持参考加速度计测得的加速度幅值恒定，调节振动台的振动频率，得到盘式光纤加速度计的幅频特性曲线，如图7所示。实际制作的盘式光纤加速度计的谐振频率在212 Hz 附近，仿真得到的谐振频率与实验结果相差18.1%；在150 Hz 以内盘式光纤加速度计的响应稳定，因此该盘式光纤加速度计的工作带宽为150 Hz。

图7 盘式光纤加速度计幅频特性曲线

测试灵敏度时使振动台产生40 Hz 的振动信号，改变振动信号的幅度并对盘式光纤加速度计的输出信号进行测量，得到盘式光纤加速度计的加速度响应曲线，如图8所示。可以看出研制的盘式光纤加速度计对外界加速度的响应是非常线性的。曲线的斜率为盘式光纤加速度计的灵敏度，为2 834.29 rad/g，仿真得到的灵敏度与其相差-9.6%。

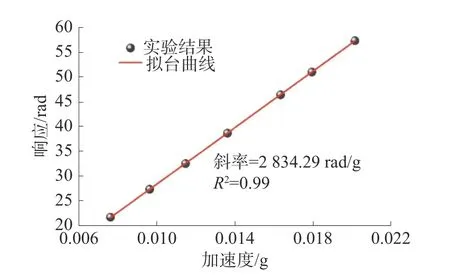
图8 盘式光纤加速度计加速度响应曲线

4 结论

本文建立了基于多匝光纤环的盘式光纤加速度计的理论模型与有限元仿真模型，并对研制的盘式光纤加速度计进行了实验测试，得到如下结论：

1)理论模型给出了灵敏度和谐振频率的表达式，但在准确度上还有提升空间；

2)实验测得的灵敏度为2 834.29 rad/g，谐振频率为212 Hz，仿真模型得到的灵敏度和谐振频率分别和实验结果相差-9.6%和18.1%；

3)本文建立的理论模型和仿真模型对基于多匝光纤环的盘式光纤加速度计的研制具有重要的指导作用。