基于点核积分的放射源定位方法
龙泽宇,刘永阔,杨立群,陈志涛
哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001
随着核技术应用的日益广泛,各类放射性源的安全问题显得尤为重要。由于放射源放出的射线人眼无法观测到,因此工作人员无法直接确定放射源的位置,放射源一旦“失控”,可能会严重威胁人们的身体健康甚至生命安全。如何快速准确地对放射源进行定位是核安全领域的重要研究课题。从查阅的国内外相关文献来看,针对放射源定位的研究通常分为2类:一是放射源搜寻定位,其中应用比较多的是基于方向探测器的搜寻定位方法,国内外研究人员根据放射源的辐射特性设计出各种各样的探测器,由人工手持或是车载,根据探测器给出的放射源方向信息,在移动过程中不断靠近放射源的位置[1-2],应用较少的则是γ 相机这类对辐射区域直接进行“热点”成像从而进行寻源的方法[3];二是放射源估计定位,与搜寻定位不同,此类方法并不依靠仪器对放射源进行寻找,而是利用辐射环境中部分探测点的剂量信息对放射源的位置直接进行大致估计[4-5]。然而,目前的这2类方法又都有着各自所面临的困境。第一类方法虽然定位精度高且定位结果可靠,但依靠人工直接在辐射环境下进行搜寻工作有悖于辐射防护中合理可行尽量低的原则(as low as reasonable practical,ALARP),若辐射场强度较高且搜寻时间过长,则可能会给工作人员的身体带来不可逆的损伤,而车载类探测器和γ相机则受制于高昂的成本;第二类方法的主要问题则是所需要的探测点数量通常非常多,或是无法应用于有障碍物遮挡的情形下,这使得此类方法的适用性较差。
针对目前放射源估计定位中存在的问题,本文提出了一种基于点核积分的放射源定位方法,该方法可以直接利用辐射环境中探测点处的剂量率值对放射源进行定位分析,需要的探测点数目较少,且由于点核积分方法的引入,解决了环境中障碍物遮挡的问题,极大地提高了方法的适用性。同时,本文利用蒙特卡罗程序MCNP5设计了虚拟仿真实验,验证了该方法的有效性。
1 点核积分
目前在辐射防护领域中,用于辐射剂量计算的方法主要包括蒙特卡罗方法和点核积分方法2种[6]。蒙特卡罗方法又称随机抽样方法,通过对大量粒子进行输运计算来模拟真实的物理过程,使得计算结果通常都能很好地符合实际情况,因此被广泛应用于对辐射剂量精确度要求较高的情况下。点核积分方法则是一种半经验性的计算方法,通过引入累积因子来考虑散射光子对辐射剂量的贡献,与蒙特卡罗方法相比,虽然计算精确度有所下降,但计算效率得到了极大提升,这也是能够对放射源进行快速定位的关键原因。
1.1 计算公式
点核积分的核心思想是将放射源按照几何形状离散为若干各向同性点源的集合,单个点源在探测点处的剂量率为[7]
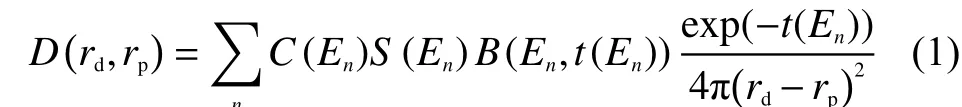
式中:En为放射源的光子能量,MeV;rp与rd则分别为点源与探测点的位置;C(En)为光子通量到剂量率之间的转换系数,(mSv·h-1)/(1·cm-2·s);B为累积因子;S(En)为En能光子对应的源强;t(En)为平均自由程数,计算公式为
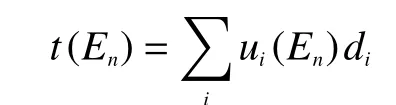
式中:i为点源和探测点之间的屏蔽层序号;ui(En)为En能光子在第i层屏蔽中的线减弱系数,1/m;di则为光子在第i层屏蔽中的穿行距离,m。将式(1)按放射源空间体积进行积分,即可得到整个放射源在探测点处的剂量率:

1.2 累积因子
探测器探测到的γ光子包括放射源发射并直接到达探测点处的直穿光子,也包括出射光子与路径上的屏蔽物发生相互作用后产生的散射光子。因此,探测点处的剂量由计算简单的直穿光子项和计算困难的散射光子项这2部分组成[8]。点核积分通过引入累积因子B来对散射光子项进行考虑,其物理意义为在考察点r处,某一辐射量的总值与直穿光子造成的同一辐射量的比值:

式中:x为光子平均自由程数;a、b、c、d、xk为不同光子能量、不同材料下的参数。
2 放射源定位
2.1 问题描述
在实际情况中,放射源都有着一定的空间体积,在进行计算的时候应考虑离散。但当探测点和放射源之间的距离是源最大线度的10倍以上时,就完全可以将放射源视为点源处理。即使只有5~7倍,剂量计算的误差也不会高于5%[10]。在放射源定位的问题上,放射源体积与整个辐射区域相比通常可以忽略,因此在本研究中,将所有的放射源均视为点源来处理。整个问题可由图1所示的平面示意图进行简单描述。
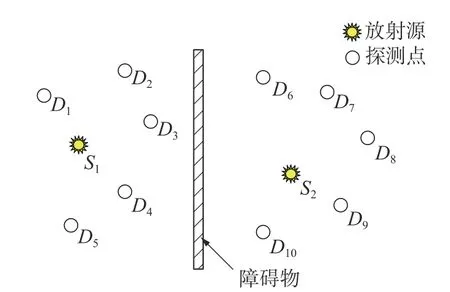
图1 放射源定位问题示意
其中探测点可由参数向量D n=[xn yn dn](n=1,2,…)进行表示,其中(xn,yn)为第n号探测点的平面坐标,dn为该探测点处的剂量率实测值;放射源可由S m=[xmymEm](m=1,2,…)进行表示,其中(xm,ym)为第m号放射源的平面坐标,Em为该放射源的γ光子能量。
2.2 区域离散
从理论上来说,在进行放射源定位之前,整个辐射区域内任意点都有可能是该定位问题的解,因此为了减小解集的规模,同时也为了便于对放射源的定位结果进行描述,本文将辐射区域进行栅格化处理[11]。使用边长为l的正方形栅格来划分辐射区域,如图2所示,以最终解得的栅格的中心坐标来表示放射源的定位结果。
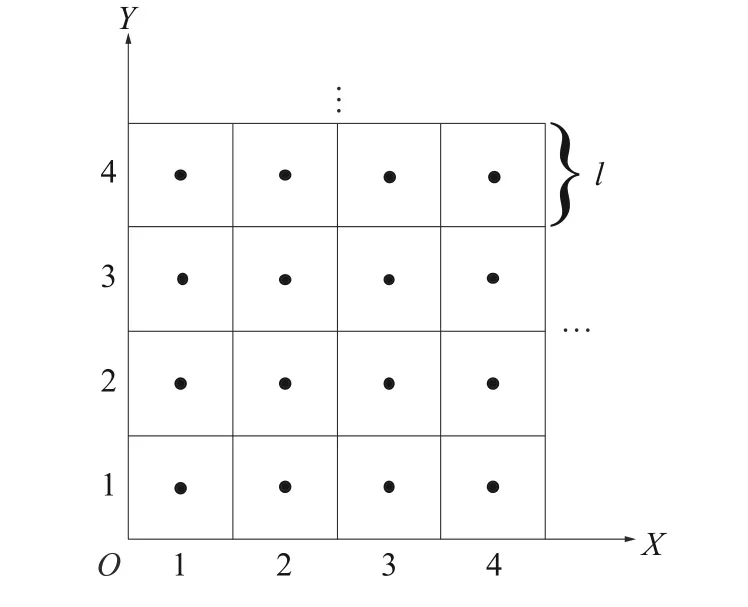
图2 辐射区域栅格化示意
对于离散化的辐射区域,如果某栅格被障碍物占据,则可以直接认为该栅格为非解,在计算过程中可以直接跳过。另外,栅格的边长l也会对定位结果产生很大的影响,如果栅格过大,栅格的密度就会很小,最后的定位精确度就会变差;如果栅格过小,栅格的密度就会很大,会使计算效率明显降低。通常情况下,栅格的边长l取1 m 即可。
2.3 放射源源强反解
假设辐射环境中总共存在有N个探测点以及M个放射源,按照点核积分理论,每个探测点处的剂量率应为各放射源贡献之和,即


1)列主元消去算法。该算法是为减小方程组求解过程中的舍入误差而提出的一种算法,与普通消去方法不同,其在每一次消元前都要进行一次行替换,以避免绝对值很小的元素直接作为除数的情况出现。计算过程可大致分为选主元、行替换、消元、回代求解4个步骤。
2)NNLS算法。针对方程组Ax=b,其非负线性最小二乘问题在数学上一般表示为
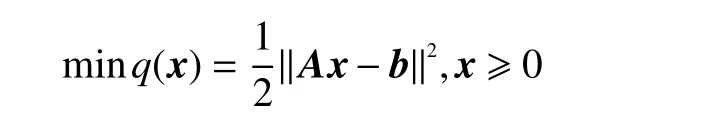

2.4 可信度计算

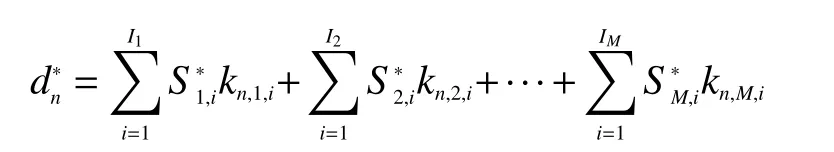
需要指出的是,由于点核积分计算结果与实际剂量率总会存在一定的差异,因此此处的可信度并非绝对可信度,而是相对可信度。当遍历完所有的栅格后,即可选取其中可信度最高的栅格作为最终的放射源定位结果。
2.5 并行加速
尽管已经将辐射区域进行了离散,但当辐射区域面积较大时,划分的栅格数目仍然会很多,从而需要进行大量的复杂方程组求解。因此为了提高计算效率,本文引入OpenMP[14]并行机制来加快计算速度。OpenMP 是一种适用于多核CPU的并行编程接口,对于需要进行循环的结构块,OpenMP可以通过派生分支线程的方式来使其同时进行计算,且当所有的分支线程执行完成后,才会执行下一语句,不同线程里的结构块并不会发生冲突,其加速效率取决与CPU 核心的数目。引入OpenMP并行机制后的完整放射源定位方法流程如图3所示。

图3 放射源定位方法流程
3 实验验证及其分析
3.1 单放射源定位实验
为验证本文所提方法的可行性及有效性,通过蒙特卡罗程序MCNP5设计了如下虚拟仿真实验:在20 m×20 m 的辐射环境中,建立笛卡尔坐标系,环境中心处为(0 m,0 m),其中有一放射源S1,实际位置为(4.5 m,4.5 m),其核素为Co-60,产生2 种能量的γ射线,分别为1.173、1.332 MeV,场景中的障碍物为普通混凝土墙,厚度均为15 cm,密度取2.56 g/cm3,并随机选取8个探测点,如图4所示。
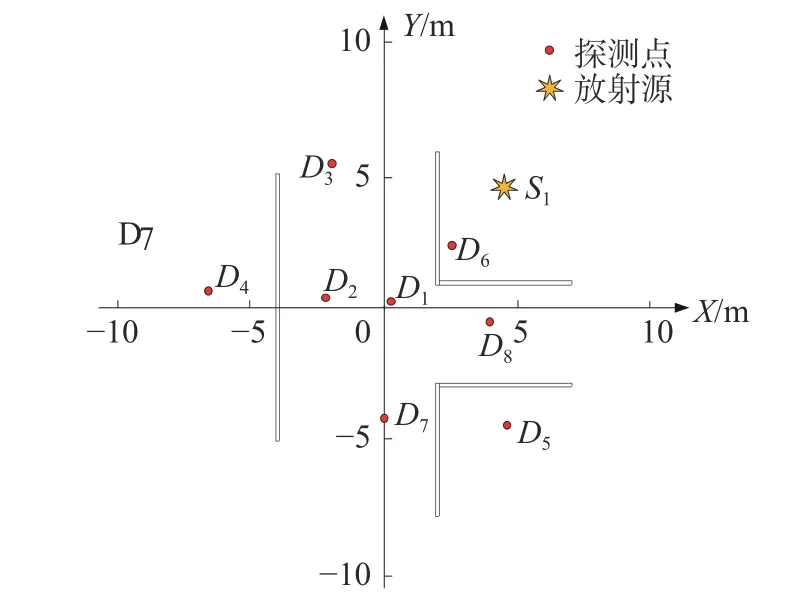
图4 单放射源定位实验
在随机设定好放射源的源强后,即可直接通过MCNP5程序对各探测点剂量值进行计算,因为实际探测器会有一定的不确定度,因此将计算结果上下浮动10%,从而更好地接近真实情况,最终结果见表1。
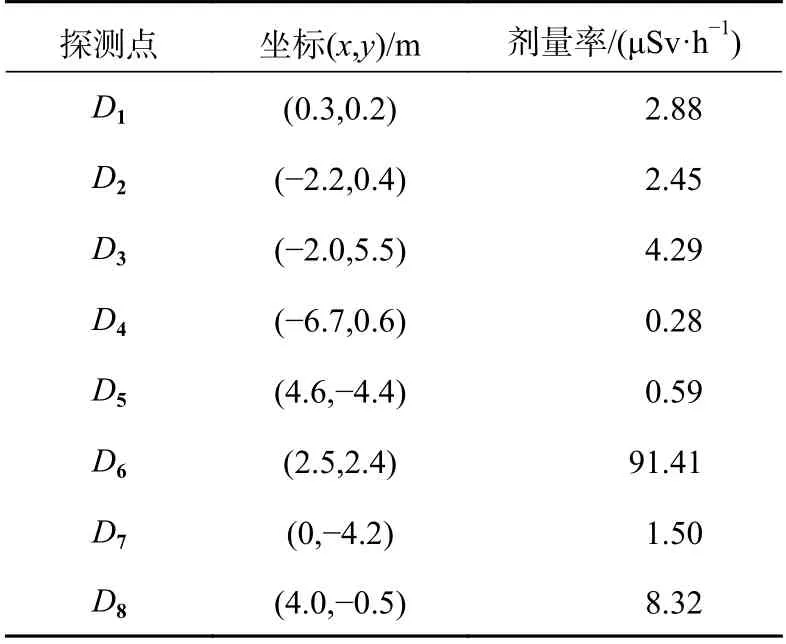
表1 探测点及剂量率
利用C++编程语言实现本文算法,并根据上述设计好的案例进行实验。栅格划分的边长设为1 m,计算结果经处理后如图5所示,计算部分耗时约为0.15 s。仿真实验是在Windows10、64 位操作系统环境中进行的,处理器为Intel Core i5-9300H 2.40 GHz。
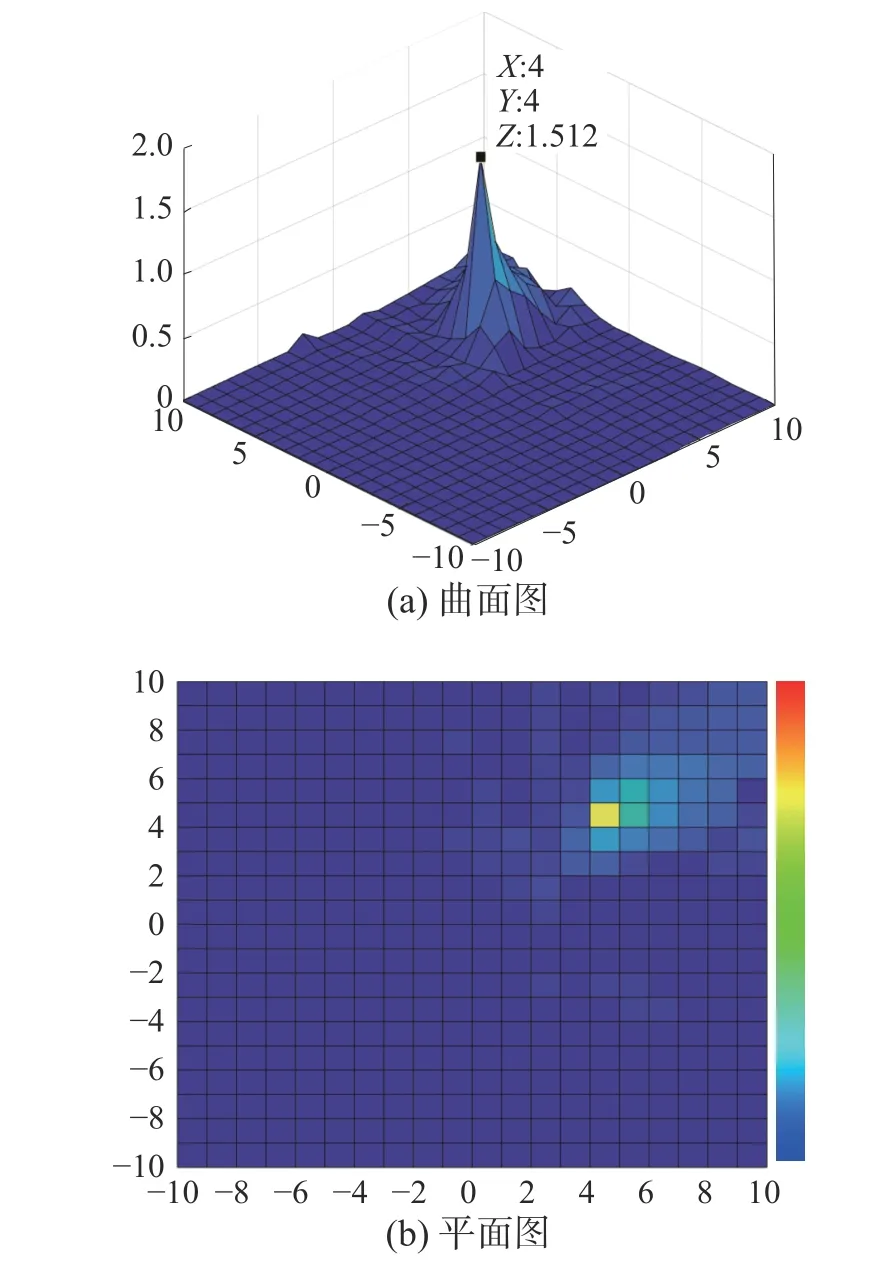
图5 单放射源定位实验结果
从图5中可以看出,当栅格边长为1 m 时,最终确定的放射源位置为(4 m,4 m),非常逼近放射源的实际位置,且可信度较高的其他栅格也均处于实际位置的周围,证明了本文所提方法对单放射源定位有着较高的可行性。
3.2 双放射源定位实验
与单放射源定位实验相比,其他条件不变,放射源S1的位置仍为(4.5 m,4.5 m),另外在区域左下角(-2.6 m,-3.8 m)处增加一个放射源S2,核素种类为Cs-137,其γ光子能量为0.661 MeV,如图6所示。
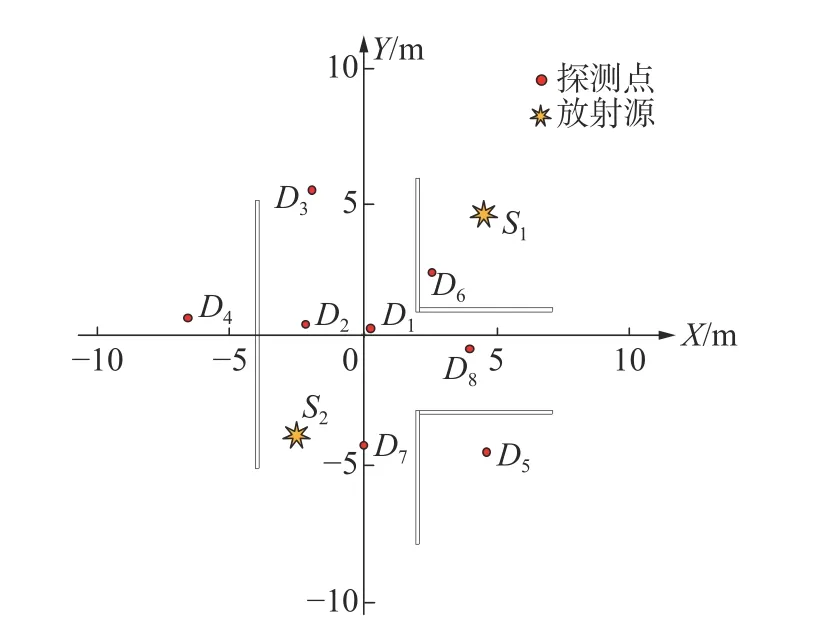
图6 双放射源定位实验
通过MCNP5程序对各探测点进行计算并随机上下浮动10%后的剂量率见表2。
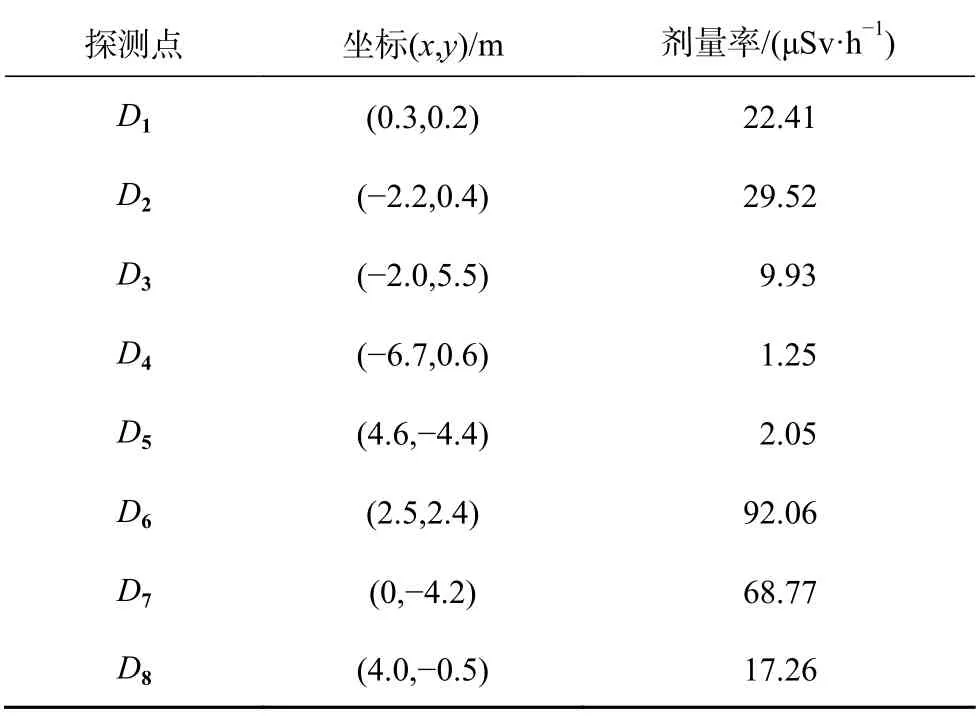
表2 探测点及剂量率
栅格划分的边长仍然为1 m,计算部分耗时约为25 s,其中可信度最大的前8种位置如表3所示,表中总偏差为各放射源定位结果和实际位置的偏差之和。
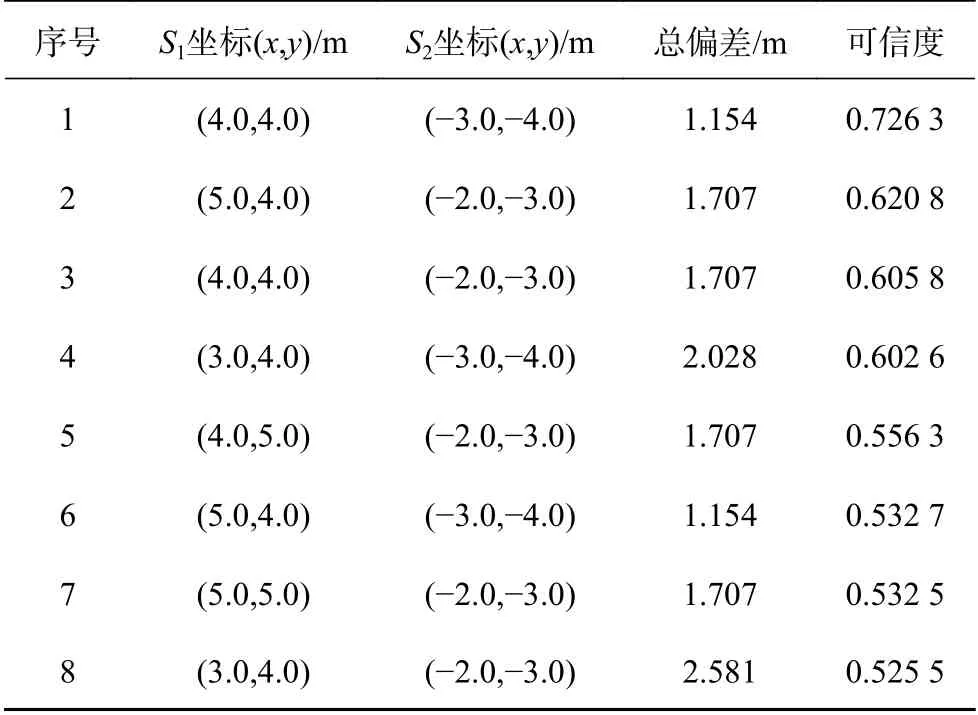
表3 双放射源定位实验结果
从表3中可以看出,最终确定的放射源S1、S2的位置分别为(4.0 m,4.0 m)和(-3.0 m,-4.0 m),与放射源的实际位置都比较贴近,且可信度较高的其他几种位置也均处于实际位置的周围,证明了本文方法对多放射源定位同样可行、有效。
4 结论
本文将点核积分引入放射源的定位之中,提出了一种新的放射源定位方法,并通过MCNP5程序进行了虚拟仿真实验,通过实验结果分析可以得出以下结论:
1)该定位方法需要的探测点数量较少,且能在有障碍物遮挡情况下对放射源进行定位,比已有的放射源估计定位方法有着更高的适用性;
2)该定位方法对单放射源和多放射源都有着较高的可行性,但随着放射源数量的增加,所需要的计算时间也会快速增长,因此在后续的工作中需要对该算法继续进行优化,以进一步降低计算所需要的时间。

