基于瞬时相位新特征的数字调制信号识别
孙华泽,张晓林
哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001
调制识别一直都是非合作通信的重要一环,实际中大部分都采用统计识别的模式来完成调制识别[1]。这种方法需要先对信号的特征进行提取,再通过分类器分类[2]。因此目前对调制方式识别的研究方向大致分2类:一类是将研究的重点放在新特征的提取上,包括高阶累积量[3]、循环谱[4]、小波特征[5]、星座图特征[6]等;另一类是采用机器学习作为分类器,比如随机森林[7]、支持向量机[8]、卷积神经网络[9]、AdaBoost[10]等,这些分类器通过大量的数据训练与测试,与传统决策树分类器相比,在使用相同特征参数的条件下可以获得更高的正确识别率。近年来,随着特征的种类和提取方法越来越完善,一些基于经典特征提取算法的新特征被相继提出并应用于调制识别中。文献[11-12]中作者用循环谱特征图像分析方法,通过汉明距离测度枚举训练和测试数据所得到的特征参数之间的差异,成功实现了多种调制信号的分类工作。文献[13]将信号的各种熵特征与特征选择算法相结合,运用5种不同的集成学习分类器完成了对多种数字调制信号的分类工作。文献[14]提出一种压缩时间高阶循环累积量。文献[15]为了解决循环累积量特征在高采样率下使用受限问题,将压缩感知框架引入调制识别体系中,并且将文献[14]中的新特征作为对照目标进行研究。然而,传统的瞬时特征和决策树分类器由于原理简单、容易硬件实现,目前仍然被广泛使用并被继续深入研究。本文针对2ASK、4ASK、8ASK、2PSK、4PSK、8PSK这6种数字调制方式,在文献[16]提出的瞬时特征基础上,利用MPSK 调制的非线性相位取值的差异性提取特征,完成了4PSK 与8PSK 的类内识别;同时从瞬时频率的角度提取特征完成了4ASK 和8ASK 的调制识别。
1 调制识别流程
基于统计模式理论的调制识别方法主要包含3个核心技术单元,即信号预处理、特征参数提取和分类器判决。本文的重点在于特征参数提取,因此文中将着重介绍新提出的区分4PSK 和8PSK 的瞬时特征——分段相位均值最大值,并从理论和仿真的角度完成对此特征的分析。
1.1 调制信号瞬时特征

鉴于由式(1)得到的信号相位限制在[-π,π],所以需要对相位进行展开,并减去载频分量,才能得到信号的非线性相位[17]。
1.2 经典瞬时特征提取
对于待识别的6种调制方式,一般通过提取信号的瞬时幅度、瞬时频率、瞬时相位等5个瞬时特征来完成调制识别。对于本文所使用的传统特征参数,因为在其他论文中也多次提及,所以这里只列出所使用的特征,并不进行详细介绍。
1)归一化中心化瞬时幅度功率谱密度最大值:

2)非弱信号段中心化瞬时相位非线性分量绝对值的标准偏差 σap:

3)非弱信号段中心化瞬时相位非线性分量的标准偏差 σdp:

该特征表征信号瞬时相位的变化情况。
4)中心化瞬时频率的均方值:

该特征可以完成4ASK、8ASK 这2种ASK 信号的类内识别。对于ASK 信号而言,只有符号0 对应的调制信号是没有载频的,其余符号对应的调制信号都存在载频,只是幅度信息不一样。这样在求瞬时频率时,符号0对应的瞬时频率为0,其余的符号所对应的就是正弦波2个相邻采样点之间的相位差值。而从统计角度分析,2ASK取每个符号的概率为0.5,4ASK 为0.25,8ASK 为0.125。当每个符号等概率出现时,2ASK、4ASK、8ASK 这3种调制方式里符号0出现的概率依次是0.5、0.25、0.125。对于瞬时频率来说,符号0 出现的概率越大,相应的瞬时频率的离散程度就越大。所以2ASK 的该特征值最大,4ASK 其次,8ASK相对来说最小。此特征在不同信噪比下的仿真结果如图1所示,从图中可以看出,在信噪比大于10 dB时,4ASK 与8ASK 的特征值差异明显,可以用此特征区分。
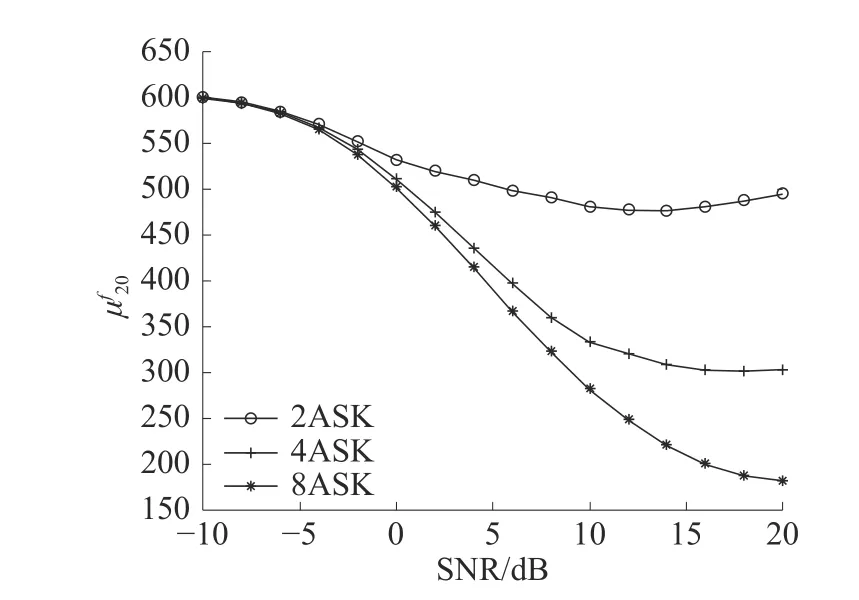
图1 随信噪比变化曲线
2 分段相位均值最大值
对于4PSK 和8PSK 这2种利用多个不同相位来传递基带序列的调制方式,目前已有的调制识别方法是利用高阶累积量[3],或者使用瞬时相位平方的标准差去区分。一般高阶累积量需要数量较多的码元,才能将相位调制所具有的特征展现出来。文献[18]提出用特征瞬时相位非线性分量平方值的标准偏差Vph来区分4PSK 和8PSK,此特征的仿真曲线如图2、3所示。

图2 V ph随仿真次数变化曲线

图3 V ph随 信噪比变化曲线
由图2可知,此特征并不稳定,在实际应用中很难找到比较合适的门限来区分这2种调制方式。而从图3可以看出,在对此特征值多次取平均后,可以在信噪比高于5 dB时完成4PSK 与8PSK的区分。针对该特征波动范围大,不适合用决策树分类这些缺点,本文提出了一种新的特征提取方法,即在已知符号速率的前提下,针对瞬时相位特征进行提取,并以此完成PSK 的类内识别。
对于2PSK、4PSK、8PSK 这3种相位调制,在一个符号内,3种相位调制的相位分量保持不变,在符号变化的位置,其相位值也发生了突变。在不考虑相位突变位置所产生的尖峰毛刺前提下,2PSK 瞬时相位的最大值为π;4PSK 瞬时相位的最大值为7π/4;8PSK 瞬时相位的最大值为 15π/8。为了将最大值特征的差别显现出来,对瞬时相位的所有值都除以常数π/4,这样2PSK 相位的最大值为4,4PSK 相位的最大值为7,8PSK 相位的最大值为7.5。
但是,在有噪声的情况下,每一个符号内的相位信息受噪声的干扰较大,图4所示是4PSK 调制在信噪比为5 dB时的非线性相位。从图中可以看出,噪声的存在破坏了信号原本的特征,无法准确地确定相位的最大值。

图4 信噪比为5 dB下4PSK 相位

在无噪声的条件下,仿真得到的3 种MPSK调制的该特征取值如图5所示。图中2PSK、4PSK、8PSK 的特征值分别为5、6、7,与上述的理论值存在差异。
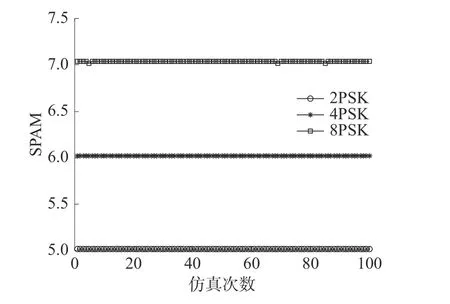
图5 SPAM 随仿真次数变化曲线
仿真得到2PSK 相位如图6所示。从图中可以看出2PSK 的2个相位取值是π/4和 5π/4,并不是0和π,这是因为仿真程序中,基带序列是取值为±1的双极性序列,直接用双极性序列去乘以载频,这样虽然相位突变值是π,但是突变位置前一点的相位并不是0,而是π/4,所以会与理论值存在误差。

图6 2PSK 相位
当采样速率是载频的8 倍时,4PSK 和8PSK仿真得到的瞬时相位如图7、8所示。从图中可以看出,在8 倍采样率的条件下,4PSK 的部分相位取值为1.568 5、3.142 8、4.697 4、6.28,与理论值相差π/4;8PSK 的部分相位取值为1.57、2.37、3.1、3.9、4.7、5.5、6.2,与理论值相差 π/8。但是调制方式产生的程序和瞬时相位提取的程序,均符合已有文献对相关原理的阐述,因此初步怀疑可能是采样速率的影响。接下来就对采样速率进行分析。
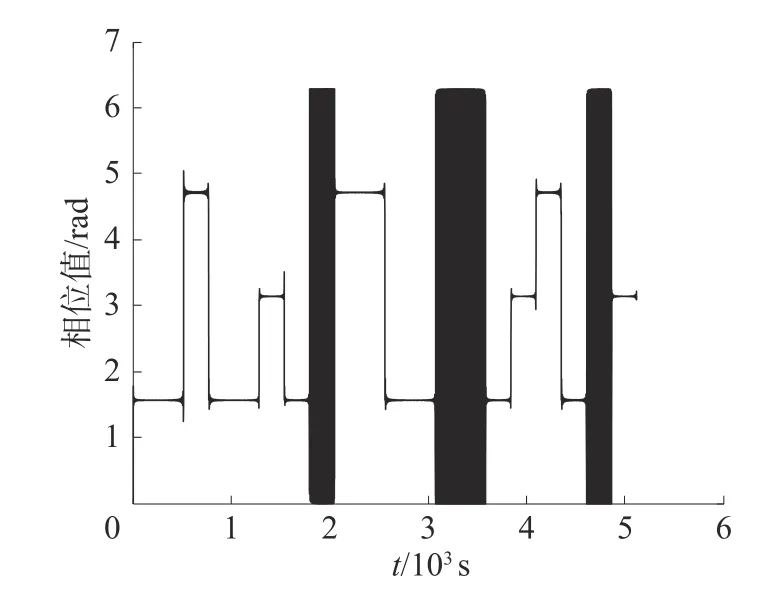
图7 4PSK 相位

图8 8PSK 相位
当采样速率分别为载频的16、32、64、128倍时,4PSK 和8PSK 相位取值如图9、10所示,部分相位取值已在图中标出。由图可知,对于4PSK和8PSK 调制,采样速率越高,相位的取值越接近理论值。但因为在实际应用中并不会用过高的采样率进行采样,所以本文后续仿真都采用8 倍采样进行,并考虑采样速率导致的相位偏差对特征值提取的影响。

图9 4PSK 相位
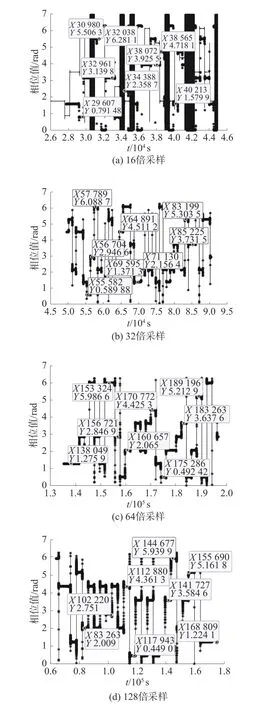
图10 8PSK 相位



图11 SPAM 随信噪比变化曲线
3 分类器设计
分类器采用传统的决策树分类器,此分类器因其结构简单、易理解、易扩展等优点而被广泛使用。针对本文的种调制信号,分类流程如下。
1)如果Rmax大 于阈值T1,则待识别信号属于MASK,否则属于MPSK。

3)对于MPSK 信号:如果 σap小于阈值T4则待识别信号为2PSK;如果 σap大于阈值T4,且SPAM大于阈值T5,则为8PSK;否则就是4PSK。
根据上述的特征和识别流程,在Matlab仿真下得到的6种调制方式的识别率如图12所示。仿真条件为基带符号速率Rs=500 Baud,载频fc=2 kHz,采样频率fs=8fc,符号个数为150个,信噪比范围为-10~20 dB,间隔为1 dB。由图10(c)可知,8ASK 受限于特征的选取,只有在信噪比高于10 dB时才能达到90%以上的正确识别概率,而其余的调制方式在信噪比高于4 dB时,正确识别率就可以达到90%以上。而图中显示的4PSK 在信噪比为-10 dB可达到80%以上的识别率,并不是因为特征的有效,而是因为按照本文所采用的决策树分类器,如果有一种调制方式最后无法分类,都会归到4PSK 调制,所以此时4PSK 的正确识别率其实已经不具有可信度,这也是决策树分类器的一种固有缺陷。

图12 决策树分类识别率
为了更好地评价本文所提出的新特征在对4PSK 和8PSK 这2种信号的分类性能,与文献[17]中所构造的具有相同功能的高阶累积量特征A1进行对照仿真实验。在不同信噪比下,此2种特征对以上MPSK 信号的调制方式正确识别率如表1所示。

表1 2种特征提取算法识别率对照
根据表1中结果数据可知,当信噪比在-2 dB以下时,2种特征均已失效,出现了严重的误识别现象。但是当信噪比为2 dB时,本文提出的SPAM特征明显好于经典的高阶累积量特征A1,且随着信噪比增加,SPAM特征对于2种信号的识别率均大于97%,而高阶累积量特征A1由于受到码元数量的限制,在较高信噪比条件下的分类性能稍逊于SPAM特征。
4 结论
本文针对待识别的6种调制方式,重点研究了用来区分4PSK 和8PSK 所提取出的新特征SPAM的计算流程,同时分析了特征SPAM的取值与理论值之间的差异以及产生原因。与现有特征Vph和高阶累积量A1相比SPAM的取值更为稳定,且取值差异更明显,适合用传统决策树进行区分。仿真结果表明,对于本文提出的新特征,在信噪比高于4 dB时可以正确识别4PSK 和8PSK 数字调制方式,且正确识别概率可以达到90%以上。由于SPAM特征为信号的瞬时信息特征,因此在工程实践中更方便应用。
然而,码元速率的估计误差可能会影响此特征的分类性能,所以这将是下一步需要深入研究的问题。

