被上游建筑遮挡的下游建筑表面风压CFD模拟的可靠性研究

付琳莉，殷维,，王天文，郝小礼，刘何清，张国强，陈翚

(1.湖南科技大学 a.土木工程学院；b.资源与安全工程学院，湖南 湘潭 411201；2.湖南大学 建筑学院，长沙 410007)

研究城市通风或建筑风环境的主要目的是探索建筑之间和建筑内外的气流运动及污染物扩散规律，例如，自然通风是其中主要研究内容之一[1]。建筑间气流的现场测量存在不稳定性、多样性等特点，而风洞手段结合简化建筑模型，能够得到相对稳定可靠的实验结果[2-4]。另一方面，越来越多的研究人员运用更为方便和低成本的计算流体动力学(Computational Fluid Dynamics，简称CFD)来研究此类问题，其中,建筑内外的气流耦合模拟成为研究热点[5-7]。

Straw等[6]的通风研究表明，与测量的体积流速(偏差为28%～32%)相比，压力系数与孔口方程的结合使用，并不能较为准确地预测体积流速，当存在(大)开口时，其压力系数与同一主体上的压力分布不对应。对于自然通风的研究，Kavara等[3]针对一个单区两开口的一般性模型进行了风洞实验，研究分为两对称墙上开洞与侧墙上开洞两种情况。结果表明，经典的伯努利方程计算出的气流流量公式与实际情形相差较大，建筑之间的遮挡会极大地削弱自然通风的效果，两个建筑的互相遮挡是其最简单的形式。在现有遮挡研究中，主要讨论两建筑之间水平方向、垂直方向对建筑荷载的影响[8-10]。基于Kavara等[3]的研究，Tominaga等[11-12]在相同模型下进一步探讨了污染物扩散情况，此外，还讨论了建筑周边无遮挡和有遮挡两种情况，发现当周边有遮挡建筑时，穿过建筑的气流量将下降30%，但Tominaga等仅研究了单区间建筑内部穿堂风的分布规律。Van Hooff等[13]基于Tominaga等[11]的实验结果，针对无遮挡的情况，运用CFD方法进行了模拟研究。结果显示，所有的雷诺平均模型(Reynolds Average Navier-Stokes，简称RANS)可以较好地模拟建筑内部的气流场，却无法较好地模拟湍流动能分布，而大涡模型(Large Eddy Simulation，简称LES)则可以较好地模拟出所有参数，包括速度、湍流动能和换气量。但Smal[14]针对Tominaga等[12]的有遮挡情况，运用稳态雷诺平均NS方程模型与非稳态雷诺平均NS方程(RANS与URANS)进行了模拟。结果显示，所有模型所得到的速度和湍流度模拟结果都与实验结果的吻合度较差，只有RSM湍流模拟出的室内气流的风向与实验相一致。

以上研究表明，CFD模拟对于有遮挡后方的气流预测准确性较差，且未讨论上游建筑有孔时对下游建筑的影响，即未见穿堂风对下游建筑表面压力的影响。针对上游建筑为有孔遮挡与无孔遮挡两种遮挡情形，将CFD模拟结果与风洞实验数据进行严格对比，探究在提高模拟可靠性的同时，降低计算硬件要求与时间成本。

1 风洞实验设置

1.1 研究方案与模型

为了避免由实验模型造成的实验误差，上游与下游建筑采用与Karava等[3]相似的建筑模型，与Tominaga等[11]实验中的模型尺寸完全相同，与真实建筑比例为1∶ 100，上下游两个建筑的外形尺寸都为W×D×H=0.2 m×0.2 m×0.16 m，两建筑间的距离固定为2倍建筑宽度(0.4 m)。只讨论一个来流风向——垂直于上游建筑迎风面。实验对象分为两组：1)有孔遮挡，上游建筑为中空，且迎风面与背风面各有一个相同面积与位置的对称开口，开口位置位于迎风面和背风面中心，高度h=80 mm，开口面积为3.3×10-3m2；2)无孔遮挡，上游建筑同为中空建筑，但建筑各表面无开口，为封闭模型。两组实验模型如图1所示。压力系数测量点布置于下游建筑表面，建筑模型测点分布如图2所示。

1.2 风洞设置

风洞为一座水平直流吸入式单试验段低速风洞，风洞试验段长21 m、高3 m、宽4 m，使用尖顶和表面粗糙度的组合来创建近似3类大气边界层的流动风剖面。来流风平均速度服从幂指数为0.25的函数公式，见式(1)。

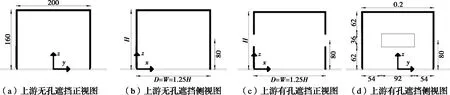
图1 建筑尺寸(单位：mm)

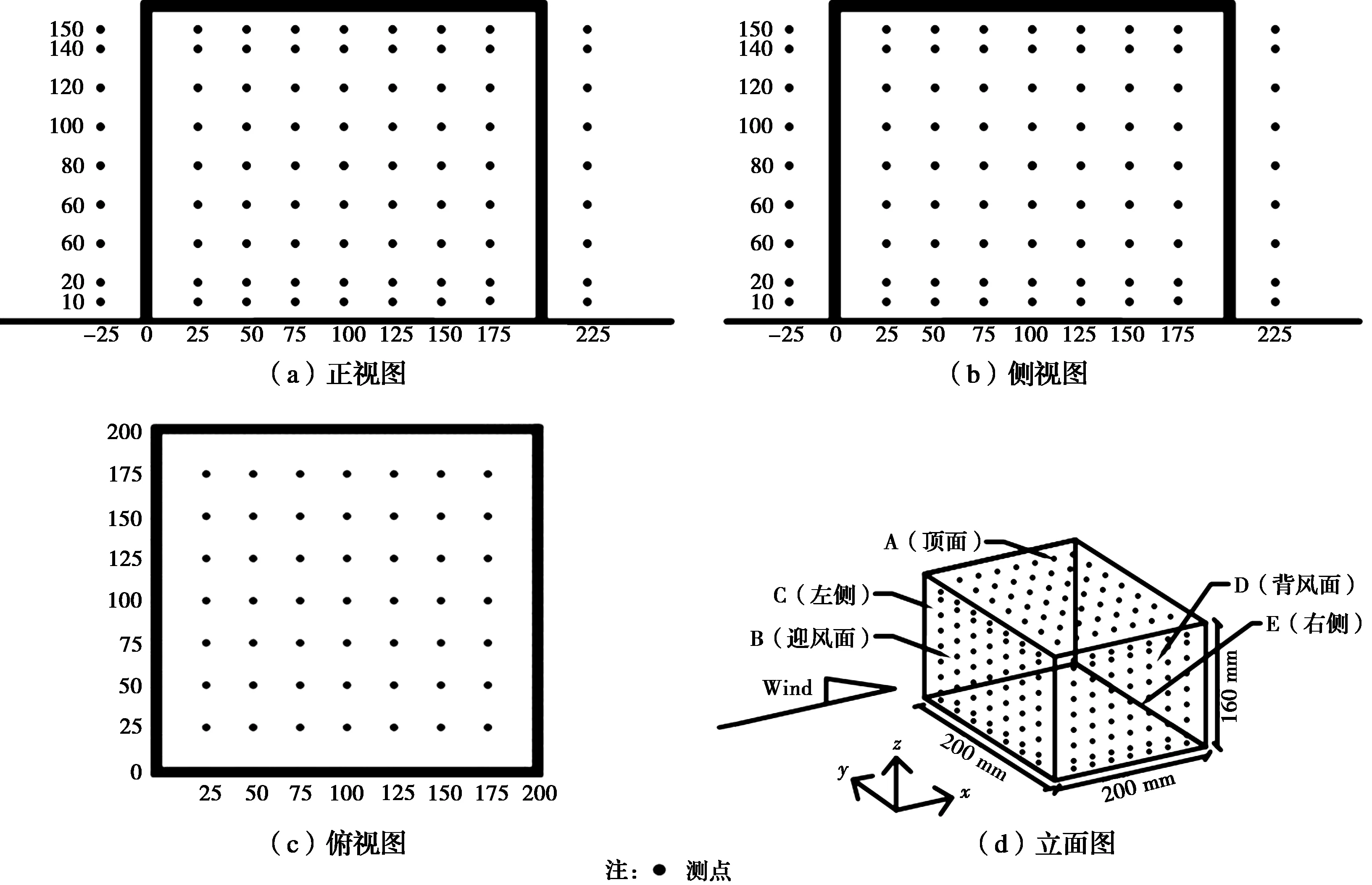
图2 下游建筑表面测点分布图

(1)

式中：UZ和UH分别为高度z和建筑高度H处的来流风平均速度。

通过测量来流风3个方向的分速度，拟合出湍流动能在高度上的近似曲线，见式(2)。

(2)

式中：κ(z)为高度z处的湍流动能。

图3为风洞中实测来流风速曲线与湍流动能曲线。风向垂直于建筑迎风面，在建筑物高度H处(0.16 m)测得风速(UH)为4.5 m/s，对应的雷诺数约为47 000。这个雷诺数与Tominaga等[11]实验中的45 000接近，达到雷诺数独立(Reynolds Independence，又称雷诺数无关)。3个月后的重复实验获得非常相似的结果，实验具有较好的重复性。

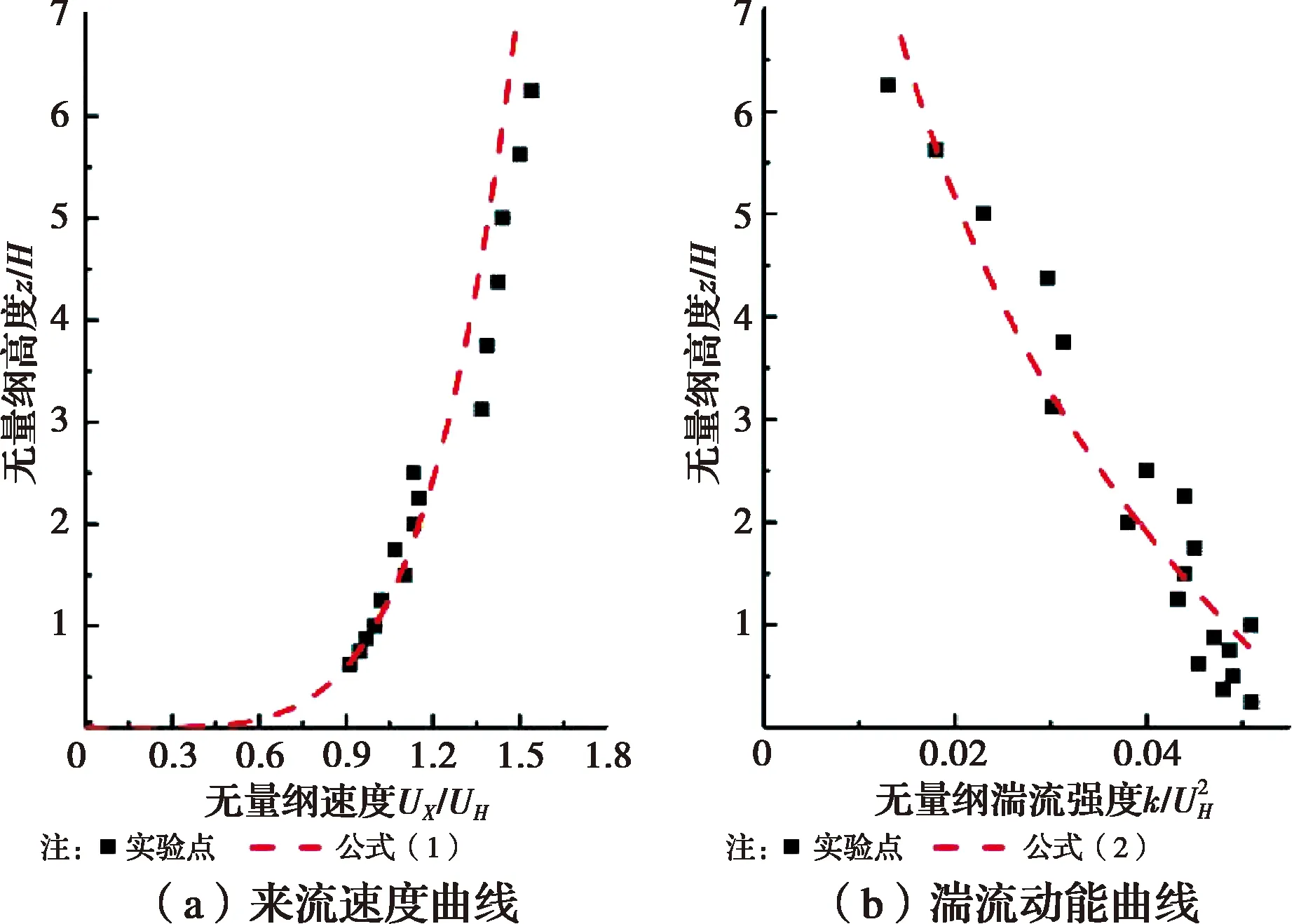
图3 风洞实验来流曲线图

采集的实验数据包括来流风速、风压、静压、湍流度等。实验采用三维脉动风速仪(TFI，Cobra Probe)进行风速测量；采用PSI公司的512通道电子压力扫描阀系统进行压力测量，测量时长为30 s，采样频率为332.5 Hz，采样点数为301个；可视化实验中的发烟试剂采用了15%的丙烯乙二醇溶液，发烟点位于上游建筑地面中心，为半径1 cm的圆形发烟口，发烟口高度距离地面2 cm，在风场稳定后持续发烟，发烟时长为60 s，采用摄像机记录可视化实验中各遮挡情形气流变化。

1.3 实验分组

在风洞中进行两组实验，分别为上游有孔遮挡与上游无孔遮挡，摆放模型图以及现场实验图如图4所示。

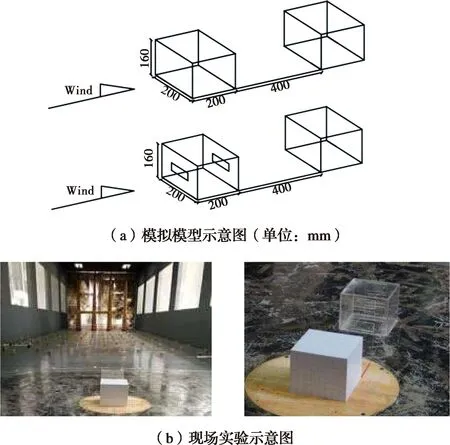
图4 实验图

2 CFD模拟设置与参数

2.1 计算域设置

计算模型与风洞实验中的模型相同，与真实建筑比例为1∶ 100，墙壁与天花板的厚度均为3 mm。计算域基于Tominaga等[12]和Blocken[15]的最佳实践指南构建，即从建筑物到计算域的顶部和两侧的距离为5H，下游建筑物背风面和计算域的出口边界之间的距离为15H。该区域的上游长度为建筑物高度的3倍(3H)，此距离可以限制进近流动剖面中意外的流向梯度的发生[15-16]。得到的计算域尺寸为5.32 m×1.8 m×0.96 m(L×W×H)，与Van Hooff等[13]研究中的计算域一致，计算域尺寸与建筑模型网格如图5所示。

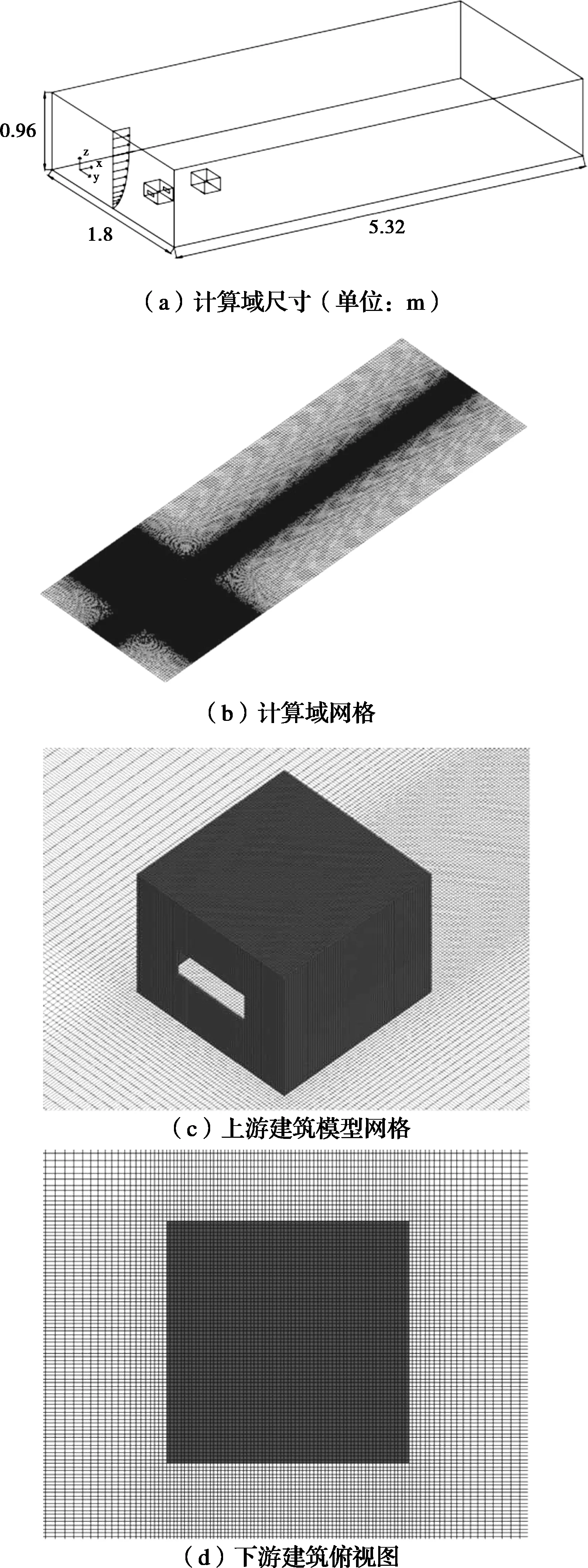
图5 基础网格的计算域及模型

2.2 边界条件设置

在Fluent软件中设置模型边界条件：地面和建筑物表面用自动墙面处理；计算域顶部及侧面的边界条件为Symmetry；出口处设置为Vent-outflow；入口处设置为Velocity-inlet，边界条件编译用由风洞实验所得到的速度曲线与湍流动能曲线编写的UDF。来流边界条件再现风洞实验期间的条件。基于式(1)描述的幂函数分布构造对数入口速度分布。由此产生的对数方程为

(3)

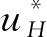
(4)

计算SSTk-ω模型的特定耗散率ω，见式(5)。

(5)

式中：Cμ是等于0.09的经验常数。此部分的参数设置采用Richard等[17]、Gousseau等[18-21]以及Van Hooff等[13]研究中CFD的参数设置。

采用ANSYS中的Fluent软件进行计算，计算模型为5类RANS模型：Standardk-ε模型(标准k-ε模型，下文简称SKE)、Realizablek-ε模型(可实现化k-ε模型，简称RLZ)、RNGk-ε模型(简称RNG)、SSTk-ω模型(简称SST)和RSM湍流模型(简称RSM)。所有控制方程均采用二阶下的有限体积法进行离散化，选用SIMPLE方案耦合压力和速度。采用Intel至强32核心处理器，所有模型的计算时长约为4个月。

2.3 数据处理方法

对实验与模拟所得结果通过式(6)得到各点的平均风压系数。

(6)

式中：CP为各点的平均风压系数；P为总压值；P0为静压值；ρ为空气密度；UH为建筑高度处的气流速度。通过式(7)得到各面的面标准化平均风压系数值。

(7)

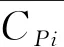
(8)

式中：E为模型模拟结果与实验结果误差。

2.4 与实验结果的对比

上游建筑采用与Van Hooff等[13]完全相同的模型与相似模拟方法，将上游建筑内部模拟气流速度与Tominaga等[11]的实验数据进行对比，得到沿建筑中心平面x/D=0.125、0.5、0.875等7条曲线的无量纲速度(UX/UH)，对比结果如图6所示。将计算结果与文献[13]中相应的结果对比发现，模拟结果与实验结果误差较小，可靠度较高，该模拟方法满足后续研究要求。

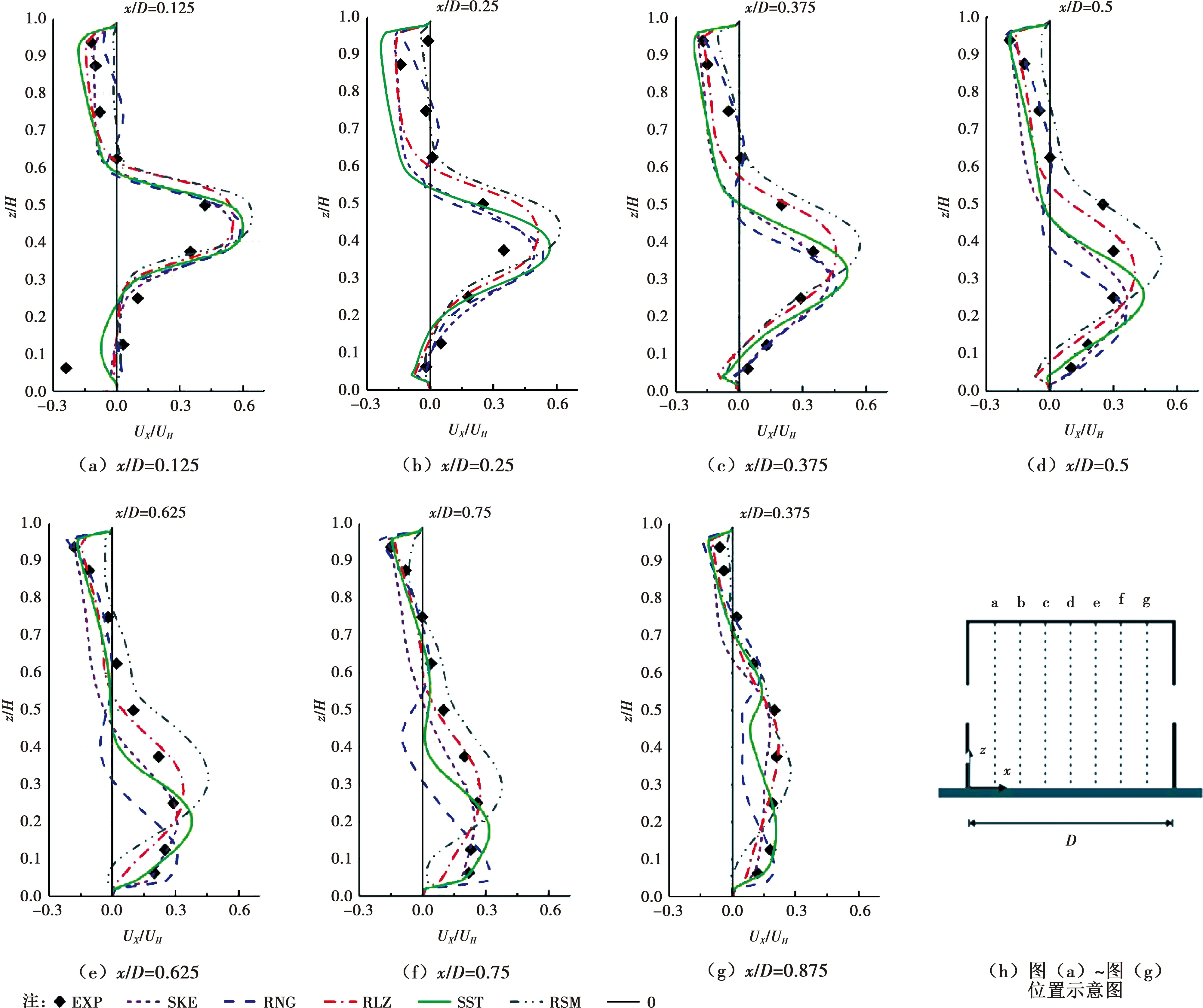
图6 上游建筑内部气流无量纲速度(UX/UH)与实验结果对比

3 网格敏感性分析

计算网格使用Van Hooff等[13]的表面网格技术创建。计算网格仅由长方体网格单元组成，在建筑物及其开口附近加密。为控制总体的网格数，由建筑物到计算域边界进行放大，每个方向的缩放因子r为1.05。网格分辨率采用3种不同的网格密度，这些网格通过精炼和粗化基本网格产生，涉及3种网格密度，对比分析3种网格大小对同一遮挡情形同一模拟模型的影响，模拟对象为上游有孔遮挡的SSTk-ω模型，3种网格密度分别为精细网格(网格密度最大0.02，最小0.002)、基础网格(网格密度最大0.03，最小0.003)与粗化网格(网格密度最大0.04，最小0.004)，对应网格数分别为2 300万、850万与450万。

粗化、基础、精细3种网格都采用SST粘性模型进行对比，图7显示了下游建筑表面的中位背脊线和不同高度腰周线。将不同网格密度模拟结果与风洞实验的结果进行对比，得到有孔遮挡建筑后下游建筑表面的中位背脊线和中位腰周线平均风压系数曲线，如图8所示。3种网格密度模拟平均风压系数相近，变化趋势相同。

修改Roache[22]提出的网格收敛指数(The grid-convergence index，简称GCI)用于估算基础网格在

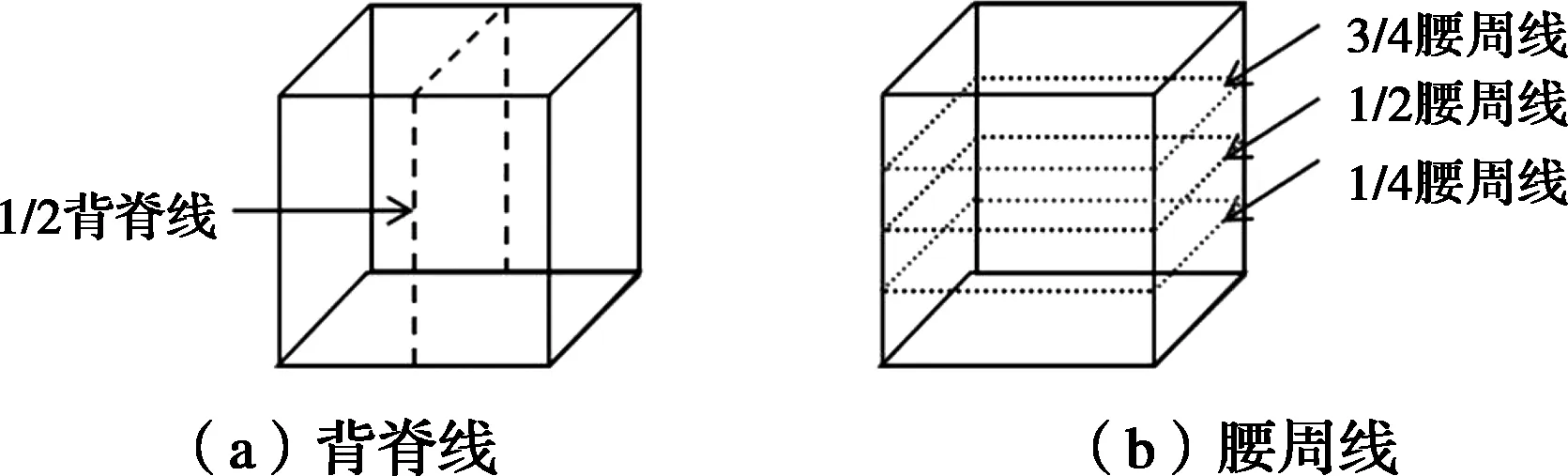
图7 下游建筑背脊线与腰周线示意图

平均风压系数上的误差。

(9)

式中：r为每个方向的缩放因子(r=1.05)，由于采用二阶离散化求解方案模拟，p=2；Fs是安全系数(safety factor)，在分析3种或者更多种网格密度时的推荐值为1.25[22]。沿下游建筑背脊线和腰周线的计算GCI如图9所示，精细网格与基础网格的误差较小，其计算GCI平均值分别为4.0%和5.0%。可得知采用基础网格计算时，模拟结果已经可以满足网格独立要求。在综合考虑时间成本，计算结果收敛性以及满足网格独立等要求后，模拟的最佳网格为基础网格(网格密度最大0.03，最小0.003)，均采用基础网格密度进行计算。

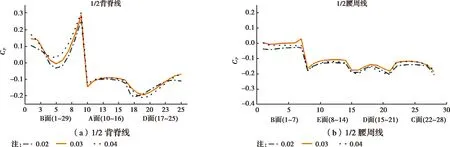
图8 下游建筑1/2背脊线与1/2中腰线平均风压系数

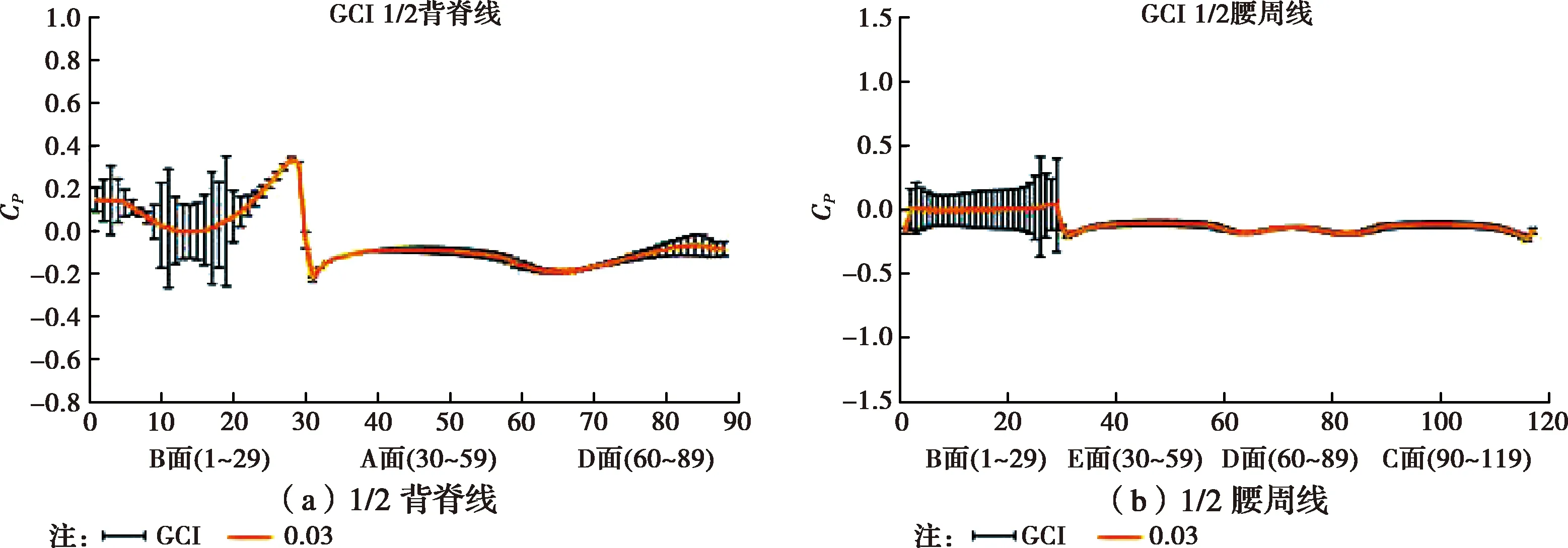
图9 基础网格收敛指数(GCI)

4 CFD模拟结果与风洞实验对比

4.1 上游遮挡建筑有孔情形

研究有孔遮挡时5类RANS模型的可靠性，定义下游建筑顶部为A，迎风面为B，来流风向左侧为C，来流风向右侧为E，下游建筑背风面为D，展开图如图10所示。将模拟结果与风洞实验结果进行比较，得到有孔遮挡时下游建筑表面平均风压系数的中位背脊线及距地1/4、1/2与3/4建筑高度的腰周线，如图11所示。其中,Exp1、Exp2为两次有孔遮挡风洞实验下游建筑表面风压系数。为减少风速对结果的影响，将5类模型的面平均压力系数进行标准化处理，即每个面的风压系数与5个面的平均风压系数的比值(等于下游建筑所有测点平均风压系数)，再与实验值比较，得到的数值误差见表1。表1中Exp1与Exp2分别为上游有孔遮挡风洞实验的第1次与第2次实验平均风压系数标准化数值结果。

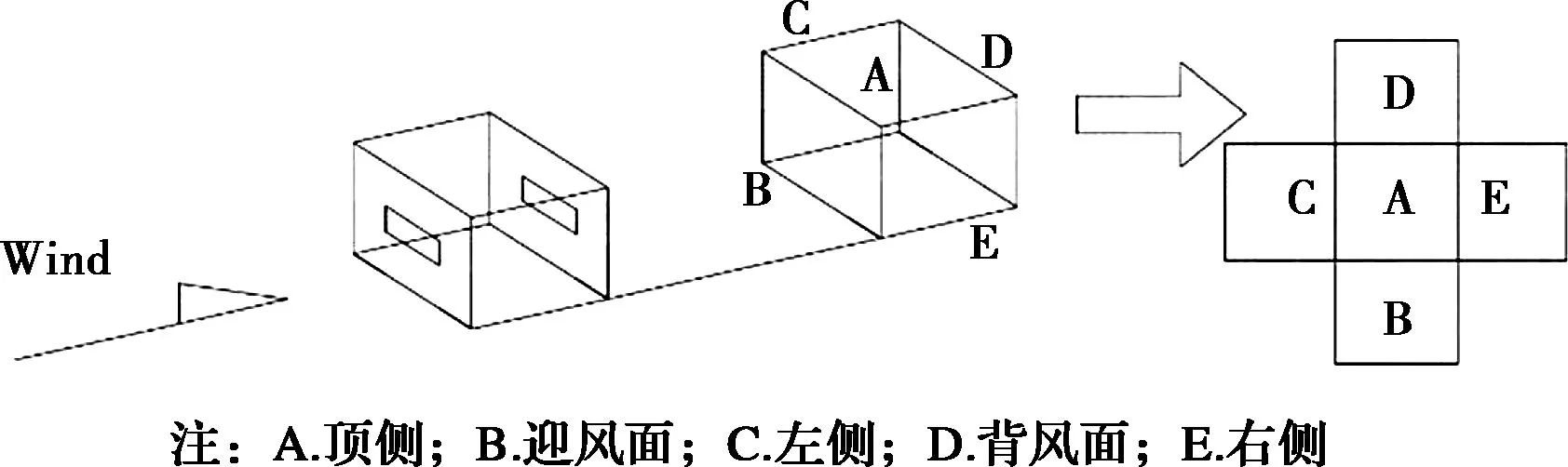
图10 下游建筑展开各面示意图

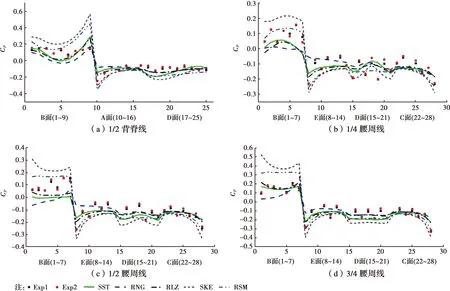
图11 有孔遮挡情形下游建筑背脊线与腰周线平均风压系数对比图

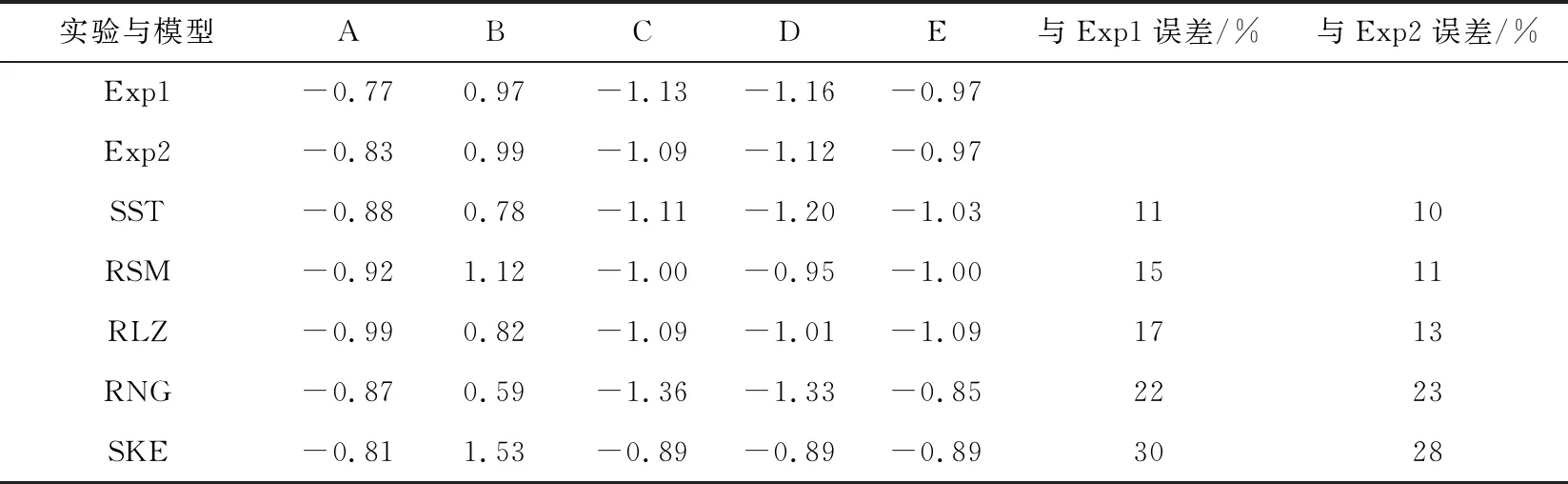
表1 有孔遮挡情形下不同模型标准化数值分析Table 1 Standardized numerical analysis of different models in the case of hole occlusion

对比有孔遮挡的不同模型结果与实验结果可以发现：

1)图11(a)背脊线结果表明，SKE模型在迎风面(1～9号测点)明显高估于实验值，RSM模型在迎风面的高估程度仅次于SKE模型，5类模型在顶面(10～16号测点)与背风面(17～25号测点)结果较于迎风面均拟合较好。

2)由图11(b)、(c)、(d)腰周线可知，SKE模型与RSM模型在迎风面(B面1～7号测点)也存在明显的高估，且SKE模型在下游建筑两侧面(C面22～28号测点和E面8～14号测点)模拟值低估于实验值。

3)图11(b)、(c)、(d)还表明，对于不同位置高度的腰周线，5种RANS模型都显示出建筑上部的模拟结果明显好于建筑下部，这可能是下垫面的粗糙程度对模拟结果存在干扰。

4)图11各图都显示，SST与RLZ模型在背脊线与腰周线各面的拟合程度都高于SKE、RNG、RSM模型。

5)由表1可知，SST模型在数值上表现出高的可靠度(与Exp1和Exp2误差分别为11%、10%)，其次为RSM模型(与Exp1和Exp2误差分别为15%、11%)。

6)由图11和表1可知，SKE模型的模拟可靠性最低，其标准化结果偏差最高为30%。

由此可见，SST模型模拟可靠度最高。

4.2 上游遮挡建筑无孔情形

图12(a)为上游建筑为无孔遮挡时，下游建筑中位背脊线平均风压系数对比图。图12(b)、(c)、(d)分别为下游建筑距地面1/4高度、1/2高度与3/4高度的腰周线风压系数，其中,Exp3、Exp4为2次风洞实验下游建筑平均风压系数。将5类模型面平均压力系数进行标准化处理，得到的数值误差如表2所示。其中Exp3与Exp4为无孔遮挡风洞实验的两次实验平均风压系数标准化数值。

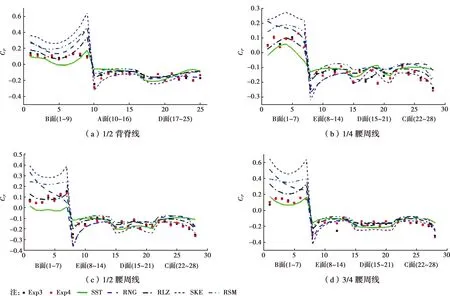
图12 无孔遮挡情形下游建筑背脊线与腰周线平均风压系数对比图

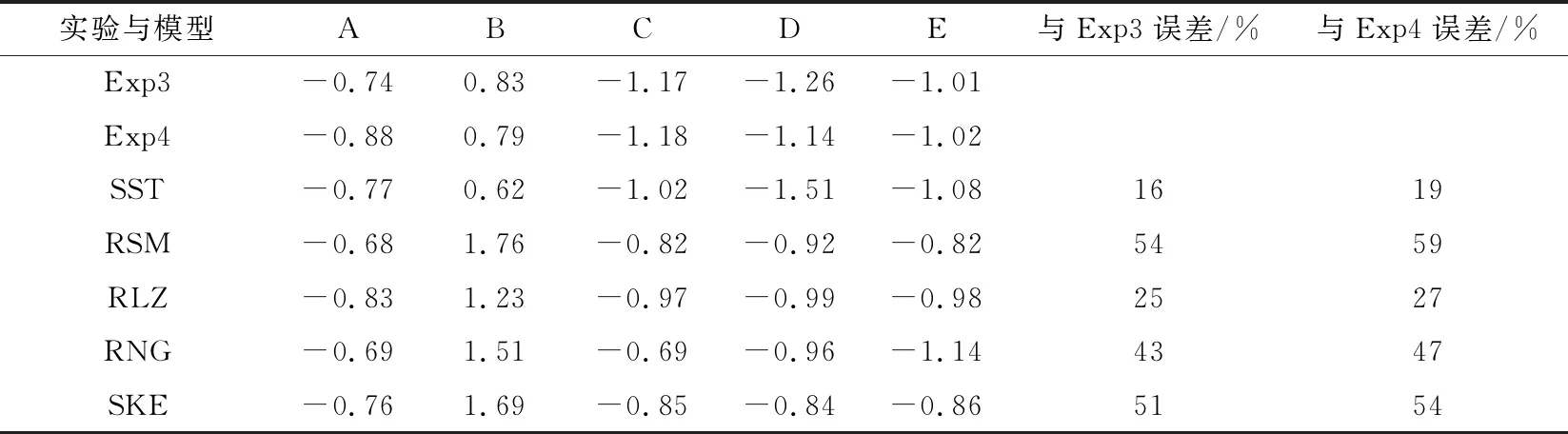
表2 无孔遮挡情形下不同模型标准化数值分析Table 2 Standardized numerical analysis of different models in the case of on hole occlusion

对比无孔遮挡的不同模型背脊线和腰周线计算结果与实验结果可以发现：

1)图12(a)下游建筑表面平均风压系数中位背脊线显示，SKE与RSM模型在迎风面(B面1～9号测点)明显高估于实验值，在顶面(A面10～16号测点)与背风面(D面17～25号测点)5类模型模拟结果均拟合较好。

2)由图(b)、(c)、(d)中的腰周线可知，在迎风面(B面1～7号测点)上，SKE、RSM、RNG模型存在明显高估。总体上SST模型(与Exp3和Exp4误差分别为16%、19%)与RLZ模型(误差分别为25%、27%)拟合最好

3)由表2数据可知，无孔遮挡的RSM模型模拟结果的可靠性最差，与Exp3和Exp4误差分别达54%、59%，其次为SKE模型，与Exp3和Exp4误差分别为51%、54%。

由此可见，SST模型对于无孔遮挡的模拟可靠性最高。

4.3 有孔遮挡与无孔遮挡比较

表1与表2显示同一种RANS模型对于不同遮挡情形的模拟结果偏差不一样。分别比较有孔遮挡与无孔遮挡的5种RANS模型可以发现，RSM模型针对有孔遮挡情形的模拟可靠性结果较好，但对于无孔遮挡情形的模拟结果可靠度最低。表1与表2也表明，无论是有孔遮挡还是无孔遮挡，其模拟结果可靠性最高的都为SST模型。

基于SST模型分别得到两种遮挡情形的中垂面速度矢量图，如图13所示。由图13(a)可知，当上游为封闭建筑，即为无孔遮挡时，气流绕过上游遮挡建筑，在两个建筑间形成一个大的涡旋；由图13(b)可知，当上游为有孔遮挡时，上游建筑的穿堂风会影响建筑间的涡旋，因此，减少上游建筑遮挡的作用，进而流场更接近无遮挡情形，模拟结果更为精确。

将模拟结果进行处理，得到标准化误差表，见表3。由于两次风洞实验值接近，对比结果都取第1次实验结果。由表3平均风压系数标准化后结果可知：有孔遮挡模拟结果相较于无孔遮挡误差约小40%(误差11%与16%的对比)。

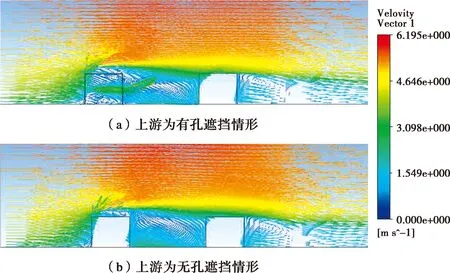
图13 有孔遮挡与无孔遮挡情形下中垂面速度矢量图

表3 有孔遮挡与无孔遮挡SST模型标准化数值分析Table 3 Standardized numerical analysis of SST model with hole occlusion and no hole occlusion

由此可见，SST模型对于有孔遮挡情形好于无孔遮挡情形。

4.4 可视化实验

可视化实验中发烟口位于上游建筑地面中心，发烟试剂采用了15%的丙烯乙二醇溶液，实拍照片如图14所示。可视化实验效果(图14)与SST模型模拟结果(图13(b))有比较好的相似性。

图14与图13(b)都显示，上游建筑的穿堂风在出口处形成冲击气流，破坏了两建筑间的涡旋，在一定程度上减少了建筑遮挡的作用，使得下游建筑更接近于无遮挡的环境。这有可能是有孔遮挡的CFD模拟好于无孔遮挡的原因。

图14 上游有孔遮挡可视化图

5 结论

通过与风洞实验数据的严格对比，分析上游建筑有孔、无孔两种遮挡情形下，下游建筑表面压力CFD模拟可靠性与准确性。通过比较分析3种网格密度及5种RANS模型，得到以下结论：

1)网格敏感性分析显示，当建筑表面的最小网格为建筑高度的约2%时，计算结果满足网格独立性要求。

2)对上游建筑为有孔遮挡或无孔遮挡时，5种常见RANS模型中，SSTk-ω模型的模拟可靠性最高。采用SSTk-ω模型对有孔遮挡与无孔遮挡的模拟对比显示，对前者的模拟误差比后者误差还要低，即上游建筑有孔时，下游建筑表面的风压的数据预测准确性反而更高。这有可能是由于穿过的气流更接近无遮挡的情形造成的。

3)发烟可视化实验显示，有孔遮挡SSTk-ω模型模拟的中垂面气流组织与风洞可视化实验有比较好的相似性。穿堂风气流破坏了建筑间的回流涡旋，削弱了建筑遮挡的效果，使得气流运动更接近无遮挡的情况，这也许是有孔遮挡较无孔遮挡模拟可靠性更高的原因。

采用的CFD设置方法可作为类似风环境模拟的参考方法。只讨论一个风向与一个间距，讨论了稳态RANS模型，而未讨论非稳态RANS模型和LES大涡模拟，这些需要在以后的研究中逐步完成。