轻钢-混凝土混合结构周期折减系数研究
李岐,王志军,b,邓义川,韩立志
(重庆大学 a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆 400045)
低层轻钢结构体系拥有工厂化制作、施工速度快、建筑垃圾少等优势,在很多国家得到了广泛应用。2015年AISI发布的S202-15[1]、S220-15[2]、S230-15[3]、S240-15[4]、S400-15[5],以及2016年NIST发布了Seismic Design of Cold-Formed Steel Lateral Load-Resisting Systems[6]等规范对轻钢结构住宅结构构件和结构的抗震性能给出了全面的技术要求。虽然中国的轻钢结构发展起步较晚,但研究工作在最近十几年也取得了长足进步[7-9],2011年,中国出版了《低层冷弯薄壁型钢房屋建筑技术规程》[10],表明中国低层轻钢结构的发展趋于成熟。
轻钢结构主要应用于低层住宅,这不能适应中国人多地少的国情。为了将轻钢结构体系应用于多高层建筑,笔者提出了轻钢-混凝土混合新型主次结构体系,主结构由“传统”普通混凝土高层结构间隔抽掉2层或3层楼层之后形成,主结构的层高为原普通高层结构层高的2倍或3倍(6~10 m),次结构则为2层或3层轻钢结构,次结构嵌入到主结构中,如图1所示。图1中的“层间连接”是由于楼层梁和楼面板的分隔使得墙体轻钢立柱不贯通所造成的,主要包括抗拔连接件(抗拔螺栓)、腹板加劲件、侧向刚性支撑件等部件[1,10],其中,侧向刚性支撑件对层间连接的刚度影响最大。由于轻钢次结构可以在工厂制作,并可在多个主结构楼层同时进行施工,所以,此类结构体系既能提高预制装配率,又能加快建设速度,同时,由于自重减轻,还有利于提高主体结构抗震能力,减少基础处理难度。
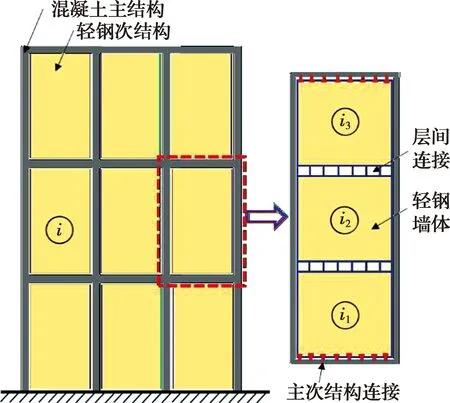
图1 轻钢-混凝土混合结构示意图
为使该新型混合结构应用于工程实际,除了研究混合结构中主、次结构的协同作用外,还需解决此类结构设计中的分析建模问题。轻钢次结构采用轻钢墙体承重,其构造复杂,在设计分析时很难与主体结构一起整体建模,通常只能建立主体结构的简化模型,将轻钢次结构作为“荷载”或“质量”施加在主结构上,也就是将轻钢次结构作为一种特殊“填充墙”来考虑。由于轻钢次结构的刚度对混合结构的刚度有贡献,简化模型没有考虑次结构刚度的影响,使得计算出的周期偏大,如不采用周期折减系数进行折减,一般情况下会导致计算出的地震作用偏小。
一些学者采用试验或有限元分析方法对普通混凝土框架或框架-剪力墙中填充砌体或轻质砌体的周期折减系数做过一些研究[11-15],《高层建筑混凝土结构技术规程》[16]也针对砌体填充墙给出了不同结构体系的周期折减系数取值建议。但轻钢-混凝土混合结构中的2层或3层轻钢次结构有别于砌体填充墙,不能采用已有的折减系数取值。雷阳[17]利用SAP2000计算了轻钢-混凝土混合结构的周期,定性说明了轻钢墙体刚度对混合结构周期的影响,但没有给出具体的周期折减系数计算方法。
有必要对混合结构周期折减系数做进一步研究,提出简化的定量计算方法。笔者首先推导了2层或3层轻钢次结构抗侧刚度,以及轻钢-混凝土混合结构周期折减系数的简化计算公式。在混合框架试验基础上,用ABAQUS有限元软件建立了轻钢-混凝土混合框架的精细化分析模型和简化分析模型。通过有限元模拟分析,验证了提出的轻钢次结构抗侧刚度和混合结构周期折减系数简化计算公式的正确性。
1 简化计算公式推导
轻钢次结构与主结构的连接方式理论上有“侧向连接”和“上下连接”两种,但实际工程中轻钢次结构与主结构混凝土柱或剪力墙的侧向连接较难实现,而采用膨胀螺栓将轻钢墙体与主结构梁连接起来的上下连接则较为方便,故主要针对采用上下连接的主次结构体系进行研究。
1.1 轻钢次结构抗侧刚度简化分析
虽然,聂少锋等[18-19]、石宇[20]和郭鹏等[21]对组合墙体的抗侧性能进行过较深入的研究,并提出了单层冷弯型钢骨架墙体抗侧刚度实用计算公式,但对于轻钢和主结构采用上下连接的混合结构,不能简单依据单层来计算墙体的侧移刚度,而应按照主结构“层”来计算2层或3层轻钢次结构(包括轻钢墙体之间层间连接)的整体侧移刚度。

图2 计算模型示意图
混凝土主结构层间侧移会引起轻钢次结构一同侧移。假定轻钢次结构为3层,每一层轻钢墙体的抗侧刚度为k1、k2、k3,层间连接的抗侧刚度为kc。第3层轻钢墙体顶部和楼板的连接作用简化为一水平作用力F之后,多层轻钢次结构墙体抗侧刚度Ks的计算模型见图2。
第i层轻钢墙体和层间连接产生的位移分别为
(1)
轻钢次结构墙体的顶点位移为
(2)
故
(3)
(4)
同理,当轻钢次结构为2层时,有
(5a)
(5b)
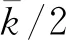
1.2 主结构周期折减系数
当结构的刚度和质量沿高度近似均匀分布时,可以采用顶点位移法近似计算结构的基本自振周期[22]。
假定混凝土主结构第i层(6~10 m层高)的抗侧刚度为Kmi,该主结构楼层内,轻钢次结构的整体抗侧刚度为Ksi,这样轻钢-混凝土高层混合结构对应于第i主结构层的总抗侧刚度则为Kmi+Ksi。
将每一主结构层的自重Gi(包含子结构自重)作为假想水平荷载作用在结构上,考虑子结构刚度贡献的顶点假想水平侧移为
(6)
如果不考虑子结构刚度影响,主结构的顶点假想水平侧移为
(7)
按顶点位移法,考虑和不考虑轻钢次结构侧向刚度影响的混合结构基本自振周期T′和T分别为
(8)
故考虑次结构刚度的周期折减系数为
(9)
假定各楼层结构质量近似一样,有
(10)
2 轻钢-混凝土混合框架的试验及有限元分析
2.1 轻钢-混凝土混合框架抗侧试验研究
2.1.1 试验简介 为了研究混合结构中轻钢次结构的刚度贡献,以及为有限元模拟提供试验依据,进行了轻钢-混凝土混合框架抗侧试验,3个代表性试件的参数见表1。试件SY1为纯混凝土主框架,试件SY2为轻钢-混凝土混合框架,试件SY3为单层轻钢次结构墙体试件。

表1 试件参数
试件SY1和SY2的混凝土主框架尺寸和配筋完全相同,详见图3。混凝土设计强度等级为C30。2层轻钢次结构墙体的构造见图4,墙体轻钢龙骨架材料采用S550的C型冷弯薄壁型钢,规格为C89×37×7.5×0.8,组合墙体面板采用18 mm厚OSB板单面覆板,用自攻螺钉将OSB板与墙体轻钢骨架连接,自攻螺钉的外周间距为150 mm,内部间距为300 mm。
SY2试件采用膨胀螺栓将2层轻钢组合墙体的上部和下部分别与混凝土主框架和地梁相连,形成轻钢-混凝土混合框架结构。在次结构第1层和第2层之间,采用4块尺寸为400 mm×200 mm的OSB板(上下各5颗自攻螺钉与轻钢墙体连接)来模拟次结构的层间侧向连接,见图4(b)。
3个试件均采用顶点水平加载,加载装置如图5所示。为了防止试件SY3过早平面外失稳,在试件两侧中上部设置了侧向支撑(见图5(b))。低周往复加载采用位移控制,每级位移为1/500层间位移角的倍数,循环两次,直到试件破坏。单层轻钢组合墙体也按1/500层间位移角的倍数来进行位移控制单调加载。
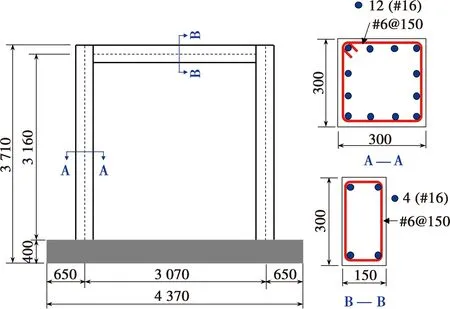
图3 框架几何尺寸及配箍图

图4 2层轻钢墙体

图5 试验构件加载装置
试验中在试件顶部左右两侧安装拉杆式动态位移计来测量试件顶点侧移,同时,在地梁左侧安装位移计来监测试件滑移。在框架梁左右两端300 mm范围上下纵筋及框架柱柱脚300 mm范围左右纵筋贴钢筋应变片来监控梁柱纵筋应力大小。
钢材和OSB板性能如表2所示。实测混凝土立方体试块抗压强度平均值为43.6 MPa。

表2 钢材和OSB板力学性能Table 2 Steeland OSB mechanical properties
2.1.2 试验结果 试件SY1在加载到层间位移角1/500时,梁左右两端截面受拉处出现0.1 mm左右的弯曲裂缝,随后在柱脚受拉处也出现细小弯曲裂缝。当位移加载到1/100层间位移角时,梁端纵筋钢筋受拉屈服形成塑性铰,梁端最大裂缝宽度已大于0.2 mm,同时,在梁柱节点区出现了第1条斜裂缝。位移继续增大时,梁端、节点区和柱脚裂缝越来越多,如图6(a)和图6(b)所示。当正向层间位移角约1/40时,达到最大水平荷载130 kN,梁端混凝土开始掉渣。加载到层间位移角约1/33时,水平荷载略有减小(约128 kN),因水平侧移较大便停止了继续加载。

图6 试验现象
试件SY2混凝土框架上裂缝的发展过程和SY1基本相同,但框架梁上纵筋受拉屈服要略晚于SY1(约在1/86位移角)。相同层间侧移时,试件SY2所施加的水平荷载要大于试件SY1,说明轻钢次结构参与了协同受力。在层间位移角小于1/166时,次结构组合墙体上OSB板和层间楼盖梁均无明显变形。随着侧向位移增大,轻钢组合墙体发生抖动和响声,墙体相邻OSB板之间发生错动,OSB板竖向拼缝发生挤压变形,当层间位移角1/45时,中间OSB板竖向拼缝被局部挤坏,如图6(c)所示。加载至1/33层间位移角时,梁柱节点处和梁端混凝土开始掉渣,停止试验。SY2的正、反向承载力比SY1有较明显的增加,特别是正向承载力增加幅度更大,由130 kN增大到171.3 kN。
试件SY3加载前期力-位移曲线基本保持直线,约1/300层间位移角之后,力-位移曲线发生弯折,加载过程中,轻钢墙体龙骨发生抖动和响声,相邻OSB板之间的竖向拼缝发生错动,虽然设置了侧向支撑,但当侧向位移达到22 mm(约1/73位移角)时,构件发生明显扭转,试验中止。
试件SY1-SY2的滞回曲线如图7所示;试件SY1和SY2的骨架曲线如图8所示,试件SY3的推覆力-位移曲线如图9所示。
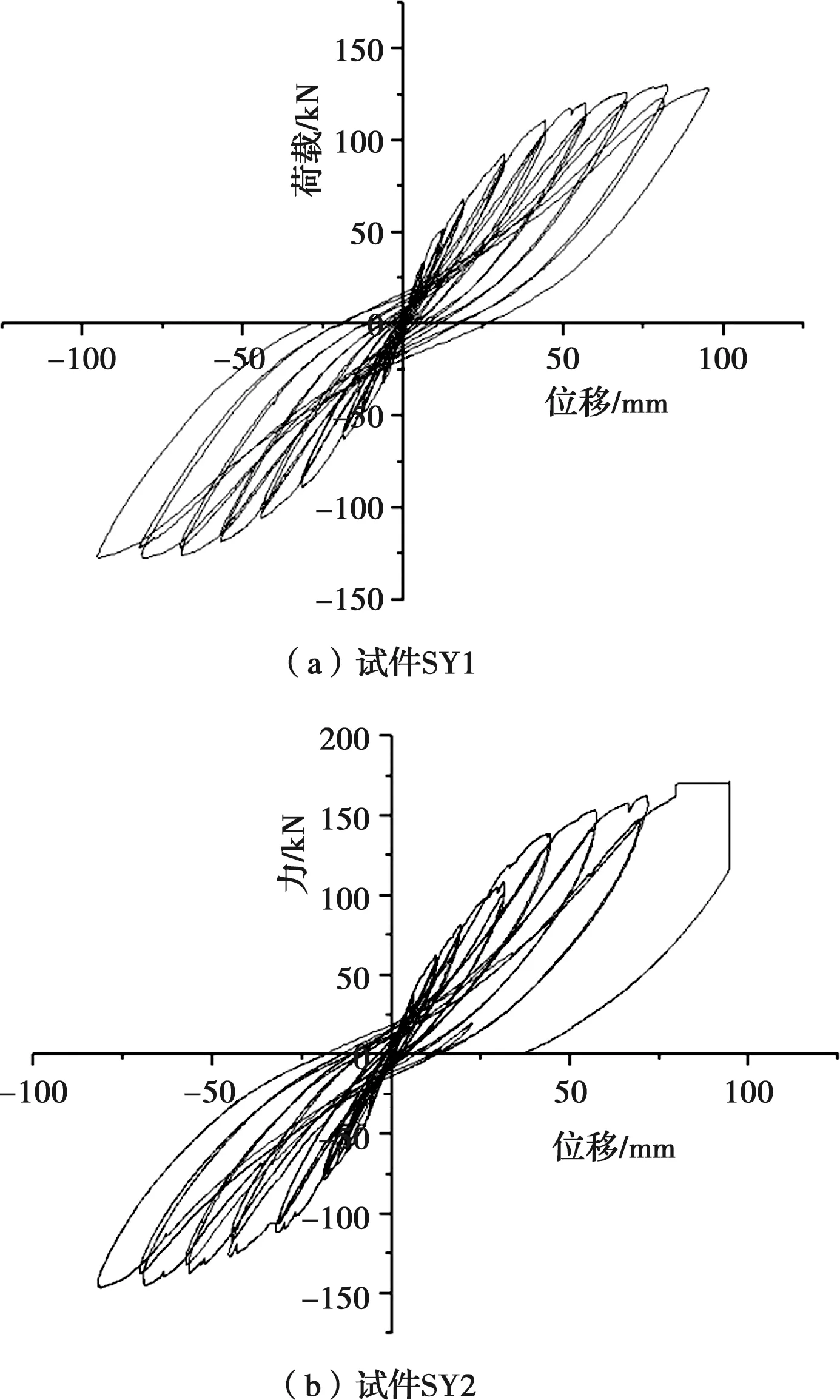
图7 试件SY1和SY2滞回曲线

图8 试件SY1和SY2骨架曲线

图9 试件SY3推覆力-位移曲线
2.2 轻钢-混凝土混合框架精细化有限元分析
2.2.1 有限元模型建立 用ABAQUS软件对轻钢-混凝土混合框架进行精细化有限元分析。混合框架由钢筋混凝土框架和轻钢-OSB板组合墙体两部分组成。混合框架的精细化建模涉及到钢筋混凝土框架、轻钢-OSB板组合墙体以及它们之间连接的模拟。
针对混凝土框架的ABAQUS非线性有限元分析相对比较成熟,其中,具有代表性的是清华大学潘鹏开发的PQ-Fiber[23]材料本构模型,该模型能较好地模拟钢筋混凝土框架的滞回性能。在ABAQUS中采用三维纤维梁单元(B31)模拟钢筋混凝土框架,钢筋和混凝土材料本构分别采用PQ-Fiber[23]材料本构模型中的Usteel02和Uconcrete02。
轻钢骨架与OSB板之间采用自攻螺钉连接来传递水平剪力,自攻螺钉连接处的挤压剪切滑移对轻钢-OSB板组合墙体的受力性能有较大影响,精细化分析的关键在于自攻螺钉剪切滑移的模拟。如果轻钢骨架与OSB板之间采用“绑定”或“耦合”约束都不能反映这种剪切滑移,故采用弹簧单元来模拟自攻螺钉,在ABAQUS中修改inp文件,通过力与位移之间的非线性改变来模拟出非线性弹簧。螺钉弹簧参数与轻钢龙骨壁厚、OSB板厚度、自攻螺钉距OSB板的端距以及螺钉受力方向有关。自攻螺钉的受力方向分为平行于OSB板长边与垂直于OSB板长边两种情况。弹簧参数根据本课题组所做螺钉双面抗剪试验结果确定,inp文件中输入的弹簧数据如表3所示,表中Fm和δm分别为最大剪力及相应的滑移量,Fy和δy分别为“屈服”时的剪力及相应的滑移量,而δ1和δ2分别对应剪力为0.2Fm和0.4Fm时的滑移量。轻钢龙骨和OSB板采用壳单元模拟,由于已采用非线性弹簧来模拟连接处的非线性变形,故轻钢骨架钢材本构关系采用弹性强化模型,OSB板采用弹塑性模型,材料参数见表3。
对于轻钢次结构和混凝土主结构的上下连接,由于在试验中未观察到膨胀螺栓的明显剪切变形,故采用了刚度较大的线性弹簧来模拟,不考虑剪切滑移。试件SY2的有限元模型如图10所示。

表3 弹簧数据

图10 试件SY2有限元模型
2.2.2 有限元模拟与试验结果对比分析 轻钢-混凝土混合框架中混凝土框架的裂缝分布如图11中的红色部分所示,与试验中裂缝主要分布位置基本一致。

图11 混凝土框架裂缝分布图
试件SY1和SY2的有限元模拟与试验的滞回曲线和骨架曲线比较分别见图12和图13。试件SY1模拟结果和试验结果吻合得更好。试件SY2的正向模拟较好,但反向模拟存在一定的误差,这主要是由于层间C型钢梁存在正、反向变形不一致所造成的。
表4是3个试件模拟和试验正、反向最大荷载的比较,除SY2的反向最大荷载外,其余都吻合较好。

图12 滞回曲线比较

图13 骨架曲线比较

表4 3个试件模拟值与试验值的分析结果对比Table 4 Comparison between simulated and experimental results for 3 specimens
试验与模拟结果的对比分析表明,所建立的精细化分析模型能够较好地反映混合框架的受力性能。
3 轻钢次结构抗侧刚度简化公式验证
由于混合框架中轻钢次结构所受水平剪力在试验中不能直接测出,近似取相同侧移时混合框架SY2和纯框架结构SY1所受水平力之差作为2层次结构所受的水平剪力,次结构的水平力-侧移曲线见图14中的点划线。根据前述分析,如果层间连接侧向刚度足够大,2层轻钢墙体的抗侧刚度可近似取为单层轻钢墙体SY3抗侧刚度的0.5倍,图14中的实线是依据SY3在相同侧移情况下0.5倍试验荷载得到的曲线,从图14中可以看出,2层次结构的刚度小于0.5倍SY3侧移刚度,这主要是由于两方面的原因造成的:一是层间连接的刚度不足够大,二是由于下层(第1层)墙体的转动使得上层(第2层)墙体的实际侧向刚度要小于SY3的侧向刚度。为了说明此问题并验证轻钢次结构刚度公式的正确性,将试件SY2层间连接的4块OSB板减为只设置1块加强OSB板,形成层间连接侧向刚度较弱的新模型SYB。表5和表6分别是SY2和SYB在正向前4级加载时不同侧移处,非线性有限元分析得到的不同部位对应的侧向刚度,Khh和Km分别为混合结构及纯混凝土主结构的侧向刚度,k1和k2分别是第1层和第2层轻钢墙体的侧向刚度,kc是层间连接的侧向刚度。表中Ks是Khh直接减去Km得到的轻钢次结构侧向刚度,Ks1是公式(5a)计算出的侧向刚度。

图14 次结构荷载-侧移曲线
从表5和表6可以看出,轻钢次结构的上层墙体刚度要小于下层墙体刚度;随着层间连接的增强,轻钢次结构的刚度明显增大,同时,混合框架的抗侧刚度也显著增大;简化公式(5a)即使在非线性情况下也有很好的计算精度。

表5 SY2模型刚度对比Table 5 Comparison of stiffness for SY2 model

表6 SYB模型刚度对比
4 周期折减系数简化公式验证
4.1 轻钢次结构的简化模拟
由于轻钢-混凝土混合框架的精细化模型中螺钉数量过多,在建模中需要定义的弹簧单元数量也很大,建模过程繁琐,且每次计算都要在inp文件中定义非线性弹簧的刚度特性,难以广泛应用于多高层结构的分析中,为此,提出简化模拟方法。将轻钢次结构上下层墙体及层间连接直接简化为非线性弹簧,弹簧的力-位移曲线特性可根据试验结果或精细化模拟得到,例如,试件SY2的简化模型如图15所示。

图15 试件SY2简化模型
简化模型得到的混合框架骨架曲线与精细化模拟的结果对比如图16所示。由图16可以看出,简化模拟与精细化模拟的结果非常接近,完全可用于较复杂的结构进行整体分析。

图16 简化模拟与精细化模拟对比
4.2 简化公式验证
用简化模型方法来验证某10层混合框架结构的周期折减系数。该10层混合框架的主结构框架为3跨5层,每一主结构层中有2层轻钢次结构。主结构梁混凝土强度C30,柱混凝土强度等级见表6。主结构柱截面700 mm×700 mm,梁截面300 mm×700 mm,其边跨跨度8 400 mm,中跨跨度8 100 mm,层高7 400 mm,主结构各层弹性刚度和附加质量见表7。

表7 主结构各层刚度和质量Table 7 Stiffness and mass of the main structure
由于是计算基本周期,用线弹性弹簧来模拟轻钢墙体,每层轻钢墙体的弹性刚度由文献[21]中的简化公式计算得到,边跨2 200 N/mm,中跨1 578 N/mm。轻钢层间连接刚度取决于侧向刚性支撑件设置数量,笔者对设置不同层间连接部件的层间连接试件进行了大量试验研究(另文介绍),试验结果表明,设置不同构造的刚性支撑件后,层间连接刚度大约是轻钢墙体侧向刚度的1~4倍,为了说明层间侧向连接刚度对混合结构周期的影响,层间连接弹簧刚度按表8取了3种情况,分别为边跨墙体侧向刚度的4倍、2倍和1倍。采用简化模拟方法建立的混合框架的有限元模型如图17所示。有限元计算出的混合结构周期、主结构周期、折减系数χT及简化式(9)、式(10)计算所得周期折减系数分别为χT1和χT2,相应的误差见表8。

图17 混合框架简化模型
由表8可以看出,随着层间连接刚度的减小,轻钢次结构的刚度随之减小,周期折减系数逐渐增大。式(9)和式(10)计算的周期折减系数与有限元结果都非常接近,即使在质量不均匀情况下,式(10)计算的误差也在0.5%以内,说明提出的周期折减系数简化公式具有一定的准确性。

表8 周期折减系数对照Table 8 Comparison of the period reduction factors
5 结论
1)考虑轻钢层间连接的侧向刚度,建立了2层或3层轻钢次结构墙体的抗侧刚度简化公式。
2)采用顶点位移法,推导了轻钢-混凝土混合结构周期折减系数简化计算公式,给出了定量计算周期折减系数的方法。
3)根据混合框架试验结果,建立了轻钢-混凝土混合框架的精细化模拟方法和简化分析方法,试验结果和模拟分析结果吻合较好。
4)依据数值分析结果,验证了提出的轻钢次结构抗侧刚度以及混合结构周期折减系数简化公式的准确性。

