基于多注释器标注下的标签排序学习方法
陈华烨 汪海涛 姜 瑛 陈 星
(昆明理工大学信息工程与自动化学院 云南 昆明 650500)
0 引 言
近年来,排序学习作为计算机领域内相对较新的研究课题迅速发展。在许多计算机应用中扮演着重要的角色,例如信息检索、数据挖掘、自然语言处理和语音识别等应用[1]。在有关排序学习的研究中,实例是一组对象,标签是在实例上应用的排序。通常每个标签都假定为客观且可靠的,可用于其他常规监督设置,例如分类[2]。但在现实世界的任务中,生成准确的训练标签是很难实现的,或者代价太高。
对于标签的生成,现有的解决方法是让各种专家或注释器提供多个(可能是主观的或嘈杂的)标签[3]。例如,AMT(Amazon Mechanical Turk)允许任务发布者雇拥来自世界各地的工作者执行众包式数据标注。任何AMT工作者都可以根据自己的选择来完成标签任务。因此,这使得AMT任务发布者可以轻松快速地雇佣多个标注者。由于AMT工作者在进行标签任务时有一定的主观性,所以无法保证客观准确的标签。因此,可以基于多个注释器进行研究学习。目前研究的列表排序学习算法涉及多个注释器。此外,将有关注释器的专业知识的信息作为辅助信息,例如:注释器的信用评分、专业成绩、历史注释记录等[4],运用在标注任务中,作为排序函数的约束函数,得到更精确的标签。
本文尝试了一种新的标签排序方法,结合了两个经典的概率排序模型[5],即Mallows模型和Plackett-Luce(P-L)模型。在这个新提出的排序模型中,要学习排序函数、真值标签、注释器的专业知识程度的参数,以及关于注释器的专业知识与其相关辅助信息的自然整合。随后,列表排序学习的具体算法根据所提出的条件,加入带有注释器的辅助信息,进行概率排序。在每个学习算法中,使用最大似然估计方法,并且引入新的期望最大化(EM)程序迭代更新真值标签、专业知识程度的参数以及要学习的排序函数的参数[6]。具体技术思路如图1所示。
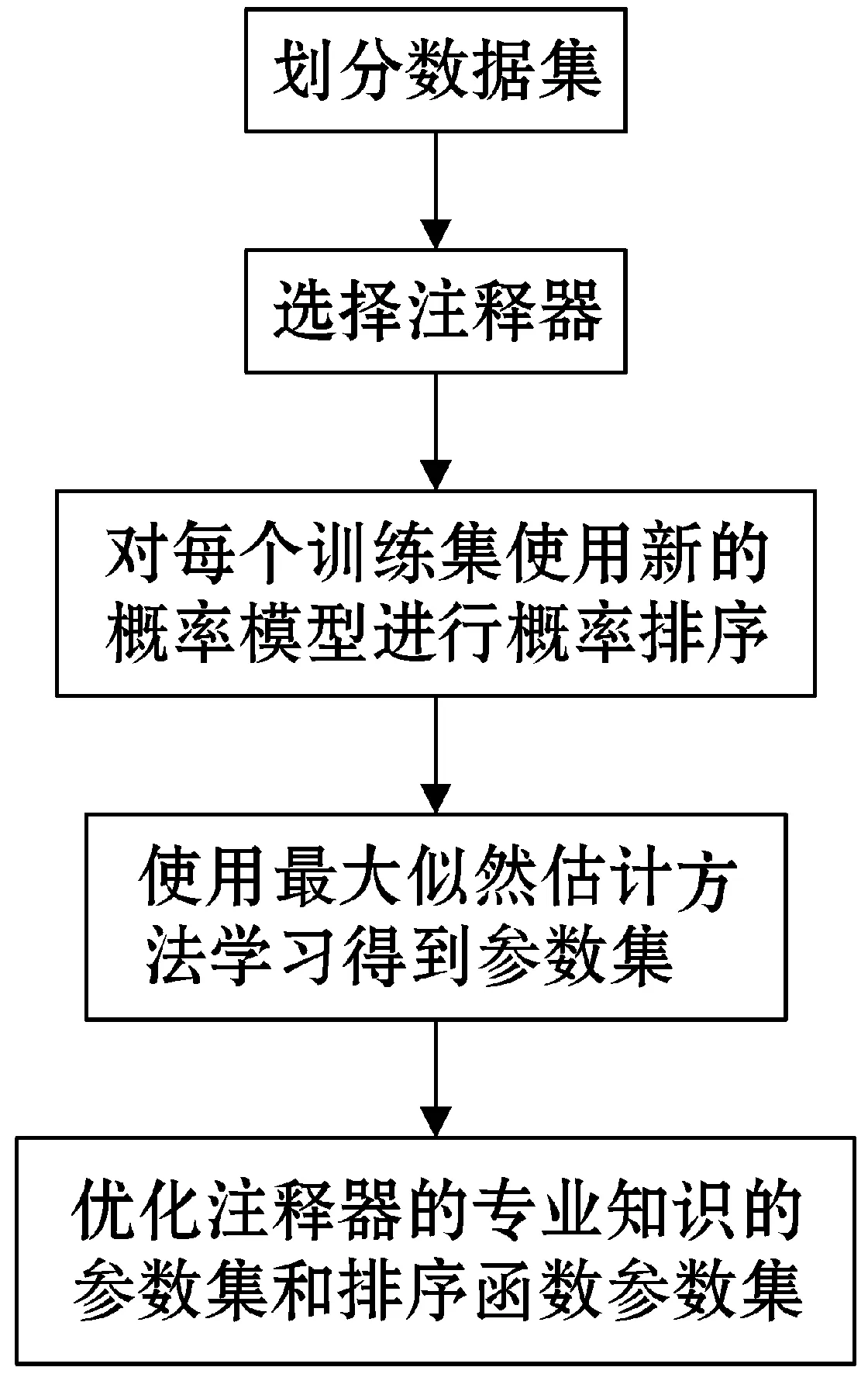
图1 技术思路
1 基于概率排序模型的标签排序学习算法
1.1 Mallows模型
Mallows模型是Mallows在20世纪50年代首次引入的基于距离的概率模型,标准的Mallows模型是属于指数族的双参数模型[8]:
(1)
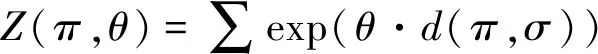
(2)
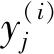
(3)
对于归一化常数Z:
(4)
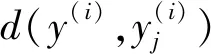
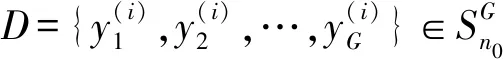
(5)
式中:Θ为注释器的专业知识程度的参数集,Θ={θ1,θ2,…,θG}∈RG,P(y(i))是先验的。
(6)
Mallows模型属于等级聚合模型,该聚合将许多观察到的不同排名列表,组合在同一组成员上,以推断出“更好的”排名。所以Mallows模型可以直接扩展到聚合排名中。如果式(5)中的距离是右不变的[9],则实现如下表达:
(7)
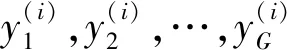
1.2 Plackett-Luce模型

(8)
Mallows模型和P-L模型之间的区别在于前者指的是排序之间的关系,而后者指的是单个排序的概率。
2 列表排序学习
排序学习研究可以分为三类,即逐点、成对和列表[1]。本文通过列表排序学习来定义关于真值标签排序和预测标签排序的损失函数,并根据训练损失最小化来学习排序函数的参数。将所有训练集的可能性损失之和最小化,似然损失函数定义如下:
l(〈w,x〉〗=wTx,y)=-logP(y|x,w)
(9)
式中:〈w,x〉=wTx=f(x)是具有线性特征的排序函数,P(y|x,w)可以通过P-L模型计算。给定训练实例x(i)∈X,X为输入空间,其元素为实例,假设真值标签y(i)∈Y存在,Y为输出空间,其元素是X中实例的排名标签,构造两者之间的关系:
(10)
式中:w∈Rnf×1是排序函数的参数向量,nx(i)是实例x(i)中的对象数,l、k是计数变量。
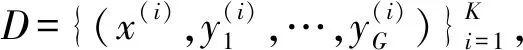
这种目标可以直接通过两个阶段策略来实现。应用Mallows模型将注释器提供的排序标签融合在一起,以估计注释器的真实值和专业程度;基于估计的真值标签训练排序函数,使用常规排序学习算法来训练。将这种方法称为Method1。但这种直接的方法并不稳健,因为如果第一阶段估计的真值不好,第二阶段就会失败。所以,可以将这两个阶段整合为一体。
3 一种新的概率排序学习模型
3.1 模型提出
给出一种新的概率排序学习模型,该生成过程可以通过图2描述。设真值标签排序y(i)由v(=〈w,x〉)调节,其中v(v>0)是标签分数的参数化,y(i)的值现在从先前P(y|v)中抽取,实现了以下表达:
(11)
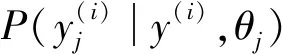
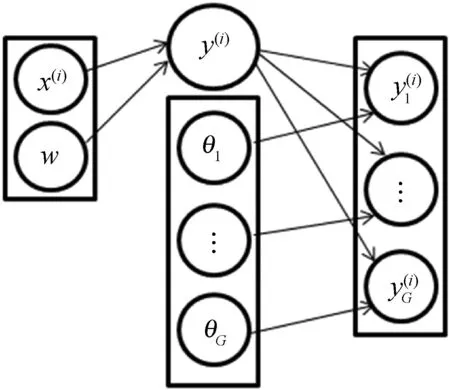
图2 概率排序模型
3.2 最大似然估计方法
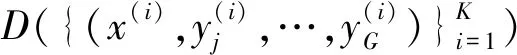
设Ω=(w,Θ)是基于观测集D的参数的似然函数:
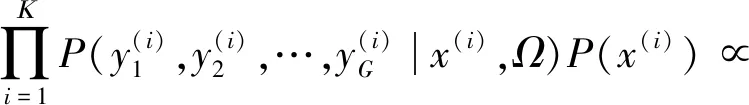
P(y(i)|x(i),w)]
(12)
(13)

参数θ表示注释器的专业知识程度,在此将引入注释器的辅助信息,这些辅助信息可以预先获得[12],在数学上,辅助信息可以描述为:
θj≤θh
(14)
式(14)表示第j个注释器比第h个注释器更专业,标注的准确度越高。将注释器的辅助信息代入式(13),即:
(15)
s.t.θj≤θh,j,h∈[1,2,…,G]
在此考虑一个特殊情况:存在一个注释器具有比其他所有注释器更高的专业程度。 在不失一般性的情况下,假设第一个注释器具有最高的专业程度。在此情况下,式(15)可以变为:
(16)
s.t.θ1≤θh,h∈[2,3,…,G]
将式(15)中的约束由S形函数代替:
(17)
式中:η(≥0)表示辅助信息的置信度。若置信度趋于零,则辅助信息失效。若置信度区域正无穷,则置信度相当高,并且可以满足辅助信息。如果给出置信度,则需等式(15)进行改进,以便通过最大化对数似然来获得最大似然估计量,即:
(18)
在此将基于注释器辅助信息的排序学习算法称为Method3。
3.3 方法推理
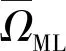
(19)
式中:y={y(1),y(2),…,y(K)}。
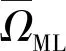
E-步骤:该过程计算观测集D和真值标签y(i)相对于观测集D和从中获得的估计参数集Ω′的对数似然的期望值(E(·)):
Q(Ω,Ω′)=Q(w,Θ;w′,Θ′)=
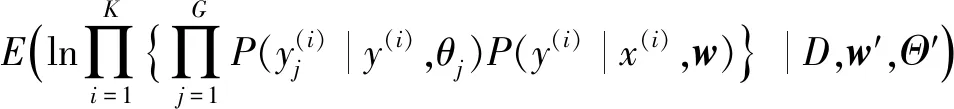
(20)
根据Method3中注释器的辅助信息的加入,相应的E-步骤为:
Q(Ω,Ω′)=Q(w,Θ;w′,Θ′)=
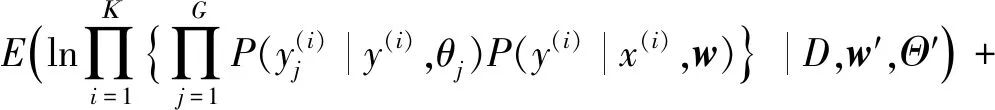
lnfη(θ)
为此使用以下引理:
引理1
Q(Ω,Ω(t))=Q(w,Θ;w(t),Θ(t))=
(21)
式中:
(22)
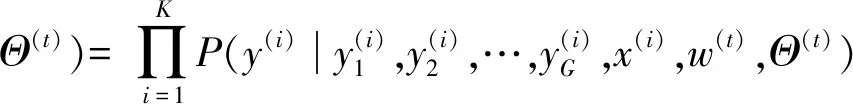
(23)
M-步骤:通过解决式(21)的最大化问题来更新参数集。
引理2对于任何w,通过Θ=(θ1,θ2,…,θG)实现Q乘以Θ的最大化,即:
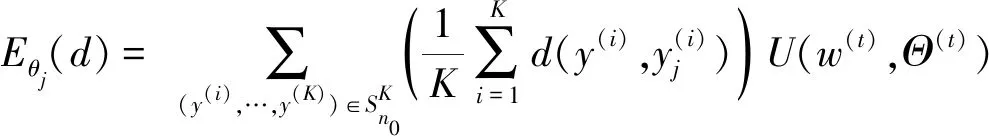
(24)
引理3对于任何Θ,Q乘以w的最大值等于交叉熵CE(Cross Entropy),其公式如下:
(25)
证明:
Q(w,Θ;w(t),Θ(t))=
λ(w(t),Θ(t),Θ)
(26)
在EM的每次迭代中,通过求解式(24)来更新Θ,同时通过最小化式(25)来更新w。 在式(24)中,Eθj(d)是:
(27)
在实践中,计算式(24)比较困难。本文采用抽样方法来获得式(24)右边的近似解。通过二分搜索法获得Θ,步骤如算法1所示。
算法1更新Θ
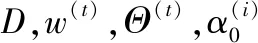
输出:Θ(t+1)
步骤
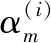
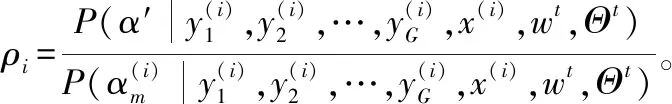
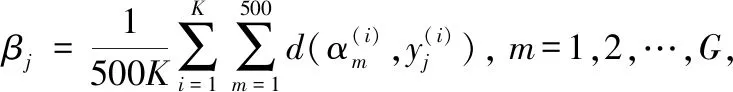
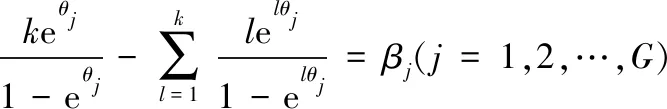
使用最大化对数似然估计更新w,算法2的步骤如下:
算法2更新w,Θ
输入:D,w(0),Θ(0),ε1,ε2
输出:w,Θ
步骤
1. 使用算法1计算Θ(t+1)。
2. 在算法1中重复采样步骤1和步骤2,以获得每个实例的排序集。
3. 从采样集中为每个实例选择最大元素。这些最大元素是该特定迭代的估计真值排序。
4. 使用最大化似然估计更新w与估计的真值标签。
5. 如果t<150,或‖Θ(t)-Θ(t+1)‖<ε1并且‖w(t)-w(t+1)‖<ε2,返回w(t+1)和Θ(t+1); 否则t=t+1,转到步骤1。
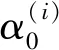
4 实 验
4.1 实验准备
实验采用OHSUMED测试数据集,将此数据集作为排序学习的基准集[13]。此数据语料库有106个查询,每个查询数据由查询-文档对组成,每对都有45维特征,并在其上进行相关性判断。相关程度分为:强相关、弱相关和不相关。将提出的三种方法在训练集和测试集上实现,以训练出最佳参数。提出的新模型用于对测试数据进行排序。最后,将实验通过评估标准作为对比,使用的评估标准:平均精度(MAP)和归一化折现累积增益(NDCG),记录每个方法的评估结果。实验中它们的评估值越高,结果越好。
此实验在完全排序中使用本文提出的三种方法进行评估。在每个实验中,将算法2中的ε1和ε2分别设置为0.01×G和0.01×n,n=45是特征维度;w(0)的每个条目设置为1/n;Θ(0)随机初始化;在Method3中的参数η设置为20;注释器G∈[5,10]。
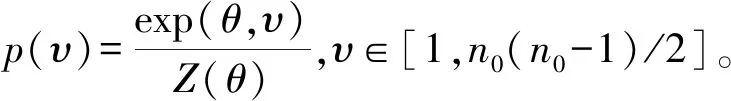
4.2 实验结果及分析
根据实验结果,图3分别显示了Method1和Method2在OHSUMED数据集上NDCG@3和NDCG@5的性能结果。提出的方法Method2的性能在大多数G值上明显优于Method1,由此可以看出,本文提出的方法明显优于常规排序学习算法,其方法统一了真值估计和模型学习。我们还注意到在图4中显示了MAP的结果,Method2比Method1对注释器数量的变化更强,部分原因是在Method1中,模型学习在第一步对真值估计非常敏感,而在Method2中,模型学习可以在下一次迭代中的反馈值代入到真值估计。所以由此可见Method2比常规排序学习算法Method1更稳健。图5显示了在NDCG@5中模拟了根据注释器的辅助信息估计专业知识程度的结果,在大多数G值上Method3略好于Method2,都优于Method1。通过利用辅助信息所提出的算法,提高排序学习能力。
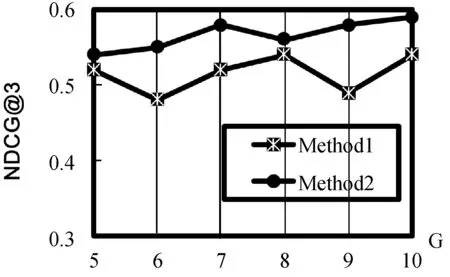
(a) NDCG@3
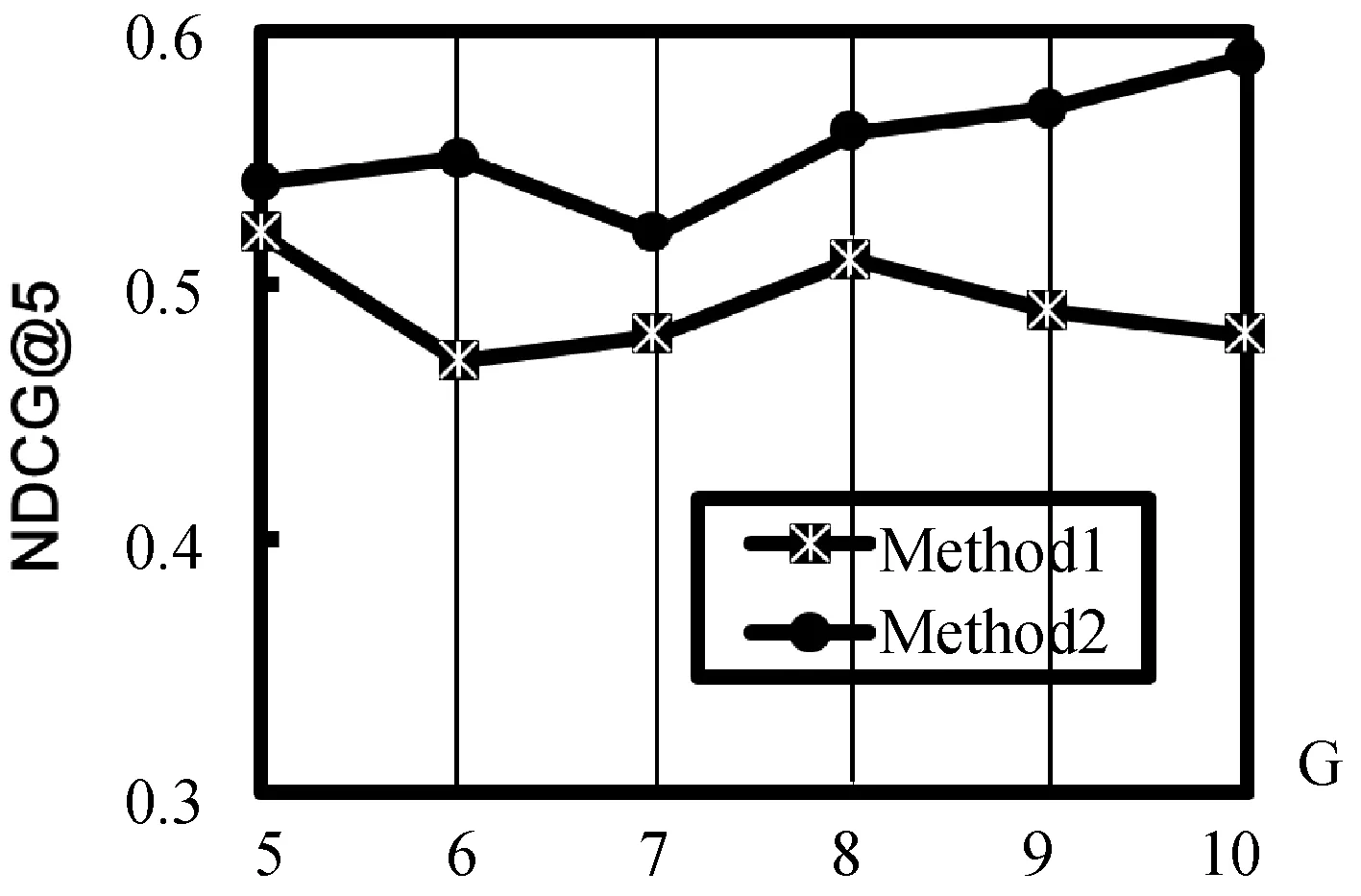
(b) NDCG@5图3 Method1和Method2在OHSUMED数据集上 的性能比较
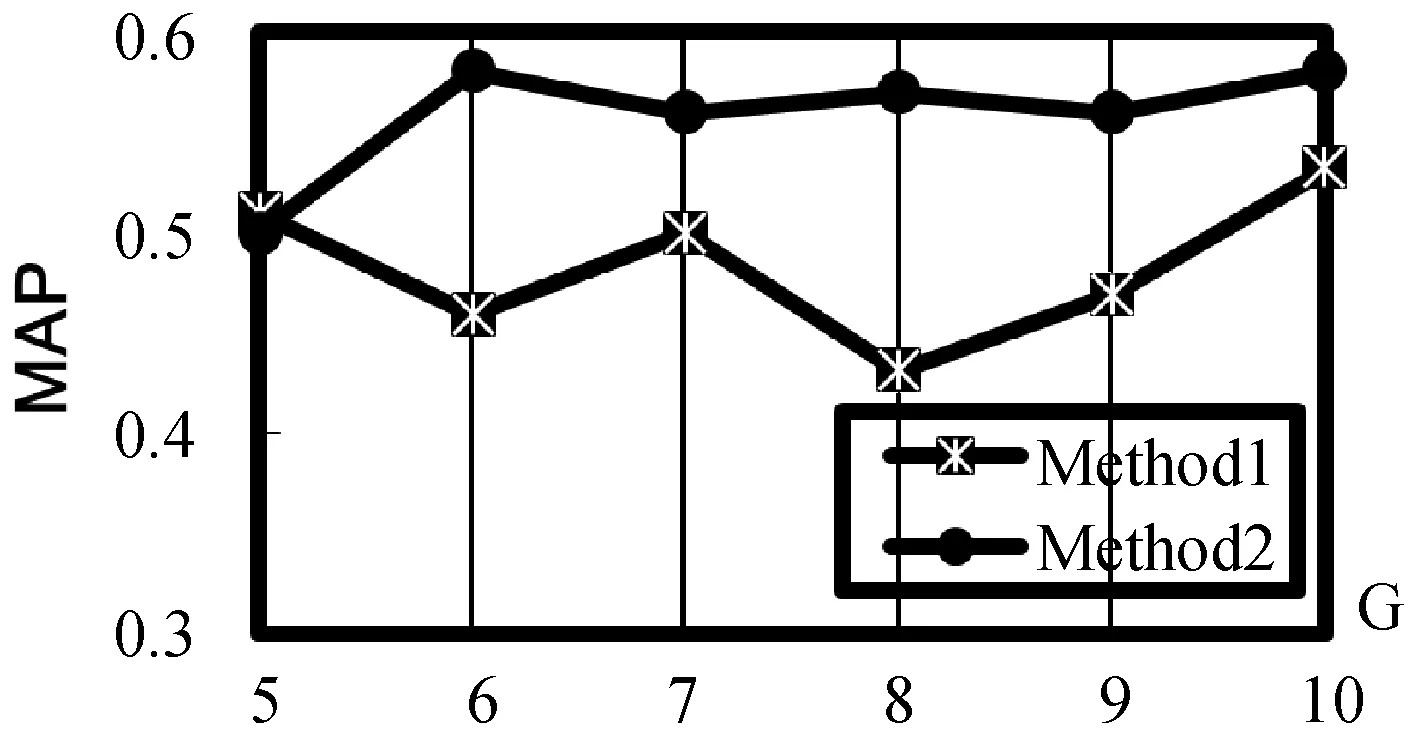
图4 OHSUMED数据集的性能(MAP)比较
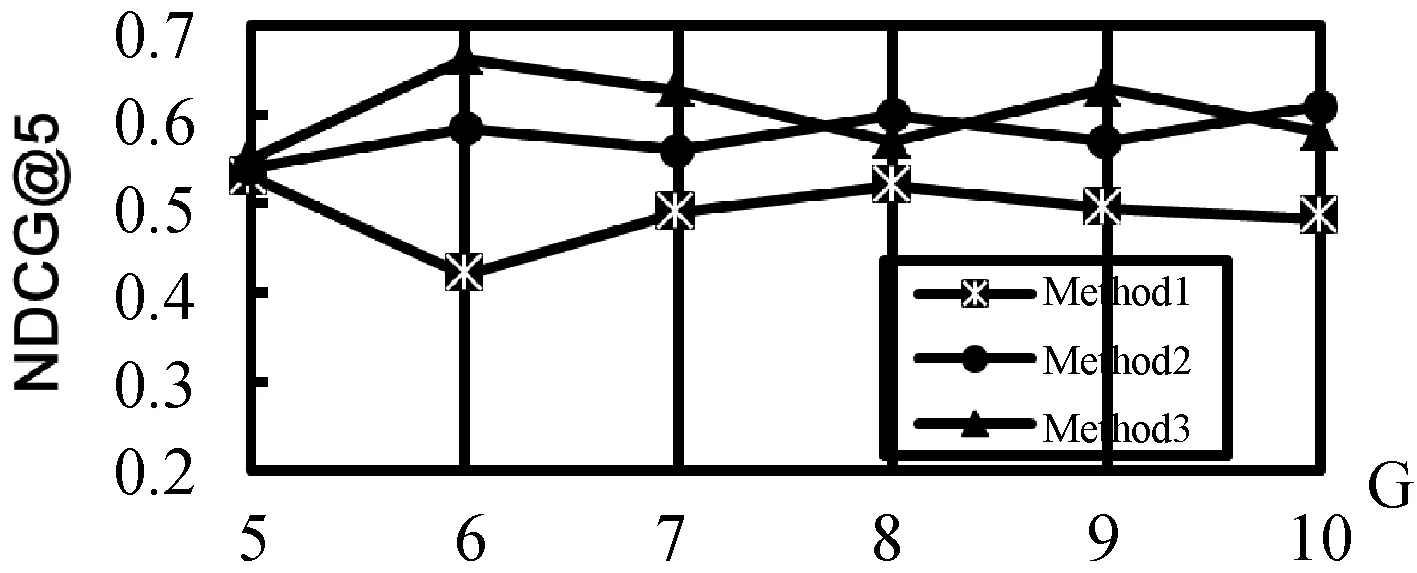
图5 三种方法在OHSUMED数据集上的性能比较
为了比较所涉及方法的收敛速度,在每次EM迭代结束时,我们根据每个EM迭代为每个算法定义的概率选择最佳排序样本,并计算所选最佳排序样本与真值排序标签之间的平均Kendall-Tau距离。图6为三种算法在每次EM迭代时所选择的最佳排序样本与真值排序标签之间的(平均)Kendall-Tau距离(d)的收敛。图中Method3的收敛速度比算法Method2快得多,由此可以得出,Method3中的辅助信息可以降低优化过程的计算复杂度,Method1的收敛性明显差了很多。
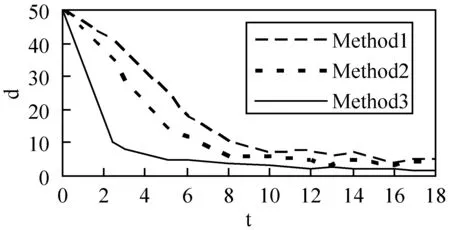
图6 三种算法在Kendall-Tau距离方面的收敛性
5 结 语
本文研究了在多个注释器下进行标签排序的学习,这些注释器提供的标签不是绝对准确的。通过将Mallows模型和P-L模型结合作为概率排序模型中的新学习模型,对测试数据进行排序。提出了新的学习方法对排序模型进行参数估计,Method2迭代地估计真值标签,使用传统算法来训练基于真值标签的排序函数,将真值标签和排序函数与最大似然估计框架结合。在许多众包标签任务中可获得关于注释器的辅助信息(例如,信用记录、专业等级和注释准确性的历史)。因此,提出方法Method3,此方法在Method2的基础上加入注释器的辅助信息。实验结果表明,方法Method2优于直接方法Method1,在考虑辅助信息的情况下,算法Method3同样可以获得比算法Method1更好的结果。如果将一些真实标签注入训练集,则可以进一步提高性能。并且通过Method3的实验结果可知,注释器的辅助信息有助于提高标签的准确性,降低学习优化过程中的计算复杂度。

