基于粒子滤波的智能机器人定位算法

章弘凯 陈年生 范光宇

(上海电机学院电子信息学院 上海 201306)

0 引 言

定位技术是智能机器人领域的研究热点与难点之一。轮式智能机器人在运动过程中，通过自身携带的里程计、激光雷达、摄像机等传感器数据，获得周围的环境信息。通过这些信息和一定的定位算法，实现机器人自身位姿的估计，达到定位的目的。

经过多年的研究，很多学者或技术人员，提出了各种移动机器人的定位方法。文献[1]首次提出了移动机器人的蒙特卡罗定位(MCL)，以一定数量的粒子去估计机器人位姿的后验概率分布。此算法可以较好地近似机器人位姿概率分布，但是采样样本粒子数固定。当机器人能较好估计出位姿时，仍然需要大量的粒子来估计位姿，计算量大，实时性差。为了解决计算量大的问题，文献[2]引入了具有自适应样本集的KLD(Kullback-Leibler Divergence)采样，即粒子滤波的自适应采样，可以随时间改变粒子采样数目，显著降低粒子采样所需的样本数量，但系统鲁棒性较差。文献[3]在粒子滤波重采样阶段引入自适应重采样，显著降低了重采样阶段的计算量。文献[4]在粒子滤波的基础上提出直方图滤波算法(HF),该算法定位精度较高，但是鲁棒性较差。在环境中由于动态障碍物的影响，定位容易出现错误，在初始位姿有偏差的情况下，定位精度存在较大误差。文献[5]提出了在基于EKF算法的框架下，融合多种传感器的数据，适用于大范围的小车定位导航，稳定性高，但是实时性较差。文献[6]提出在基于AMCL算法下，利用高斯-牛顿法将激光雷达点云与栅格地图从粗到细进行匹配，并且利用激光雷达数据来计算粒子权重，使粒子群经过重采样后更加集中在正确的位置，降低了机器人位姿的不确定性。文献[7]利用里程计信息和激光雷达的距离信息相融合，有效降低了粒子滤波阶段的粒子数量，但是系统鲁棒性较低。文献[8]通过引入动态误差，提高激光雷达数据的有效性，降低了噪声对测量数据的影响。文献[9]提出了一种快速联合兼容关联方法，提供准确的观测数据和特征匹配的关系。文献[12]提出利用激光雷达得出标志物与机器人的相对位置，计算出机器人的绝对位姿，将这些绝对位姿并入粒子采样中，采样分布更为集中。该方法只利用激光雷达传感器，接收数据单一，且激光雷达易受环境的干扰，影响定位准确性。文献[13]提出了利用里程计信息和惯性测量单元的信息进行融合，来修正里程计的累积误差，提高定位精度。此方法在机器人运动时受到本身漂移和重力的影响，定位效果不佳。文献[16-17]提出融合周围环境的点线特征。来进行环境匹配，完成机器人的定位，但视觉易受光线的影响，容易产生环境的误匹配，无法对错误的定位及时矫正。文献[24]利用激光传感器和视觉传感器联合感知环境信息，采用分阶段的形式来判断障碍物，可以较好地识别障碍物，但是存在计算量大、实时性差等问题。文献[25]采用提取激光与视觉信息的一致性特征信息进行信息融合来判断机器人的位姿情况，可是实验成功率不高。

在现有机器人定位方法中，一般都是采用里程计、激光雷达、视觉传感器等其中一种数据，数据来源较为单一，部分方法[7,13,24-25]采用其中两种以上传感器数据进行信息融合，一定程度上提高了定位的准确性。然而持续的数据融合增加了数据处理复杂度，增加了计算量，特别是包含视觉传感器时，增加了很大的计算量以及机器人的负担和能量消耗。针对以上问题，本文提出采用基于粒子滤波的AMCL优化定位算法，在粒子滤波过程的预测阶段，利用高精度的激光雷达数据和双目摄像机数据来改善其提议分布，其中双目摄像机和激光雷达数据的融合只在特定位置和时间段进行以减少计算量；其次，改进激光雷达的点云匹配过程，使得机器人能够更好地估计其位姿。机器人平台上的实验结果证明，本文方法在保证计算量的前提下，一定程度上提高了机器人的定位精度。

1 基于粒子滤波的定位算法优化

1.1 粒子滤波原理

AMCL定位算法是目前常用的预测机器人位姿的粒子滤波方法，能实现机器人较为精准的定位[3]。定位阶段分为预测阶段、测量阶段和重采样阶段[4]。预测阶段是根据里程计输入的速度信息和前一时刻机器人的位姿粒子分布来采样当前时刻的位姿粒子群；测量阶段是根据激光雷达的扫描数据作为输入，对每一个粒子进行权值计算；重采样阶段是根据粒子权值来对粒子进行筛选，舍弃权值低的粒子，保留权值高的粒子，即为接近机器人真实位姿的粒子。若没有达到足够的粒子数来表示真实位姿，则需要重复这三个过程，最终使绝大部分粒子聚集于真实位姿最接近的区域，实现定位。其后验概率分布为[9]：

P(xt|z1∶t,u1∶t)=

(1)

1.2 粒子滤波算法流程及其优化

1) 预测阶段。首先，规定粒子数量，将粒子平均分布于规划区域，然后输入轮式里程计数据，根据里程计的运动模型，得到一个提议分布。以下为轮式里程计输入模型。假设机器人在t-1时刻的位姿为Xt-1(xt-1,yt-1,θt-1),t时刻的位姿为Xt(xt,yt,θt)，里程计输入数据为左轮速度VL和右轮VR,两轮之间距离为2d，则机器人速度V和角速度ω(以顺时针方向为正)为[10-11]：

(2)

则机器人从t-1时刻到t时刻的位姿关系变化可以表示为：

(3)

2) 测量阶段。测量阶段需要以激光雷达数据作为输入，得到一个较为准确的机器人位姿。激光雷达输入模型如图1所示。

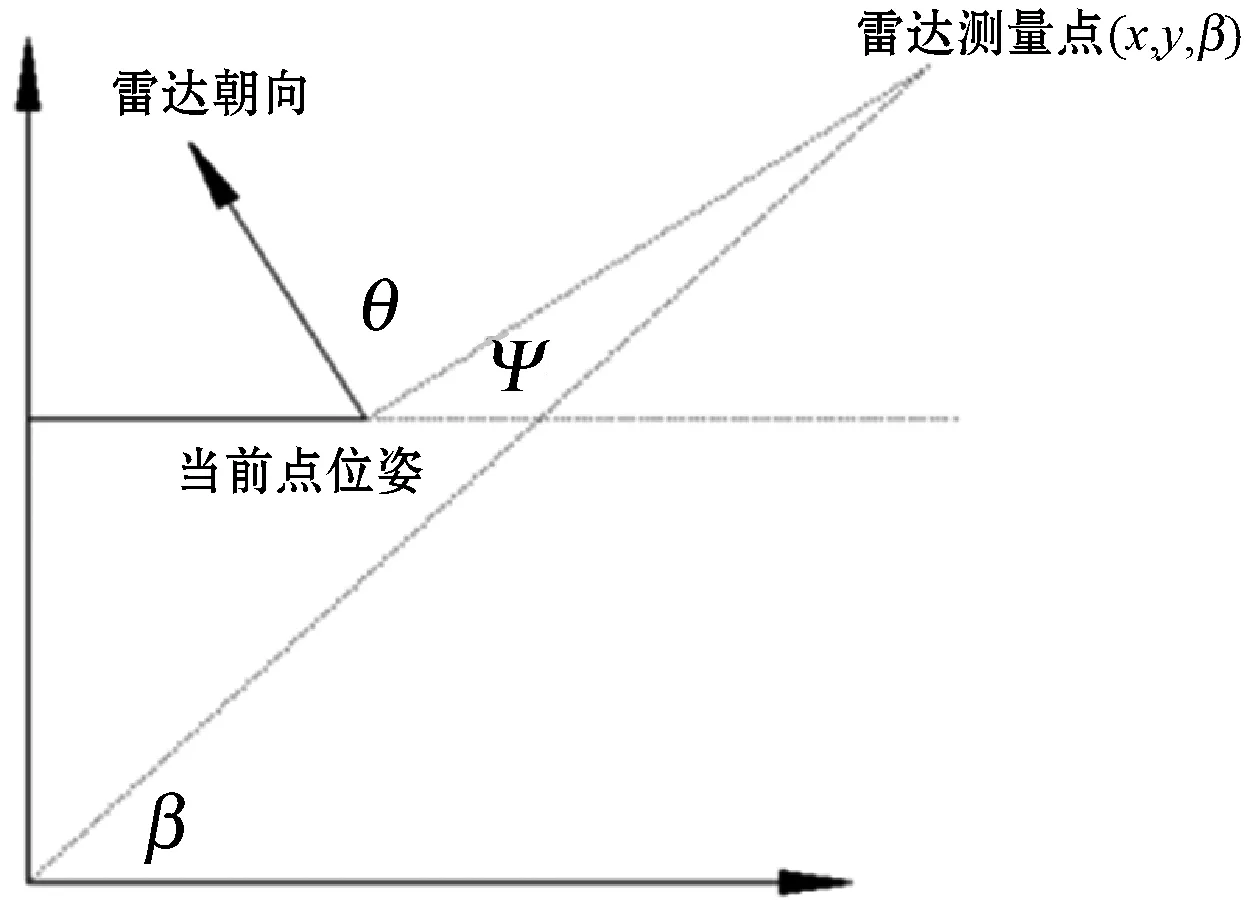
图1 激光雷达坐标系

经过一段位移后，机器人位于A点，雷达的朝向就是机器人的朝向。此时，机器人的位姿为Xt(xt,yt,ψt)，雷达测量角为θ，测量到障碍物距离为d,设雷达测量点为B(x,y,β),则根据几何关系可得[10-11]：

(4)

由此输入激光雷达数据，得到观测值z，对每个粒子进行评价，根据下式对每个粒子进行权重估计[15]：

(5)

由权值大小来判定粒子是否接近真实情况。

3) 重采样阶段。对于某一个粒子，以权重为wi的概率来接受这个粒子，并落在其接受的区间，保留权重大的粒子，舍弃权重小的粒子，为了保持粒子总数不变，复制权重大的粒子根据权重的比例重新分布粒子。将重采样后的粒子代入到状态转移函数中，就能获得新的预测粒子，经过反复迭代，使得大部分粒子接近真实情况，获得机器人准确位姿，实现机器人的定位。

4) 粒子滤波优化流程。理论上，提议分布越接近目标分布，滤波效果越好。然而，典型的粒子滤波应用是采用里程计运动模型来得到提议分布的。这种运动模型的优点在于方便计算；缺点是样本过于分散，方差较大。根据激光雷达数据采样的粒子，方差较小，粒子分布更为集中，如下式所示：

(6)

本文提出在特定位置(路口、转弯处和障碍物附近)和时间段采用双目视觉和激光雷达融合的观测数据和里程计数据相联合来优化提议分布。

双目摄像机每帧数据庞大，本文采用ORB特征检测方法，对特征点进行提取[14]。

如图2所示，在实际过程中，当双目摄像机识别出关键位置的图像时，将激光雷达数据和双目摄像机数据进行匹配，对应环境中的同一特征点。

图2 双目摄像机深度图像

设双目摄像机扫描到物体点特征的角度为以下形式：

ΘV=[θv,1θv,2…θv,n]

(7)

激光雷达扫描到物体点云的角度为以下形式：

ΘL=[θl,1θl,2…θl,n]

(8)

相机坐标系下的扫描点的角度信息，经过旋转变换之后，转换到激光雷达下的坐标系,将角度信息进行融合。

已知单位向量的旋转变换如下所示[19]：

bi=Ari+Δbii=1,2，…,n

(9)

(10)

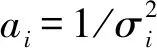
将扫描点的角度信息从摄像机坐标系转换到激光雷达坐标系，用下式表示：

(θl,i)real=R(θv,i)real

(11)

式中：(θl,i)real为激光雷达扫描角度信息在激光坐标系上的真值，(θv,i)real为摄像机扫描角度信息在相机坐标系上的真值。激光雷达和双目摄像机在收集数据时存在测量误差，为Δθl,i和Δθv,i，若误差符合正态分布，则两者转换关系为：

θl,i-Δθl,i=R(θv,i-Δθv,i)

(12)

θl,i=Rθv,i-RΔθv,i+Δθl,i

(13)

则求解旋转矩阵R如下式所示：

(14)

(15)

R=UVT

(16)

在机器人运行过程中，将最近一次的双目摄像机和激光雷达联合观测得到的样本，集成到提议分布中，以此将提议分布集中在可能性更高的区域。

根据式(13)，得到改进后的提议分布函数为：

(17)

根据此提议分布，利用式(14)计算得到权重，进行重采样。根据优化后的提议分布，可以忽略分布中意义不大的区域，使粒子分布更为集中，减少重采样部分的计算量。

(18)

在重采样阶段，根据激光雷达和双目摄像机的融合观测数据，计算得到粒子的权重来进行重采样，为下一次的预测阶段提供输入，经过反复迭代之后，得到机器人正确的位姿。具体流程为：

5) 将新的高斯分布作为提议分布，从该分布中得到新的位姿。算法过程如下：

参数St-1：上一时刻的采样集

zt：最新的融合观测

zVt：最新的视觉扫描

zLt：最新的激光扫描

ut-1：最新的里程计测量

St：最新的采样集。

St={}

//视觉扫描匹配

//激光扫描匹配

else

//从极值附近采样

fork=1,2,…,Kdo

end for

//计算高斯分布

η(i)=0

for allxj⊂{x1,x2,…,xK} do

end for

end for

end for

//采样新的位姿

end if

1.3 扫描匹配优化流程

1) ICP匹配原理。激光雷达扫描过程中，主要是根据ICP匹配算法。当前后两帧激光数据为同一个点的点云时，记为数据集P和Q，需要在点云Q中找出qi，与点云P中的pi相对应，如下式所示[22]：

(19)

根据qi和pi求得旋转变换矩阵R和平移矩阵T。如图3所示，由于机器人只在平整地面上移动，所以只考虑关于Z轴的旋转。P点由XaYa坐标轴，旋转到XbYb坐标轴，为qi所在的坐标轴，则可计算出旋转矩阵R。

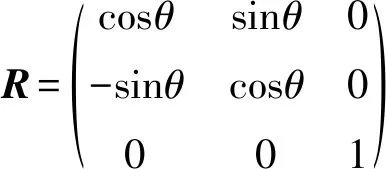
(20)

该匹配需对一批点云的每一个点进行最近邻点匹配，计算量大，结果可能会陷入局部最优问题。

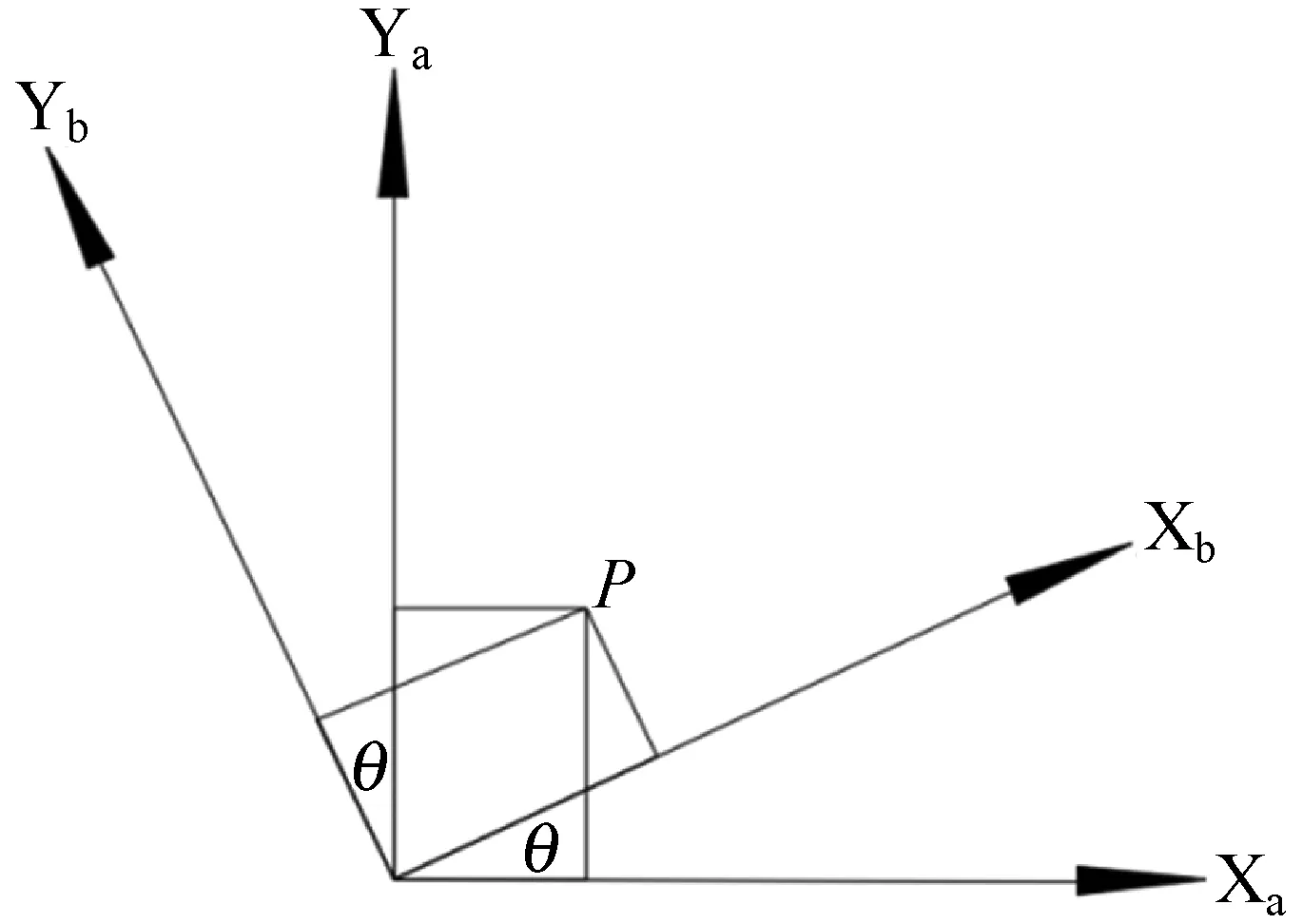
图3 旋转矩阵变换

2) 点云匹配优化流程。本文提出一种分组阶梯式阈值匹配法。在机器人局部路径规划中，在时间Δt内，激光雷达扫描到新的障碍物，在Δt内障碍物为静止。以激光雷达对障碍物扫描的前后两帧的数据作为两个集合，为M集合和N集合。根据扫描的时间先后顺序将M和N从头至尾平均分为k组，在M和N之间对应的每一组的点云来进行最近邻点匹配，根据ICP算法，对每组的每一个点云进行匹配。在一定时间内，若匹配率达到阈值，则表明这两组点云匹配成功；若匹配成功组数达到阈值，则表明这批点云匹配成功，以此来成功识别出该障碍物，重新进行局部路径规划。算法主要流程如下：

(1) 将激光雷达的前后两帧扫描作为点云数据，分别作为M点集和N点集。

(2) 将M点集和N点集分别分成k组，记为M1，M2，M3，…，Mk和N1,N2,N3，…，Nk，设每组平均个数为C。

(3) 将Mij和Nij点云进行ICP匹配，(Mij表示M点集中第i组的第j个点云)利用下式计算两个点云Mij和Nij的质心。

(21)

(4) 利用SVD分解来求得变换矩阵,以下式来求得U、V。

(22)

若rank(W)=3,则求得解唯一，利用下式求得旋转变换矩阵R和平移矩阵T′：

R=U′V′TT′=μm-Rμn

(23)

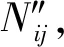
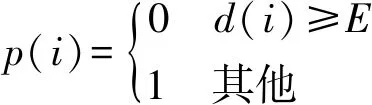
(24)

式中：p(i)用来判断点匹配是否合格，E为经过试验得到的距离阈值。

(6) 若Mi、Ni的匹配率达到阈值ζ(匹配率为该组成功点云数除以该组点云总数)，停止迭代，则表明这两组对应点云匹配成功。若M、N的匹配组数达到阈值β，停止迭代，则表明M、N点集匹配成功。

2 实验与数据分析

实验采用的机器人为Autolabor Pro1,如图5所示，是一款集机器人底盘、控制计算机、传感器为一体的室内导航移动平台。平台搭载激光雷达、惯导、里程计等传感器，可实现Navigation定位导航功能。

图4 ROS机器人平台

实验中采用的AMCL工具包为ROS平台Navigation包的一部分。利用Ubuntu16.04操作系统进行操作，在rviz中进行可视化。已知地图是利用ROS平台的GMapping工具包进行创建的，图5所示为本校电子信息楼4楼二维地图。

图5 室内全局图

实验中，机器人利用HF、AMCL和本文算法进行定位操作，场地分别选定为实验室室内与外部走廊，如图6、图7所示。图6中的(a)、(b)、(c)分别为机器人利用HF、AMCL和本文算法在实验室室内的定位结果；图7中的(a)、(b)、(c)为机器人利用这三种方法在外部走廊的定位结果。由实验可以得出，利用HF算法和AMCL算法，在机器人运动一段时间后机器人定位均出现了不同程度的偏差，本文算法机器人定位性能较稳定，且定位精度较高。

(a) HF (b) AMCL (c) Proposed图6 实验室室内定位结果

(a) HF (b) AMCL (c) Proposed图7 外部走廊定位结果

图8给出了不同方法下机器人定位误差的结果比较，其中：(a)为机器人的距离均方根误差，(b)为航向角角度误差。可以看出，本文算法在距离和角度误差中均为最小，曲线较为平缓。HF算法精度较高，均方根误差和角度误差与本文方法误差接近，但是存在波动较大的情况。AMCL算法稳定性较高，但定位误差较大。

(a) 角度误差曲线

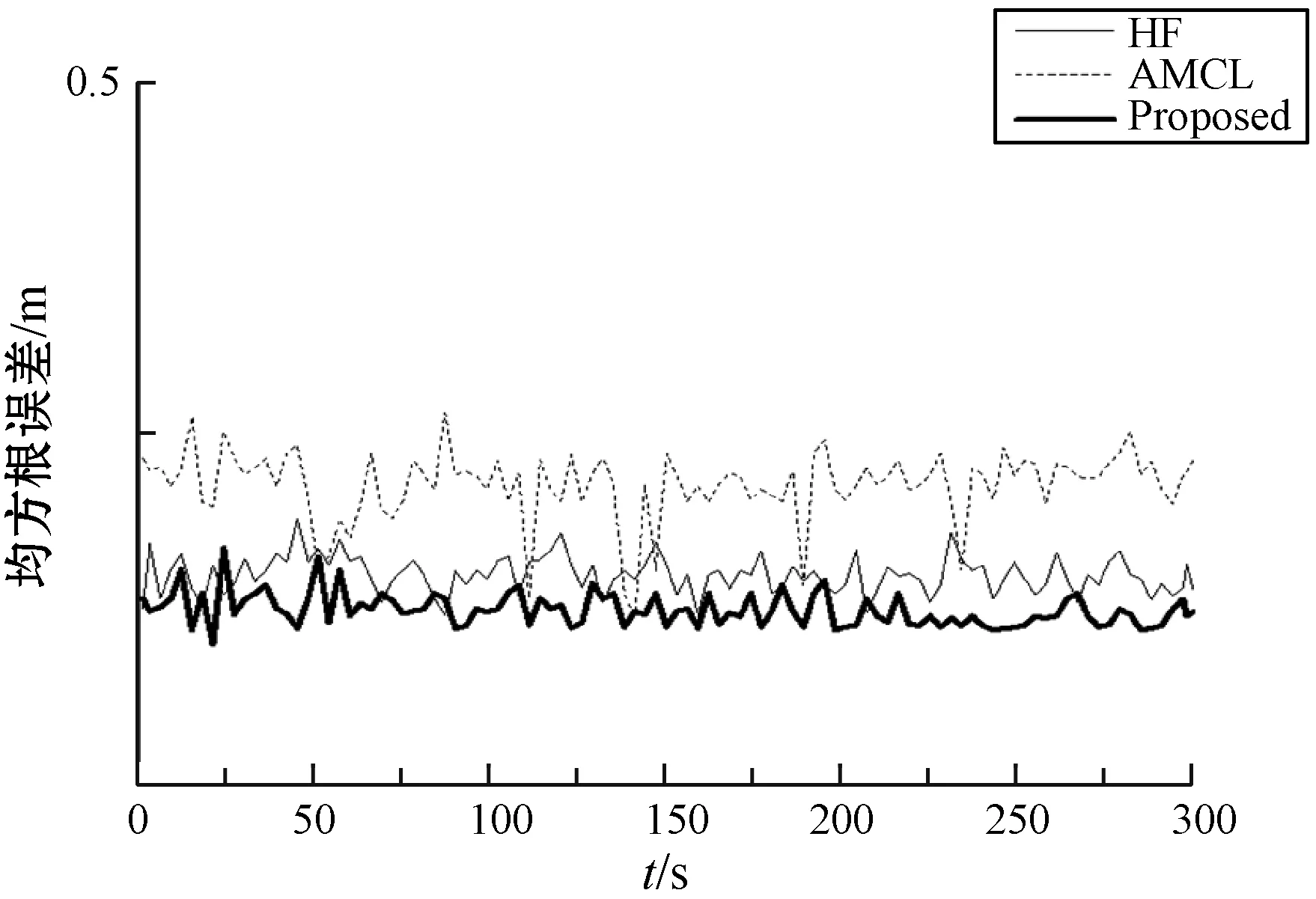
(b) 位姿估计误差曲图8 误差比较图

表1显示了三种方法在不同初始位姿偏差的情况下的定位结果，包括横向(Lateral)、纵向(Longitudinal)和航向角(Yaw)。图9为横向误差、纵向误差、航向角角度误差和时间消耗与初始位姿偏差的关系曲线，显示了随着初始位姿偏差的增大，各参数值的变化情况。由表1和图9可以得出，在不同初始位姿偏差的情况下，不论是横向，纵向还是角度偏差，本文算法误差最小，完成定位时间最短。HF算法在初始位姿较小的情况下，定位精度较高，但是在初始位姿偏差较大的情况下，定位效果差，误差较大。AMCL传统算法稳定性较好，但定位精度不高。

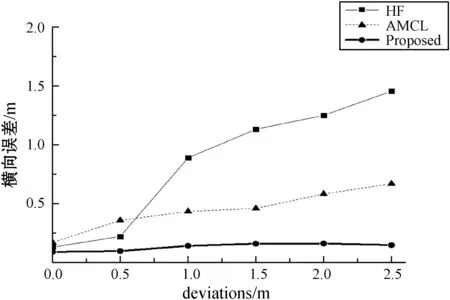
(a) 横向定位误差曲线

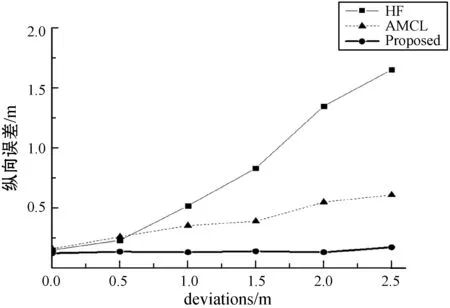
(b) 纵向定位误差曲线

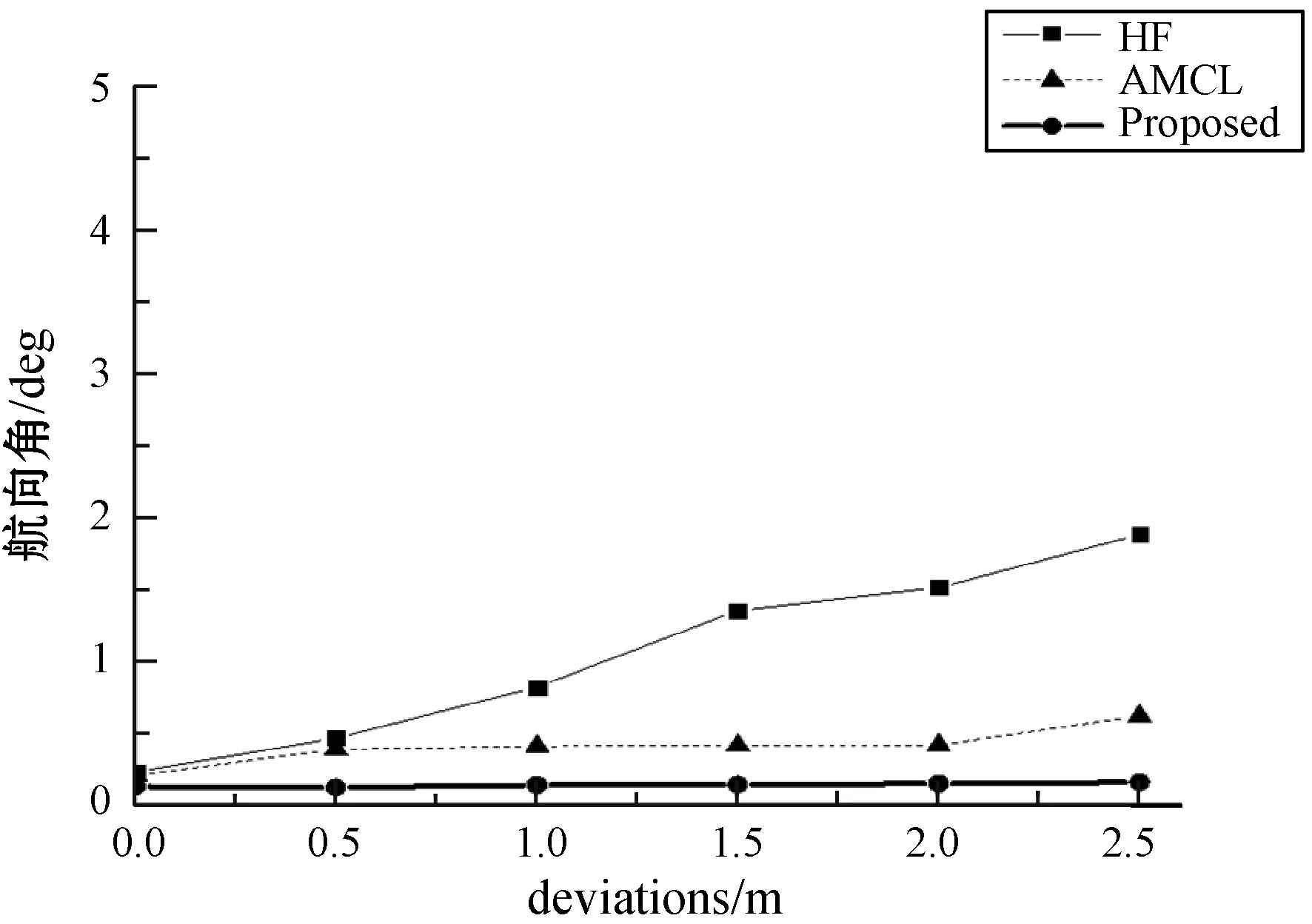
(c) 角度误差曲线

(d) 定位时间消耗曲线图9 不同初始位姿偏差下定位结果曲线

表1 不同初始位姿偏差下定位结果对比

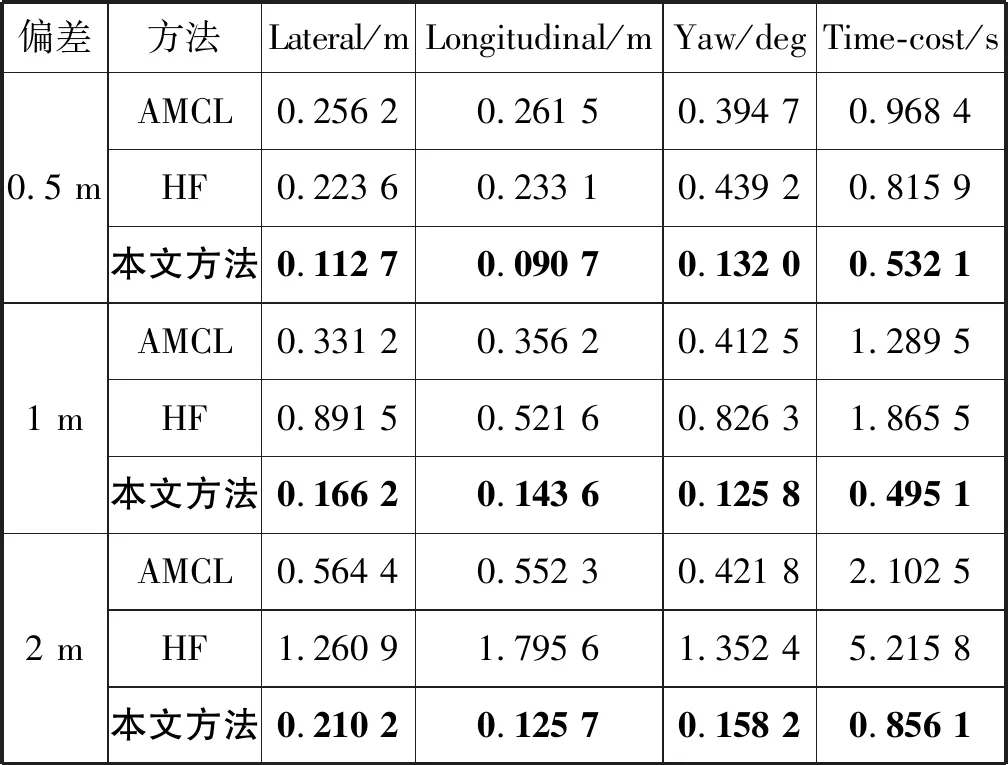
偏差方法Lateral/mLongitudinal/mYaw/degTime-cost/s0.5 mAMCL0.256 20.261 50.394 70.968 4HF0.223 60.233 10.439 20.815 9本文方法0.112 70.090 70.132 00.532 11 mAMCL0.331 20.356 20.412 51.289 5HF0.891 50.521 60.826 31.865 5本文方法0.166 20.143 60.125 80.495 12 mAMCL0.564 40.552 30.421 82.102 5HF1.260 91.795 61.352 45.215 8本文方法0.210 20.125 70.158 20.856 1

3 结 语

本文主要研究了智能机器人的定位问题，并针对现有采用里程计、激光雷达、视觉摄像机等数据在定位过程中存在精度有限且计算量较大的问题，提出了基于粒子滤波的AMCL优化定位方法。该方法利用双目摄像机数据和激光雷达数据改进基于轮式里程计的提议分布，使提议分布更为集中，并且减少重采样过程的粒子数目，其中双目摄像机与激光雷达数据的融合只在特定位置和时间段进行以减少计算量；利用分组阶梯式阈值判断法进行障碍物的匹配，在保证匹配准确性的情况下，降低匹配计算量。实验结果表明，改进后的算法具有较高的定位精度，且能够较好地在实验平台中应用，具有良好的实用性。