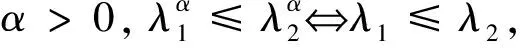两个独立部件并联系统的随机序性质
徐雅琳,陈 豪,蔡南莲
(集美大学理学院,福建 厦门 361021)
0 引言
指数分布的无记忆性和良好的数学结构,使得它在产品的可靠性分析、运筹学等领域中被广泛使用,如文献[1]对指数分布的性质和应用进行了较系统的研究。同时,由于成比例故障率(proportional hazard rate,PHR)模型可化为指数分布模型来研究,韦布尔分布模型是PHR模型的特殊情形,从而PHR模型和韦布尔分布模型的应用及研究也受到学者们越来越多的关注,如文献[2-3]在部件寿命服从PHR模型或韦布尔分布模型的前提下,讨论了并联系统的随机比较性质。
次序统计量是统计推断、拍卖理论、可靠性理论等领域很重要的概念,有着广泛的应用。在可靠性理论中,k/n系统是指n个部件组成的系统,当且仅当n个部件中至少有k个部件正常工作,系统才能正常工作。特别地,1/n系统、n/n系统分别对应着并联系统和串联系统。设第i个部件的寿命为随机变量Xi(i=1,…,n)。X1,…,Xn的次序统计量为X1:n≤…≤Xn:n,则并联系统、串联系统的寿命分别为Xn:n和X1:n,k/n系统的寿命为Xn-k+1:n。近年来,极值次序统计量的随机比较性质的研究已成为学界研究的热点之一,如:Boland 等[4]研究了两个独立的不同指数分布的部件组成的并联系统的故障率性质,并得到故障率的上界;Khaledi等[5]进一步研究了多个指数部件并联系统的情形,得到了n个非齐次指数分布并联系统的故障率的上界,该结论优于文献[4]得到的;Zhao等[6]讨论了具有不同参数指数分布的两个部件的并联系统的故障率序、反故障率序、似然比序意义下的随机比较性质。随后,Balakrishnan等[7]对近年来在部件寿命服从独立指数分布情形下有关次序统计量的随机比较性质的研究进行了较全面的综述。
1 定义
下面介绍随机序、PHR模型及向量超优序的定义,更多的性质可参阅文献[8-9]。文中均假设随机变量非负,分布函数是绝对连续的,具有概率密度函数;“单调增加”均指“单调不降”,“单调减少”均指“单调不增”。
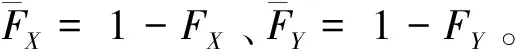
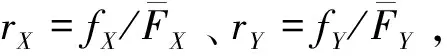
上述随机序有如下关系:X≤lrY⟹X≤hrY⟹X≤stY;X≤lrY⟹X≤rhY⟹X≤stY(见文献[8])。

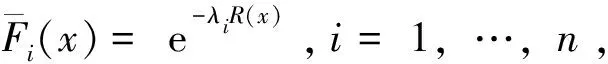
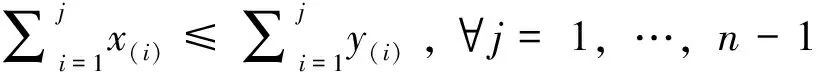
2 引理
在证明主要结果之前,先介绍一些引理。
引理1 对于任意x∈R+, 函数(1-e-x)/x和xe-x/(1-e-x)关于x单调减少。
证明见文献[6]引理3.1。

证明见文献[8]定理1。
引理3 设X、Y是两个随机变量,g(x)是单调增加函数,则有:1)设X≤stY,则g(X)≤stg(Y);2)设X≤hrY,则g(X)≤hrg(Y);3)设X≤rhY,则g(X)≤rhg(Y);4)设X≤lrY,则g(X)≤lrg(Y)。
证明见文献[8]定理1。
引理4 设λ1≤λ≤λ2,λ1、λ2、λ均为大于零的常数,φ(t)=[λ1e-λ1t/(1-e-λ1t)+λe-λt/(1-e-λt)]/[λ2e-λ2t/(1-e-λ2t)+λe-λt/(1-e-λt)],t>0,则φ(t)关于t单调增加。
证明两边求导得:φ′(t)[λ2e-λ2t/(1-e-λ2t)+λe-λt/(1-e-λt)]2=[-λ12e-λ1t/((1-e-λ1t)2)-λ2e-λt/((1-e-λt)2)]×[λ2e-λ2t/(1-e-λ2t)+λe-λt/(1-e-λt)]-[-λ22e-λ2t/((1-e-λ2t)2)-λ2e-λt/((1-e-λt)2)]×[λ1e-λ1t/(1-e-λ1t)+λe-λt/(1-e-λt)]。将等式展开得:φ′(t)[λ2e-λ2t/(1-e-λ2t)+λe-λt/(1-e-λt)]2=[-λ12λ2e-(λ1+λ2)t/((1-e-λ1t)2(1-e-λ2t))-λλ12e-(λ+λ1)t/((1-e-λ1t)2(1-e-λt))-λ2λ2e-(λ+λ2)t/((1-e-λt)2(1-e-λ2t))-λ3e-2λt/((1-e-λt)3)]-[-λ22λ1e-(λ1+λ2)t/((1-e-λ2t)2(1-e-λ1t))-λλ22e-(λ+λ2)t/((1-e-λ2t)2(1-e-λt))-λ1λ2e-(λ+λ1)t/((1-e-λt)2(1-e-λ1t))-λ3e-2λt/((1-e-λt)3)]。整理得:
φ′(t)[λ2e-λ2t/(1-e-λ2t)+λe-λt/(1-e-λt)]2=λ1λ2e-(λ1+λ2)t/((1-e-λ1t)(1-e-λ2t))[λ2/(1-
e-λ2t)-λ1/(1-e-λ1t)]+λλ2e-(λ+λ2)t/((1-e-λt)(1-e-λ2t))[λ2/(1-e-λ2t)-λ/(1-e-λt)]+
λλ1e-(λ+λ1)t/((1-e-λt)(1-e-λ1t))[λ/(1-e-λt)-λ1/(1-e-λ1t)]=A+B,
(1)
其中:A=λ1λ2e-(λ1+λ2)t/((1-e-λ1t)(1-e-λ2t))[λ2/(1-e-λ2t)-λ1/(1-e-λ1t)],B=λλ2e-(λ+λ2)t/((1-e-λt)(1-e-λ2t))[λ2/(1-e-λ2t)-λ/(1-e-λt)]+λλ1e-(λ+λ1)t/((1-e-λt)(1-e-λ1t))[λ/(1-e-λt)-λ1/(1-e-λ1t)]。

命题1[6]设X1与X2相互独立,分别服从参数为λ1和λ的指数分布,Y1与Y2相互独立,分别服从参数为λ2和λ的指数分布。令X2:2=max(X1,X2),Y2:2=max(Y1,Y2)。设λ≥max(λ1,λ2),则X2:2≥lrY2:2⟺λ1≤λ2。
命题2[6]设X1与X2相互独立,分别服从参数为λ1和λ2的指数分布,Y1与Y2相互独立,分别服从参数为λ1*和λ2*的指数分布。令X2:2=max(X1,X2),Y2:2=max(Y1,Y2)。设min(λ1,λ2)≤min(λ1*,λ2*)≤max(λ1*,λ2*)≤max(λ1,λ2),则:
本文假设X1与X2相互独立,Y1与Y2相互独立。令X2:2=max(X1,X2),Y2:2=max(Y1,Y2),根据λ、λ1与λ2的大小关系,讨论X2:2与Y2:2在随机序、似然比序、故障率序、反故障率序下的随机比较性质,得到定理1是上述已有命题1的补充,定理2及定理3是命题2的补充。
3 主要结果
3.1 指数分布情形
本节考虑服从指数分布的两个部件组成的并联系统,当其中一个部件的参数固定,另一个部件的参数变化时,并联系统寿命的随机序性质。

定理1 设X1、X2相互独立,分别服从参数为λ1和λ的指数分布,Y1、Y2相互独立,分别服从参数为λ2和λ的指数分布,λ1,λ2,λ>0且λ≥min(λ1,λ2),则X2:2≥lrY2:2的充要条件是λ1≤λ2。

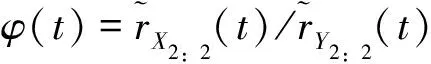
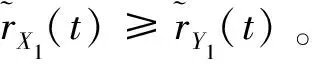
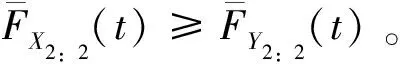
(2)
其中ο(t2)表示t2的高阶无穷小。
同理,
(3)
由式(2)和式(3)得:1-λλ1t2+ο(t2)≥1-λλ2t2+ο(t2),两边同除以t2得:-λλ1+o(t2)/t2≥-λλ2+o(t2)/t2,令t→0,得λλ1≤λλ2,即λ1≤λ2。
下面的命题3说明,定理1中如果条件λ≥min(λ1,λ2)不满足,即λ 命题3 设X1、X2相互独立,分别服从参数为λ1和λ的指数分布,Y1、Y2相互独立,分别服从参数为λ2和λ的指数分布,λ1,λ2,λ>0。若λ 定理2 设X1、X2相互独立,分别服从参数为λ1和λ的指数分布,Y1、Y2相互独立,分别服从参数为λ2和λ的指数分布,λ1,λ2,λ>0。设λ≥min(λ1,λ2),则下列条件等价:1)λ1≤λ2;2)X2:2≥lrY2:2;3)X2:2≥hrY2:2;4)X2:2≥rhY2:2;5)X2:2≥stY2:2。 证明由于X≤lrY⟹X≤hrY⟹X≤stY,X≤lrY⟹X≤rhY⟹X≤stY,且由定理1得1)⟺2),故只需证5)⟹1),1)⟹4)。 5)⟹1):设X2:2≥stY2:2,要证λ1≤λ2。 与定理1必要性部分证法相同。 注1 定理2中,当min(λ1,λ2)≤λ≤max(λ1,λ2)时,并不满足文献[6]定理3.4、定理4.3的条件,故定理2的结论是文献[6]定理3.4、定理4.3的补充。 定理3 设X1、X2相互独立,分别服从参数为λ1和λ的指数分布,Y1、Y2相互独立,分别服从参数为λ2和λ的指数分布。对于任意的λ>0,则下列条件等价:1)λ1≤λ2;2)X2:2≥rhY2:2;3)X2:2≥stY2:2。 证明因X≤rhY⟹X≤stY,只需证1)⟹2),3)⟹1)。 3)⟹1):设X2:2≥stY2:2,要证λ1≤λ2。证法与定理1必要性部分证法相同。 注2 定理3中,当λ≤min(λ1,λ2)时,并不满足文献[6]定理3.4的条件,故定理3的结论是文献[6]定理3.4的补充。 下面考虑部件分布服从PHR模型时,并联系统寿命的随机序性质。 令U2:2=max(U1,U2),因R(x)是单调增加函数,故 U2:2=max(R(X1),R(X2))=R(max(X1,X2))=R(X2:2)。 (4) 再次利用R(x)及R-1(x)是单调增加函数,通过引理3,将PHR模型转化为已有指数分布的情形,得到定理4和定理5。 证明沿用上述的记号,令Ui=R(Xi),Vi=R(Yi)。U1,U2分别服从参数为λ1和λ的指数分布,V1,V2分别服从参数为λ2和λ的指数分布。由式(4)得U2:2=R(X2:2),V2:2=R(Y2:2)。 1)⟹2):已知λ1≤λ2,要证X2:2≥lrY2:2。由定理2有:U2:2≥lrU2:2。因R-1(x)是单调增加函数,由引理3得R-1(U2:2)≥lrR-1(V2:2),即X2:2≥lrY2:2。 2)⟹1):已知X2:2≥lrY2:2,要证λ1≤λ2。因R(x)是单调增加函数,由引理3得U2:2=R(X2:2)≥lrR(Y2:2)=V2:2,再由定理2得λ1≤λ2, 故1)⟺2)。 同理可类似证明1)⟺3)⟺4)⟺5)。 注3 定理4中,当min(λ1,λ2)≤λ≤max(λ1,λ2)时,并不满足文献[7]定理2.8的条件,且定理4给出的是使X2:2≥lrY2:2成立的充要条件,而已有文献[7]定理2.8给出的是使X2:2≥lrY2:2成立的充分条件,故定理4是文献[7]定理2.8的补充。 下面是部件服从韦布尔分布时的相应结论。 推论1 设X1、X2相互独立,服从相同的形状参数α,尺度参数为λ1和λ的韦布尔分布,Y1、Y2相互独立,服从相同的形状参数α,尺度参数为λ2和λ的韦布尔分布,λ1,λ2,λ,α>0,假设λ≥min(λ1,λ2),则下列条件等价:1)λ1≤λ2;2)X2:2≥lrY2:2;3)X2:2≥hrY2:2;4)X2:2≥rhY2:2;5)X2:2≥stY2:2。
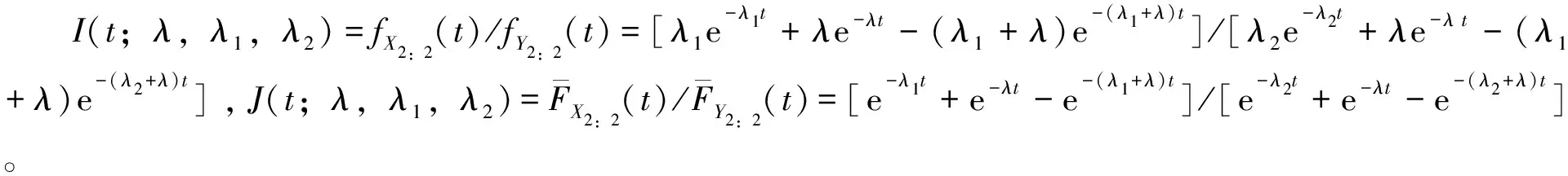


3.2 PHR模型情形