核心素养导向下初中生数学推理能力的培养

福建省漳州市台商投资区角美中学 曾丽琴

目前，初中数学教学尚存在着一些不足，教师在实际教学中不重视应用推理，对推理能力缺少清晰认识，同时课程教学资源以教材为主。教法上，不重视突出“以学生为中心”的教学理念，对于教学情境的创设也不恰当，令学生难以掌握类比推理、统计推理等推理方法，阻碍了学生数学核心素养的发展。在这样的背景下，学校和教师要积极优化对学生推理能力的培养。

一、整合知识内容，鼓励推理

实际教学中，教师面对相对零散的知识点，可应用归纳推理方法对教材内容进行整合，以促进学生更好地理解教材内容，有针对性地向学生渗透推理意识。在教材内容具体整合过程中，要运用好先进技术设备，全面搜集教学内容，以拓宽学生的知识视野。同时，教师在对知识进行整合时，为鼓励学生展开归纳推理行为，要鼓励学生自主建立知识点之间的联系，对知识脉络进行梳理。在这个过程中，学生不仅能掌握课堂知识，还将从知识建构中获得丰富的归纳推理经验。例如，在“一元一次方程”章节内容教学时，教师可先为学生耐心讲解一元一次方程的解法、步骤等知识点，引导学生体验其基本思想。待知识点讲授完毕以后，教师可要求学生自主绘制思维导图，对整个章节内容进行整理，学生自主归纳推理出“一元一次方程”知识脉络。归纳推理中，有的学生将尝试以“一元一次方程”为中心建立思维导图，再由中心合情推理出定义、方程的解、解方程、等式的性质、解一元一次方程的步骤、列一元一次方程解应用题等分支。然后由解一元一次方程的步骤合情推理出去分母、去括号、移项、合并同类项、系数化为1 的具体步骤内容。知识整合中，学生的推理意识会自然而然有所提高，课堂教学效率也将有所提升。

二、进行深度思考，激发推理

以往初中数学课堂教学主要以“灌输式”教学为主，存在着表面化问题，影响学生核心素养发展。基于此，教师在对学生推理能力核心素养进行培养时，要引导学生进行深度思考，以激发学生积极展开推理活动。课堂上，为了能让学生进行深度思考，教师要把握好提问技巧，根据教学重点有目的地向学生提问，鼓励学生自主推理问题的正确答案。同时，提问时要注意因材施教，要重视设计与学生实际生活相关的问题。如此才能使学生全身心地投入深度思考中，掌握相关推理技巧。例如，在“函数”一课教学中，为深化学生对函数的感知，可结合学生实际生活体验，提出问题：“你坐过摩天轮吗？当你坐在摩天轮上时，随着时间的变化，你离开地面的高度是如何变化的？”在问题导向下，向学生展示旋转时间t（分）与摩天轮上一点高度h（米）之间的关系图，再给定时间t，请学生深度思考，推理出当时间t 是0 分钟、1 分钟、2 分钟、3 分钟……时所对应的高度h，用列表法展示时间t（分）和高度h（米）之间的关系。在这个过程中，学生将通过深度思考，推理出列表法函数表示方法。接着，教师可继续创设问题情境，结合某市某天气温随时间变化的曲线图，向学生提出问题：“从曲线图中能获得哪些信息？”请学生用列表法表示各个时间对应的气温值，再顺势引出函数表示法的具体概念。然后，逐一说明函数概念理解中应注意的问题。

三、重视双向交流，夯实推理

古人云：“独脚难行，孤掌难鸣。”日常教学中，为夯实学生推理基础，教师要重视组织交流活动。交流中，学生将形成思维上的碰撞，于相互交流中共同探索推理出相关规律。为收到较好的推理能力培养效果，教师要扮演好“引导者”角色，向学生提出需要共同思考的问题，以便于学生展开相对积极的交流活动，共同突破推理障碍。这种方法能解决课堂教学时间有限的问题，给学生创造更多举例证明自己的机会。如在“探索三角形相似的条件”一课教学中，教师可向学生提出问题：“至少有几个角对应相等就能保证这两个三角形相似？”面对这个问题，不同的学生将提出不同的猜想。这时，教师可将全班学生分为若干个学习小组，让相同想法的学生为一组，组织学生相互交流证明猜想。期间，提出“至少一个角相等”想法的学生，在证明自己的猜想时，尝试用简捷方法画一个∠BAC 是60°的△ABC，再由另一人画∠B´A´C´是60°的△A´B´C´。交流中，学生将探索推理出有一个角对应相等的两个三角形不一定相似。提出“至少两个角相等”想法的学生，也尝试用相似的方法证明自己的猜想，在这个过程中，学生通过交流合情推理出自己的猜想是正确的，归纳出有两个角对应相等的两个三角形相似。整个教学活动过程中，教师通过创造良好的交流学习空间，夯实了学生推理能力核心素养，有利于让学生学会理性证明自己的猜想。

四、利用实践活动，创造推理

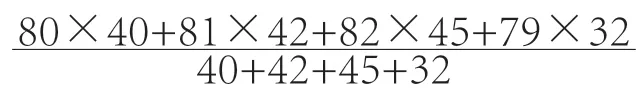
五、精心设计练习，考核推理

推理能力是学生所应具备的重要数学核心素养。在对学生数学推理核心素养进行培养时，教师除了要为学生创造推理机会，还要注意考核学生的推理能力，借助练习科学评价学生的推理水平，对学生的发展情况进行全面了解，有针对性地开展后续教学活动。在对学生推理能力进行考核时，为收到较好的考核效果，教师要精心设计卷面考试、脑筋急转弯、趣味提问等练习内容，利用不同形式完成考核。同时，在推理能力考核期间，教师要注意为学生营造良好的独立思考环境，给学生足够的思考时间，以便学生有序进行推理。其中，在“锐角三角函数”一课教学中，教师可先为学生耐心讲解锐角三角函数定义、性质，引导学生了解特殊角的三角函数值。当学生掌握了本节课所学知识以后，精心为学生设计练习题：“河坝横断面的迎水坡AB 的坡比是3 ∶4，坡高BC 是6m，求坡面AB 的长是多少？”面对这样一道练习题，学生运用自身已掌握的锐角三角函数知识进行推理，根据坡比求出，再结合BC=6m 这个已知条件求出AC 的值，得到，后通过建立勾股定理数学模型得到AB 是10m。求解练习题目过程中，学生将通过思考推理出将坡比化为三角函数值是解题关键，由此探索出问题的正确答案。在这里，教师通过设计练习，实现了对学生推理能力的考核，促进了学生推理能力的发展。

综上所述，学生要想学好数学，必须具备一定的推理能力。教师在对学生推理能力核心素养进行培养时，要鼓励学生自主整合教材内容，用适合的问题激发学生展开深度思考。同时，教师要重视组织交流活动和实践活动，并运用练习考核学生推理能力的发展情况。教师要在精准把握课程内容基础上，高效培养学生推理能力，提高课堂教学质量。