Application of the Static Headland-Bay Beach Concept to a Sandy Beach: A New Elliptical Model

LI Bing, ZHUANG Zhenye, CAO Lihua, 3), *, and DU Fengchao

Application of the Static Headland-Bay Beach Concept to a Sandy Beach: A New Elliptical Model

LI Bing1), 2), 3), ZHUANG Zhenye1), CAO Lihua1), 3), *, and DU Fengchao4)

1),,266100,2),,350400,3),,266100,4),,264006,

The headland-bay beach is one of the most common coastal types in the world. Its morphology reflects the changes that occurred during long-term evolution of the sandy coast. Several headland-bay beach models have been proposed to simulate the coastline’s configuration in equilibrium. In this paper, a new elliptical model is proposed, described, and applied. On the east coast of Laizhou Bay in Shandong Province from Longkou Port to Diaolongzui, four typical headland-bay beaches have developed, and four headland-bay beach models are used in this paper to simulate the morphology of these beaches to assess the applicability of each model. The simulation results of the elliptical model verify that it is applicable to the study area. In addition, the elliptical model is easy to use. Through simulation and field investigations, we concluded that most of the coastal segments in this area will remain in an erosion state, and the human activity has a significant impact on the shoreline’s evolution.

static headland-bay beach concept; elliptical model; sandy beach; coastal erosion; east coast of Laizhou Bay

1 Introduction

Due to the needs of coastal protection and offshore engineering, researchers and engineers began studying the plane morphology of headland bays early last century (Halligan, 1906), but most progress was made after World War II when scholars attempted to describe the morphology of headland bays with mathematical expressions (Kru- mbein, 1944). They gradually related the plane form of a headland bay with its stability, and they tried to determine the plane morphology of a headland bay in equilibrium through numerical simulations, model testing, and other methods. Headland bays in equilibrium can be divided into two types. One is a headland bay in static equilibrium, in which there is no sediment transport and no sediment exchange with areas outside of the bay. The second is a headland bay in dynamic equilibrium. Its form is influenced by sediment transport, and when the sediment transport conditions change, the form of the bay also changes until it reaches a new equilibrium (Hsu., 2000).

Krumbein (1944) was the first to propose a logarithmic spiral equation for the study of Half Moon Bay in California, USA. Yasso (1965) applied this equation to natural headland bays on the east and west coasts of the United States and found that the center of the logarithmic spiral did not coincide with the wave diffraction point of the bay. Silvester (1970) studied the relationship between the parameters and wave diffraction factors of the equation. Since then, inspired by this point of view, other equilibriumheadland-bay models have been proposed. Using data from 13 experimental models and 14 stable beaches, Hsu and Evans (1989) summarized the plane form of a headland bay in equilibrium as a second-order polynomial, parabolic model that has since been accepted and widely used. Tan and Chiew (1994) further simplified the parabolic model and integrated three coefficients to describe the form of a headland bay in equilibrium. Xia (1988) proposed a hyperbolic model for a headland bay in static equilibrium based on experiments, and he discussed its practical applications in offshore engineering. Moreno (1997) proposed a hyperbolic tangent model for the engineering design of static headland-bay beaches. Then, Moreno and Kraus (1999) simplified this model to make it easy to use.

The static headland-bay beach concept provides a good approach to issues such as beach stability assessment, erosion prediction, and coastal protection. Many scholars have compared the advantages and disadvantages of the various models, their applicability to various coasts, the influence of waves, their practical applications, and other factors that influence the models (Chen, 1999; Dai, 2004; Li and Chen, 2006, 2007; Yang and Zhang, 2007; Yu and Chen, 2010; Li., 2014).

On the east coast of Laizhou Bay, Shandong Province (Fig.1), due to the influence of various factors, shoreline changes of the typical headland-bay sandy beaches have been very severe recently. This paper will apply three static headland-bay beach models as well as our proposed elliptical model to analyze four typical headland-bay beaches in the study area to test the applicability of these four models to this area. We adopted the static headland-bay beach concept to explain the recent dynamic evolutionary characteristics of the coast.

2 Study Area

Laizhou Bay is located on the north of Shandong Peninsula and is part of the Bohai Sea. Since the post-glacial period, the sea level has risen gradually, and land on the east coast of Laizhou Bay has been submerged. A sandbar- lagoon coast has developed from Longkou Port to Diao- longzui (Xu, 1989; Zhuang., 1989), and the coastlinesof Longkou Port-Shihuzui, Shihuzui-Haibeizui, Hai-beizui- Sanshan Island, and Sanshan Island-Diaolongzui headlandbays have formed. The headland is composed of protero- zoic quartzite, granodiorite, and Yanshan granite (Fig.2).

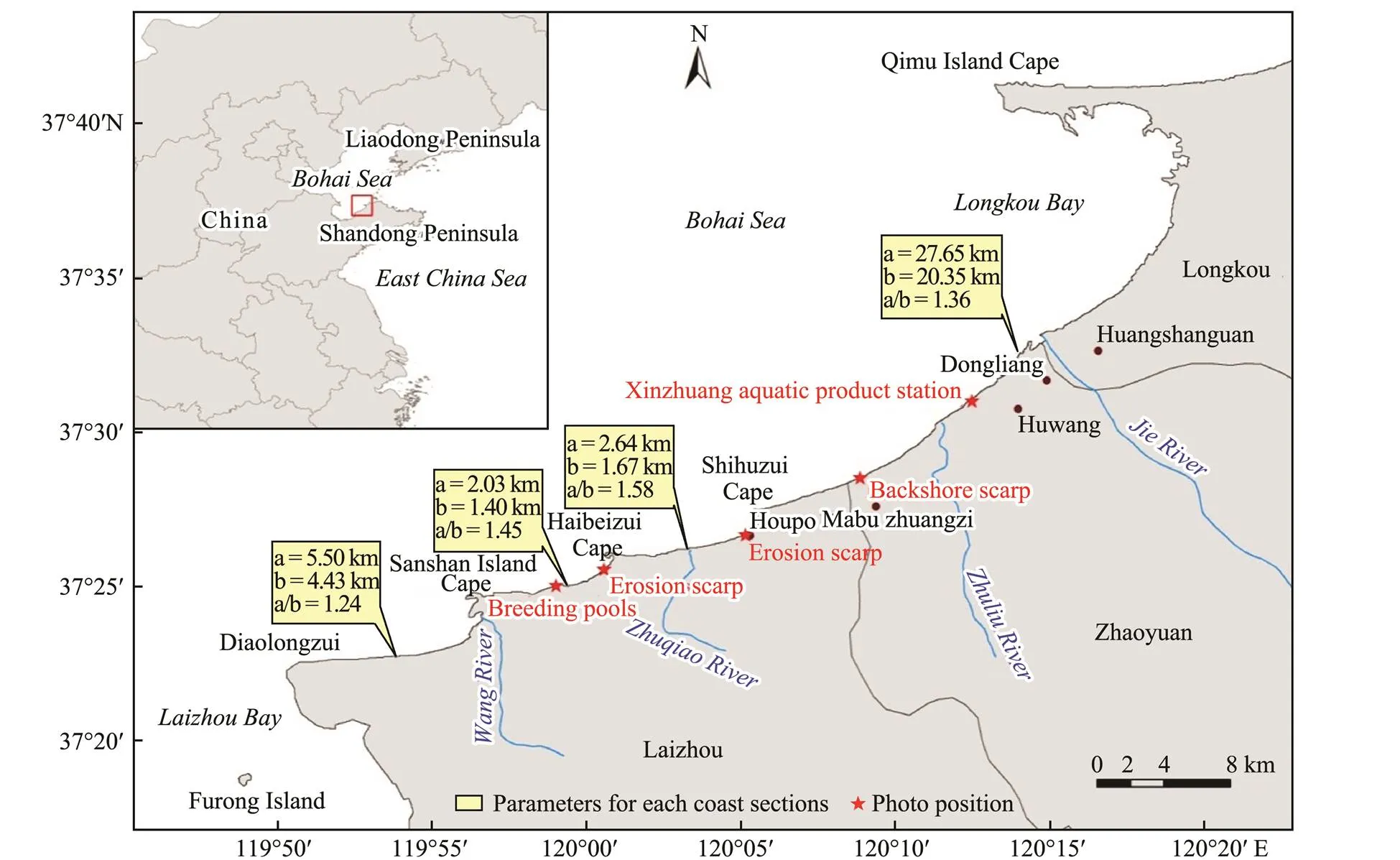
Fig.1 Location map of the study area.

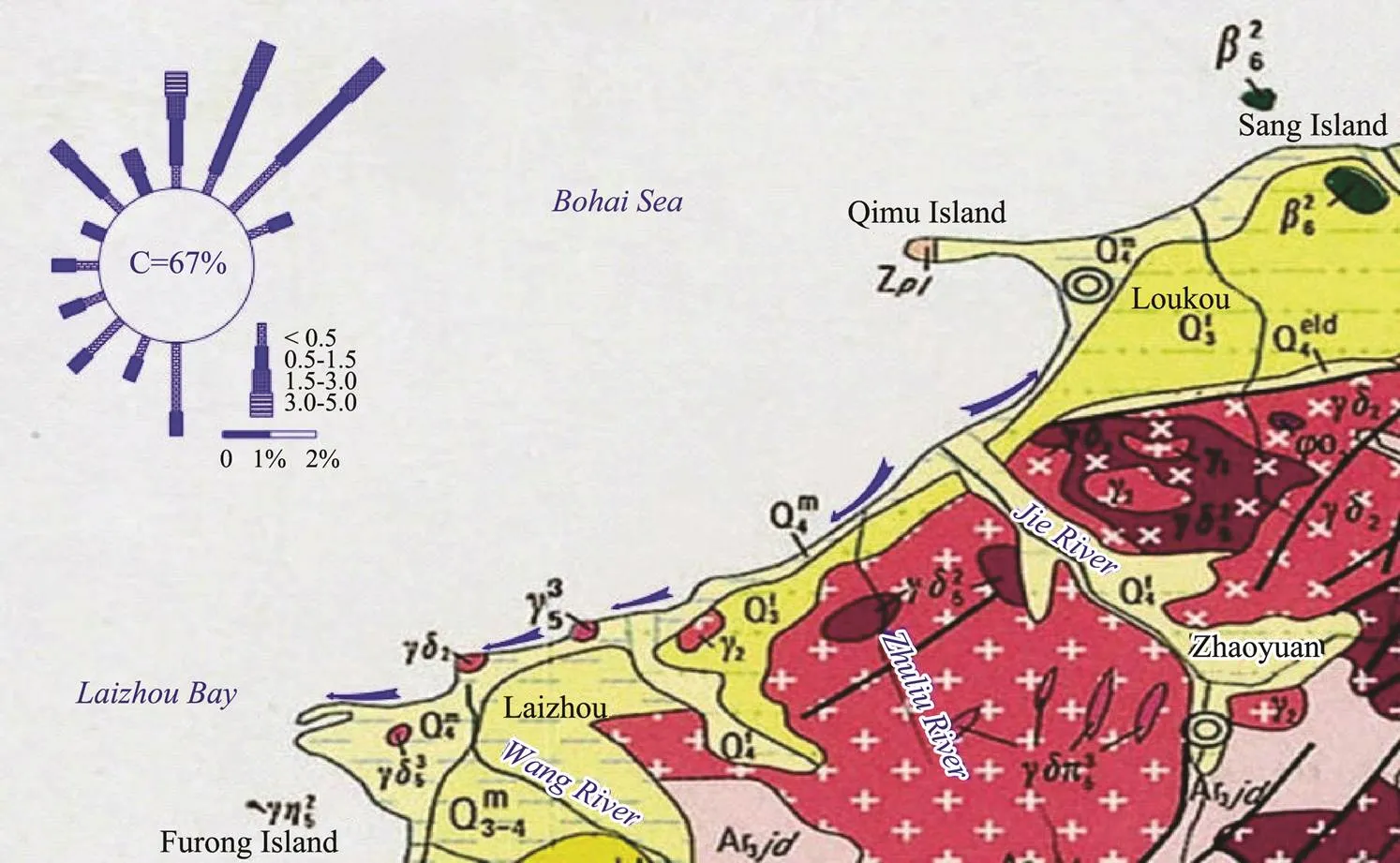
Fig.2 Geologic map of the east coast of Laizhou Bay (modified from the Geological Atlas of China).

The waves in the research area are mainly wind waves. Their occurrence frequency is greater than 80%. The sea area around Sanshan Island is dominated by northward waves. The direction of both the strong waves and the normal waves is NNE, the average wave height is 1.3m, and the average wave period is 4.9s. In the sea area of Longkou Port, the direction of both the strong waves and the normal waves is NE, while the direction of the subnormal waves is NNE. The average wave height is 1.23m, and the average wave period is 4.3s (CCRBC, 1991). The mean tidal range of Sanshan Island is 1.00m, and the mean tidal range of Longkou Port is 0.9m. The east coast of Laizhou Bay is a microtidal coast with irregular mixed semi-diurnal tides (Chang., 1993).

According to Chang. (1993), this area is divided into two sections based on the sediment transport pattern. From the Jie River to Longkou Port, sediment is transported towards Longkou Bay, while from the Jie River to Diaolongzui, sediment is transported towards the southwestern coast (Fig.2). Waves control the overall trend of coastal sediment transport. The river normally has an important influence on local coastal sediment transport. For example, the sediment supply from the Jie River has almost ceased now. However, because of the long-term se- diment discharge into the sea, the river mouth delta protrudes into the sea,., the shoreline is significantly convex to the sea, and the massive sand deposits have become the sand source for the longshore transport of sedi-ment. Thus, this area suffers intense erosion.

3 Methods

In this paper, by conducting field investigations, comparing our observation results with historical data, and adopting model calculations and analysis, we studied the current evolutionary stage of the beaches in the study area. The field investigations included field reconnaissance, recording erosion or deposition phenomena occurring on the beaches, and taking pictures to record observations while using DGPS for positioning. The historical data on the evolution of the study area was compiled and compared with the new field data to assess any trends in the recent evolution of the beach. Finally, the mathematical models were used to simulate the morphology of the headland-bay beaches in this area and predict the static equilibrium position of the shoreline.

3.1 Common Models of Headland-Bay Beaches

In this study, three existing static equilibrium headland- bay beach models were applied, including the logarithmic spiral model, the parabolic model, and the hyperbolic tangent model. These three models are described in Table 1.

Table 1 Static equilibrium headland bay model

3.2 Elliptical Model

There are advantages and disadvantages for the headland-bay beach models described in the previous section. Taking into consideration the fact that the influence range of the wave diffraction on the headland point of the beach is limited and that the location of the down-drift control point is fixed, we developed the elliptical model to simulate a static headland-bay beach (Li, 2013). The mathematical equation for this model is:

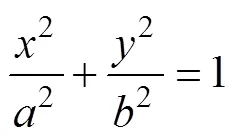
As seen in Fig.3, there are three parameters in this model:is the length of the semi-major axis,is the length of the semi-minor axis,., the distance from the diffraction point to the straight part of the beach, andis the semi-focal length. There is a specific physical meaning forin this model: the focus of the ellipse is the headland point and is also is the diffraction point of the incident wave. In a headland bay beach without sand supply, the shape of the wave crestline is the circumference of the elliptical model and it is also the coastline of a static equilibrium beach.

Fig.3 Sketch of the elliptical model.

For this model, the equilibrium shape of the headland- bay beach can be determined by obtaining the values ofandand the orientation of the wave crest line. The orientation of the wave crest line corresponds to the direction of the mean wave energy flux at the control point area (González and Medina, 2001). The value ofcan be obtained from maps, charts, satellite images, or aerial pho- tographs. By assuming that there is a correlation betweenandequilibrium shape of the headland-bay beach can be drawn once the correlation coefficient is determined.

Through field investigations and remote sensing image analysis, the values ofandfor 15 headland-bay beaches on the north coast of the Shandong Peninsula were obtained using curve-fitting and the elliptical model. Based on the data for 10 headland-bay beaches, there is an approximate linear correlation betweenand, and the ratio oftois approximately 1.24 (Fig.4). For the other 5 headland-bay beaches, which are not in an equilibrium state or in dynamic equilibrium, the ratio is much higher than 1.24 (Li, 2013).

Fig.4 The correlation between a and b in elliptical model (modified from Li, 2013).

4 Results and Discussion

4.1 Simulation Results

The four arc-shaped bays on the east coast of Laizhou Bay are all large bays. Chang. (1993) were the first to use the logarithmic spiral bay theory to study shoreline erosion in this area. They predicted the future position of the coast and suggested implementing the headland control engineering to prevent further erosion. Chen. (2007) concluded that Longkou Bay is a typical logarithmic spiral bay, and due to the shielding effect of Qimu Island, the bay is formed in a wave shadow area. The area to the west of Haidai town is affected by strong waves coming from the NW, and thus the sediment mainly moves laterally. Hydrodynamic conditions have ensured the stability of Longkou Bay, and a logarithmic spiral bay eventually developed. Feng. (2009) studied Longkou Bay using the parabolic model and predicted the changes that would occur to the coastline.

The above studies all performed qualitative analyses to the beaches in this area, but as they abided by fixed models, the applicability of the models themselves remains to be verified. We determined the plane morphology of the beach and its evolutionary trend through comparative analyses of several models and simulation calculations. Based on the four models described above, the four headland bays in the area were simulated (the area from Sanshan Island to the Diaolongzui coast is simulated with and without port construction), and the parameters for each model were obtained and are listed in Table 2.

4.2 Result Analysis

Simulation results are markedly different from those of the real shoreline in the study area, indicating that the logarithmic spiral model cannot be successfully applied to this shoreline. On the coast from Sanshan Island to Diao- longzui, which is almost in equilibrium, the relatively straight shoreline and the bending coastal segments with small curvature differ slightly from the simulation results. However, the shield section close to the headland is completely different. The remaining three coastal segments are in disequilibrium, so the simulation results differ more from the real coastline. On the shielded coastal segments the real coastal line and the simulation results are not consistent, and on the coastal segments that are almost straight the real costal line differs significantly from the simulation results as well. The simulated coastline migrates inland. Rea and Komar (1975) point out that the simulation curvature can be adjusted to closely fit the real coastline only by moving the position of the center of the model, but if this is done, the parameters of the model have no definite physical meaning.

The simulation results of the hyperbolic tangent model are consistent with the real coastline for those sections of straight or arc-shaped with a small curvature. The results for the section closest to the headland are inconsistent, but the model can simulate a headland-bay beach in static or dynamic equilibrium. Even for headland-bay beaches not in equilibrium, the simulation results of the model are consistent with the real shoreline. In addition, the starting point of the simulated headland bay does not coincide with the wave diffraction point, and it cannot accurately depict the relationship between the coastline shape and the wave direction. Three of the parameters also have no special physical meaning. It is more suitable to use the hyperbolic tangent model to simulate a coastline influenced by the groin or tombolo formed by the effects of offshore break- waters. Moreno and Kraus (1999) argued that for a coast in equilibrium, the product of parametersandis 1.2, andis 0.5. Oliveira and Barreiro (2010) demonstrated that the product of parametersandis about 0.87. In this study, the product ofandfor the four headland- bay beaches studied was greater than 1.2, andwas not always 0.5, so the hyperbolic tangent model cannot satisfactorily explain the shoreline changes in the study area.

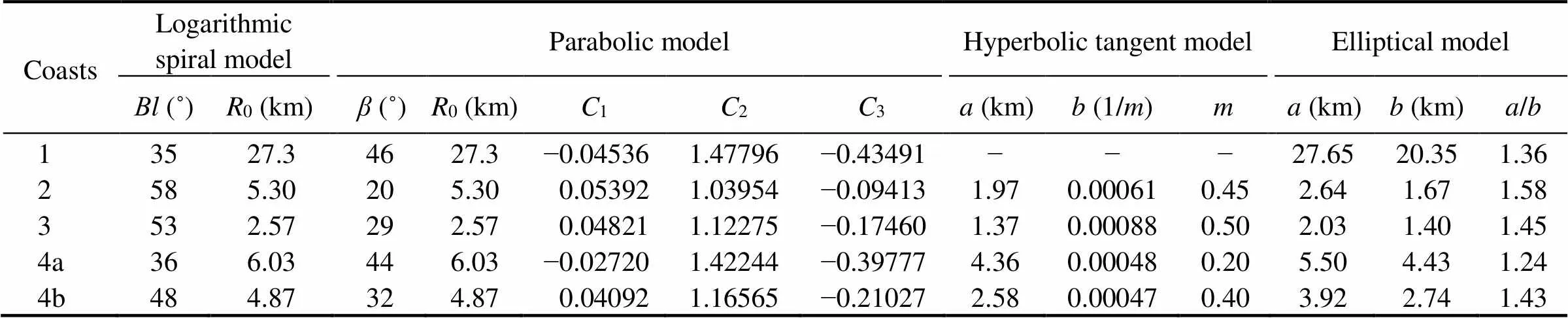
Table 2 Parameters for various models on the east coast of Laizhou Bay

Notes: 1, Longkou Port-Shihuzui; 2, Shihuzui-Haibeizui; 3, Haibeizui-Sanshan Island; 4a, Sanshan Island-Diaolongzui (with port construction); 4b, Sanshan Island-Diaolongzui (without port construction).

The parabolic model was proposed some time ago and has been widely used. This model is included in the Coastal Engineering Manual of the United States. The MEPBAY software developed by Vale University in Brazil (Klein., 2003) uses the parabolic model to simulate headland-bay beaches. The many advantages of the model make it easy to use. These advantages include the following: the control point coincides with the wave diffraction point, the wave crest line is parallel to the straight coastal segments, and the related parameters are obtained from the angle between the wave crest line and the control line. By simulating the four headland bays in the study area, we determined that the parabolic model results are consistent with the real shorelines at their present evolutionary stage. For the Sanshan Island-Diaolongzui coastal segment, model results are consistent with the real shoreline. Since the rest of the headland bays are in disequilibrium, the simulation results all migrate toward the land, which indicates that in the future the coast will still be eroded. However, the down-drift control point of the parabolic model is not easy to be determined. The chosen down-drift control point exerts some influence on the result of the equilibrium headland-bay beach simulation, and it exerts more influence on the result of the disequilibrium and dynamic equilibrium headland-bay beach simulations.

The simulation results of the elliptical model fit better with the actual coastline than the results of the other models (Table 1). The ratios oftofor most of the headland- bay beaches are larger than 1.24, and only the coast from Sanshan Island to Diaolongzui has a ratio of about 1.24. Based on our field investigations, we conclude that almost all of the coastal segments are being eroded, except for the Sanshan Island-Diaolongzui and Sanshan Island- Diaolongzui segments, which will be in disequilibrium if there is no port construction.

4.3 Application of the Elliptical Model

4.3.1 Analysis of the evolutionary trend of the beach

The results of the elliptical model indicate that most of the coastal segments on the east coast of Laizhou Bay are being eroded, and some of the coastal segments are far from being in equilibrium.

In the Longkou Port-Shihuzui coastal segment, the most significant erosion is occurring between the mouth of the Jie River and the mouth of the Zhuliu River (Feng., 2009). Due to the influence of long-term sediment discharge from these rivers, the coastline in this area protrudes significantly into the sea, making it be eroded strongly (Fig.5).

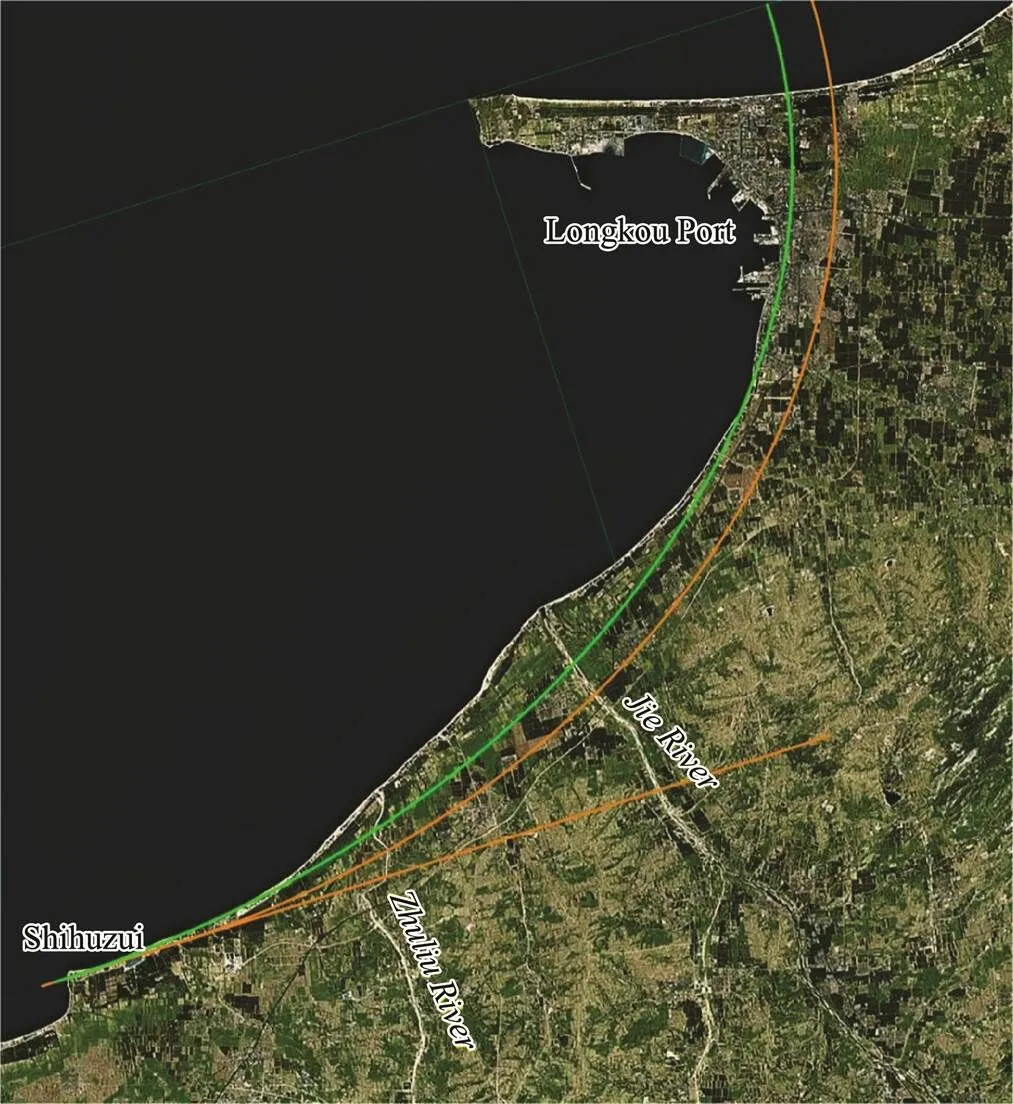
Fig.5 Simulation result for the Longkou Port-Shihuzui coast. Green line is the result of curve-fitting; Orange line is the location of the equilibrium coastline.

The simulation result shows that the location of the coastline segments in equilibrium will migrate toward the land, and to some extent, the sediment transport from the Jie River mouth will maintain the unbalanced state on both sides of the river mouth. The sediment transport calculation results for this coastal segment also indicate that at the mouths of the Jie and Zhuliu Rivers and in other places, the directions of net sediment transport all point toward Longkou Port and Shihuzui. Based on the data of hydrological station, before the 1950s, sediment discharge from the rivers,., about 500000 tons per year for the Jie River, was sufficient to maintain the stability of the shoreline or to build it up slightly. Now, the sediment discharges from many rivers on the east coast of Laizhou Bay (including the Jie River and Zhuliu River) are negligible, and the shoreline erosion is inevitable.

The coast from behind Houpo Village to the southwest of Shihuzui (Fig.6b) and the coast to the southwest of Haibeizui (Fig.7b) have been eroded. These two locations are both in the shield section of the headland bay. The causes of the erosion are also the same, as shown in Figs.6 and 7. According to the Static Equilibrium Bay Concept, the stable coastline will eventually retreat toward the land, and the previous longshore sediment transport keeps the shoreline to be in dynamic equilibrium. When the longshore sediment transport decreases or completely ceases, wave diffraction and refraction can still generate the along- shore current. The sediment is transported downstream, and the bay gradually transform from a state of dynamic equilibrium to a state of static equilibrium. Compared with the straight shoreline segments, adjustment and erosion of the coastal segments in the shield area are more obvious.

Fig.6 (a) Simulation results for Shihuzui shoreline in static equilibrium. (b) Erosion escarpment behind Houpo Village.

Fig.7 (a) Simulation results for the Haibeizui shoreline in static equilibrium. (b) Erosion scarp to the southwest of Haibeizui cape.

The Sanshan Island-Diaolongzui coastal segment was previously eroded. Monitoring results from the 1980s in- dicate that the erosion rate was 2myr−1and the eroding only occurred at Diaolongzui, which is located at the end of this coastal segment where there was slight siltation (Zhuang., 1989). Now, the construction of Sanshan Island port has changed the trend in coastal evolution. The terminal on the east side of Sanshan Island blocks the westward longshore sediment transport. The sediment fromthe upstream coastal segments will eventually be deposited on the east side of the wharf and the coast will gradually reach a new equilibrium (Fig.8). On the west side of San- shan Island, the sediment supply is completely blocked by the dock wharf, and because the harbor basin extends out into the sea, a new wave diffraction point has formed (upstream headland). Based on our simulations, we conclude that after a long period of adjustment, the current coastline is basically in equilibrium (green line in Fig.8). Based on our field investigations, we determined that the beach is relatively stable, which also proves that the new headland can protect the downstream area. In addition, for a case without a port in the past, the simulation of Sanshan Island beach revealed that the overall shoreline (in static equilibrium) migrated toward the land (orange line in Fig.8), and the amount of erosion was around 240m at the bay head (Section P–P’).

4.3.2 Current evolutionary trend of the sandy beaches

Since the middle of the last century, especially since the 1980s, the beaches on the east coast of Laizhou Bay have experienced severe erosion.

Based on the field investigations in the 1980s, Chang(1993), found that the base of the backwall at the Xinzhuang Aquatic Product Station had suffered erosion (Fig.9a). By 2010 (30 years later), 80m of beach was washed away to the north of the aquatic station. The aquatic station had been completely destroyed, and one side of the house had collapsed. The wave-eroded scarp behind the house was over 2m high (Fig.9b).

Fig.8 Simulation results for the Sanshan Island-Diaolongzui Shoreline. Green line is the simulation result as the corner point of Sanshan Island harbor is the updrift control point; Orange line is the simulation result as the rocky cape of Sanshan Island is the updrift control point.

Fig.9 Pictures of the Xinzhuang aquatic product station. (a), taken in May 1981, by Zhuang Zhenye; (b), taken in May 2010, by Li Bing.

During the 1980s, some of the coastal segments in the study area were being eroded and some were accreting(Chang., 1993), while at present, widespread erosion and retreat are occurring. Eroded scarps can be easily seen in the Longkou Port-Shihuzui Coastal Segment, such as at Huangshanguan, behind Dongliang Village, to the north of Zhaishang Village, and to the north of Huwang Village. In many places, most of the weakly protected projects have been destroyed by waves. Especially to the north of Mabuzhuangzi, the coastline is approaching the back walls of village houses, and wave erosion behind the houses has formed a 4-m high steep cliff. The beach there has been eroded down by at least 3m, and the houses are partially suspended (Fig.10). From Shihuzui to Haibeizui, the erosion is also strong. Especially to the north of Houpo Village, the underlying lagoon sediments of the beaches are exposed, and a 5-m high erosional escarpment has formed (Fig.6b). From Haibeizui to Sanshan Island, the beach has also been heavily damaged, and erosion scarps are common (Fig.7b). Due to the influence of the revetment, along some coastal segments the beach surface barely has any sand. From Sanshan Island to Diaolongzui, there are many culture ponds, and the coastline is basically in a fixed state.

近年来，碳减排政策逐渐成为企业生产运营中的关键制约要素，影响到企业生产的各项活动。本文以高能耗、高碳排放的高炉炼铁生产为对象，对碳限额与交易政策影响下的多配方—多铁种高炉炼铁多周期生产计划问题进行了研究。考虑了碳限额与交易政策下周期性碳约束和累计碳约束两种情形，采用模块建模的方法，构建了两种碳约束下多配方—多铁种高炉炼铁生产计划MILP模型，并基于该模型对所研究的问题进行了数值分析。通过数值分析，一方面验证了模型的有效性和高效性,另一方面探讨了两种碳约束下动态碳价对企业生产计划的影响、碳限额对生产总成本的影响、动态碳价对碳排放量的影响。

Fig.10 Backshore scarp behind Mabuzhuangzi.

4.3.3 Causes of erosion

There are many potential causes for shoreline erosion, and on the east coast of Laizhou Bay, the main cause is the reduction in river sediment transport and poorly planned sand excavation (Li., 2013).

Many of the rivers in the Shandong Peninsula are seasonal mountain rivers with short lengths. Over a long period of time, river sediment transport has played an important role in shaping the Shandong coast. According to the previous studies, the annual sediment transport flux of the main rivers in the study area is estimated to be 150–200 million tons. Due to reservoir construction, a large amount of river sediments are intercepted and do not reach the estuarine and coastal areas. In addition, the runoffs of these rivers are also significantly reduced. Many rivers have almost been cut off,., the Yellow River, Jie River, and Zhuliu River.

Sand mining is also an important reason for shoreline erosion and retreat. On the northern Shandong Peninsula, sand mining was once widespread. The direct excavation of sand from the beach surface or from the nearshore area destroys the equilibrium of the beach system. Based on the theory of equilibrium beach profiles, the beach profile will reach a new equilibrium due to the influence of transverse sediment transport. As a result, sediments on the beach enter the sea, and the shore is eroded. According to statistics made by one of the authors of this paper, large- scale sand mining and outward transport of sediment began to increase in the early 1980s (Zhuang., 1989). There are laws and regulations prohibiting sand excavation, but the sand mining of beach surfaces frequently occurs. To the west of the Zhuliu River, on the backshore of the beach north of Laodian Village in Zhaoyuan, a sand excavation pit with tens of meters wide and more than 100m long can still be seen now, as well as a destroyed shelter forest. In the coastal segments from Shihuzui to Sanshan Island, a large number of culture ponds have been built on the beach. The excavation of culture ponds directly destroys the beach (Fig.11), and it is difficult for the beach to recover from this damage. Nearshore sand excavation cannot be stopped despite being banned, and it has caused serious consequences along the nearby coast (Xu., 2010). At present, sand mining ships still secretly excavate sea sand hundreds of meters away from the coast.

Fig.11 The picture that shows breeding pools destroyed theshoreline structures.

Since the river sediment supply is almost exhausted and sand mining cannot be stopped completely, according to our model, in the study area on the east coast of Laizhou Bay, the original stable coastal segments being and been eroded will suffer more serious erosion. The model also suggests that most of the beaches in the area (except the Sanshan Island-Diaolongzui coastal segment) will remain in an erosive state and retreat for a long period of time. Natural adjustments will continue until static equilibria of the headland-bay beaches are achieved.

5 Conclusions

In this paper, three common models (the logarithmic spiral model, the parabolic model, and the hyperbolic tangent model) were used to simulate four typical headland-bay beaches on the east coast of Laizhou Bay. Combined with field investigations, these models were used to analyze the equilibrium state of the beaches.

The simulation results of the logarithmic spiral model are not consistent with the features of the four bays. The hyperbolic tangent model can simulate almost all of the headland-bay beaches, whether they are in equilibrium or disequilibrium. The parabolic model has been widely used because of its advantages, and the simulation results are fairly accurate, but it is difficult to determine the down- drift control point. The elliptical model satisfactorily si- mulates static headland-bay beaches, and it is easier to use than the other models.

The simulation results reveal that, except for the Sanshan Island-Diaolongzui coastal segment, the other three simulated shorelines of the bay migrate toward the land, which is consistent with the current coastal erosion that is occurring. The buildings on the shore have a certain influence on the shoreline simulation.

Currently, on the east coast of Laizhou Bay, almost all of the headland-bay beaches are subject to intense erosion, except for the Sanshan Island-Diaolongzui coastal segment, and there is a growing serious trend. Based on these simulations, we conclude that erosion in the bay is especially severe and the beaches are far from an equilibrium state. The previous dynamic equilibrium maintained by coastal sediment transport and river sediment transport has been disrupted. The beaches will transform from dynamic equilibrium to disequilibrium, and eventually, they will evolve toward static equilibrium.

Acknowledgements

CCRBC (Compilation Committee of ‘Records of Bays in China’),1991.. Ocean Press, Beijing, 1-136.

Chang, R. F., Zhuang, Z. Y., and Wu, J. Z., 1993. Retrogression and protection of the northwest coast of the Shandong Peninsula., 23 (3): 60-68.

Chen, Z. S., 1999. Seasonal variability of sand transport trends and distributions of wave energy flux in a beach between headlands., 18 (3): 41-48.

Chen, Z. S., Wang, W. H., and Wu, S. Y., 2007.Ocean Press, Beijing, 1-583.

Dai, Z. J., 2004. Application of judgment rules for log-spiral coast to arc-shaped shoreline in South China., 23 (3): 43-49 (in Chinese with English abstract).

Feng, X. L., Dong, W. W., Zhuang, Z. Y., Wang, Y. J., and Chen, Z. H., 2009. The calculation of alongshore silt discharge rates and evolution development in the east coast of Laizhou Bay., 39 (2): 304-308 (in Chinese with English abstract).

González, M., and Medina, R., 2001. On the application of static equilibrium bay formations to natural and man-made beaches., 43 (3): 209-225.

Halligan, G. H., 1906. Sand movement on the New South Wales coast., 31: 619-640.

Hsu, J. R. C., and Evans, C., 1989. Parabolic bay shapes and applications., 87 (4): 557-570.

Hsu, J. R. C., Uda, T., and Silvester, R., 2000. Shoreline protection methods–Japanese experience. In:. McGraw-Hill, New York, 1-77.

Klein, A. H. F., Vargas, A., Raabe, A. L. A., and Hsu, J. R. C., 2003. Visual assessment of bayed beach stability using computer software., 29: 1249-1257.

Krumbein, W. C., 1944. Shore processes and beach characteristics. In:. Beach Erosion Board, Washington, D. C., 1-47.

Li, B., 2013. Evolution research of sand coast on the north of the Shandong Peninsula. PhD thesis. Ocean University of China.

Li, B., Zhuang, Z. Y., Cao, L. H., and Du, F. C., 2013. Countermeasure research on erosion and protection of the sandy coast, Shandong Province, China., 81 (2): 31-40.

Li, Z. L., and Chen, Z. S., 2006. Equilibrium shape model of headland bay and application in South China coasts., 25 (1): 123-129.

Li, Z. L., and Chen, Z. S., 2007. Progress in studies on the equilibrium shape of headland-bay shoreline., 9 (1): 74-83.

Li, Z. L., Li, W. Q., Chen, Z. S., and Zhu, Y. M., 2014. Influencing factors and classifications of arc-shaped coasts in South China., 69 (5): 595-606.

Moreno, L. J., 1997. Critical review of the headland-concept of shore protection. Master thesis.College Station, A&M University.

Moreno, L. J., and Kraus, N. C., 1999. Equilibrium shape of headland-bay beaches for engineering design.. American Society of Civil Engi- neers, New York, 860-875.

Oliveira, F. S. B. F., and Barreiro, O. M., 2010. Applications of empirical models to bay-shaped beaches in Portugal., 57: 124-131.

Rea, C. C., and Komar, P. D., 1975. Computer simulation models of hooked beach shoreline configuration., 45: 866-872.

Silvester, R., 1970. Growth of crenulate shaped bays to equilibrium., 96 (2): 275-287.

Tan, S. K., and Chiew, Y. M., 1994. Analysis of bayed beaches in static equilibrium., 120 (2): 145-153.

Xia, Y. M., 1988. The curve of the plan outline of sandy bay in equilibrium., Beijing, 341-352.

Xu, J. S., 1989. Development of sand bar-lagoon and evolution of the coastline in the northern part of Shandong Peninsula at the late Holocene epoch., 7 (4): 25-31.

Xu, Z. J., Zhang, X. L., and Zhang, C. H., 2010. Coastal erosion in Shandong Peninsula and Yellow River Delta and related countermeasures., 28 (10): 90- 95.

Yang, Y. X., and Zhang, J. B., 2007. Static equilibrium headland bay coast theory and its application to coasts of the Yellow and Bohai Seas., 26 (2): 38-46.

Yasso, W. E., 1965. Plan geometry of headland bay beaches., 73: 702-714.

Yu, J. T., and Chen, Z. S., 2010. Study of headland-bay sandy coast stability in South China., 28 (2): 110-116.

Yu, M. J., Chen, S. X., and Hsu, J. R. C., 2004. Reinspection on the precision of static equilibrium headland bay beach empirical equation.. Taipei, 617-622.

Zhuang, Z. Y., Chen, W. M., Xu, W. D., and Shen, C. L., 1989. Retrogression of straight sandy beaches in the Shandong Peninsula and its results.,19 (1): 90-98 (in Chinese with English abstract).

May16, 2018;

August 23, 2018;

January 2, 2019

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2020

. E-mail: hardyqd@ouc.edu.cn

(Edited by Chen Wenwen)