Contribution of Mesoscale Eddies to the Subduction and Transport of North Pacific Eastern Subtropical Mode Water

YANG Zhitong, and LUO Yiyong

Contribution of Mesoscale Eddies to the Subduction and Transport of North Pacific Eastern Subtropical Mode Water

YANG Zhitong, and LUO Yiyong*

Physical Oceanography Laboratory/CIMST, Ocean University of China and Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, China

This study investigates the contribution of mesoscale eddies to the subduction and transport of North Pacific Eastern Subtropical Mode Water (ESTMW) using the high-frequency output of an eddy-resolved ocean model spanning the period 1994–2010. Results show that the subduction induced by mesoscale eddies accounts for about 31% of the total subduction of ESTMW formation. The volume of ESTMW trapped by anticyclonic eddies is slightly larger than that trapped by cyclonic eddies. The ESTMW trapped by all eddies in May reaches up to about 2.8×1013m3, which is approximately 16% of the total ESTMW volume. The eddy-trapped ESTMW moves primarily westward, with its meridional integration at 18˚–30˚N reaching about 0.17Sv, which is approximately 18% of the total zonal ESTMW transport in this direction, at 140˚W. This study highlights the important role of eddies in carrying ESTMW westward over the northeastern Pacific Ocean.

mesoscale eddies; subduction; transport; North Pacific Eastern Subtropical Mode Water

1 Introduction

Mode water is a distinct water mass characterized by low potential vorticity (PV) and a thermostad in the main thermocline. It is formed by deep winter mixed layers mainly due to strong convective mixing and can be traced over wide areas of the subtropical gyres by using the low-PV signature (McCartney, 1982; Talley and Raymer, 1982). Three major mode waters have been identified in the North Pacific: Western Subtropical Mode Water (WSTMW;Masuzawa, 1969), Central Mode Water (CMW; Nakamura, 1996; Suga, 1997), and Eastern Subtropical Mode Water (ESTMW; Hautala and Roemmich, 1998). ESTMW is centered at (30˚N, 140˚W) with a temperature range of 16–22℃ and a density range of 24.0–25.4σ(Hautala and Roemmich, 1998). As part of the Subtropical Cell trans- porting heat and salt from the subtropics to the tropics in the North Pacific, the ESTMW is subducted into the thermocline, swept westward by the North Equatorial Current, and reaches the equatorwestern boundary currents and their interior pathway. The subsurface water then flows into the eastward Equatorial Undercurrent, up- wells in the eastern equatorial Pacific Ocean, and eventu- ally flows out of the tropics (McCreary and Lu, 1994).

Mesoscale ocean eddies strongly influence ocean cir- culation and climate by transporting and stirring momen-tum and tracers, such as heat, salinity, and CO2, along density surfaces (Bryden and Brady, 1989; McGillicuddy, 2007; Chelton, 2011a; Dong, 2014; Zhang, 2014). The effects of mesoscale eddies on mode water formation and transport have been widely studiedobservations and models of the western and central regions of the North Pacific. Anticyclonic eddies in deep mixed layers have been found to contribute sub- stantially to the formation and transport of WSTMW (Uehara, 2003; Pan and Liu, 2005). Satellite-derived sea surface height anomalies and Argo profiling float data indicate that WSTMW is mainly trapped and transported by anticyclonic eddies (Kouketsu, 2012; Liu and Li, 2013). Using a high-resolution ocean general circulation model (OGCM), Qu(2002) found that eddies en- hance the annual subduction rate of WSTMW and CMW by about 34% of the total subduction. Nishikawa(2010) pointed out two possible processes as causes of eddy subduction: 1) destruction of the PV gradient by eddy mixing and 2) southward translation of anticyclonic eddies accompanying low PV. Eddies may broaden the horizontal extent of the subduction zone, and the PV is asymmetric outside the anticyclonic eddy core, with en- hanced subduction near the southeastern rim of the anti- cyclonic eddy (Xie, 2000; Xu, 2014, 2016). Therefore, existing studies show that mesoscale eddies play a dominant role in the subduction and transport of mode waters in the northwestern North Pacific.

Existing studies have mainly focused on the formation mechanism, dissipation, and climate-related variability of ESTMW in the North Pacific. ESTMW is formed through preconditioning of the winter mixed layer (Hautala and Roemmich, 1998; Toyoda, 2004) or a small density advection mechanism (Hosoda, 2001). The main factors driving rapid dissipation are vertical mixing in the lower ESTMW layer and modulation in the upper EST- MW layer due to less heat input in warmer seasons (Su- gimoto and Hanawa, 2007). Toyoda(2011) sug- gested that the interannual variability of ESTMW is due to the Ekman convergence of saline water, summer ther- mal stratification, and winter surface cooling. Mixed layer depth (MLD) anomalies in the formation region of ESTMW are negatively correlated with the Pacific De- cadal Oscillation index at the interannual and decadal time scales (Toyama, 2015; Toyoda, 2017). Luo(2009) found that global warming induces sig- nificant reductions in ESTMW volume. However, the effect of mesoscale eddies on ESTMW has not been re- ported. In this study, we investigate the characteristics of mesoscale eddies in the eastern subtropical North Pacific and evaluate their contribution to the subduction and transport of ESTMW by analyzing the high-frequency output of a fine-resolution OGCM. The rest of this paper is organized as follows. Section 2 describes the model and observational data used in this study. The methodol- ogy of eddy identification and eddy-trapped transport calculation is also introduced in this section. Section 3 verifies the model output against actual observations. Section 4 presents the mean fields of ESTMW. Section 5 investigates the impact of mesoscale eddies on the sub- duction and transport of ESTMW. Section 6 summarizes our findings.

2 Data and Methods

2.1 Model Output

The output of an eddy-resolved OGCM for the Earth Simulator (OFES) (Masumoto, 2004; Sasaki, 2008), which is based on the third Modular Ocean Model (MOM3), is used for our analysis. The OFES model ex- tends from 75˚S to 75˚N with a horizontal grid spacing of 1/10˚ in both latitude and longitude; it has 54 vertical levels with resolutions of 5m near the surface and 330m near the maximum depth of 6065m. The model has three simulations; in this work, the simulation we use is initial- ized from a state of rest with the annual mean temperature and salinity of the World Ocean Atlas 1998 (WOA98) and spun up for 50 years with monthly climatological forcing from the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) reanalysis (Kalnay, 1996). After spin-up integration, hindcast simulation is conducted with daily atmospheric forcing from NCEP/NCAR reanalysis. Details of the modeland simulation can be found in Sasaki(2008). Three-day model snapshots spanning the period 1994–2010 were downloaded from the Asia Pacific Data Research Center (http://apdrc.soest.hawaii.edu/dods/public_ofes/OfES/ncep_ 0.1_global_3day/). Our study focuses on the eastern sub- tropics of the North Pacific, which is the main area of ESTMW.

2.2 Observational Data

In this study, two observational datasets are used to validate the OFES output. The monthly fields oftemperature and salinity are provided by theData Analysis System (ISAS; Gaillard, 2009). The ISAS tool was designed to map Argo profiles and a few other CTD observations, including marine mammals and moor- ing, by using an optimal interpolation algorithm. Two typical interpolation scales were used to map the data (Kolodziejczyk, 2018): the first scale is 300km, which is consistent with the nominal sampling target of the Argo network, and the second scale is four times the local radius of deformation. We use the latest release of the ISAS products for the period 2002–2015, also called ISAS15 (Kolodziejczyk, 2017), which are computed on a grid with a 0.5˚×0.5˚ horizontal resolution and 152 vertical levels from the surface to 2000m.

The daily sea level anomaly (SLA) provided by the Archiving Validation and Interpretation of Satellite Data in Oceanography (AVISO; www.aviso.altimetry.fr) is also used to evaluate model mesoscale eddy statistics and eddy kinetic energy (EKE) in this study. The processing and distribution of this product is conducted by the Euro- pean Copernicus Marine Environment Monitoring Ser- vice, which has a spatial resolution of 1/4˚×1/4˚ Cartesian grid with a synchronous time period of model simulation from 1994 to 2010.

2.3 Eddy Identification and Eddy-Trapped Transport Calculation

Mesoscale eddies are detected using the algorithm de- veloped by Faghmous(2015); here, eddies are de- fined as the outermost closed-contour SLA containing a single extreme (maximum/minimum). The local maximum and minimum for an eddy over a 5×5 neighborhood are first detected. Then, the eddy boundary is obtained by iteratively proceeding upward (downward) for an anti- cyclonic (cyclonic) eddy around the extrema using an increment of 0.25cm until a closed SSH contour that sat-isfies several criteria is found. Here, one criterion is that only one local maximum (minimum) must exist for an anticyclonic (cyclonic) eddy. The center of an eddy is defined as the SSH-based centroid. The amplitude of an eddy is defined as the difference between the extremum SSH and the SSH along the eddy boundary. The radius scale of an eddy is defined as the mean distance from the eddy center to the maximum geostrophic velocity.

Based on Zhang(2014), the eddy-trapped zonal ESTMW transport is defined asC, whereis the eddy-trapped STMW volume andCis the zonal propa- gation speed of the eddy. We set up an average bin with a 1˚ meridional width and 1˚ zonal length. Then, the aver- aged eddy-trapped zonal ESTMW transport across the 1˚-latitude section is calculated by:

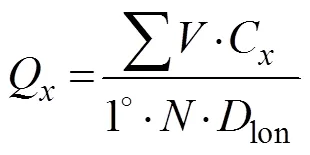
wherelonis the zonal length of each grid point andis the number of snapshots. The averaged eddy-trapped me- ridional ESTMW transport across the 1˚-longitude sectionQis defined as:

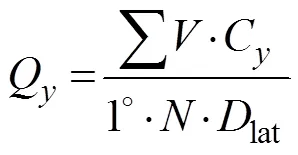
whereCis the meridional propagation speed of the eddy,latis the meridional length of each grid point, andis the number of snapshots.

3 Verification of the Model Simulation

Before exploring the dynamic process of subduction and transport by OFES simulation, the model must be validated against actual observations. Fig.1 compares the results of climatological winter MLD and density be- tween the model and observations. The MLD is defined as the depth at which the potential density is 0.1kgm−3heavier than at the sea surface (10m). In the eastern sub- tropical North Pacific, where ESTMW is formed, a local MLD maximum exceeding 120m is observed in both model and observations. However, the center of the MLD, which is around (30˚N, 140˚W) in the observations (Fig.1a), appears to occur at (25˚N, 135˚W) in the model (Fig.1b). In agreement with the observations, the modeled outcropping isopycnals appear to range from 24.6σto 25.2σin the ESTMW formation region (the two thick black lines in Fig.1).

In this study, we define ESTMW as water in the region (20˚–35˚N, 150˚–120˚W) that satisfies the following con- ditions: it is a low-PV pycnostad with PV less than or equal to 210−10m−1s−1, a potential density between 24.6 and 25.2σ, and lying below the mixed layer. Here, the definition of PV is

whereis the Coriolis parameter,is the potential density, and0is the reference density (1024kgm−3). Fig.2 com- pares the core properties of ESTMW between the model and observations. OFES clearly does well in capturing the core temperature of 17–21.6℃ and core salinity of 34.5–35.3 in ESTMW. In both model (Fig.2d) and observations (Fig.2b), the core density of ESTMW appears to occur between 24.6 and 25.2σ, with a remarkable peak at 25.0σ.

Since our focus in this study is the effect of mesoscale eddies on ESTMW, validating the eddy properties in the formation region of the water is important. A first as- sessment of the modeled eddy activity compares the EKE and its variability with those in AVISO (Fig.3). Following Qiu(2014), EKE is defined by:

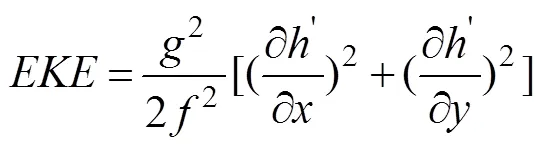
where g is the gravity constant, f is the Coriolis parameter, h'(x, y, t) is the SLA, and x and y are the zonal (positive eastward) and meridional (positive northward) coordi- nates, respectively. The modeled distribution pattern of annual mean EKE (Fig.3b) is quite similar to that in ac- tual observations (Fig.3a), and a relatively low EKE is found around the center of the ESTMW formation region. However, the model appears to overestimate the EKE over the region of Californian currents compared with those in observations. Fig.3c compares the time series of EKEs averaged over our region of interest. The modeled EKE appears to have seasonal and interannual variations similar to those in the observations, with linear correla- tion coefficients reaching 0.59 at the 99% confidence level. However, the modeled mean EKE level is higher than that in the observations. This difference may be due to the fact that the AVISO product only resolves the eddy signals with radii greater than 150 km (Qiu et al., 2014).

Fig.2 Occurrence frequency (%) of θ-salinity at the core of mode water from (a) ISAS15 and (c) OFES. Histogram fre- quency (%) of low PV with respect to core σθfrom (b) ISAS15 and (d) OFES. Maps of OFES and ISAS15 are calcu- lated over the region (20˚–35˚N, 150˚–120˚W) during April–June, while OFES is from 1994 to 2010 and ISAS is from 2002 to 2015, respectively.

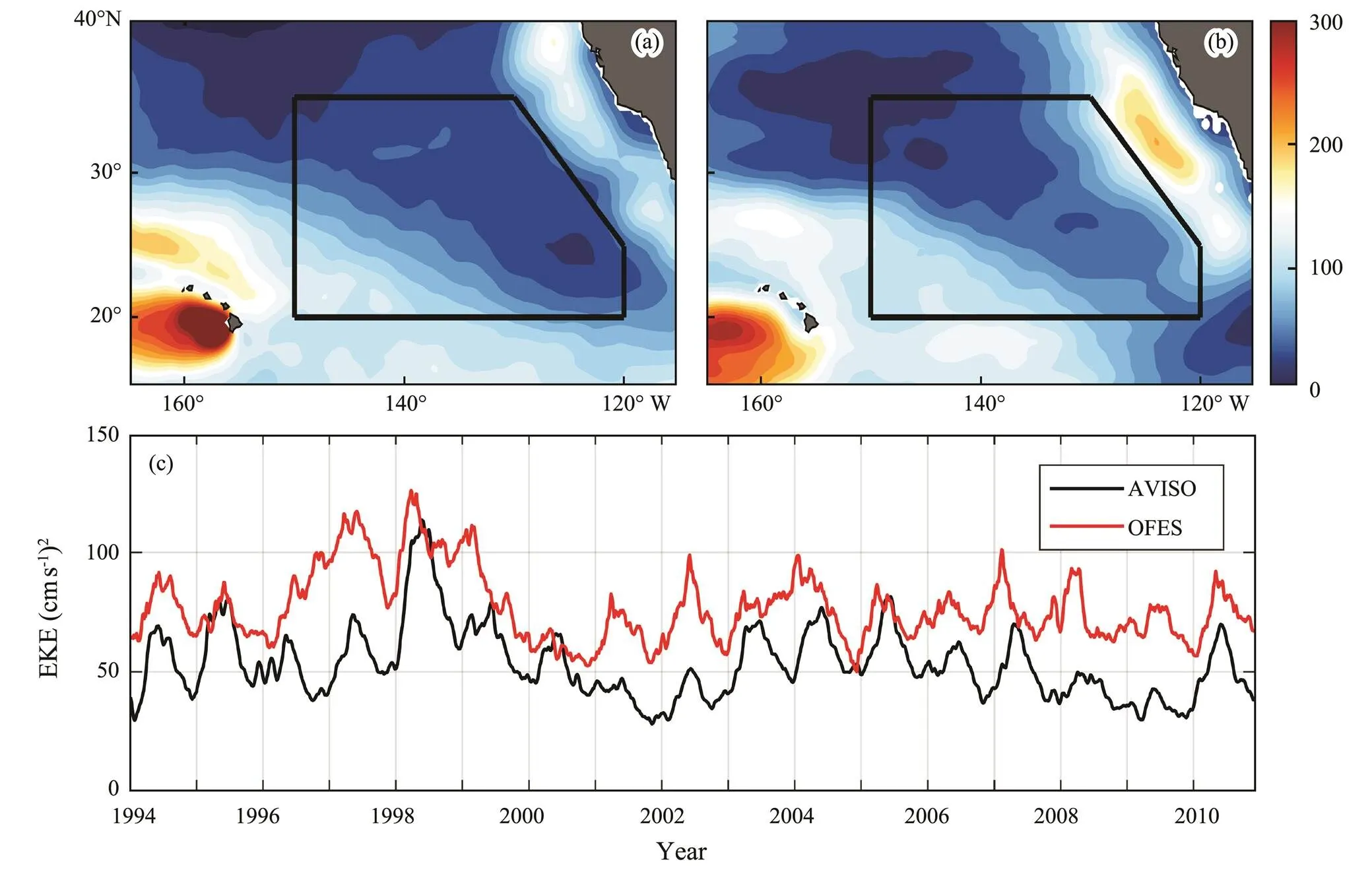
Fig.3 Annual mean surface EKEs calculated from the SLA of (a) AVISO and (b) OFES. (c) Time series of EKEs aver- aged over the black box in (a) and (b).

Table 1 compares the mean eddy properties over the region (20˚–35˚N, 150˚–120˚W) between AVISO and OFES. In the AVISO observations, the mean numbers of anticyclonic eddies (AEs) and cyclonic eddies (CEs) in a snapshot over the region during the period 1994–2010 are 30.8 and 31.1, respectively. The observed AEs and CEs have similar mean radii (about 80km) and amplitudes (about 3.5cm). The propagation velocities of AEs and CEs are –2.4 and –2.5cms−1in the zonal direction and –0.5 and –0.2cms−1in the meridional direction, respectively. Therefore, eddies in this region mainly propagate westward with a slight southward shift. The mean rotating geostrophic velocity calculated from the SSH anomaly is 6.7cms−1for both AEs and CEs. The ratio of eddy rotation velocity (U) to eddy propagation velocity (CandC) is much larger than 1, thus suggesting that the eddies are strongly nonlinear and can wrap water mass within their interior (Flierl, 1981; Chelton, 2011b).

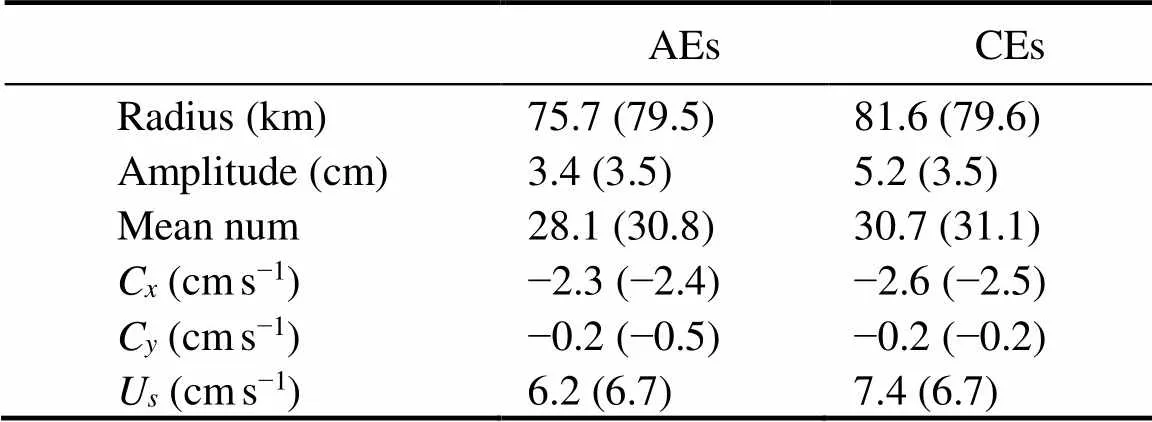
Table 1 Anticyclonic and cyclonic eddy properties inferred from OFES and AVISO (in brackets) in the region (20˚–35˚N, 150˚–120˚W)

Note: Only eddies with durations of over 15 days and amplitudes of over 1cm are considered.

In good agreement with the AVISO results, the modeled eddies exhibit similar statistical characteristics. However, while the modeled number of CEs is consistent with ob- servations, the model simulates fewer AEs compared with actual observations in this region. This result may be due to the filtering out of small structures; in this work, we focus on eddies with durations of over 15 days and am- plitudes of over 1cm in OFES, but AVISO smooths ADT fields and spreads out small eddies, thereby increasing their size (Chelton, 2011b).

Fig.4 shows the eddy radii and propagation velocities in AVISO and OFES over the region (20˚–35˚N, 150˚–120˚W). The shape similarity suggests that eddies in both model and observations have a consistent relationship be- tween the eddy radii and propagation velocities. In AVI- SO, the majority of eddies with radii ranging from 40km to 120km corresponds to a zonal propagation velocity of −6cms−1to 0cms−1and a meridional propagation veloc- ity of –4cms−1to 0cms−1. In OFES, the majority of ed- dies with radii ranging from 30km to 130km corresponds to a zonal propagation velocity of −6cms−1to 2cms−1and a meridional propagation velocity of −4cms−1to 2 cms−1.

Taking the results described above together, our favor- able model-observation comparisons suggest that the OF- ES output is reliable for examining the contribution of mesoscale eddies to the subduction and transport of EST- MW in the North Pacific.

Fig.4 Histogram frequency of eddy radii and (a, c) zonal and (b, d) meridional propagation speeds in (a, b) AVISO and (b, d) OFES. Only eddies with durations of over 15 days and amplitudes of over 1cm are considered.

4 Mean Fields

Fig.5 presents the evolution of PV, density, and MLD averaged over 140˚–130˚W in the longitudinal direction during March–June. In March, the mixed layer is as deep as about 110m, and the isopycnal surfaces ofσ<25.2kgm−3outcrop north of 25˚N. As the mixed layer shoals, the low-PV water pycnostad gradually loses contact with the atmosphere in April and is sheltered from the surface in May and June. This development indicates that the for-mation of ESTMW is due to shoaling of the deep winter mixed layer. The spatial distribution of PV and accelera- tion potential at 25.0σin June is shown in Fig.6a, which indicates that ESTMW forms in the eastern subtropical North Pacific and spreads southeastward (southwestward) to the north (south) of its formation region. Fig.6b shows the thickness of ESTMW, which is defined as the depth difference between the upper and lower ESTMW bounda- ries. The thickness of ESTMW is large over its formation region (20˚–35˚N, 150˚–120˚W); indeed, the maximum thickness exceeds 85m at around (25˚N, 137˚W).

Fig.5 Monthly climatological PV (color shaded, 10−10m−1s−1), σθ(black contours in 0.2kgm−3 intervals), and MLD (dashed black lines) averaged over 140˚–130˚W during March–June. The two thick black lines represent σθ=24.6kgm−3 and 25.2kgm−3 as indicated in the figures.

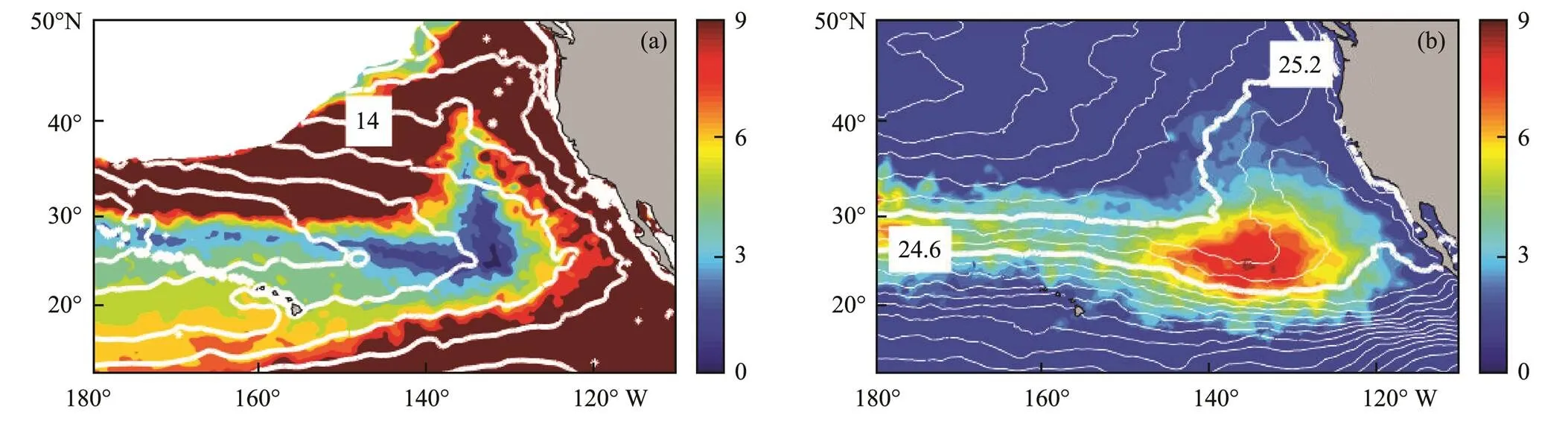
Fig.6 (a) Distribution of PVs (color shaded, 10−10m−1s−1)and acceleration potentials (white contours at 1.0m2s−2 inter- vals) at σθ=25.0 in June. (b) ESTMW thicknesses (color shaded, m) in June and mixed layer densities (white contours in 0.2kgm−3) in winter.

5 Contribution of Mesoscale Eddies to ESTMW

5.1 Subduction Rate

The subduction rate is used to examine the transport of low-PV water in the mixed layer to the main thermocline and may be calculated in Lagrangian or Eulerian coordi- nates (Qiu and Huang, 1995). According to previous stud- ies (Nishikawa, 2010; Liu, 2011; Xu, 2014; Liu, 2016), the Eulerian definition is a much better choice for diagnosing subduction in the eddy-re- solving model. In the Eulerian definition, the subduction rate can be written as:

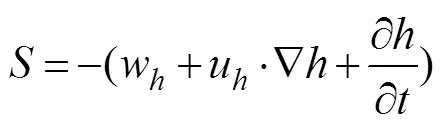
whereis the depth of the mixed layer,wanduare the vertical and horizontal velocities at the base of the mixed layer, respectively,u·Ñis the horizontal advection of fluid out of the mixed layer, and ∂/∂is the rate of mixed layer change. Adapted from Nishikawa(2010) and Xu(2014), the annual subduction of a density range (1≤<2) is given by:

where (,) is the horizontal grid index in the ESTMW formation region (20˚–35˚N, 120˚–150˚W), ΔA,jis the area of a grid box that falls within the surface density range,is the time, andis the averaging period. We obtain three subduction rates to evaluate the role of eddies on subduction in this region as follows: 1) total subductiontotalis obtained using the 3-day model output; 2) mean subductionmeanis obtained using monthly mean fields; and 3) eddy subductioneddyis the difference between the total and mean subductions (,eddytotal−mean).

Fig.7 showstotal,meanandeddyat 0.1σintervals. While both total and eddy subduction rates peak atσ=25.0 (Figs.7a and 7c), the peak of mean subduction rate appears at aroundσ=24.8–25.1 (Fig.7b). The total sub- duction of ESTMW is about 11.1Sv, with 7.7Sv contrib- uted by mean subduction and 3.4Sv contributed by eddy subduction. These results indicate that eddy subduction accounts for 31% of the total subduction of the ESTMW formation.

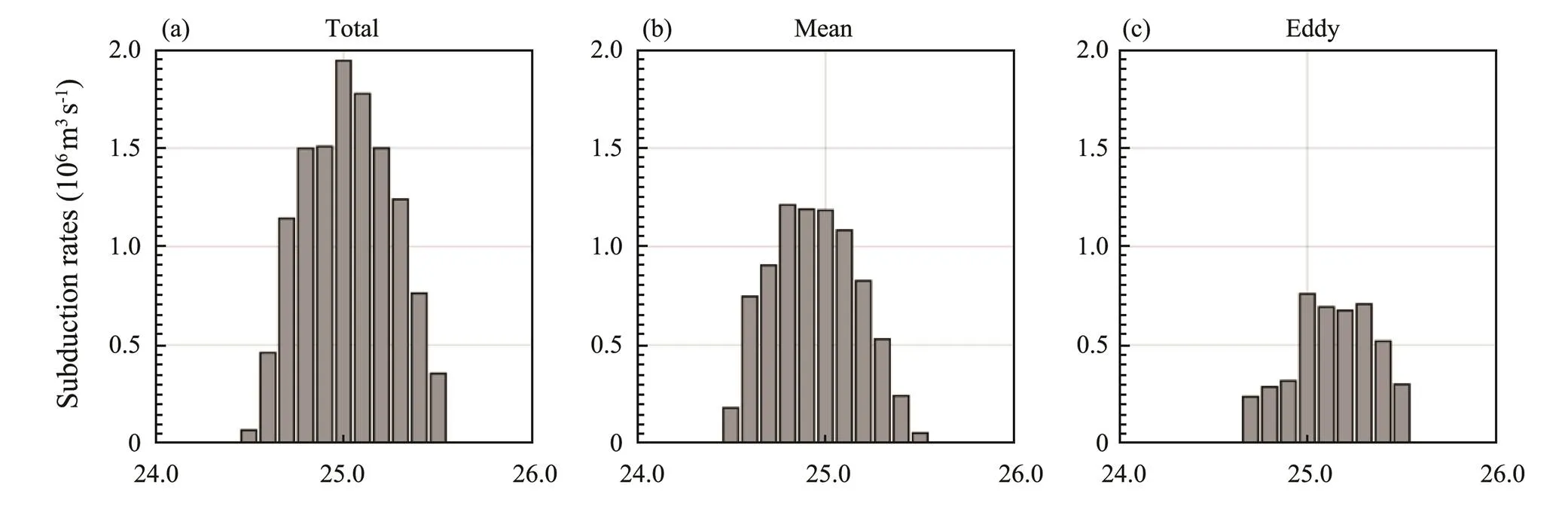
Fig.7 Three subduction rates (in 106m3s−1) of (a) Mtotal, (b) Mmean, and (c) Meddy at 0.1σθintervals over the region (20˚–35˚N, 120˚–150˚W).

5.2 Volume and Transport of ESTMW Trapped by Eddies

In this section, we estimate the volume and transport of ESTMW trapped by mesoscale eddies. PV, as a dynami- cally conserved quantity, has been widely used to identify an eddy’s ability to trap fluid, with regions of closed PV contours corresponding to the eddy wrapping material (Rhines and Young, 1982; Davey and Killworth, 1984; Early, 2011; Zhang, 2014). Eddies with no closed PV contour are considered to have no ability to trap ESTMW. In this study, we average low PVs (≤2×10−10 m−1s−1) between 24.6σand 25.2σbelow the mixed layer base and adopt the outermost closed PV contour as the subsurface material boundary in eddies. Thus, if the eddy core is wrapped by the closed PV contour, ESTMW is trapped in this eddy. The ESTMW volume within this eddy is integrated after identifying the lateral material boundary combined with the upper and lower ESTMW boundaries.

Our calculations reveal that the ESTMW volume in- creases after winter for both AEs and CEs (Fig.8a). The ESTMW volume does not peak during winter because of its great MLD. In May, when the connection of the sea with the air is cut off by the seasonal thermocline, the subsurface PV contours close more easily, and, thus, more ESTMW is trapped; the volume of ESTMW at this time is slightly greater in AEs than in CEs. The ESTMW volume trapped by all eddies in May reaches up to about 2.8×1013m3, which is approximately 16% of the total ESTMW volume of 1.7×1014m3(Fig.8b). After May, the ESTMW volume decreases gradually and reaches a minimum in December for both types of eddies. Fig.8b also shows that the model well captures the observed seasonal variations in total ESTMW volume, which peaks in May and reaches a minimum in December.

Fig.8 (a) Annual cycles of the ESTMW volume trapped by AEs (red line), CEs (green line), and all eddies (black line). (b) Annual cycles of the total ESTMW volume estimated by observations (red line) and the model (black line).

Fig.9 (a) Eddy-trapped and (c) total zonal ESTMW transport through meridional sections per degree of latitude (Sv/degree). Distribution of the meridionally integrated zonal transport trapped by (b) eddies (red line for AEs, green line for CEs, and black line for all eddies) and (d) total westward ESTMW transport in the area of 15˚–27˚N.

The distribution of eddy-trapped and total meridional ESTMW transport is displayed in Fig.10. The meridional transport trapped by eddies is mainly southward (Fig.10a). Similarly, we calculate the total meridional mean ESTMW transport and find southward movement because of the southward mean geostrophic velocity in this direction (Fig.6a). However, the eddy-trapped southward ESTMW transport (Fig.10b) only accounts for a small percentage of the total southward ESTMW transport (Fig.10d).

Fig.10 (a) Eddy-trapped and (c) total meridional ESTMW transport through zonal sections per degree of longitude (Sv/degree). Distribution of the zonally integrated meridional transport trapped by (b) eddies (red line for AEs, green line for CEs, and black line for all eddies) and (d) total ESTMW in the area of 150˚–120˚W.

6 Conclusions

This study investigated the characteristics of mesoscale eddies in the eastern subtropical North Pacific and their impact on the subduction and transport of ESTMW using the high-frequency output of an eddy-resolved OGCM. The main findings are as follows:

Comparison of the modeled eddies with actual obser- vations indicates that the model well captures eddy prop- erties, including eddy number, C, and Us. In addition, the ratio of Us to C is much larger than 1, thus suggesting that eddies in this region have strong nonlinearity and are able to trap water mass over long distances.

The total subduction of ESTMW is about 11.1Sv, with 7.7Sv contributed by mean subduction and 3.4Sv con- tributed by eddy subduction. Thus, eddy subduction ac- counts for 31% of the total subduction for ESTMW for- mation. Both total and eddy subduction rates of ESTMW peak atσ=25.0. The total ESTMW volume peaks at 1.7×1014m3in May, with 2.8×1013m3(16%) contributed by eddies. The ESTMW volume trapped by AEs is slightly larger than that trapped by CEs.

Total eddy-trapped ESTMW transport primarily occurs westward and is remarkable in the latitude band of 18˚–30˚N. Meridional integration over the region reveals that eddy-trapped westward ESTMW transport can reach ap- proximately 0.17Sv, which is approximately 18% of the total zonal ESTMW transport in the area, at 140˚W. There- fore, eddies are important for carrying ESTMW westward over the northeastern North Pacific Ocean.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 41676002). The OFES data were provided by the Asia Pacific Data Research Center (http:// apdrc.soest.hawaii.edu/dods/public_ofes/OfES/ncep_0.1_global_3day). The altimeter products were obtained from theCMEMS(http://marine.copernicus.eu/services-portfolio/ access-to-products/).

Bryden, H. L., and Brady, E. C., 1989. Eddy momentum and heat fluxes and their effects on the circulation of the equato- rial Pacific Ocean., 47 (1): 55-79.

Chelton, D. B., Gaube, P., Schlax, M. G., Schlax, M. G., Early, J. J., and Samelson, R. M., 2011a. The influence of nonlinear mesoscale eddies on near-surface oceanic chlorophyll., 334 (6054): 328-332.

Chelton, D. B., Schlax, M. G., and Samelson, R. M., 2011b. Global observations of nonlinear mesoscale eddies., 91 (2): 167-216.

Davey, M. K., and Killworth, P. D., 1984. Isolated waves and eddies in a shallow water model., 14 (6): 1047-1064.

Dong, C. M., McWilliams, J. C., Liu, Y., and Chen, D. K., 2014. Global heat and salt transports by eddy movement., 5: 1-6.

Early, J. J., Samelson, R. M., and Chelton, D. B., 2011. The evolution and propagation of quasigeostrophic ocean eddies., 41 (8): 1535-1555.

Faghmous, J. H., Frenger, I., Yao, Y. S., and Warmka, R., 2015. A daily global mesoscale ocean eddy dataset from satellite al- timetry., 2: 1-16.

Flierl, G. R., 1981. Particle motions in large-amplitude wave fields., 18: 39-74.

Gaillard, F., Autret, E., Thierry, V., and Galaup, P., 2009. Quality control of large argo datasets., 26 (2): 337-351.

Hautala, S., and Roemmich, D., 1998. Subtropical mode water in the northeast Pacific basin., 103 (C6): 13055-13066.

Hosoda, S., Xie, S. P., Takeuchi, K., and Nonaka, M., 2001. Eastern North Pacific Subtropical Mode Water in a general circulation model: Formation mechanism and salinity effects., 106 (C9): 19671-19681.

Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, J., Woollen, J., Zhu, Y., Leetmaa, A., Reynolds, R., Jenne, R., and Joseph, D., 1996. The NCEP/NCAR 40-year reanalysis project., 77 (3): 437-472.

Kolodziejczyk, N., Prigent-Mazella, A., and Fabienne, G., 2017. ISAS-15 temperature and salinity gridded fields.. https://doi.org/10.17882/52367.

Kolodziejczyk, N., Testor, P., Lazar, A., Echevin, V., Krahman, G., Chaigneau, A., Gourcuff, C., Wade, M., Faye, S., Estrade, P., Capet, X., Mortier, L., Brehmer, P., Schutte, F., and Kar- stensen, J., 2018. Subsurface fine-scale patterns in an anti- cyclonic eddy off cap-vert peninsula observed from glider measurements., 123: 1-18.

Kouketsu, S., Tomita, H., Oka, E., Hosoda, S., Kobayashi, T., and Sato, K., 2012. The role of meso-scale eddies in mixed layer deepening and mode water formation in the western North Pacific., 68: 63-77.

Liu, C., and Li, P. L., 2013. The impact of meso-scale eddies on the Subtropical Mode Water in the western North Pacific., 12 (2): 230-236.

Liu, L. L., Huang, R. X., and Wang, F., 2016. Subduction/ob- duction rate in the North Pacific diagnosed by an eddy-re- solving model., 34 (4): 835-846.

Liu, L. L., Wang, F., and Huang, R. X., 2011. Enhancement of subduction/obduction due to hurricane-induced mixed layer deepening., 58 (6): 658-667.

Luo, Y. Y., Liu, Q., and Rothstein, L. M., 2009. Simulated re- sponse of North Pacific Mode Waters to global warming., 36: L23609, DOI: 10.1029/2009GL0409.

Masumoto, Y., Sasaki, H., Kagimoto, T., Komori, N., Ishida, A., Sasai, Y., Miyama, T., Motoi, T., Mitsudera, H., Takahashi, K., Sakuma, H., and Yamagata, T., 2004. A fifty-year eddy-re- solving simulation of the world ocean: Preliminary outcomes of OFES (OGCM for the Earth Simulator)., 1: 35-56.

Masuzawa, J., 1969. Subtropical mode water., 16: 463-472.

McCartney, M., 1982. The subtropical recirculation of mode waters., 40: 427-464.

McCreary, J., and Lu, P., 1994. Interaction between the sub- tropical and equatorial ocean circulation: The subtropical cell., 24: 466-497.

McGillicuddy, D. J., Anderson, L. A., Bates, N. R., Bibby, T., Buesseler, K. O., Carlson, C. A., Davis, C. S., Ewart, C., Falkowski, P. G., Goldthwait, S. A., Hansell, D. A., Jenkins, W. J., Johnson, R., Kosnyrev, V. K., Ledwell, J. R., Li, Q. P., Siegel, D. A., and Steinberg, D. K., 2007. Eddy/wind interac- tions stimulate extraordinary mid-ocean plankton blooms., 316 (5827): 1021-1026.

Nakamura, H., 1996. A pycnostad on the bottom of the venti- lated portion in the central subtropical North Pacific: Its dis- tribution and formation., 52 (2): 171-188.

Nishikawa, S., Tsujino, H., Sakamoto, K., and Nakano, H., 2010. Effects of mesoscale eddies on subduction and distribution of subtropical mode water in an eddy-resolving OGCM of the western North Pacific., 40 (8): 1748-1765.

Pan, A. J., and Liu, Q., 2005. Mesoscale eddy effects on the wintertime vertical mixing in the formation region of the North Pacific Subtropical Mode Water., 50 (17): 1949-1956.

Qiu, B., and Huang, R. X., 1995. Ventilation of the North Atlan- tic and North Pacific: Subductionobduction., 25: 2374-2390.

Qiu, B., Chen, S. M., Klein, P., Sasaki, H., and Sasai, Y., 2014. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent., 44 (12): 3079-3098.

Qu, T. D., Xie, S. P., Mitsudera, H., and Ishida, K., 2002. Sub- duction of the North Pacific Mode Waters in a global high-resolution GCM*., 32 (3): 746-763.

Rhines, P. B., and Young, W. R., 1982. Homogenization of po- tential vorticity in planetary gyres., 122: 347-367.

Sasaki, H., Nonaka, M., Masumoto, Y., Sasai, Y., Uehara, H., and Sakuma, H., 2008. An eddy-resolving Hindcast simula- tion of the quasiglobal ocean from 1950 to 2003 on the earth simulator. In:. Hamilton, K., and Ohfuchi, W., eds., Springer, New York, 157-185.

Suga, T., Takei, Y., and Hanawa, K., 1997. Thermostad distribu- tion in the North Pacific subtropical gyre: The central mode water and the subtropical mode water., 27 (1): 140-152.

Sugimoto, S., and Hanawa, K., 2007. Further evidence for non-reemergence of winter SST anomalies in the North Pacific eastern subtropical mode water area., 63 (4): 625-635.

Talley, L. D., and Raymer, M. E., 1982. Eighteen degree water variability., 40: 757-775.

Toyama, K., Iwasaki, A., and Suga, T., 2015. Interannual varia- tion of annual subduction rate in the North Pacific estimated from a gridded argo product., 45 (9): 2276-2293.

Toyoda, T., Awaji, T., and Ishikawa, Y., 2004. Preconditioning of winter mixed layer in the formation of North Pacific east- ern subtropical mode water., 31 (17): 1-5.

Toyoda, T., Awaji, T., Masuda, S., Suguura, N., Igarashi, H., Mochizuki, T., and Ishikawa, Y., 2011. Interannual variability of North Pacific eastern subtropical mode water formation in the 1990s derived from a 4-dimensional variational ocean data assimilation experiment., 51 (1-2): 1-25.

Toyoda, T., Fujii, Y., Kuragano, T., Kosugi, N., Sasano, D., Kamachi, M., Ishikawa, Y., Masuda, S., Sato, K., Awaji, T., Hernandez, F., Ferry, N., Guinehut, S., Martin, M., Peterson, K. A., Good, S. A., Valdivieso, M., Haines, K., Storto, A., Masina, S., Kohl, A., Yin, Y., Alves, O., Smith, G., Chang, Y. S., Vernieres, G., Wang, X. C., Forget, G., Heimbach, P., Wang, O., Fukumori, I., Lee, T., Zuo, H., and Balmaseda, M., 2017. Interannual-decadal variability of wintertime mixed layer depths in the North Pacific detected by an ensemble of ocean syntheses., 49 (3): 891-907.

Uehara, H., Suga, T., Hanawa, K., and Shikama, N., 2003. A role of eddies in formation and transport of North Pacific Subtropical Mode Water., 30 (13): 1705.

Xie, S. P., Kunitani, T., Kubokawa, A., and Kubokawa, A., 2000. Interdecadal thermocline variability in the North Pacific for 1958–1997: A GCM simulation., 30: 2798-2813.

Xu, L. X., Li, P. L., Xie, S. P., Liu, Q., Liu, C., and Gao, W. D., 2016. Observing mesoscale eddy effects on mode-water sub- duction and transport in the North Pacific., 7: 1-9.

Xu, L. X., Xie, S. P., McClean, J. L., Liu, Q., and Sasaki, H., 2014. Mesoscale eddy effects on the subduction of North Pa- cific Mode Waters., 119 (8): 4867-4886.

Zhang, Z. G., Wang, W., and Qiu, B., 2014. Oceanic mass trans- port by mesoscale eddies., 345 (6194): 322-324.

April 16, 2019;

May 23, 2019;

June 3, 2019

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2019

. Tel: 0086-532-66782796

E-mail: yiyongluo@ouc.edu.cn

(Edited by Xie Jun)