System Reliability Analysis of an Offshore Jacket Platform

ZHAO Yuliang, DONG Sheng, *, JIANG Fengyuan, and GUEDES SOARES Carlos

System Reliability Analysis of an Offshore Jacket Platform

ZHAO Yuliang1), DONG Sheng1), *, JIANG Fengyuan1), and GUEDES SOARES Carlos2)

1) College of Engineering, Ocean University of China, Qingdao 266100, China 2) Centre for Marine Technology and Ocean Engineering (CENTEC), Instituto Superior Técnico, Lisboa 1049-001, Portugal

This study investigates strategies for solving the system reliability of large three-dimensional jacket structures. These structural systems normally fail as a result of a series of different components failures. The failure characteristics are investigated under various environmental conditions and direction combinations. The-unzipping technique is adopted to determine critical failure components, and the entire system is simplified as a series-parallel system to approximately evaluate the structural system reliability. However, this approach needs excessive computational effort for searching failure components and failure paths. Based on a trained artificial neural network (ANN), which can be used to approximate the implicit limit-state function of a complicated structure, a new alternative procedure is proposed to improve the efficiency of the system reliability analysis method. The failure probability is calculated through Monte Carlo simulation (MCS) with Latin hypercube sampling (LHS). The features and applicability of the above procedure are discussed and compared using an example jacket platform located in Chengdao Oilfield, Bohai Sea, China. This study provides a reference for the evaluation of the system reliability of jacket structures.

system reliability; jacket platform;-unzipping technique; artificial neural network; latin hypercube sampling; response surface

1 Introduction

Jacket platforms play a vital role in offshore oil and gas development, and thus, it is very important to evaluate their system reliability. The system reliability theory of complicated structures usually has two meanings: First, the system is a combination of structural components, which have certain functional relationships. Second, there is a clear evolution of components failure, leading to progressive changes in the topological structure of the system undergoing failure. However, the redistribution of structural stress and strain increases the difficulty in identifying and analyzing structural failure modes. For large statically indeterminate marine structures, the failure of a single element usually does not lead to the failure of the entire structural system. After a single element fails, the internal forces will be redistributed among the remaining elements, which will still be able to withstand the redistributed internal forces. This implies that the statically indeterminate structure will fail only when several component failures occur.

The system reliability analysis of large and complex structures generally includes the following steps (Murotsu., 1984; Feng, 1988): building an uncertainty model of load and resistance variables, determining the limit-state function of a failed component, and finding the primary failure paths of the structure, and finally using a simplified model to predict the failure probability of the structural system. Since the 1980s, scholars from various countries have conducted numerous studies on the reliability analysis of structural systems and proposed many approaches to identify the main failure modes of structural systems, such as the branch-and-bound method and the-unzippingmethod (Thoft-Christensen and Murotsu, 1986; White and Ayyub, 2010). In general, the failure of the structural system is divided into some subsequences. Gholizad. (2012) divided a special fatigue failure scenario into a finite number of sub-scenarios, and the failure probability of the entire system is calculated by solving all combined sequences. Some studies have shown that the branch-and-bound technique is an effective approach to determine main failure scenarios. Shabakhty (2011) identified the important sequences leading to the platform collapse, and the system reliability was obtained through a combination of important failure paths. Kurian. (2014) established the main failure paths using the branch-and-bound technique and determined the structural reliability of an existing platform in Malaysia. Moreover, some other techniques have also been proposed to search for critical failure paths. Chen. (1996) applied an artificial intel-ligence-based technique to perform a reliability analysis of a space frame structure, but they still could not identify all the mechanisms compared with the-unzipping method. To generate failure modes more intelligently, Shao and Murotsu (1999) proposed a new selective search procedure combined with a genetic algorithm; the method overcomes the shortcoming of important failure modes being ignored. Feng (1988) improved Moses’ criterion of maximum load-bearing ratio and proposed an optimization criterion method for the main failure modes of structural systems. Thoft-Christensen (1990) introduced a modification of the procedure used in the-unzipping method for the identification of critical failure modes, and the modified failure tree is based on risks rather than the probabilities of failure. Gharaibeh(2002) presented a reliability-based methodology to identify and rank important members in structural systems under different material behaviors and different stiffness sharing factors and developed a rational methodology for the prediction of critical members in structural systems. Some other approaches based on variable distribution for the reliability analysis of jacket platform have been proposed considering extreme environments (Gholizad., 2012; Hezarjaribi, 2013).

To assess the reliability of large statically indeterminate structures, a number of numerical simulations are often needed, and this takes a lot of computational effort. Some scholars (Elhewy., 2006) have found that the artificial neural network (ANN) model, which is trained with relatively few results obtained by finite element analysis, can accurately and conveniently predict the relationship between structural response and input variables. Cho (2009) determined the limit-state function of slopes by using an ANN-based response surface to reduce the number of numerical calculations. Chojaczyk. (2015) presented a survey on the development of an ANN model in the reliability analysis of steel structures; the survey showed that for complex structures, the ANN-based reliability analysis methodologies are efficient alternatives compared with traditional reliability analysis methods. Vazirizade. (2017) trained an ANN using Monte Carlo simulation (MCS) and evaluated the seismic reliability of proposed structures. The training set selection techniques are very important for neural network-based methods of solving structural reliability (Chojaczyk., 2015). Latin hypercube sampling (LHS) has been widely adopted to generate samples for regression analysis and construct the response surface (Gaspar and Guedes Soares, 2013; Kang., 2015). Monte Carlo method and response surface approaches have also been widely used in structural reliability analysis (Gaspar., 2015; Pan and Dias, 2017; Sadoughi., 2018).

In recent years, some scholars (Bai., 2016; Asgarian., 2019) have studied the pile-soil interaction and reliability evaluation of jacket platforms. However, the present work studies the system reliability analysis of a jacket platform. Here the main paths that may lead to the failure of the entire system are found based on the-unzipping technique, and the structure is simplified to a simple series-parallel system (see Fig.1). Existing formulas such as the Ditlevsen bounding formulas can be used to approximately calculate the structural system reliability. In addition, the limit-state function of the complex structure is determined by obtaining the response surface basedon the ANN method. The random input variables are produced by the LHS method, and the failure probability can be estimated through MCS.

The first step is to determine the primary failure components in each failure path, which can be performed by obtaining the reliability index () of every component of the jacket platform. Then, it is necessary to calculate the reliability index of the remaining components after the first main failure component is generated and the strain and stress of the structure are redistributed. A failure path is composed of a finite number of critical failure components. Finally, the failure probability of the entire structure can be determined by solving combinations of all failure paths. Considering that components with a small reliability index are more vulnerable to failure, more detailed information on the failure behavior of the whole system are provided. Using this method, critical failure paths can be found, and weak members of a jacket platform can be reinforced.

Fig.1 Simplification of structural system failure.

For more convenient and quick access to jacket system reliability, a method using response surface based on the ANN method is proposed. In this study, these two methods are used to analyze the system reliability of a jacket platform located in Chengdao Oilfield, Bohai Sea, China (see Fig.2). These methods can be used to evaluate the reliability of jacket platforms under different service conditions.

Fig.2 Map of Chengdao Oilfield in theBohai Sea.

The methodology of system reliability assessment is presented in Section 2. An ANN model is created to replace the response surface of the structure and determine the limit-state function introduced in Section 3. A practical numerical example of a jacket platform located in Chengdao Oilfield, Bohai Sea is presented in Section 4. Using the established model, Section 5 discusses the system reliability analysis for the selected offshore jacket platform. Finally, the conclusions are summarized in Section 6.

2 System Model Simplification

Since the failure of one single component will not lead to the entire structure failure, the-unzipping approach confirms the main failure components of each failure path by comparing the magnitude of the reliability index. The-unzipping technique is used to calculate the reliability index () of a single component during the structural system failure process to determine the critical failure components that form different failure paths. The component with the minimum reliability index is chosen as the first failure component; then, the structure is modified and the stress is redistributed; the reliability index values of the remaining components are recalculated, and the component with the minimum reliability index is selected as the second failure component; the structure modification, and calculation are repeated until the structural system fails to serve its original purpose. Finally, these critical failure components form one failure path, which can be simplified as a parallel system, and all the failure paths are com- posed of a series system. Thus, the entire structural system is simplified as a series-parallel system, which makes performing reliability analysis easy.

2.1 Reliability Prediction of Single Component

Assume that a set of random variables related to structural reliability analysis is=[12···X]; then, a limit-state function=() can be established to describe the relationship between structural safety and thosebasic random variables. In this approach the safety margin of the structure for judging whether the structure fails or not can be expressed by defining functional relations between strength () and load () parameters as follows:

whereRdenotes random variables describing the strength of structural components;Srepresents the load effect applied on the structure, and it can be defined as

wherePis the external load acting on the structure, andadenotes the load factor, which can be calculated by finite element analysis.

Cornell (1969) deduced the formula of the reliability indexwith the normal distribution ofand:

whereandare the mean and standard deviation of, respectively.

The components with smaller reliability index values are selected as the critical components to start failure, which means that only the failed component whose reliability index is in the interval [β,β+Δβ] (β=minβ, Δβis a given positive number) is considered. The next step is to calculate the reliability index values of the remaining components to determine other failure components of a certain failure path.

2.2 Reliability Index Calculation of Remaining Components

Each failure path consists of multiple failed components. In this section, it is intended to find the next failure member after one is generated. This requires a new finite element analysis of the structure. The first failed component is removed, and the components of marine structures are generally ductile. The first failed component still has resistance ability after failure. Therefore, the first failed component is removed from the structure, and a pair of ‘additional loads’ are applied on the structure to represent the residual resistance. The loads can be given by

whereRrepresents the resistance of the failed component, andγis the coefficient of resistance, 0<γ<1. Then, the load effect of the remaining components can be written as

where,bandαdenote the influence factors of the concentrated loadPand additional loadF, respectively. Herein, the reliability index of the remaining component is given by

The next failure component can also be selected according to the method in Section 2.2. The steps in Sections 2.1 and 2.2 are repeated to determine the critical failure paths and the corresponding failure components composition.

In this study, four failure components can be identified using the above method for each failure path to meet the corresponding accuracy requirements. The elements in each failure path form a parallel system. A failure system with multiple failure paths can be simplified to a series system consisting of a number of parallel systems, and then, the structural system reliability can be estimated.

2.3 System Reliability Calculation

As previously mentioned, the failure path is a parallel system composed of failed components, and failed components in the same failure path have a certain correlation. The failure probability is given by

The failure path of the structural system constitutes a series system, and the failure probability of a series system can be obtained by the calculation method proposed by Ditlevsen (1979):

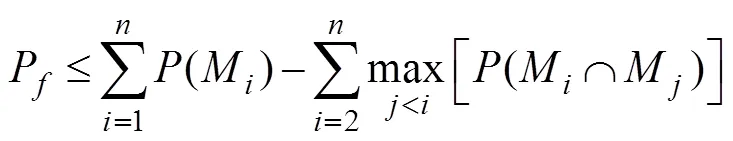
whereMstands for the failure event caused by failure paths.

3 ANN-Based Response Surface Method

As previously mentioned, sophisticated numerical me- thods will spend too much computational effort when reliability analysis is applied to a complicated structural system (Elhewy, 2006). The efficiency of reliability analysis can be improved by selecting the data from finite element method (FEM) and training the ANN to define the relationship between input variables and structural response. The difference between the ANN method and general polynomial fitting is that the relationship between structural response and environment variables is implicit and there is no definite expression form. It is confirmed that neural network prediction is more effective and accurate than polynomial fitting when the functional relationship between structural response and input variables is unclear (Elhewy, 2006).

Fig.3 shows the procedure of the ANN-based response surface method. As can be seen in the picture, there are two main steps to solve the probability of failure. First, random environmental variables from a certain distribution are produced using the LHS method. The response of a structure is obtained by finite element analysis, and the results together with input variables are used to train an ANN. Second, an ANN model is created to replace the response surface of the structure and determine the limit-state function. The failure probability can be estimated with a large number of variable samples produced by LHS through MCS.

3.1 RBF Neural Network Model Establishment

Artificial neural network is a network system composed of a large number of simple forms of interconnected neurons. It can simulate nonlinear and implicit functions based on the neural structure of the brain (Deng, 2005). A radial basis function (RBF) neural network is a three-layer neural network that includes an input layer, hidden layer, and output layer. The transformation function of the hidden layer is a Gaussian function of the local response. The structure of the RBF neural network in this work is shown in Fig.4.

In this neural network, the transfer function is the distance between the weight vector and the threshold vector as an argument; therefore, the input of theth neuron of the hidden layer is obtained as

The output is

where1represents the weight vector of each neuron of the hidden layer connected to the input layer;denotes the input variables;1is the threshold.

The output of the output layer is the weighted summation of the output of the neurons in each hidden layer. Because the excitation function is a purely linear function, the output is

When a jacket structure is determined, the structural response has a strong correspondence with environmental load parameters.

wheres,p,w,c, andirepresent wave significant height, peak period, wind speed, current velocity, and ice thickness, respectively;() is the response of the jacket structure that cannot be well represented with explicit expressions.

Fig.3 The procedure of the proposed ANN-based approach.

Fig.4 The structure of RBF neural network.

3.2 Reliability Assessment Combining ANN Model

Once the RBF neural network is trained and validated, it will be used to describe the limit function of the jacket structure as the response surface can be defined by the RBF neural network model (Rackwitz and Fiessler, 1978)

Then, MCS combined with the ANN model is successfully applied in this study for system reliability analysis:

The main steps of this procedure are as follows: 1) A series of environmental variable parameters are randomly generated, and in this process, LHS is adopted to generate values for all random variables that follow a certain distribution type. 2) The random variables are provided for the limit-state function. 3) The calculation is repeated until the stop criterion is satisfied.

4 Numerical Example

In this section, an example jacket located in Chengdao Oilfield, Bohai Sea, is analyzed using both the-unzipping approach and ANN-based approach. The jacket plan dimensions are 12.28m×12.28m at mud line elevation, and the slope is 1:10. The jacket platform work elevation is 12.0m, mud line elevation is −15.8m, and static water level elevation is 0.0m. The superstructure of this platform refers to an old mono-pile platform that is simplified to a plane with a height of 20m and a width of 10m. A general configuration of a modeled jacket structure using ANSYS software is displayed in Fig.5, and the main components sizes are listed in Table 1. In general, the effect of uncertainties in components sizes caused by corrosion or other factors is considered in reliability the analysis of the jacket platform. This is particularly important for old structures whose sizes may have changed. However, this jacket is categorized as a newly installed platform for which there is no initial imperfection. Thus, the uncer-tainties of structural parameters are not considered in this study. The structural system reliability of the jacket platform under extreme sea states is calculated using the two considered approaches. In winter, the Bohai Sea exhibits a freezing phenomenon due to the frequent invasion of the strong cold wave. Thus, the design conditions and reliability analysis consider combinations of wind, current, and wave or ice in different seasons. The environmental parameters are represented in Section 5. Moreover, the direction combinations of environmental loads are considered in the numerical simulation.

Fig.5 Finite element model of jacket platform.

Table 1 Sizes of jacket platform main components

4.1 Jacket Pile Foundation

A part of the environmental load acting on the jacket will be converted into pile-soil interaction. In this study, the soil is composed of seven layers and the parameters are shown as Fig.6. The interaction between pile and soil is simulated by a soil spring using the so-called-curves (Dong and Sang, 2014), as illustrated in Fig.7. The Association of Petroleum Industry (API) Recommended Practice 2A criteria suggest how to make a clay spring as follows:

wherepdenotes the standard value of the ultimate strength of the ground soil underdepth per unit area of pile side;Canddenote the undrained shear strength and bulk density of the ground soil, respectively;is the foundation diameter;zis the depth of the turning point of the ground soil ultimate strength; andis the arbitrary depth of foundation below the mud surface.

whereis the horizontal soil resistance, andis the lateral horizontal displacement of the foundation;50is the lateral displacement of the foundation at half of its ultimate strength of the ground soil.

The API suggests how to make sandy soil as follows:

whereCrepresents coefficients from API codes.

whereis the initial modulus of subgrade reaction, and it is related to the internal friction angle of soil;is the lateral displacement; andis a resistance coefficient, defined in Eq. (22).

Fig.6 Soil properties.

Fig.7 p-y curves at depth z below mud surface.

4.2 Environmental Load Calculation

4.2.1Ice load

Under the action of wind and current, the extremal ice force generated by the squeezed pile of a large-area ice canbecalculatedasfollows(ClassificationSocietyofChina (CCS), 2003; API-RP-2N, 2015):

whererepresents the shape factor of the pile (=0.9 for a cylindrical object);1and2are the local extrusion coefficient and contact coefficient, respectively;Rrepresents the ultimate compressive strength of the ice specimen;the width of the pile; andthe ice thickness.

4.2.2Wind load

The wind load acting on the offshore platform can be calculated as follows (API-RP-2A, 2007):

whereis wind pressure on the projected area;ρis the mass density of air;CandCare height and shape coefficients, respectively, which are described in API guidelines;denotes the projected area perpendicular to the wind direction;is the wind speed. A wind velocity at a height 10m above the mean water level is adopted in this study.

4.2.3Wave load

The API suggests that when the ratio of the wavelength to the member diameter is large (>5), Morison formula should be adopted to calculate wave loads on a cylindrical object:

whereuis the horizontal velocity of the water particle at arbitrary heightof the cylinder;is the diameter of the component;is seawater density;CandCare the drag and additional mass coefficient, respectively.

The API shows the applicability regions of Stokes V and various orders of stream function solution in the dimensionless wave steepness, and the dimensionless relative depth plane. According to the wave height, wave period, and water depth, Stokes’ fifth-order wave theory is chosen to calculate the velocity and acceleration of water particles; then, the wave loads are computed.

4.3.4Current load

The current loads acting on a fixed slender structure can be calculated as follows (CCS, 2003):

whereis current velocity; there is a linear current profile in this calculation, in which the current velocity is maximum in the sea surface and is minimum in the sea bottom, as depicted in Fig.8;is the current coefficient; the other parameters are the same as in the wave load formula.

Fig.8 Schematic depiction of environmental loads.

5 Analysis and Results

5.1 Load Application

To define the reliability index of each component, determining the load influence factors is necessary; therefore, the environmental loads are converted into equivalent concentrated forces acting on the jacket joints, which are numbered as depicted in Fig.9. The international code ISO/CD 19906 (2007) gives a description of the Bohai Sea technique information including climatology and hydrology. Wind speeds during the winter months are between 5ms−1and 7ms−1with maximum speeds in the range of 35ms−1to 40ms−1; the currents are usually less than 1ms−1but can reach 2ms−1; wave heights are most severe in winter, and the maximum wave height is in the 3.5m to 6.0m range; the wave parameters are conservative in this calculation. CCS (2003) suggests that when the measured data are insufficient, the ice thickness of the Bohai Sea should be 0.8m. The environmental loads are classified into ice and ice-free conditions, whose parameters are presented in Table 2. Three direction combinations of environmental loads are considered in the numerical calculation: i) all environmental loads are along the-axis; ii) current load and ice load are along the-axis, while the angle between the-axis and the wind load is 45˚; iii) current load and ice load are along the-axis, while the angle between the-axis and the wind load is 90˚.

Table 2 Environmental load parameters and acting position

Fig.9 Schematic depiction of node and component number.

5.2 Latin Hypercube Sampling for Environmental Variables

Latin hypercube sampling is a kind of stratified sampling technique. Here, the cumulative distribution curve of variables is divided into equal intervals on the scale (0, 1) and then samples are taken from each interval or layer of the probability distribution. In this work, the parameters of wind, wave, and current are assumed to be normally distributed, and the ice parameters are in accordance with the logarithmic normal distribution, as displayed in Table 3. Sampling examples of 100 points obtained by the LHS method are illustrated in Fig.10. It can be seen that the sampling points follow the specified dis- tribution and are uniformly distributed within the cumulative probability range.

Table 3 Stochastic models for environmental variables

Notes:vdenotes wind speed;vdenotes current speed;Hdenotes significant wave height;Tdenotes wave period;tdenotes ice thickness.

5.3 ANN Model Establishment

An ANN is a nonlinear, adaptive information processing system composed of a large number of processing units. There are three major steps to establish an ANN model (Elhewy., 2006): First, the structure of the model is determined; second, the model is trained with a set of training data; lastly, the ANN model is validated and tested with the remaining data.

In this work, 70% of the full database generated by FEM is employed for training (70), and 30% is reserved for testing (30). The training process will stop if the validation error does not keep decreasing. The test results are displayed in Fig.11 and Fig.12; they show a good agreement with the results obtained by FEM. The trained ANN model is used to approximate the limit-state function of the jacket structure so that the number of finite element analysis is reduced and computational efficiency is significantly increased.

5.4 Results and Discussion

5.4.1-unzipping method with different environmental loads

The strength of each component is assumed to be normally distributed. The coefficient of variation (COV) of yield stress is taken as 0.1, and the COV of each load is 0.3. The tensile strength of this steel structure isσ=315MPa. Under working conditions, the allowable stress is []=189MPa, and the allowable stress can increase by one third under extreme environmental conditions. The critical failure paths and failure probability of the structural system with different environmental loads are presented in Tables 4 and 5. The results considering direction combinations are presented in Tables 4, 6, and 7. One critical failure path is depicted in Fig.13.

Fig.10 Sampling points generated by the LHS method.

Fig.11 Comparison of results from ANN and FEM.

Fig.12 Prediction mean error with network correction.

Table 4 Failure paths and system failure probability under wind-ice-current condition

Table 5 Failure paths and system failure probability under wind-wave-current condition

Table 6 Failure paths when the angle between the wind load and the current and ice loads is 45˚

Table 7 Failure paths when the angle between the wind load and the current and ice loads is 90˚

5.4.2 ANN-based method

The structural response with different environmental variables can be predicted by the RBF neural network, and then, the limit-state function of the structure is defined as Eq. (28) using the allowable maximum displacement at the top of the jacket platform:

whereallis the maximum allowable displacement of the structure, andstis the static response of the structure.

The failure probability of the structural system is estimated by 107times MCS with LHS.

P=4.5×10−6.

5.4.3 Discussion

In the first phase of this study, the-unzipping technique is adopted to assess the structural system reliability of a jacket structure under different environmental loads combinations such as wind, current, wave or ice loads. In this method, the reliabilities of different components in the structure are evaluated, and the-unzipping technique is used to determine the critical failure paths of the structure, as shown in Tables 4–7. Based on the results, the diagonal bracings are confirmed to be weak components and thus should be paid additional attention for structural monitoring and protection. Moreover, as the main control load, the reliability index of the jacket structure under ice loads is several orders of magnitude lower than that in the condition of no ice.

Fig.13 The component composition of a certain failure path.

In the second phase, the reliability of the entire system is evaluated considering the direction combinations of environmental loads. When the direction of wind loads is different from those of current and ice loads, the failure paths are found to be similar; this is because the-unzipping technique confirms that the diagonal bracings are weak components of the jacket structure; if one diagonal brace fails, the stress redistribution will cause the other adjacent members to fail; therefore, the failure paths are mostly composed of weak diagonal bracings. While different directions of environmental loads will lead to different orders of failure paths and reliability results. The load effect coefficient of a member is the largest under the same direction of environmental loads, which leads to the lowest reliability index of the structure.

In the third phase, an approximate method combining the ANN model with MCS is proposed to calculate the structural reliability of the jacket structure to reduce the calculation cost. An RBF neural network is adopted to fit the limit-state function, which cannot be expressed by an explicit formula. The results show that this approach has an acceptable accuracy compared with the-unzipping technique and has a high computational efficiency.

Based on the results, the accuracy and advantages of these two approaches for structural reliability assessment of a jacket structure are validated and discussed. Using the-unzipping technique, detailed information of the failure behavior of different components can be provided and the critical failure paths of the entire structure can be determined, which can provide a reference to reinforce the corresponding weak components. For complicated marine structures, the ANN model combined with MCS can be used to calculate structural reliability with an acceptable accuracy and lower computational cost. These two approaches can be used to calculate the system reliability of existing offshore structures. For marine structures, the component inspection and reinforcement can be performed using the-unzipping technique while considering their in-service condition.

6 Conclusions

The-unzipping technique and the ANN-based method are individually used to analyze the system reliability of a jacket platform in Chengdao Oilfield, Bohai Sea. Considering the soil-pile interaction, the system reliability of the jacket platform is=4.79 under wind-ice-current conditions, and the reliability assessment results show that the failure probability of the structure with ice load is several orders of magnitude higher than that without ice. Hence, the ice load is the main load acting on the jacket platform. Therefore, the reliability of jacket offshore platform can be checked directly under wind-ice-current conditions in icy-sea areas.

In the process of determining the main failure path of the system, the failure probability of the inclined brace of the jacket is found to be higher than those of other components. It can be determined that the inclined brace that is most likely to fail first is on the plane that is parallel to the wave direction. When the first inclined brace fails, the connected brace has a high probability of failure after the stress redistribution. The stress distribution will affect the related part of the transverse bracing structure.

It can be seen from the analysis of examples that the-unzipping technique is relatively rigorous and can directly obtain the failure paths of a structural system. However, when the structural system model can be established accurately and the limit-state function of the structural system can be defined correctly, the ANN-based response surface method can be used to calculate the system reliability conveniently and quickly, especially for a more complicated structure, which can dramatically reduce computational efforts.

Acknowledgements

The study was supported by the National Natural ScienceFoundationofChina(No.51779236),theNSFC-Shan-dong Joint Fund Project (No. U1706226), and the National Key Research and Development Program (No. 2016YFC0303401).

API RP 2A, 2007.. American Petroleum Institute, Washington, D. C., 60-63.

API RP 2N, 2015.. American Petroleum Institute, Washington, D. C., 16-17.

Asgarian, B., Zarrin, M., and Sabzeghabaian, M., 2019. Effect of foundation behaviour on steel jacket offshore platform failure modes under wave loading., 14 (6): 570-581.

Bai, Y., Yan, H., Cao, Y., Kim, Y., Yang, Y., and Jiang, H., 2016. Time-dependent reliability assessment of offshore jacket platforms., 11 (6): 591-602.

CCS, 2003.. Classification Society of China, 13-15 (in Chinese).

Chen, K. S., Zhang, S. K., and Huang, W., 1996. Artificial intelligence-unzipping method in structural system reliability analysis., 60 (4): 619-626.

Cho, S. E., 2009. Probabilistic stability analyses of slopes using the ANN-based response surface., 36 (5): 787-797.

Chojaczyk, A. A., Teixeira, A. P., Neves, L. C., Cardoso, J. B., and Guedes Soares, C., 2015. Review and application of Artificial Neural Networks models in reliability analysis of steel structures., 52 (3): 78-89.

Cornell, C. A., 1969. A probability-based structural code., 66 (12): 974-985.

Deng, J., Gu, D., Li, X., and Yue, Z., 2005. Structural reliability analysis for implicit performance functions using artificial neural network., 27: 25-48.

Ditlevsen, O., 1979. Generalized second moment reliability index., 7 (4): 435-451.

Dong, H. K., and Sang, G. L., 2014. Reliability analysis of offshore wind turbine support structures under extreme ocean environmental loads., 79 (1): 161-166.

Elhewy, A. H., Mesbahi, E., and Pu, Y., 2006. Reliability analysis of structure using neural network method., 21 (1): 44-53.

Feng, Y. S., 1988. Enumerating significant failure modes of a structural system by using criterion methods., 30 (5): 1152-1157.

Gaspar, B., and Guedes Soares, C., 2013. Hull girder reliability using a Monte Carlo based simulation method., 31 (31): 65-75.

Gaspar, B., Bucher, C., and Guedes Soares, C., 2015. Reliability analysis of plate elements under uniaxial compression using an adaptive response surface., 10 (2): 145-161.

Gharaibeh, E. S., Dan, M. F., and Onoufriou, T., 2002. Reliability-based importance assessment of structural members with applications to complex structures., 80 (12): 1113-1131.

Gholizad, A., Golafshani, A. A., and Akrami, V., 2012. Structural reliability of offshore platforms considering fatigue damage and different failure scenarios., 46 (2): 1-8.

Hezarjaribi, M., Bahaari, M. R., Bagheri, V., and Ebrahimian, H., 2013. Sensitivity analysis of jacket-type offshore platforms under extreme waves.,83 (2): 147-155.

ISO/CD 19906, 2007.International Organization for Standardization, 338-340.

Kang, F., Han, S. X., Salgado, R., and Li, J. J., 2015. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling., 63: 13-25.

Kurian, V., Abdul Wahab, M. M., Kheang, T. S., and Liew, M. S., 2014. System reliability of existing jacket platform in Malaysian water (failure path and system reliability index)., 567: 307-312.

Murotsu, Y., Okada, H., Taguchi, K., Grimmelt, M., and Yonezawa, M., 1984. Automatic generation of stochastically dominant failure modes of frame structures., 2 (1): 17-25.

Pan, Q., and Dias, D., 2017. An efficient reliability method combining adaptive support vector machine and monte Carlo simulation., 67: 85-95.

Rackwitz, R., and Fiessler, B., 1978. Structural reliability under combined random load sequences., 9: 489-494.

Sadoughi, M., Li, M., and Hu, C., 2018. Multivariate system reliability analysis considering highly nonlinear and dependent safety events., 180: 189-200.

Shabakhty, N., 2011. System failure probability of offshore jack-up platforms in the combination of fatigue and fracture., 18 (1): 223-243.

Shao, S., and Murotsu, Y., 1999. Approach to failure mode analysis of large structures., 14 (1-2): 169-177.

Thoft-Christensen, P., 1990. Consequence modified-unzipping of plastic structures., 7 (2): 191-198.

Thoft-Christensen, P., and Murotsu, Y., 1986.. Springer, New York, 143-214.

Vazirizade, S. M., Nozhati, S., and Zadeh, M. A., 2017. Seismic reliability assessment of structures using Artificial Neural Network., 11: 230-235.

White, G. J., and Ayyub, B. M., 2010. Reliability methods for ship structures., 97 (4): 86-96.

March 22, 2019;

May 27, 2019;

July 22, 2019

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2020

. Tel: 0086-532-66781125

E-mail: dongsh@ouc.edu.cn

(Edited by Xie Jun)